حرکت بر خط راست – از صفر تا صد با حل مثالهای کاربردی
حرکت یکی از مهمترین موضوعهای فیزیک است. هر چیزی در جهان حرکت میکند. حتی اگر در خانه در حال استراحت باشید باز هم حرکت میکنید زیرا زمین در مدار خود به دور خورشید میچرخد. حرکت در فیزیک بدان معنا است که موقعیت جسمی با گذشت زمان تغییر میکند. به زبان ریاضی حرکت با عبارتهای جابجایی، مسافت، سرعت، تندی، شتاب و زمان توصیف میشود. در این مبحث حرکت بر خط راست را با حل مثالهای کاربردی یاد میگیریم.


حرکت بر خط راست
اگر مکان جسمی با گذشت زمان نسبت به محیط اطرافش تغییر کند، آن جسم حرکت کرده است. حرکت بر خط راست چیزی جز حرکت خطی نیست و در یکبعد اتفاق میافتد. شما پس از مطالعه این مبحث موارد زیر را به خوبی فرا خواهید گرفت.
- با تفاوت بین مسافت و جابجایی و همچنین سرعت و تندی آشنا خواهید شد.
- با تعاریف سرعت لحظهای، سرعت نسبی و سرعت متوسط آشنا میشوید.
- تفاوت بین شتاب متوسط و لحظهای را درک خواهید کرد.
- نمودارهای مکان-زمان و سرعت-زمان را برای حرکت بر خط راست یکنواخت و غیر یکنواخت به راحتی تفسیر خواهید کرد.
- معادلات حرکت با شتاب ثابت را فرا خواهید گرفت.
- حرکت تحت جاذبه زمین را به راحتی درک میکنید.
در ادامه با مفاهیمی همچون مسافت، جابجایی، تندی، سرعت و شتاب به اختصار آشنا میشویم.
مکان، جابجایی و مسافت
حرکت بر خط راست به معنای حرکت بر خط افقی یا عمودی با دو جهت چپ و راست یا بالا و پایین است. برای این نوع حرکت ابتدا نقطهای را به عنوان نقطه مرجع یا مبدأ انتخاب میکنیم.
مکان در فیزیک
اگر مسیر حرکت را خط افقی با مبدأ O در تصویر زیر در نظر بگیریم مکانهای سمت راست نقطه O مثبت و مکانهای سمت چپ این نقطه منفی خواهند بود.
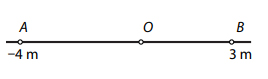
در تصویر بالا ذره B در مکان 3+ متر و ذره A در مکان 4- متر قرار گرفتهاند. مکان اجسام معمولا به صورت تابعی بر حسب زمان به صورت x(t) نوشته میشود.
جابجایی در فیزیک چیست ؟
در حرکت بر خط راست، به تغییر مکان ذره از مکانی به مکان دیگر جابجایی گفته میشود. اگر ذره از مکان به مکان برود، جابجایی آن در فاصله زمانی برابر خواهد بود. در واقع، مکان ذره برابر تغییرات جابجایی آن از مبدأ است. برای مثال حالتهای زیر را برای تصویر بالا در نظر بگیرید.
- اگر ذره از O به B حرکت کند به اندازه 3 متر جابجا شده است.
- اگر ذره از نقطه O به نقطه A برود به اندازه 4- متر جابجا میشود.
- اگر ذره از نقطه A به B حرکت کند به اندازه 7 متر جابجا شده است.
- اگر ذره از نقطه B به A برود به اندازه 7- متر جابجا شده است.
مکان و جابجایی با بردار نشان داده میشوند و از این رو بزرگی و جهت دارند. علامت بردار نشاندهنده جهت بردار و قدر مطلق آن بیانگر بزرگی بردار است.
مسافت چیست ؟
به کل مسیر پیموده شده توسط ذره، مسافت گفته میشود. به عنوان مثال، اگر در تصویر داده شده در بالا ذره از A به B و سپس به نقطه O حرکت کند جابجایی ذره برابر ۴ متر خواهد بود ولی مسافت طی شده توسط آن برابر ۱۰ متر است.
مثال 1: ذرهای در امتداد خط راست حرکت میکند. اگر مکان ذره بر حسب زمان به صورت x(t) نشان داده شود داریم.
مسافت ذره را در فاصله زمانی t=0 تا t=6 به دست آورید.
پاسخ: ذره در 3 ثانیه اول حرکتش به اندازه ۲ متر به سمت راست حرکت کرده است سپس از زمان ۳ تا ۶ ثانیه در جهت منفی محور x به اندازه 7 متر جابجا شده است. در نتیجه در مدت زمان ۶ ثانیه مسافت کل پیموده شده توسط ذره ۹ متر است.
پس از آشنایی با مفاهیم جابجایی و مسافت، در ادامه به توصیف سرعت میپردازیم.
سرعت چیست ؟
به تغییرات مسافت با زمان تندی میگویند. سرعت نیز به صورت تغییرات جابجایی بر حسب زمان تعریف میشود.
سرعت متوسط
اگر جسمی مسیر معینی را با سرعتهای متفاوتی طی کند به منظور توصیف حرکت آن، از مفهوم سرعت متوسط استفاده میشود. سرعت متوسط یک جسم را به صورت جابجایی بر واحد زمان تعریف میکنند. اگر و به ترتیب مکانهای جسمی در زمانهای و باشند، سرعت متوسط آن به صورت زیر نوشته خواهد شد.
در رابطه بالا برابر با جابجایی ذره در مدت زمان است. همچنین، تندی متوسط جسم از تقسیم کل مسافت طی شده در مدت زمان معینی به دست میآید.
اگر جهت حرکت جسم در مدت زمان حرکت تغییری نکند آنگاه سرعت متوسط و تندی متوسط مقادیر یکسانی خواهد داشت. به منظور داشتن درک عمیقتری از تفاوت سرعت و تندی متوسط به مثالهای زیر توجه کنید.
مثال اول سرعت متوسط
مکان ذرهای که بر روی محور x حرکت میکند به صورت زیر تعریف شده است.
در رابطه داده شده x بر حسب متر و t بر حسب ثانیه هستند. سرعت متوسط ذره را در فاصله زمانی ۳ تا ۴ ثانیه به دست بیاورید.
پاسخ
برای محاسبه سرعت متوسط از رابطه زیر استفاده میکنیم.
در زمان ، مکان به صورت زیر به دست خواهد آمد.
در زمان خواهیم داشت.
با جایگزینی مقادیر به دست آمده در رابطه سرعت متوسط، مقدار آن به صورت زیر به دست میآید.
مثال دوم سرعت متوسط
فردی بر روی مسیر دایرهای ۳۰۰ متری در حال دویدن است و در مدت زمان ۲۰۰ ثانیه به مکان اولیه خود بازمیگردد. سرعت و تندی متوسط این شخص را به دست بیاورید.
پاسخ
تندی متوسط به صورت زیر محاسبه میشود.
از آنجایی که دونده به مکان اولیه بازمیگردد، جابجایی کل او برابر صفر خواهد بود. از این رو، سرعت متوسط برابر صفر است.
سرعت نسبی
هنگامی که گفته میشود شخصی با سرعت به سمت جنوب حرکت میکند بدان معنا است که این شخص مسافت 10 کیلومتر را در مدت زمان یک ساعت از نقطه شروع طی خواهد کرد. بنابراین، سرعت مورد نظر نسبت به نقطه مرجعی در نظر گرفته شده است. در حقیقت، سرعت اجسام همیشه نسبت به اجسام دیگر سنجیده میشود.
سرعت نسبی جسم ۱ نسبت به سرعت نسبی جسم ۲ نرخ تغییرات مکان جسم ۱ نسبت به جسم ۲ به عنوان نقطه مرجع است. به عنوان مثال، اگر و سرعتهای دو جسم در امتداد خط راست باشند، سرعت نسبی جسم B نسبت به جسم A برابر خواهد بود.
نکته مهم در مورد سرعت نسبی
مکان و در نتیجه سرعت جسم نسبت به اجسام دیگر سنجیده میشود. اگر نقطه مرجع ساکن باشد، توصیف حرکت جسم به آسانی امکانپذیر است. ولی این سوال مطرح میشود هنگامی که جسم مرجع در حال حرکت باشد توصیف حرکت بر خط راست چگونه انجام خواهد شد. با استفاده از مفهوم حرکت نسبی میتوان به سوال مطرح شده پاسخ داد.
فرض کنید مکانهای اولیه اجسام A و B به ترتیب برابر و است. اگر جسم A در جهت مثبت محور x با سرعت و جسم B در همان جهت با سرعت حرکت کنند، مکانهای این دو جسم پس از گذشت زمان t به صورت زیر نوشته میشوند.
تصویر زیر مکانهای اولیه دو جسم A و B را نشان میدهد.
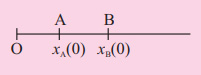
جدایی نسبی جسم B از A به صورت زیر به دست میآید.
در رابطه بالا به سرعت نسبی جسم B نسبت به جسم A میگویند. در نتیجه، با استفاده از مفهوم سرعت نسبی، مساله دو جسم به مساله یکجسمی کاهش مییابد.
مثال سرعت نسبی حرکت دو قطار
قطار A با سرعت بر روی ریل مستقیمی از شمال به سمت جنوب حرکت میکند. قطار B با سرعت از جنوب به سمت شمال در حال حرکت است. سرعت نسبی قطار B نسبت به قطار A چقدر خواهد بود.
پاسخ
با در نظر گرفتن جهت مثبت در راستای جنوب به شمال، برای قطار B خواهیم داشت.
سرعت قطار A نیز به صورت زیر نوشته میشود.
$$$$v_{A}=+\ -60 \ \frac{km}{h}$$$$
در نتیجه، سرعت قطار B نسبت به قطار A به صورت زیر محاسبه خواهد شد.
همانگونه که در مثال بالا مشاهده میکنید سرعت نسبی یک قطار نسبت به قطار دیگر به صورت جمع سرعتهای دو قطار به دست آمد. از این رو، هنگامی که در قطاری نشستهاید و قطار دیگری در جهت مخالف از کنار شما میگذرد حرکت آن را بسیار سریع تصور میکنید.
در اغلب موارد، زمین بهترین مرجع برای حل مسائل فیزیکی است. با این حال، گاهی وقتها محاسبه سرعت جسم نسبت به چارچوبهای مختلف آسانتر خواهد بود. تصور کنید در مسابقات قایقرانی شرکت کردهاید و به سمت پایین رودخانه در حال حرکت هستید. دانستن سرعت شما نه تنها نسبت به جریان آب رودخانه بلکه نسبت به خشکی نیز مهم خواهد بود. حتی دانستن سرعت حرکت شما نسبت به رقیبتان مهم است.

در برخورد با این مسئلهها، سرعت جسم نسبت به چارچوب مرجع آن تعیین میشود. به عنوان مثال، سرعت جسم A نسبت به چارچوب مرجع C به صورت نوشته میشود. حتی اگر سرعت جسم A نسبت به C را ندانید، با یافتن سرعت جسم A نسبت به جسم واسطهای مانند B و سرعت جسم B نسبت به C، با استفاده از جمع برداری میتوانید سرعت جسم A نسبت به C را به صورت زیر به دست بیاورید.
به منظور درک بهتر مفهوم سرعت نسبی در حرکت بر خط راست به حل مثالی در این زمینه میپردازیم.
مثال سرعت نسبی هواپیما نسبت به زمین
هواپیمایی با سرعت نسبت به باد به سمت شرق پرواز میکند. باد با سرعت نسبت به زمین در جهت شمال میوزد. سرعت هواپیما را نسبت به زمین به دست بیاورید.

پاسخ
سرعت هواپیما نسبت به باد و سرعت باد نسبت به زمین به ترتیب با و نشان داده میشوند. ذکر این نکته مهم است که این دو سرعت، بردارهای دوبعدی هستند. سرعت هواپیما نسبت به زمین، ، به صورت زیر نوشته میشود.
جمع برداری فوق در تصویر زیر نشان داده شده است.
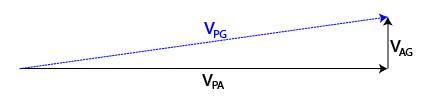
بزرگی سرعت هواپیما نسبت به زمین به آسانی با استفاده از قضیه فیثاغورث به دست میآید.
زاویه هواپیما به صورت زیر به دست خواهد آمد.
بنابراین هواپیما با سرعت نسبت به زمین با زاویه در جهت شمال شرق پرواز میکند.
شتاب در حرکت بر خط راست
آیا تاکنون به این سوال فکر کردهاید که اگر سرعت اجسام و هر آنچه که در اطراف ما است هیچگاه تغییر نمیکرد چه اتفاقی رخ میداد. اجسام ساکن همیشه در حال سکون باقی میماندند و اجسام در حال حرکت به حرکت خود با سرعت ثابت و بدون تغییر جهت ادامه میدادند. اما در واقع اینگونه نیست و سرعت اجسام به طور پیوسته در حال تغییر است. به طور مثال، هنگامی که در اتوبوس یا قطار نشستهاید متوجه خواهید شد که گاهی سرعت حرکت زیاد و گاهی کم میشود. در واقع، سرعت شما با زمان تغییر کرده است. به تغییرات سرعت بر حسب زمان شتاب میگویند.
مثال شتاب در حرکت بر خط راست
رانندهای که به سمت شرق حرکت میکند، سرعت ماشین را در مدت زمان ۳ ثانیه از مقدار 0 به افزایش میدهد. مقدار شتاب متوسط را دست آورید.
پاسخ
مقادیر سرعت اولیه و نهایی و زمان به صورت زیر داده شده است.
با جایگذاری مقادیر داده شده در معادله سرعت متوسط، خواهیم داشت:
در نتیجه مقدار شتاب متوسط خواهد بود.
ذکر این نکته مهم است که به شتاب جسم در هر لحظه شتاب لحظهای گفته میشود و از مشتق سرعت بر حسب زمان به دست خواهد آمد.
نمودار مکان زمان در حرکت بر خط راست
اگر جسمی را به حرکت درآورید متوجه خواهید شد که جسم در زمانهای متفاوت در مکانهای مختلفی خواهد بود. مکانهای متفاوت و زمانهای متناظر با آنها را میتوان به صورت نموداری رسم کرد. به این نمودار، نمودار مکان زمان میگویند. زمان در امتداد محور افقی و مکان جسم در امتداد محور عمودی نشان داده میشوند.
جسمی را تصور کنید که در فاصله ۲۰ متری از مبدأ در حالت سکون قرار دارد. همانطور که در تصویر زیر میبینید نمودار مکان این جسم بر حسب زمان به صورت خط مستقیمی موازی محور افقی رسم شده است.
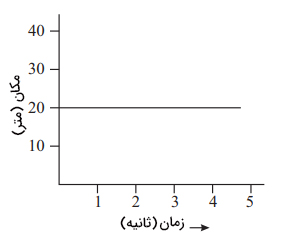
نکته: در نمودار مکان زمان محور افقی با t و محور عمودی با x نشان داده میشوند.
نموار مکان زمان در حرکت یکنواخت
اکنون حالتی را در نظر بگیرید که جسمی مسافتهای مساوی را در زمانهای یکسان طی میکند. به عنوان مثال، اگر جسم هر ثانیه به اندازه ده متر در مدت زمان ۵ ثانیه جابجا شود، موقعیت مکانی جسم در زمانهای متفاوت در جدول زیر نشان داده شده است.

نمودار مکان زمان جسم به صورت زیر رسم میشود.
همانگونه که در تصویر بالا دیده میشود نمودار، خط مستقیمی با شیب مثبت است. به حرکتی که در آن جسم با سرعت ثابتی حرکت میکند، حرکت یکنواخت میگویند. در حرکت یکنواخت، نمودار مکان زمان خط مستقیم با شیب ثابت خواهد بود.
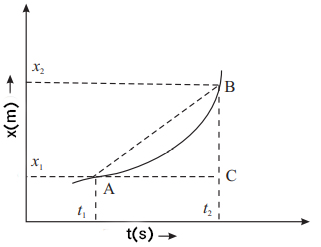
نمودار مکان زمان در حرکت غیر یکنواخت
قطاری را در نظر بگیرید که از ایستگاه اول شروع به حرکت میکند و با افزایش سرعت به اندازهای معین، برای مدت زمان مشخصی با سرعت ثابت حرکت میکند. سپس، راننده قطار به هنگام نزدیک شدن به ایستگاه بعدی سرعت را کاهش میدهد. اگر شما مسافر این قطار باشید متوجه خواهید شد که قطار در فاصلههای زمانی یکسان مسافتهای یکسانی را طی نکرده است. به این حرکت، حرکت غیر یکنواخت گفته میشود.
نموار مکان زمان جسمی با حرکت غیر یکنواخت به صورت زیر نشان داده شده است. در این نمودار، فاصله جسم از مبدأ با گذشت زمان افزایش مییابد.
تفسیر نمودار مکان زمان
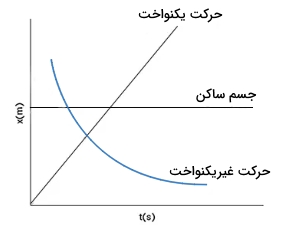
برای اجسام متحرک، نمودارهای مکان زمان متفاوتی وجود دارند. ولی در حالت کلی نمودارها به سه دسته زیر تقسیم میشوند.
- اگر نمودار خط مستقیمی موازی محور افقی باشد آنگاه جسم در حالت سکون قرار دارد.
- اگر نمودار خط مستقیمی با زاویه با محور افقی (محور زمان) باشد آنگاه جسم به صورت یکنواخت حرکت میکند.
- نمودار غیرخطی نشاندهنده حرکت با سرعت غیر یکنواخت خواهد بود.
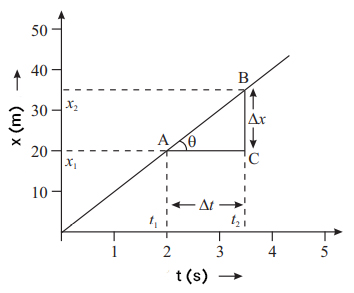
محاسبه سرعت با استفاده از نمودار مکان زمان در حرکت یکنواخت
اگر نمودار مکان زمان خط مستقیم باشد، شیب آن برابر با سرعت متوسط جسم متحرک خواهد بود. مطابق تصویر زیر دو نقطه به نامهای P و Q را بر روی نمودار انتخاب میکنیم. با رسم خطوط موازی محورهای افقی و عمودی مثلث قائمالزاویهای را رسم میکنیم.
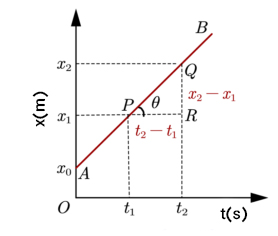
پس از رسم مثلث، سرعت متوسط به صورت زیر به دست خواهد آمد.
بنابراین، سرعت متوسط جسم برابر با شیب خط مستقیم PQ خواهد بود.
مثال نمودار مکان زمان
نمودارهای مکان زمان دو جسم A و B در تصویر زیر نشان داده شدهاند. کدام جسم با سرعت بزرگتری حرکت میکند؟
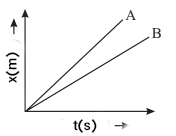
پاسخ
نمودار جسم A نسبت به نمودار جسم B شیب بیشتری دارد و در نتیجه با سرعت بیشتری حرکت میکند.
سرعت لحظهای
همانگونه که در مطالب بالاتر گفته شد جسمی که دارای حرکت یکنواخت بر خط راست است در هر لحظه دارای سرعت ثابتی خواهد بود. اما در حالت حرکت غیر یکنواخت، نمودار مکان زمان، منحنی است. در نتیجه، اندازه شیب یا سرعت متوسط بستگی به فاصلههای زمانی انتخاب شده خواهد داشت. به سرعت ذره در هر زمان یا در هر نقطه از مسیر حرکتش، سرعت لحظهای میگویند.
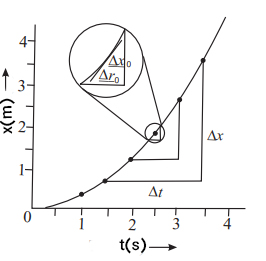
به این نکته دقت کنید که که سرعت متوسط در فاصله زمانی به صورت به دست خواهد آمد. با کوچکتر کردن فاصله زمانی و بردن آن به سمت صفر، سرعت متوسط با سرعت لحظهای برابر میشود.
نکته: در حرکت یکنواخت سرعت متوسط با سرعت لحظهای برابر است.
مثال سرعت لحظهای
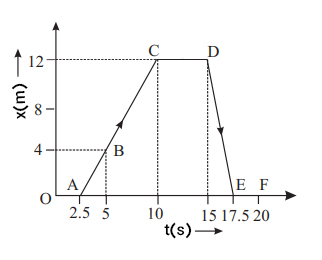
نمودار مکان زمان جسمی برای مدت زمان ۲۰ ثانیه در تصویر زیر نشان داده شده است. در فاصلههای زمانی زیر مسافت طی شده توسط جسم و سرعت آن را به دست آورید. همچنین سرعت متوسط را برای کل حرکت حساب کنید.
- 0 تا 5 ثانیه
- ۵ تا ۱۰ ثانیه
- ۱۰ تا ۱۵ ثانیه
- ۱۵ تا ۱۷/۵ ثانیه
پاسخ
در مدت زمان 0 تا ۵ ثانیه، جسم به اندازه ۴ متر حرکت کرده است. سرعت آن در این فاصله زمانی به صورت زیر به دست میآید.
برای فاصله زمانی 5 تا ۱۰ ثانیه جسم به اندازه 8=4-12 متر جابجا شده است. سرعت جسم در این بازه زمانی برابر است با
در مدت زمان 10 تا ۱۵ ثانیه، به دلیل آنکه نمودار حرکت جسم یک خط مستقیم موازی محور افقی یعنی زمان است، جابجایی جسم و در نتیجه سرعت آن نیز برابر صفر خواهد بود.
در پایان، برای فاصله زمانی 15 تا ۱۷/۵ ثانیه جسم به مکان اولیه خود بازگشته و به اندازه ۱۲ متر جابجا شده است.
همانگونه که میبینیم در مدت زمان 15 تا 17/5 ثانیه نمودار مکان زمان خطی با شیب منفی است. بنابراین، مقدار سرعت در این فاصله زمانی منفی خواهد بود.
نمودار سرعت زمان در حرکت بر خط راست
همانند نمودار مکان زمان، میتوان سرعت را نیز بر حسب زمان رسم کرد.
نموار سرعت زمان در حرکت یکنواخت
همانطور که در مطالب بالا توضیح داده شد در حرکت یکنواخت سرعت حرکت جسم بر حسب زمان ثابت است. نمودار سرعت بر حسب زمان برای چنین حرکتی خط مستقیمی موازی محور افقی خواهد بود.
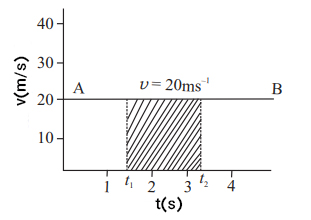
نموار سرعت زمان در حرکت غیر یکنواخت
اگر سرعت جسمی به صورت یکنواخت بر حسب زمان تغییر کند، شتاب جسم ثابت خواهد بود. نمودار سرعت بر حسب زمان چنین حرکتی خط مستقیمی است که با محور افقی زاویه میسازد (خط AB در نمودار نشان داده شده در تصویر).
شتاب متوسط جسم به صورت زیر به دست میآید.
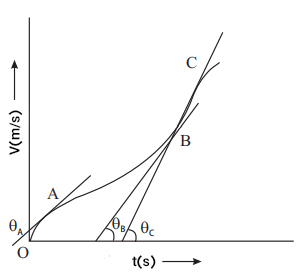
از رابطه بالا مشخص است که شتاب برابر شیب خط AB است. از آنجایی که شیب خط AB ثابت است در نتیجه شتاب متوسط جسم نیز ثابت خواهد بود. هنگامیکه نرخ تغییرات سرعت جسمی ثابت نباشد جسم دارای حرکت با شتاب غیر یکنواخت است. در این حالت شیب نمودار سرعت ــ زمان در هر لحظه تغییر میکند. به عنوان مثال، همانگونه که در تصویر زیر دیده میشود زاویههای در نقاط A و B و C متفاوت هستند.
تفسیر نمودار سرعت زمان
با استفاده از نمودار v-t میتوانیم جابجایی پیموده شده توسط جسم و شتاب آن را در لحظههای مختلف به دست بیاوریم.
تعیین مسافت طی شده توسط جسم
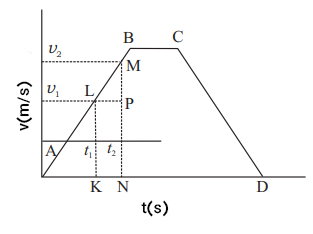
نمودار سرعت بر حسب زمان در تصویر زیر را در نظر بگیرید. بخش AB حرکت با شتاب ثابت را نشان میدهد. قسمت BC نمودار نشاندهنده حرکت یکنواخت با شتاب صفر است.
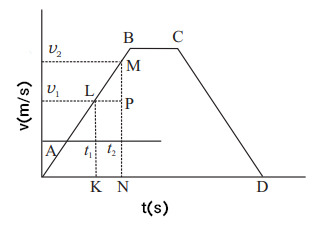
در حرکت یکنواخت، مسافت طی شده توسط جسم در فاصله زمانی و برابر خواهد بود. این عبارت برابر مساحت زیر نمودار سرعت بر حسب زمان در فاصله زمانی و خواهد بود.
مساحت ذوزنقه KLMN = مسافت
تعیین شتاب جسم
میدانیم که شتاب جسم نرخ تغییرات سرعت بر حسب زمان است. با توجه به تصویر نشان داده شده در ادامه، شتاب متوسط برابر با شیب وتر AB خواهد بود.
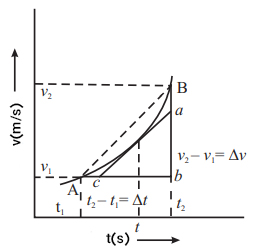
اگر فاصله زمانی به سمت صفر میل کند، شتاب متوسط برابر با شتاب لحظهای خواهد شد. بنابراین، شتاب لحظهای به صورت زیر به دست میآید.
عبارت بالا برابر با شیب خط مماس در نقطه t است (). بنابراین، شیب خط مماس بر نمودار سرعت-زمان در یک نقطه، شتاب حرکت را در آن لحظه به ما میدهد.
مثال نمودار سرعت زمان
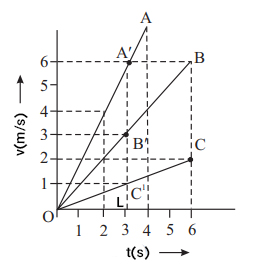
نمودارهای سرعت زمان برای سه جسم A و B و C در تصویر زیر نشان داده شدهاند.
- کدام جسم دارای سرعت بیشینه است؟ مقدار آن را به دست آورید.
- مسافت طی شده توسط این سه جسم را در ۳ ثانیه اول حرکت به دست آورید.
- کدام یک از این سه جسم در انتهای مسیر، بیشترین مسافت را طی کردهاند.
- سرعتهای اجسام در زمان ۲ ثانیه چقدر است؟
پاسخ
۱. از آنجایی که نمودار سرعت زمان جسم A با محور افقی (زمان) بیشترین زاویه را میسازد، در نتیجه شیب آن نسبت به دو نمودار اجسام B و C بیشتر است. بنابراین شیب جسم A بیشینه است و مقدار آن از رابطه زیر محاسبه میشود.
2. مسافت طی شده توسط جسم برابر با مساحت زیر نمودار سرعت-زمان در فاصله زمانی t است. در نتیجه مسافت طی شده توسط سه جسم داده شده در مدت زمان ۳ ثانیه به صورت زیر به دست میآید.
مساحت OA'L = مسافت طی شده توسط جسم A
مساحت OB'L = مسافت طی شده توسط جسم B
مساحت OC'L = مسافت طی شده توسط جسم B
3. در انتهای مسیر، جسم B بیشترین مسافت را پیموده است.
4. از آنجایی که نمودار سرعت زمان برای هر سه جسم خط مستقیم است، شتاب لحظهای با شتاب متوسط برابر خواهد بود. در زمان ۲ ثانیه سرعت جسم A برابر و سرعت جسم B برابر و سرعت جسم C در حدود به دست خواهند آمد.
معادلات حرکت بر خط راست
همانطور که در مباحث بالا یاد گرفتیم برای توصیف حرکت جسمی بر خط راست از مفاهیم فیزیکی مانند مسافت، سرعت و شتاب استفاده میکنیم. در حرکت با شتاب ثابت، سرعت جسم و مسافت طی شده توسط آن با استفاده معادلات حرکت محاسبه میشوند.
معادله حرکت یکنواخت
به منظور محاسبه معادلات حرکت فرض میکنیم که زمان اولیه، ، برابر صفر است. بنابراین میتوانیم زمان را برابر t بگیریم. برای این حالت مکان اولیه () و سرعت اولیه () را به ترتیب برابر و قرار میدهیم. همچنین مکان و سرعت در زمان t برابر x و v خواهند بود. در نتیجه سرعت متوسط به صورت زیر به دست میآید.
اولین معادله حرکت با شتاب یکنواخت
با استفاده از اولین معادله حرکت با شتاب یکنواخت میتوان سرعت جسم را بعد از گذشت زمان معین به دست آورد.
با استفاده از فرضهای گفته شده در بخش حرکت یکنواخت، معادله بالا به صورت زیر نوشته خواهد شد.
مثال اول حرکت با شتاب یکنواخت
اتومبیلی از حال سکون با شتاب شروع به حرکت میکند. سرعت این اتومبیل را بعد از گذشت ۵ ثانیه به دست آورید.
پاسخ
دادههای مساله به صورت زیر است.
با استفاده از اولین معادله به دست آمده برای حرکت بر خط راست، سرعت حرکت اتومبیل به صورت زیر به دست خواهد آمد.
دومین معادله حرکت با شتاب یکنواخت
مکان جسم پس از گذشت زمان t با استفاده از دومین معادله حرکت با شتاب یکنواخت به دست خواهد آمد. ابتدا فرضهای زیر را در نظر بگیرید.
مسافت طی شده توسط جسم برابر با مساحت زیر نمودار خواهد بود.
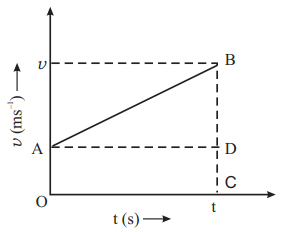
مساحت زیر نمودار نشان داده در تصویر بالا به صورت زیر به دست میآید.
با جایگزینی رابطه در رابطه بالا خواهیم داشت.
مثال دوم حرکت با شتاب یکنواخت
اتومبیل A در جاده مستقیمی با سرعت یکنواخت در حال حرکت است. اتومبیل B با سرعت یکنواخت به دنبال اتومبیل A در حرکت است. هنگامی که فاصله آنها به 2/5 کیلومتر میرسد، اتومبیل B با شتاب 20 متر بر مجذور ثانیه سرعت خود را کاهش میهد. در چه فاصله و زمانی اتومبیل B از اتومبیل A سبقت خواهد گرفت؟
پاسخ
فرض کنید اتومبیل B در فاصله x و پس از گذشت زمان t از اتومبیل A سبقت میگیرد. بنابراین، اتومبیل A در مدت زمان t مسافت را طی خواهد کرد. اتومبیل B در همین زمان مسافت را به صورت زیر طی میکند.
طبق صورت مساله فاصله بین دو اتومبیل برابر 2/5 کیلومتر است. در نتیجه زمان به صورت زیر به دست میآید.
در نتیجه با حل معادله درجه ۲ به دست آمده زمان t برابر نیم ساعت به دست خواهد آمد.
سومین معادله حرکت با شتاب یکنواخت
سومین معادله حرکت با شتاب ثابت هنگامی استفاده میشود که مکان، شتاب و سرعت اولیه جسم داده شده باشند.
همچنین از اولین معادله حرکت با شتاب ثابت داریم.
با جایگزین کردن معادله فوق در معادله مکان خواهیم داشت.
در نتیجه سه معادله به دست آمده برای حرکت با شتاب ثابت به صورت زیر نوشته میشوند.
مثال سوم حرکت با شتاب یکنواخت
موتورسیکلتی در امتداد جاده مستقیمی با شتاب ثابت حرکت میکند. اگر مکان و سرعت اولیه موتورسیکلت به ترتیب برابر 5m و باشند، مطلوب است،
- مکان و سرعت موتورسیکلت در زمان t=2s و
- مکان موتورسیکلت هنگامیکه سرعت آن برابر با است.
پاسخ
دادههای مساله به صورت زیر است.
حل قسمت ۱: با استفاده از معادله دوم حرکت با شتاب ثابت خواهیم داشت.
به منظور محاسبه سرعت از معادله اول حرکت با شتاب ثابت استفاده میکنیم.
حل قسمت ۲: برای محاسبه مکان موتورسیکلت از معادله سوم حرکت با شتاب ثابت استفاده میکنیم.
حرکت تحت جاذبه زمین
هنگامیکه توپی را به بالا پرتاب میکنیم یا سنگی را از ارتفاع معینی به پایین میاندازیم هر دو به سمت زمین باز خواهند گشت. آیا میدانید چه عاملی سبب بازگشت آنها به سمت زمین است؟ پاسخ نیروی جاذبه زمین است. نیروی جاذبه در جهت عمود بر اجسام وارد میشود. بنابراین، حرکت تحت جاذبه زمین در امتداد خط مستقیم و یکبعدی خواهد بود.
- نکته 1: سقوط آزاد جسم به سمت زمین یکی از رایجترین مثالهای حرکت با شتاب ثابت است.
- نکته 2: در غیاب مقاومت هوا، همه اجسام با هر اندازه و وزنی با شتاب یکسانی سقوط خواهند کرد.
- نکته ۳: شتاب جاذبه با ارتفاع تغییر میکند. اما برای فاصلههای کوچک در برابر شعاع زمین مقدار آن ثابت در نظر گرفته میشود.
شتاب جسمی که تحت جاذبه زمین سقوط آزاد میکند با g نشان داده میشود. بر روی سطح زمین یا در نزدیکی آن مقدار g برابر است.
مثال سقوط آزاد
سنگی از ارتفاع 50 متری رها میشود. مقدارهای زیر را به دست آورید.
- مسافتی که جسم در مدت زمان ۲ ثانیه طی میکند.
- سرعت سنگ هنگامی که به زمین میرسد.
- سرعت سنگ ۳ ثانیه پس از رها شدن چقدر خواهد بود.
پاسخ
چون سنگ از ارتفاع 50 متری رها میشود در نتیجه سرعت اولیه آن برابر صفر است. همچنین مبدأ را نقطه شروع حرکت سنگ در نظر میگیریم.
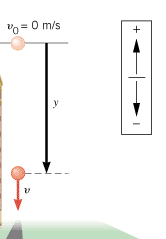
همانگونه که در تصویر بالا دیده میشود محور y زیر مبدأ منفی خواهد بود. مقدار شتاب نیز به دلیل آنکه جهتش به سمت پایین و در جهت منفی محور y است منفی میشود.
قسمت ۱: از معادله دوم حرکت با شتاب ثابت، مسافت طی شده توسط سنگ در مدت زمان ۲ ثانیه به صورت زیر به دست میآید.
علامت منفی y نشان میدهد که فاصله طی شده زیر مبدأ و به سمت پایین است.
قسمت ۲: بر روی زمین خواهد بود. با استفاده از معادله سوم حرکت با شتاب ثابت خواهیم داشت.
قسمت ۳: با استفاده از معادله اول حرکت با شتاب ثابت، ، در زمان ۳ ثانیه داریم.
مقدار به دست آمده برای سرعت نشان میدهد که جهت آن در زمان ۳ ثانیه به سمت پایین خواهد بود.
معادلات حرکت بر خط راست
جدول زیر معادلههای حرکت و موارد استفاده هر کدام را نشان میدهد. در حرکت بر خط راست با شتاب ثابت باید به دو نکته زیر توجه کرد.
- هنگامی که شتاب در جهت حرکت جسم باشد مقدار آن مثبت خواهد بود.
- هنگامی که شتاب و جهت حرکت جسم در دو راستای مخالف باشند، مقدار شتاب منفی است.
| جابجایی | |
| جابجایی کل | |
| سرعت متوسط | |
| سرعت لحظهای | |
| تندی متوسط | |
| تندی لحظهای | |
| شتاب متوسط | |
| شتاب لحظهای | |
| محاسبه مکان با استفاده از سرعت متوسط | |
| سرعت متوسط | |
| محاسبه سرعت با استفاده از شتاب (شتاب ثابت) | |
| محاسبه مکان با استفاده از سرعت و شتاب (شتاب ثابت) | |
| محاسبه سرعت با استفاده از مکان (شتاب ثابت) | |
| سرعت در سقوط آزاد | |
| ارتفاع سقوط آزاد | |
| محاسبه سرعت با استفاده از ارتفاع در حرکت سقوط آزاد | |
| محاسبه سرعت با استفاده از شتاب | |
| محاسبه مکان با استفاده از سرعت |
حل مثالهای کاربردی بیشتر
در ادامه به حل چند مثال میپردازیم.
مثال ۱
در جاده دوطرفه، ماشین A با سرعت در حال حرکت است. ماشینهای B و C با سرعت در جهت مخالف یکدیگر به ماشین A نزدیک میشوند. در یک لحظه، هنگامی که فاصله AB با AC با هم مساوی و برابر یک کیلومتر میشود، راننده B تصمیم میگیرد قبل از راننده C از A سبقت بگیرد. کمینه شتابی که که راننده B نیاز دارد تا از تصادف جلوگیری کند چه مقدار است؟
پاسخ
تصور کنید ماشین A به سمت شرق در حرکت است. بنابراین، ماشین B درحالیکه به سمت شرق در حرکت است از پشت به ماشین A نزدیک میشود. همچنین، ماشین C درحالیکه به سمت غرب در حال حرکت است از روبرو به ماشین A در حال نزدیک شدن است. برای حل مساله داده شده حرکت به سمت شرق را مثبت و حرکت به سمت غرب را منفی در نظر میگیریم.
برای حل مساله ابتدا سرعتهای ۳ ماشین را به m/s تبدیل میکنیم.
اکنون سرعت نسبی B را نسبت به A و سرعت نسبی C را نسبت به A به صورت زیر به دست میآوریم.
فرض کنید ماشین B با شتاب سعی در گرفتن سبقت از A دارد. بنابراین شتاب نسبی B نسبت به A به صورت زیر به دست خواهد آمد.
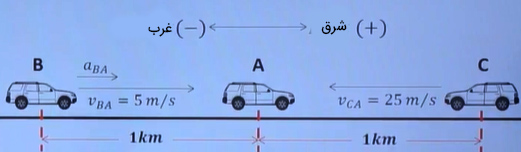
به منظور جلوگیری از تصادف، B باید قبل از C به ماشین A برسد. مدت زمانی که C به A میرسد برابر است با
B نیز در مدت زمان ۴۰ ثانیه به ماشین A خواهد رسید. در نتیجه با در نظر گرفتن ماشین A به عنوان چارچوب مرجع و مشاهدهگر، کمینه شتابی که B نیاز دارد تا از تصادف جلوگیری کند به صورت زیر محاسبه میشود.
مقدار شتاب B مقدار به دست خواهد آمد.
مثال 2
اگر مکان جسمی بر حسب زمان به صورت زیر باشد.
سرعت جسم را در زمان t=1s به دست آورید.
پاسخ
همانگونه که در توضیحات بالا اشاره شد مشتق مکان جسم بر حسب زمان سرعت حرکت جسم را خواهد داد.
در نتیجه در زمان t=1s سرعت حرکت جسم برابر خواهد بود.
مثال 3
توپ از سطح زمین با سرعت اولیه به طور عمودی به سمت بالا پرتاب میشود مطلوب است.
- بیشینه ارتفاعی که جسم بالا میرود.
- مدت زمانی که جسم صعود میکند.
- کل زمان پرتاب.
پاسخ
مسیر حرکت توپ از هنگام پرتاب تا هنگام رسیدن به سطح زمین در تصویر زیر نشان داده شده است.
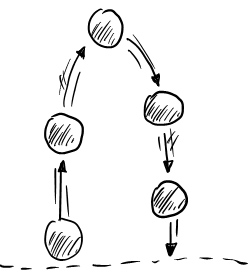
جسم با سرعت از سطح زمین به سمت بالا پرتاب میشود و پس از رسیدن به ارتفاع h، سرعت آن صفر میشود و به سمت پایین تغییر مسیر میدهد. در نتیجه مدت زمان صعود جسم تا رسیدن آن به سرعت صفر و تغییر مسیر به صورت زیر به دست خواهد آمد.
همچنین با نادیده گرفتن مقاومت هوا مدت زمان صعود و سقوط برابر خواهند بود. بنابراین، مدت زمان پرتاب برابر با است. بیشینه ارتفاعی که توپ صعود خواهد کرد نیز برابر با به دست خواهد آمد.
فیلم آموزش فیزیک پایه ۱
مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک پایه 1 برای دانشآموزان پایه دوازدهم و دانشجویان ترم اول علوم پایه و فنی مهندسی کرده است. این مجموعه آموزشی از سیزده درس تشکیل شده است که برای آشنایی بیشتر با مباحث حرکت و حل مسئله، درسهای دوم تا پنجم مفید هستند.
پس از آشنایی با کمیتهای فیزیکی و تحلیل ابعادی در درس یکم، با مفاهیم برداری و ضرب و جمع بردارها در درس دوم آشنا خواهید شد. درسهای سوم و چهارم به حرکت بر روی خط راست اختصاص دارند و میتوان در این درسها مباحث مربوط به مسافت، جابجایی، تندی، و سرعت را با جزییات بیشتری فرا گرفت.
- برای دیدن فیلم آموزش فیزیک پایه 1 + اینجا را کلیک کنید.
سقوط آزاد تحث تاثیر مقاومت هوا
به منظور توصیف حرکت جسم باید سه گام زیر را در نظر بگیریم.
- نیروهای وارد شده بر جسم را پیدا کنیم.
- با استفاده از قوانین نیوتن شتاب را به دست آوریم.
- با استفاده از تعریف شتاب و مکان اولیه و سرعت نوع حرکت را به دست آوریم.
نیروی مقاومت هوا در سرعتهای کم متناسب با سرعت حرکت جسم است و به صورت زیر نوشته میشود.
معادله بالا بدان معنا است که هر چه جسم سریعتر حرکت کند نیروی مقاومت باد بزرگتر خواهد بود. هنگامیکه دست خود را از اتومبیلی در حال حرکتی با سرعت زیاد بیرون میآورید نیروی مقاومت هوا را حس خواهید کرد. کمیت b به اندازه و شکل جسم و ویژگیهای محیط در برگیرنده شاره بستگی دارد. به کمیت b ضریب مقاومت هوا گفته میشود.
تصویر زیر جسمی را در حال سقوط نشان میدهد.
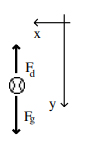
با استفاده از قانون دوم نیوتن و توجه به جهت مثبت حرکت خواهیم داشت.
از آنجایی که مقاومت هوا با افزایش سرعت جسم سقوط کننده افزایش مییابد، بنابراین نیروهای وارد شده بر جسم با یکدیگر برابر خواهند بود و جسم با سرعت ثابتی به نام سرعت حد، سقوط خواهد کرد.
معادلات حرکت
اکنون معادلات حرکت جسمی را که تحت تاثیر مقاومت هوا سقوط میکند به دست میآوریم. با جایگزینی رابطه به دست آمده برای سرعت حد در معادله به دست آمده از قانون دوم نیوتن داریم.
با استفاده از تعریف شتاب داریم.
معادله دیفرانسیل به دست آمده برای سرعت را به صورت زیر حل میکنیم.
با انتگرالگیری از طرفین رابطه بالا خواهیم داشت.
سرعت جسم بر حسب زمان به صورت زیر به دست خواهد آمد.
مثال سقوط آزاد تحت تاثیر مقاومت هوا
قطره بارانی با وزن 3/00 گرم از ارتفاع 2000 متری با سرعت حد سقوط میکند. مدت زمان (۱) رسیدن به سرعت حد و (۲) رسیدن قطره به زمین را به دست بیاورید.
پاسخ
(۱) با توجه به معادله به دست آمده برای سرعت
مدت زمان رسیدن به سرعت حد بینهایت میشود. بنابراین صورت سوال باید به این صورت اصلاح شود.
مدت زمان رسیدن سرعت قطره به 99٪ سرعت حد را به درست آورید.
با گرفتن لگاریتم از طرفین معادله بالا خواهیم داشت.
(۲) از آنجایی که قطره باران تنها در حدود ۴ ثانیه به سرعت حد میرسد، در کل مدت سقوط با این سرعت حرکت خواهد کرد. بنابراین، با این فرض که قطره با سرعت ثابت حرکت خواهد کرد داریم.
معادله مکان به عنوات تابعی از زمان به صورت زیر به دست خواهد آمد.
با حل انتگرال دو طرف تساوی خواهیم داشت.












