جمع اعداد مخلوط – به زبان ساده + حل تمرین و مثال
در آموزشهای پیشین مجله فرادرس، با اعداد مخلوط آشنا شدیم. در این آموزش از مجموعه مطالب ریاضی مجله فرادرس، ضمن مروری کوتاه بر اعداد مخلوط، درباره جمع اعداد مخلوط بحث میکنیم و مثالهایی را بررسی خواهیم.
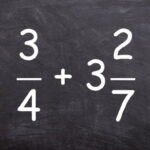
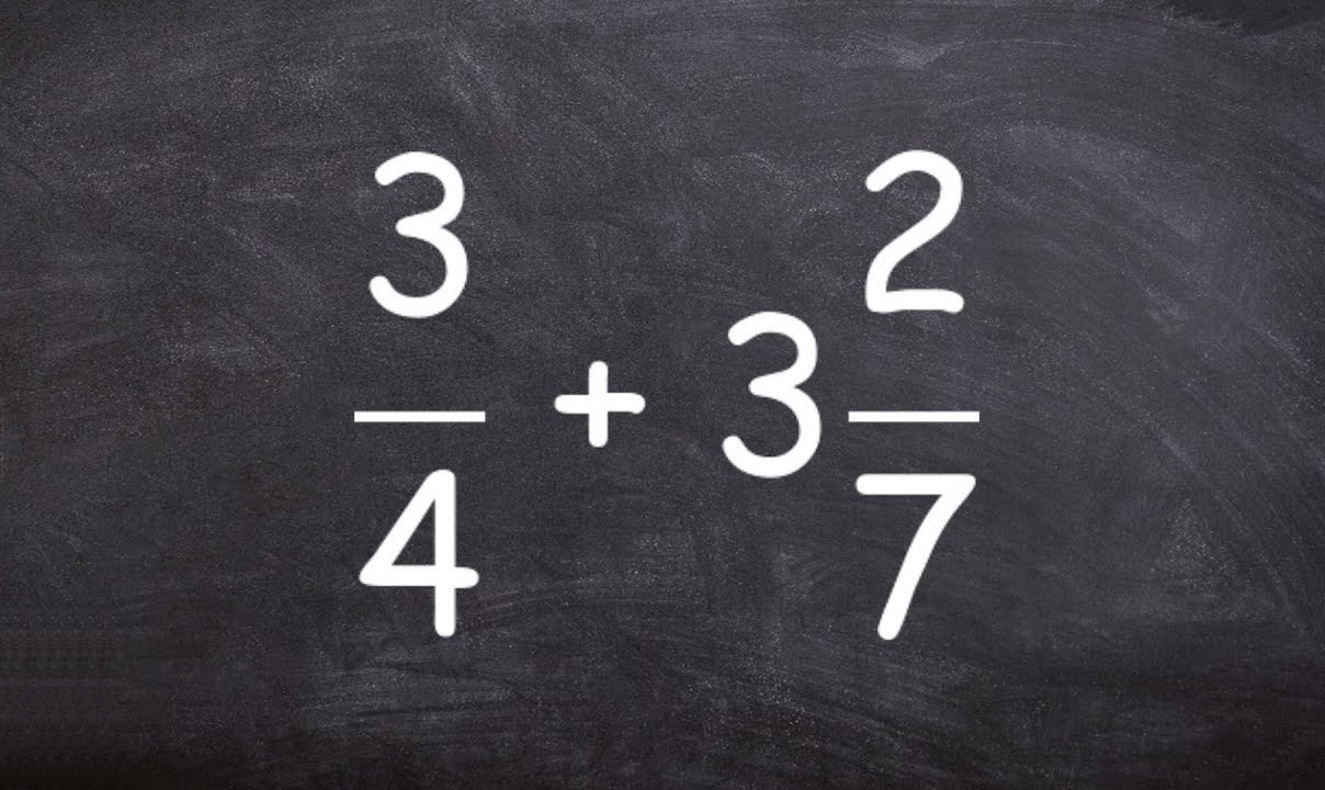
عدد مخلوط چیست؟
همانطور که در آموزشهای قبلی گفتیم، عدد مخلوط یا عدد آمیخته عددی است که از یک عدد صحیح و یک کسر (که صورت آن از مخرجش کوچکتر است) تشکیل شده است. اعداد زیر عدد مخلوط هستند:
جمع اعداد مخلوط با مخرج برابر
جمع اعداد مخلوط با مخرج برابر بهسادگی قابل انجام است. با دو روش میتوان این کار را انجام داد.
- جمع بخش صحیح بهصورت جدا و بخش کسری بهصورت جدا
- تبدیل اعداد مخلوط به اعداد کسری و جمع آنها
روش اول جمع اعداد مخلوط با مخرج برابر
در روش اول، ابتدا دو عدد صحیح را با هم جمع میکنیم، سپس کسرها را با هم جمع میزنیم.
برای مثال، فرض کنید میخواهیم دو عدد زیر را با هم جمع کنیم:
برای این کار، ابتدا دو عدد صحیح را با هم جمع میکنیم:
سپس کسرها را با هم جمع میکنیم:
در نهایت، دو عدد را جمع میکنیم:
روش دوم جمع اعداد مخلوط با مخرج برابر
در این روش، ابتدا اعداد مخلوط را به کسر تبدیل میکنیم، سپس بهسادگی، آن دو کسر را جمع میکنیم. در نهایت، عدد کسری حاصل را به عدد مخلوط تبدیل میکنیم.
برای مثال، فرض کنید میخواهیم جمع دو عدد زیر را انجام دهیم:
عدد نخست یک عدد مخلوط است که باید آن را به یک عدد کسری تبدیل کنیم. عدد دوم خودش یک کسر است و نیازی به تبدیل ندارد. عدد دوم را اینگونه مینویسیم:
بنابراین، باید جمع زیر را محاسبه کنیم:
که حاصل آن برابر است با
در گام نهایی، عدد کسری حاصل را به عدد مخلوط تبدیل میکنیم:
جمع اعداد مخلوط با مخرج نابرابر
وقتی مخرجها برابر نباشد، باید از مخرج مشترک کمک بگیریم. در این حالت نیز، میتوانیم با دو روش جمع اعداد مخلوط را انجام دهیم.
روش اول جمع اعداد مخلوط با مخرج نابرابر
در روش اول جمع اعداد مخلوط ابتدا اعداد صحیح آنها را جدا با هم جمع میکنیم، سپس کسرهایشان را با هم جمع میکنیم و حاصل را با آن جمع میبندیم. چون در این حالت، مخرجها با یکدیگر برابر نیست، باید از آنها مخرج مشترک بگیریم و سپس جمعشان کنیم. با یک مثال، جمع اعداد مختلط با مخرج نابرابر را توضیح میدهیم.
فرض کنید میخواهیم جمع زیر را انجام دهیم:
طبق آنچه گفتیم، ابتدا دو عدد صحیح را جمع میکنیم:
اکنون نوبت کسرهاست که آنها را با هم جمع کنیم:
چون که مخرج کسرها یکسان نیست، باید مخرج مشترک بگیریم و آنها را جمع کنیم. کوچکترین مضرب مشترک دو عدد و ، عدد است که میشود مخرج مشترک دو کسر. پس، جمع دو کسر بهشکل زیر انجام میشود:
اکنون هم جمع دو عدد صحیح را داریم و هم حاصلجمع دو کسر را. بنابراین، جواب نهایی جمع دو عدد مخلوط بهشکل زیر است:
میتوانیم عدد مخلوط جواب را به یک عدد کسری تبدیل کنیم:
برای آشنایی با مخرج مشترک، پیشنهاد میکنیم به آموزش «مخرج مشترک چیست ، چگونه مخرج مشترک بگیریم؟ — به زبان ساده» مراجعه کنید.
اکنون یک مثال دیگر را با هم حل میکنیم. میخواهیم حاصلِ جمع زیر را بهدست آوریم:
مانند مثال قبل عمل میکنیم. ابتدا اعداد صحیح را با هم جمع کرده، سپس کسرها را با هم جمع میکنیم.
جمع دو عدد صحیح برابر است با:
برای جمع دو کسر، ابتدا مخرج مشترک میگیریم:
با توجه به اینکه کسر حاصل یک کسر ناسره است (یعنی صورتش از مخرجش بزرگتر از یک است و در واقع، کسر بزرگتر از از واحد است)، میتوانیم آن را به یک عدد مخلوط تبدیل کنیم:
در گام آخر، باید دو حدد حاصل از جمع اعداد صحیح و اعداد کسری را با هم جمع کنیم:
روش دوم جمع اعداد مخلوط با مخرج نابرابر
در این روش، ابتدا اعداد مخلوط را به کسر تبدیل میکنیم، سپس برای کسرها مخرج مشترک میگیریم و جمعشان میکنیم. در نهایت نیز، عدد کسری بهدستآمده را به عد مخلوط تبدیل میکنیم. با یک مثال این موضوع را شرح میدهیم.
میخواهیم جمع را محاسبه کنیم. ابتدا، دو عدد را بهصورت کسر مینویسیم:
سپس، از آنجا که مخرجها متفاوت هستند، مخرج مشترک میگیریم. ک.م.م دو عدد و ، عدد است. جمع دو کسر بهصورت زیر خواهد بود:
اکنون باید این کسر را به یک عدد مخلوط تبدیل کنیم:
جمع اعداد مخلوط با شکل
برای جمع اعداد مخلوط (با مخرج یکسان) با کمک شکل، ابتدا، یک شکل واحد رسم میکنیم که نشانه عدد است. سپس مخرج کسرها را میبینیم. مثلاً اگر مخرج کسرها بود، شکلها را به سه قسمت مساوی تقسیم میکنیم. سپس، برای هر عدد صحیح شکل کامل و برای هر کسر، تعداد تکه متناظر از شکل اصلی را در نظر میگیریم. مثلاً اگر یک عدد باشد، یک شکل کامل و یک تکه یکسومی از آن را مشخص میکنیم. برای اعداد دیگر نیز همین کار را میکنیم. در نهایت، تعداد شکلهایی که کامل هستند و تعداد تکهها را میشماریم.
برای مثال، در شکل زیر، دو عدد و با هم جمع شدهاند.
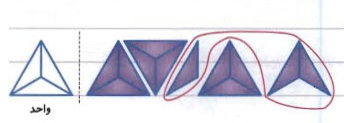
از چپ، دو واحد و یک تکه (یکسوم) را میبینیم که نماینده عدد است. در سمت راست نیز یک مثلث کامل و یک تکه دوتایی عدد را نشان میدهند. اگر مجموع همه اینها را بشماریم، میبینیم که سه مثلث کامل داریم و سه تکه. خود سه تکه یک مثلث کامل را تشکیل میدهند. در نتیجه، چهار مثلث کامل داریم که میشود عدد . یعنی، جواب بهصورت زیر خواهد بود:
جمع اعداد مخلوط روی محور اعداد
برای محاسبه جمع اعداد مخلوط روی محور اعداد، اول از همه، عدد نخست را روی محور مشخص میکنیم. این کار را با کمان جهتدار انجام میدهیم. سپس، از انتهای این کمان، بهاندازه عدد دوم یک کمان دیگر رسم میکنیم. حاصلجمع، برابر با طول کمان از ابتدای کمان مربوط به عدد نخست تا انتهای کمان دوم است.
برای مثال، جمع با کمک محور اعداد، برابر با خواهد بود:
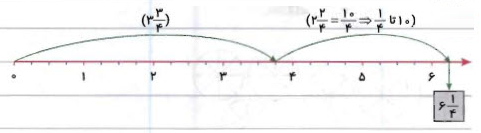
مثالهای جمع اعداد مخلوط
در این بخش، چند مثال را از جمع اعداد مخلوط حل میکنیم.
مثال اول جمع اعداد مخلوط
با استفاده از شکل، جمع دو عدد و را محاسبه کنید.
حل: برای هر واحد یک دایره در نظر میگیریم و با توجه به مخرج کسر، آن را به چهار قسمت مساوی تقسیم میکنیم. برای عدد یک دایره کامل و سه بخش آن را در نظر میگیریم و عدد را با یک دایره و دو بخش کوچک آن مشخص میکنیم.
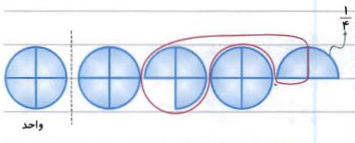
میبینیم که سه دایره کامل و یک بخش کوچک از آن را داریم. بنابراین، جواب بهصورت زیر است:
مثال دوم جمع اعداد مخلوط
با کمک محور اعداد، حاصلجمع را محاسبه کنید.
حل: ابتدا را روی محور مشخص میکنیم و سپس در ادامه آن، عدد را نمایش میدهیم. شکل زیر جمع را نشان میدهد.
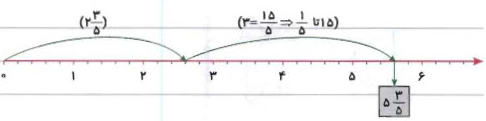
میبینیم که جواب برابر با است.
مثال سوم جمع اعداد مخلوط
حاصلجمع را محاسبه کنید.
حل: برای بهدست آوردن جواب، اعداد صحیح را جدا، و اعداد کسری را جدا با هم جمع میکنیم:
میبینیم که دو عدد کسری، مخرج یکسانی ندارند. بنابراین، باید مخرج مشترک بگیریم و آن دو را با هم جمع کنیم. ک.م.م دو عدد و ، عدد است که مخرج مشترک دو کسر میشود. مراحل زیر، نحوه محاسبه جواب نهایی را نشان میدهند:
مثال چهارم جمع اعداد مخلوط
جمع سه عدد و و را محاسبه کنید.
حل: باید حاصلجمع را بهدست آوریم. مطابق آنچه پیشتر نیز انجام دادیم، اعداد صحیح را جدا و کسرها را جدا با هم جمع میکنیم. چون مخرج کسرها (اعداد و و ) یکسان نیستند، باید مخرج مشترک بگیریم. مخرج مشترک عدد است. در نتیجه، خواهیم داشت:
مثال پنجم جمع اعداد مخلوط
جمع را محاسبه کنید.
حل: این مثال را با روش دیگری حل میکنیم. بهجای آنکه اعداد صحیح را جدا و کسرها را جدا جمع کنیم، ابتدا اعداد مخلوط را به کسر تبدیل و سپس جمعشان میکنیم. مخرج مشترک سه کسر است. جواب بهشکل زیر محاسبه میشود:
جمعبندی
در این آموزش، با روش جمع کردن اعداد مخلوط برای حالتهای مختلف آشنا شدیم. دیدیم که با کمک شکل و محور اعداد میتوان جمع این اعداد را محاسبه کرد. همچنین، روشهای دیگری را همراه با حل مثال برای محاسبه مجموع دو عدد مخلوط بیان کردیم.
آزمون جمع اعداد مخلوط
۱. عدد مخلوط چه اجزایی دارد و صورت کسر آن چه ویژگیای دارد؟
عدد صحیح و یک کسر که صورت از مخرج کوچکتر است.
یک عدد صحیح و دو کسر که صورت هر دو با مخرج برابر است.
فقط یک کسر که صورت از مخرج بزرگتر است.
دو عدد صحیح و یک کسر که صورت از مخرج بزرگتر است.
در عدد مخلوط، یک عدد صحیح و یک کسر وجود دارد که صورت کسر همیشه از مخرج آن کوچکتر است.
۲. تفاوت کلیدی عدد مخلوط با کسر معمولی چیست؟
عدد مخلوط از یک عدد صحیح و یک کسر تشکیل میشود ولی کسر معمولی فقط دو عدد دارد.
کسر معمولی فقط برای تقسیمبندی اشکال هندسی تهیه شده است ولی عدد مخلوط برای محاسبات.
در عدد مخلوط هر دو بخش بزرگتر از مخرج هستند اما در کسر معمولی اینطور نیست.
عدد مخلوط همیشه کوچکتر از یک است ولی کسر معمولی میتواند بزرگتر باشد.
عبارت «عدد مخلوط از یک عدد صحیح و یک کسر تشکیل میشود ولی کسر معمولی فقط دو عدد دارد» درست است، چون عدد مخلوط ترکیبی از یک عدد صحیح و یک بخش کسری است و این موضوع تفاوت اصلی آن با کسر معمولی میباشد. در کسر معمولی فقط صورت و مخرج وجود دارد و خبری از بخش صحیح جداگانه نیست.
۳. در جمع اعداد مخلوط با مخرج برابر، چه دلیلی وجود دارد که گاهی حاصل جمع جزء کسری باید به عدد مخلوط تبدیل شود؟
چون گاهی مجموع جزء کسری از عدد صحیح کمتر باقی میماند.
چون ممکن است مجموع جزء کسری بزرگتر یا مساوی مخرج شود و نیاز به تبدیل به عدد صحیح پیدا کند.
برای اینکه همه نتایج به شکل یکسان نمایش داده شوند و سادهتر باشند.
زیرا جمع جزء کسری نمیتواند صفر باشد و باید تغییر کند.
اگر مجموع جزء کسری اعداد مخلوط در جمع، مقدارش بهاندازه مخرج یا بیشتر شود، باید آن مقدار را به عدد صحیح تبدیل کنیم تا جواب یک عدد مخلوط درست به دست آید. عبارت «ممکن است مجموع جزء کسری بزرگتر یا مساوی مخرج شود و نیاز به تبدیل به عدد صحیح پیدا کند» صحیح است زیرا فقط در این حالت، بخشی از جزء کسری به عنوان واحدِ جدید به عدد صحیح اضافه میشود. گزینههای دیگر موضوع را بیان نمیکنند؛ مثلا همیشه نیاز به تغییر نیست یا هدف فقط یکسانسازی شکل پاسخ نیست و جمع کسری میتواند صفر هم باشد.
۴. برای جمع دو عدد مخلوط با مخرج نابرابر به روش تبدیل به کسر، چه مراحلی باید انجام شود؟
اعداد صحیح را جمع میزنیم و بعد کسرها را جدا هممخرج میکنیم بدون تبدیل به کسر.
فقط جزء کسری هر عدد مخلوط را با هممخرج کردن جمع میکنیم و عدد صحیح را تغییر نمیدهیم.
مخرج مشترک میگیریم، بعد اعداد مخلوط را به کسر تبدیل میکنیم و جواب را مستقیما به عدد صحیح تبدیل میکنیم.
ابتدا اعداد مخلوط را به کسر تبدیل میکنیم، کسرها را هممخرج میکنیم و جمع زده، نتیجه را اگر لازم باشد به عدد مخلوط برمیگردانیم.
برای جمع دو عدد مخلوط با مخرج نابرابر به روش تبدیل به کسر، ابتدا هر عدد مخلوط را به کسر تبدیل میکنیم. سپس کسرهای بهدستآمده را هممخرج کرده و جمع میزنیم. در پایان، اگر حاصل به صورت کسر ناسره باشد، آن را دوباره به عدد مخلوط تبدیل میکنیم.
۵. هنگام نمایش جمع اعداد مخلوط با استفاده از شکلهای هندسی، واحدها باید بر چه مبنایی تقسیم شوند؟
با توجه به بزرگترین عدد مخلوط
بر اساس تعداد اعداد صحیح موجود
بر مبنای عدد صورت کسر هر عدد
مطابق کوچکترین مخرج مشترک
در نمایش جمع اعداد مخلوط به کمک شکلهای هندسی، واحدها بر مبنای مخرج کسر تقسیم میشوند، زیرا باید هر واحد را به بخشهایی به اندازه مساوی تقسیم کرد تا بخش کسری هر عدد بهدرستی روی شکل نمایش یابد. انتخاب «مطابق کوچکترین مخرج مشترک» صحیح است، چون سایر گزینهها مثل تقسیمبندی بر پایه «تعداد اعداد صحیح موجود» یا «عدد صورت کسر»، ارتباطی با ساختار شکل صحیح ندارند و توجه به «بزرگترین عدد مخلوط» نیز تعیینکننده نحوه تقسیم واحد نخواهد بود.
۶. در جمع اعداد مخلوط با مخرج برابر، چه تفاوت یا مزیتی ممکن است هنگام انتخاب میان روش جمع جداگانه جزء صحیح و کسری و روش تبدیل همه اعداد مخلوط به کسر وجود داشته باشد؟
روش جمع جداگانه جزء صحیح و کسری فقط زمانی قابل استفاده است که عدد مخلوط دارای جزء صحیح یکسان باشد.
تبدیل اعداد مخلوط به کسر همیشه باعث میشود پاسخ دقیقتری بدست آید نسبت به جمع جداگانه.
روش جمع جداگانه اغلب محاسبات را سادهتر و سریعتر میکند، بهویژه هنگامی که قسمت کسری کوچک یا ساده باشد.
در هر دو روش، همواره نیاز به سادهسازی کسرها وجود ندارد و نتیجه فقط به شکل عدد صحیح نوشته میشود.
وقتی اجزای کسری ساده هستند، جمع جداگانه جزء صحیح و کسری در محاسبات سرعت و راحتی بیشتری ایجاد میکند، چون نیاز به تبدیل به کسر غیرضروری نیست.













سلام خسته نباشید.استفاده کردیم.ولی مطالب رو خیلی پیچیده عنوان شده مخصوصا مسائل که در ابتدا فرمودید.
با تشکر
با سلام خدمت شما؛
مطلب با این پیشفرض نوشته شده است که با اعداد مخلوط کاملا آشنا هستید و میخواهید نحوه جمع کردن آنها را بیاموزید. پیشنهاد میکنیم برای اینکه بتوانید مسائل ابتدای این مطلب را بهتر متوجه شوید، مطالب «عدد مخلوط چیست و به چه اعدادی می گویند؟ – به زبان ساده» و «تفریق اعداد مخلوط – به زبان ساده + حل تمرین» از مجله فرادرس را مطالعه نمایید. همچنین مشاهده فیلم آموزش رایگان عدد مخلوط + معرفی، ویژگیهای و نحوه نمایش فرادرس نیز میتواند در این زمینه کمککننده باشد.
از همراهی شما با مجله فرادرس سپاسگزاریم.