به توان رساندن ماتریس — آموزش به زبان ساده و با مثال

در مطالب مربوط به ماتریس‌ها در مجله فرادرس، به این موضوع اشاره کردیم که ساختار نمایش نقاط چند بعدی در ریاضیات وابسته به ماتریس‌ها است. به بیان دیگر، می‌توان پدیده‌هایی که توسط چندین متغیر توصیف می‌شوند را به صورت کمیت‌هایی به شکل یک ماتریس بیان کرد. حتی می‌توان ماتریس‌ها را همان اعداد در چندین بُعد در نظر گرفت. پس انتظار داریم که عملیات ریاضی که روی اعداد اجرا می‌کنیم، روی ماتریس‌ها نیز تعریف و به کار گرفته شوند. در این متن از مجله فرادرس می‌خواهیم با توجه به مفهوم توان با استفاده از ضرب برای اعداد، به توان رساندن ماتریس ها را هم مشخص کرده و فراگیریم. در این بین تعریفی که برای به توان رساندن ماتریس های مربعی ارائه می‌کنیم، خوش‌تعریف بوده و اغلب از آن برای به توان رساندن ماتریس استفاده می‌کنند.

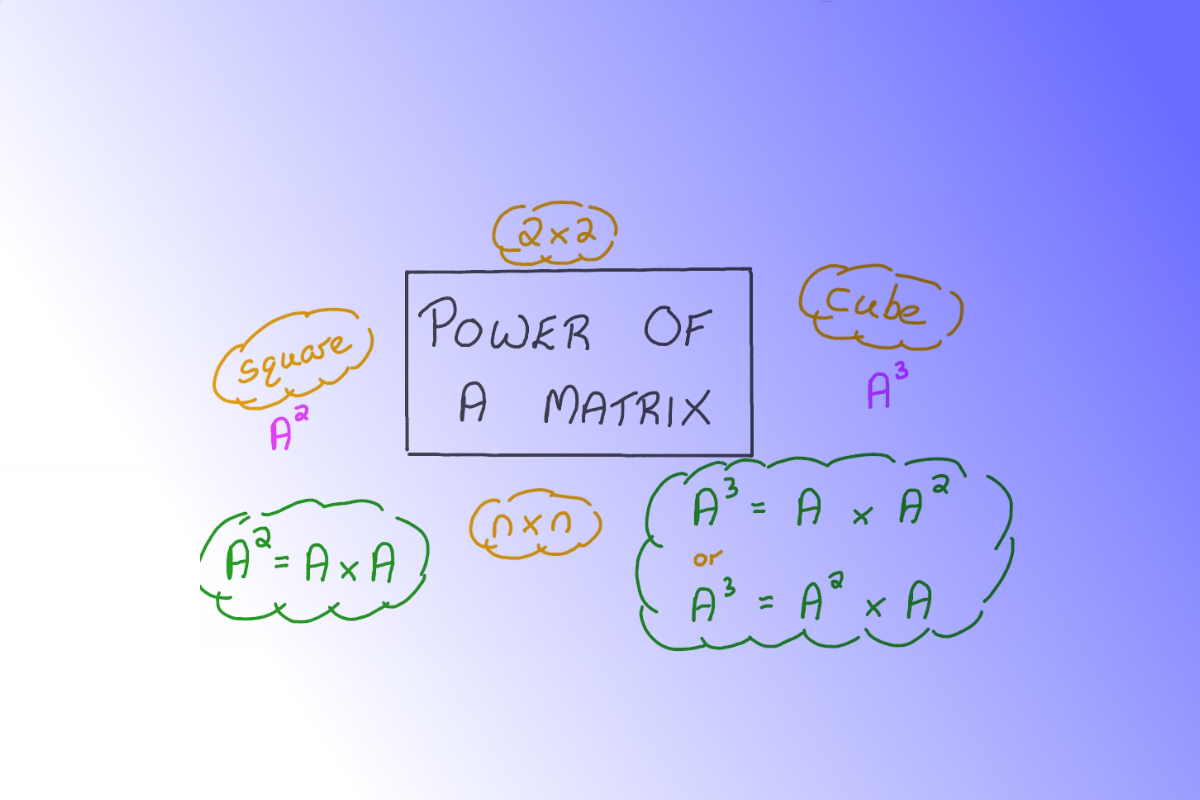
برای مرور کلی مفاهیم ماتریس‌ها و عملیات اولیه قابل اجرا روی آن‌ها بهتر است نوشتارهای دیگر مجله فرادرس مانند ماتریس چیست ؟ | ماتریس در ریاضی — به زبان ساده و خواص ماتریس ها — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب توضیح توان در ریاضیات — به زبان ساده و اعداد توان دار — به زبان ساده نیز خالی از لطف نیست.

به توان رساندن ماتریس

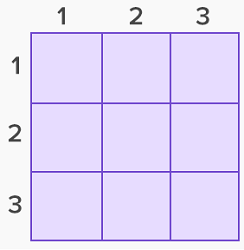
ماتریس‌ها به صورت یک جدول با سطرها و ستون‌های مختلف ساخته می‌شوند که درایه‌ها یا مقادیر آن‌ها در محل تقاطع سطر و ستون‌ها قرار می‌گیرد.

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

در تصویر زیر یک ماتریس سه در سه را مشاهده می‌کنید که باید مقادیر آن در خانه‌های خالی چیده شوند. همانطور که مشخص است منظور از ابعاد یک ماتریس، تعداد سطرها و ستون‌های آن است.

می‌دانید که منظور از توان رساندن یک عدد، ضرب کردن آن در خودش است. برای مثال اگر عدد ۲ را به توان ۳ برسانیم، حاصل برابر است با ۸ زیر با سه بار ضرب کردن عدد ۲ در خودش، به مقدار ۸ خواهیم رسید.

$$\large {\displaystyle 2 ^3 = 2 \times 2 \times 2 = 8 }$$

از همین تعریف برای به توان رساندن ماتریس نیز می‌توان استفاده کرد. به این معنی که با ضرب کردن یک ماتریس در خودش، آن را به توان می‌رسانیم. فقط توجه داشته باشید که توان رساندن در اینجا به صورت توان‌های صحیح از یک ماتریس است.

به توان رساندن ماتریس مربعی

بنابراین اگر $$A$$ یک ماتریس مربعی باشد، $$A^2$$ را به صورت زیر تعریف می‌کنیم.

$$\large {\displaystyle A^2 = A \times A }$$

نکته: به این علت، ماتریس را مربعی در نظر گرفته‌ایم، تا تعداد سطر و ستون‌های آن برابر بوده و بتوان آن را در خودش ضرب کرد.

مثال ۱

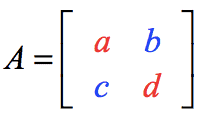
اگر ماتریس $$A$$ به صورت زیر باشد، آنگاه $$A^2$$ را بدست آورید و عمل به توان رساندن ماتریس را اجرا کنید.

$$\large {\displaystyle \begin{bmatrix}a & b \\ c & d \end{bmatrix} }$$

همانطور که گرفته شد، باید این ماتریس را در خودش ضرب کنیم و از قاعده ضرب ماتریس‌ها کمک بگیریم. از آنجایی که ماتریس مربعی و $$2 \times 2$$ است، به صورت زیر عمل می‌کنیم.

$$\large {\displaystyle A^2 = \begin{bmatrix}a & b \\c & d \end{bmatrix}  \times \begin{bmatrix}a & b \\c & d \end{bmatrix} }$$

فیلم آموزش جبر خطی – مرور و حل مساله در فرادرس

کلیک کنید

در نتیجه حاصل ضرب به صورت زیر در خواهد آمد.

$$\large {\displaystyle \begin{bmatrix} a^2 + b c & a b + b d \\ c a + d c & c b + d^2 \end{bmatrix} }$$

مثال ۲

با توجه به رابطه بالا، برای ماتریس $$A$$ که در زیر معرفی شده، توان دوم را محاسبه کنید.

$$\large {\displaystyle A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} }$$

مشخص است که در اینجا مقادیر به صورت زیر هستند.

$$\large {\displaystyle \begin{bmatrix}  a  = 1 &  b = 2 \\ c = 3 & d = 4 \end{bmatrix} }$$

پس مربع یا توان دوم ماتریس $$A$$ برابر است با ماتریس زیر:

$$\large {\displaystyle \begin{bmatrix} 1^2 + 2 \times 3 & (1 \times 2) + (2 \times 4) \\ ( 3 \times 1)  + (4 \times 3)  & (3 \times 2)  + 4^2 \end{bmatrix}  = \displaystyle \begin{bmatrix} 7 &  1  0 \\ 1 5 & 2 2 \end{bmatrix} }$$

به همین ترتیب اگر لازم باشد، به توان رساندن ماتریس را براساس توان‌های بزرگتر از ۲ انجام داد، کافی است که تعداد ضرب‌ها را بیشتر کرد. مثلا اگر هدف به توان رساندن ماتریس A با درجه ۴ باشد، باید ماتریس $$A^2$$ را در خودش ضرب کرد.

$$\large A^4 = (A^2 ) ^2 = {\displaystyle \begin{bmatrix} 7 &  1 0 \\ 1 5 & 2 2 \end{bmatrix} \times \begin{bmatrix} 7 &  1 0 \\ 1 5 & 2 2 \end{bmatrix} }$$

که نتیجه به صورت یک ماتریس دو در دو و به شکل زیر خواهد بود.

$$\large A^4 = (A^2 ) ^2 = {\displaystyle \begin{bmatrix} 1 9 9  &  2 9 0  \\ 4 3 5 & 6 3 4  \end{bmatrix}}$$

البته اگر به جای به توان رساندن ماتریس $$A^2$$ از چهار بار ضرب ماتریس $$A$$ در خودش استفاده می‌کردید، باز هم حاصل توان رساندن ماتریس یکسان بود. بنابراین تعریف به کار رفته در به توان رساندن ماتریس مربعی، خوش تعریف است.

نکته: توجه داشته باشید که توان‌های به کار رفته برای اجرا عمل به توان رساندن ماتریس ها باید حتما مقداری مثبت داشته و از مجموعه اعداد صحیح باشد.

همچنین محاسبه ماتریس $$A^k$$ نیز به شکل زیر انجام می‌شود.

$$\large {\displaystyle \mathbf {A } ^{ k} = \underbrace {\mathbf {A} \mathbf {A} \cdots \mathbf {A} }_{ k{ \text{ times}}}}$$

مثال ۳

این بار فرض می‌کنیم که ماتریس مورد نظرمان یعنی ماتریس $$A$$، یک ماتریس قطری باشد، به توان رساندن ماتریس در این حالت همان به توان رساندن عناصر قطر اصلی است. برای مثال فرض کنید ماتریس $$A$$ را به صورت زیر در نظر گرفته‌ایم.

$$\large A = {\displaystyle \begin{bmatrix} 3   &  0 & 0 \\ 0 & 2 & 0  \\ 0  & 0 & 5  \end{bmatrix}}$$

فیلم آموزش جبر خطی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

به این ترتیب $$A^3$$ برابر است با ماتریس زیر:

$$\large A^3  = {\displaystyle \begin{bmatrix} 3^3   &  0 & 0 \\ 0 & 2^3 & 0  \\ 0  & 0 & 5^3   \end{bmatrix} =  {\displaystyle \begin{bmatrix} 27   &  0 & 0 \\ 0 & 8 & 0  \\ 0  & 0 & 125  \end{bmatrix}}}$$

همانطور که دیده می‌شود، فقط عناصر روی قطر اصلی، به توان ۳ رسیده‌اند و بقیه عناصر، صفر هستند. در نتیجه حاصل به توان رساندن ماتریس قطری، باز هم یک ماتریس قطری است که درایه‌های قطر اصلی در آن، به توان رسیده‌اند.

مثال 5

ماتریس زیر را در نظر بگیرید که قرار است مربع آن یعنی حاصل ضرب آن در خودش را محاسبه کنیم.

$$\large {\displaystyle  I = {\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}} }$$

می‌دانید که ماتریس بالا، ماتریس همانی یا یکه است زیرا یک ماتریس قطری مربع است که عناصر قطر اصلی آن همگی برابر با ۱ هستند. این ماتریس را به عنوان ماتریس خنثی در عمل ضرب ماتریسی می‌شناسیم. به این معنی که ضرب آن در هر ماتریسی، برابر با خود آن ماتریس خواهد شد. حال ماتریس همانی را در خودش ضرب می‌کنیم تا مربع آن را بدست آوریم.

$$\large {\displaystyle  I^2 = I \times I = {\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}} \times {\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}} }$$

مشخص است که این حاصل ضرب همان ماتریس همانی خواهد بود، زیرا ماتریس $$I$$‌عامل خنثی ضرب ماتریس‌ها است. پس داریم.

$$\large {\displaystyle  I^2 = I \times I = I = {\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}}  }$$

چنین ماتریسی را یک «ماتریس خود توان» (Idempotent matrix) می‌نامند زیرا مربع یا توان دوم آن، تفاوتی با خودش نداشته ایجاد و حاصل ضرب هر ماتریس خودتوان در خودش برابر با خود ماتریس خودتوان خواهد بود.

نکته: به طور کلی تمامی ماتریس‌های همانی در هر ابعادی، خودتوان هستند.

مثال ۶

نشان دهید که ماتریس زیر یک ماتریس خودتوان است.

$$\large A = {\displaystyle \begin{bmatrix} 3 & - 6 \\ 1 & - 2 \end{bmatrix}}$$

برای مشخص کردن این خاصیت برای ماتریس بالا، کافی است که مربع یا توان دوم این ماتریس را محاسبه کنیم.

$$\large A^2 = A \times A = {\displaystyle \begin{bmatrix} 3 & - 6 \\ 1 & - 2 \end{bmatrix} \times \begin{bmatrix} 3 & - 6 \\ 1 & - 2 \end{bmatrix} =}$$

$$\large {\displaystyle \begin{bmatrix} 3 & - 6 \\ 1 & - 2 \end{bmatrix} = A }$$

مثال ۷

ماتریس زیر نیز یک ماتریس خودتوان است زیرا مربع یا حاصل ضرب آن در خودش، با خود ماتریس برابر است.

$$\large {\displaystyle B = {\begin{bmatrix}2 & - 2 & - 4 \\- 1 & 3 & 4 \\ 1 & - 2 & - 3 \end{bmatrix}}}$$

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

$$\large {\displaystyle B \times B = B^2 = {\begin{bmatrix}2 & - 2 & - 4 \\- 1 & 3 & 4 \\ 1 & - 2 & - 3 \end{bmatrix}}}$$

به توان رساندن ماتریس غیر مربعی

ضرب ماتریس‌ها با ضرب اعداد تفاوت دارد. در اینجا باید عملیات به صورت خاصی صورت گیرد. در تصویر زیر حاصل ضرب درایه های سطر اول ماتریس A را در درایه‌های ستون اول ماتریس B مشاهده می‌کنید که مجموع این حاصل‌ضرب‌ها به عنوان اولین درایه حاصل ضرب ماتریس‌ها شناخته خواهد شد. به همین ترتیب، درایه مربوط به سطر دوم و ستون اول، حاصل از ضرب سطر دوم ماتریس A در ستون اول ماتریس B بوده که با یکدیگر جمع می‌شوند.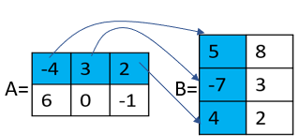

همانطور که دیدید، ضرب یک ماتریس مربعی در خودش، با توجه به یکسان بودن تعداد سطر و ستون‌ها، به راحتی امکان‌پذیر است. ولی اگر ماتریس مورد نظر، مربعی نباشد، ضرب یک ماتریس در خودش، امکان‌پذیر نیست.

در این حالت برای به توان رساندن ماتریس از ضرب یک ماتریس در ترانهاده‌اش استفاده می‌کنیم. بنابراین اگر $$B$$ ماتریس مورد نظر ما باشد، مثلا $$B^2$$ به شکل زیر بدست می‌آید.

$$\large {\displaystyle B^2 = B \times B ^{\prime }}$$

بنابراین اگر ماتریس $$B$$ دارای $$n$$ سطر و $$m$$ ستون باشد، آنگاه ترانهاده آن دارای $$m$$ سطر و $$n$$ ستون است. به این ترتیب حاصل ضرب آن‌ها، یک ماتریس $$n$$ در $$n$$ خواهد بود. از طرفی می‌توان این ضرب را به شکل دیگری نیز انجام داد و ابتدا ترانهاده ماتریس را در آن ضرب کرد. به این ترتیب رابطه زیر نیز قابل تعریف است.

$$\large {\displaystyle B^2 = B ^{\prime } \times B }$$

که حاصل یک ماتریس مربعی $$m \times m$$ خواهد بود. به همین جهت، به توان رساندن ماتریس غیرمربعی مرسوم نبوده و خوش تعریف نیست، زیرا به دو شکل قابل محاسبه است که نتیجه یکسانی نیز ندارند.

مثال 8

این بار یک ماتریس غیر مربعی را در خودش ضرب می‌کنیم. فرض کنید ماتریس $$B$$ به صورت زیر است. مشخص است که این یک ماتریس $$2 \times 3$$ است.

$$\large {\displaystyle B = \begin{bmatrix} 1 & 2 & 3 \\ 4  & 5 & 6 \end{bmatrix} }$$

به این ترتیب ترانهاده آن به شکل زیر خواهد بود.

$$\large {\displaystyle B^{ \prime} = \begin{bmatrix} 1 & 4 \\ 2  & 5 \\ 3 & 6 \end{bmatrix} }$$

در نتیجه مربع ماتریس $$B$$ به دو صورتی که گفته شد، به شکل زیر نوشته خواهد شد.

$$\large {\displaystyle B ^2 = \begin{bmatrix} 1 & 2 & 3 \\ 4  & 5 & 6 \end{bmatrix}  \times \begin{bmatrix} 1 & 4 \\ 2  & 5 \\ 3 & 6 \end{bmatrix}  }$$

که در این حالت، نتیجه برابر با ماتریس مربعی $$2 \times 2$$ زیر است.

$$\large  B^2 = {\displaystyle \begin{bmatrix}  4 9  &  3 2  \\ 3 2 & 7 7   \end{bmatrix}}$$

مثال 9

این بار در صورتی که ابتدا ماتریس ترانهاده را ضرب کنیم، ماتریس حاصل، یک ماتریس مربعی $$3 \times 3$$ می‌شود.

$$\large {\displaystyle B ^2 = \begin{bmatrix} 1 & 4 \\ 2  & 5 \\ 3 & 6 \end{bmatrix}  \times \begin{bmatrix} 1 & 2 & 3 \\ 4  & 5 & 6 \end{bmatrix}   = }$$

$$\large {\displaystyle  \begin{bmatrix} 1 7  & 2 2 &  2 7  \\  2 2 & 2 9  & 3 6 \\ 2 7 &   3 6 & 4 5 \end{bmatrix} }$$

مشخص است که هنگام به توان رساندن ماتریس غیر مربعی، پاسخ‌ها یکسان نبوده و توان رساندن در این حالت، خوش‌تعریف نیست.

نکته: ریشه گرفتن از یک ماتریس، به معنی آن است که ماتریسی را پیدا کنیم که حاصل ضرب آن در خودش، برابر با ماتریس مورد نظر باشد. در اینجا به این مبحث نخواهیم پرداخت ولی توجه داشته باشید که در این حالت باید ماتریس مورد نظر، معین مثبت (Positive Definite) باشد. به یاد داشته باشید که گاهی توان معکوس را به صورت ریشه‌گیری نیز نشان می‌دهند. به این ترتیب اگر ماتریسی را به توان $$\tfrac{1}{2}$$ برسانیم، به مانند محاسبه ریشه دوم ماتریس خواهد بود. به این ترتیب حاصل ریشه دوم یک ماتریس، ماتریسی خواهد بود که ضرب آن در خودش، ماتریس اولیه را بسازد.

خلاصه و جمع‌بندی

در این متن به بررسی نحوه به توان رساندن ماتریس ها پرداختیم و همانطور که اعداد را به کمک ضرب کردن، توان‌های صحیح یک ماتریس مربعی را نیز شرح دادیم. در این بین مشخص شد که برای ماتریس‌های غیر مربعی به کار بردن تعریف به توان رساندن ماتریس ها معنی‌دار نبوده و خوش‌تعریف نیست. همچنین با ذکر مثالی تفاوت به توان رساندن ماتریس مربعی و غیر مربعی را مشخص کردیم. در این بین دیدیم که برای ضرب یک ماتریس غیر مربعی در خودش، دو راهکار وجود دارد که هر کدام را می‌توان تعریفی برای به توان رساندن ماتریس در نظر گرفت. ولی به علت ناسازگاری آن‌ها، کمتر از این نوع محاسبات برای توان رساندن ماتریس‌های غیر مربعی استفاده می‌شود.