اتحاد مربع چیست؟ — اثبات، فرمول و نمونه سوال با جواب

در آموزش‌های پیشین مجله فراردس، با اتحاد و تجزیه در ریاضی آشنا شدیم. همچنین، برخی از اتحادها، مانند اتحاد مکعب دوجمله‌ای، اتحاد مکعب، اتحاد چاق و لاغر و اتحاد مزدوج را معرفی کردیم و در مطلبی به حل نمونه سؤالات اتحاد و تجزیه پرداختیم. اتحاد مربع یکی از رایج‌ترین اتحادهای جبری است که در این آموزش مطالبی را درباره آن بیان می‌کنیم.

اتحاد چیست؟

یک اتحاد جبری برای همه مقادیر و متغیرها برقرار است و در موقعیت‌های مختلف می‌توان از یکی از دو طرف تساوی به‌عنوان عبارت برابر با طرف دیگر استفاده کرد. برای مثال، می‌توان به‌جای $$(a-b)^ 2$$، عبارت جبری $$a ^ 2 - 2 a b + b ^ 2$$ را قرار داد و بالعکس.

یکی از کاربردها اتحادها این است که با استفاده از آن‌ها می‌توان به‌راحتی حل بسیاری از مسائل پیچیده را آسان کرد، عبارت‌های جبری را تجزیه کرد و... .

در ادامه، با اتحاد مربع آشنا می‌شویم و مثال‌های متنوعی را از کاربرد آن بررسی خواهیم کرد.

برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

اتحاد مربع چیست ؟

اتحاد مربع به اتحادی می‌گویند که در آن یک دوجمله‌ای (جمع یا تفریق دو جمله)، سه‌جمله‌ای و... به توان ۲ برسد. اتحاد مربع دو‌جمله‌ای و اتحاد مربع سه‌جمله‌ای از مهم‌ترین و رایج‌ترین اتحادهای مربع هستند. در ادامه با این اتحادها آشنا می‌شویم.

اتحاد مربع دو جمله ای

اتحاد مربع دوجمله‌ای برای دو حالت مجموع و تفاضل دو جمله بیان می‌شود که به‌ترتیب، به‌نام اتحاد نوع اول و اتحاد نوع دوم مشهور هستند.

اتحاد مربع جمع دو جمله‌

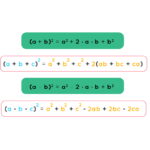
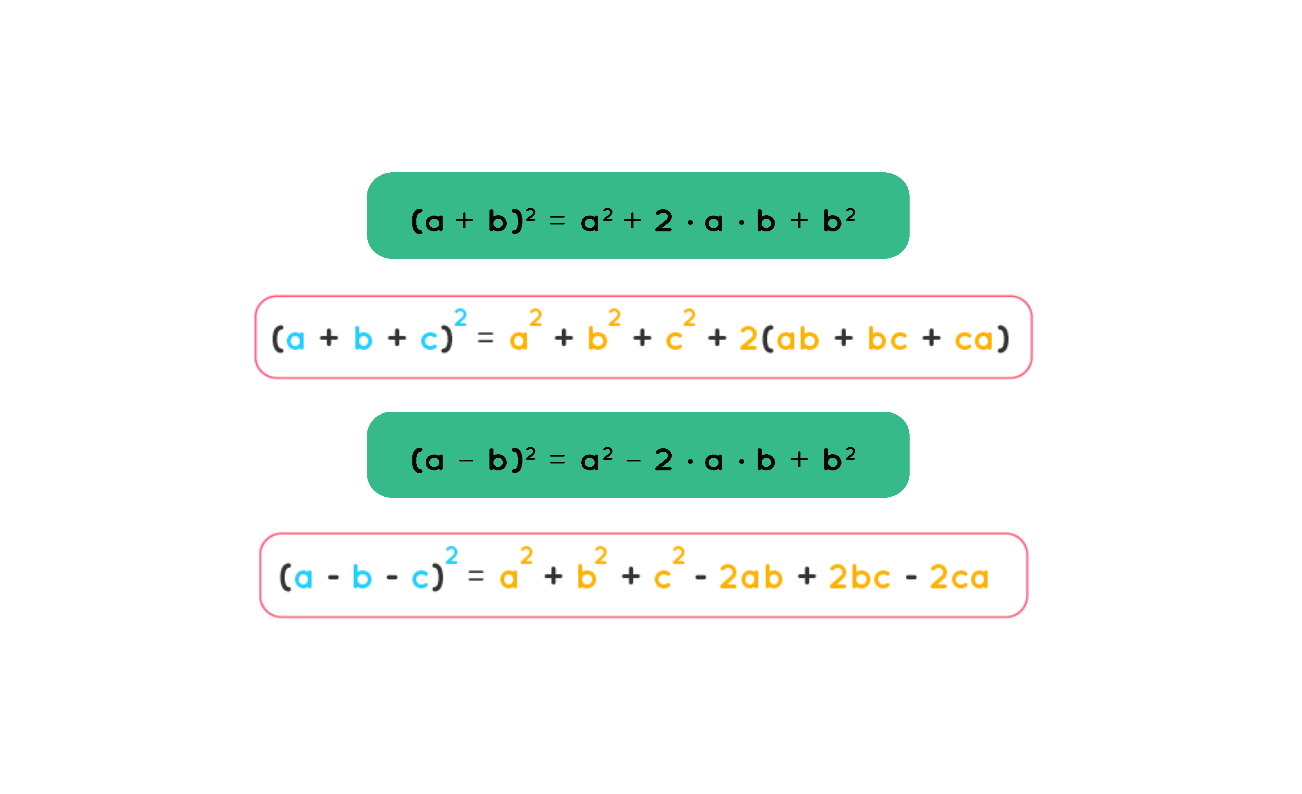
اتحاد مربع برای جمع دو جمله عمومی $$a$$ و $$b$$ به‌صورت زیر بیان می‌شود:

$$\large ( a - b ) ^ 2 = a ^ 2 - 2 a b + b ^ 2$$

اثبات اتحاد مربع مجموع دو جمله

برای اثبات اتحاد مربع، یک راه ساده این است که سمت چپ اتحاد، یعنی عبارتی را که به توان دو رسیده است، ساده کنیم. بدین ترتیب، خواهیم داشت:

$$\large \begin{aligned} ( a + b ) ^ 2 & = ( a + b ) ( a + b ) \\ & = a ( a + b ) + b ( a + b ) \\ & = a ^ 2 + a b + b a +b ^ 2 \\ & = a ^ 2 + 2 a b + b ^ 2 \end{aligned}$$

می‌بینیم که طرف اول و دوم اتحاد با هم برابرند و بنابراین، اثبات کامل می‌شود.

یک راه دیگر اثبات اتحاد مربع جمع دو جمله، استفاده از شکل است. برای اثبات اتحاد مربع با شکل، فرض کنید مربعی به ضلع $$( a + b )$$ داریم. این مربع در شکل زیر نشان داده شده است.

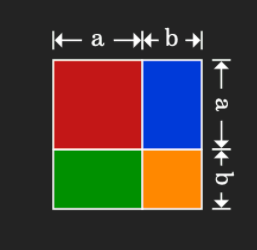
همان‌طور که می‌دانیم، مساحت یک مربع با به توان دو رساندن اندازه ضلع آن به‌دست می‌آید که برای این مربع برابر است با

$$\large ( a + b ) ^ 2$$

اما، همان‌طور که مشاهده می‌کنیم، مساحت این مربع خود از چهار مساحت تشکیل شده است:‌

• مربعی به ضلع $$a$$
• مستطیلی به عرض $$b$$ و طول $$a$$
• مربعی به ضلع $$b$$
• مستطیلی به عرض $$b$$ و طول $$a$$

مجموع مساحت‌های این چهار شکل، برابر است با

$$\large a ^ 2 + a b + ab + b ^ 2  = a ^ 2 + 2 a b + b ^ 2$$

از آنجا که مساحت مربع برگ برابر با مساحت این چهار شکل است، خواهیم داشت:‌

$$( a + b ) ^ 2 = a ^ 2 + 2 a b + b ^ 2$$

اتحاد مربع تفاضل دو جمله‌

در کنار اتحاد مربع، اتحاد نوع دوم نیز معرفی می‌شود که تفاوت آن در علامت‌هاست. اتحاد مربع تفاضل دو جمله‌ به‌صورت زیر بیان می‌شود:

$$\large ( a - b ) ^ 2 = a ^ 2 - 2 a b + b ^ 2$$

اثبات اتحاد مربع تفاضل دو جمله

برای اثبات اتحاد مربع تفاضل دو جمله، یک راه ساده این است که سمت چپ اتحاد، یعنی عبارتی را که به توان دو رسیده است، ساده کنیم. بدین ترتیب، خواهیم داشت:

$$\large \begin{aligned} ( a - b ) ^ 2 & = ( a - b ) ( a - b ) \\ & = a ( a - b ) - b ( a - b ) \\ & = a ^ 2 - a b - b a +b ^ 2 \\ & = a ^ 2 - 2 a b + b ^ 2 \end{aligned}$$

می‌بینیم که طرف اول و دوم اتحاد با هم برابرند و بنابراین، اثبات کامل می‌شود.

یک راه دیگر اثبات اتحاد مربع تفاضل دو جمله، استفاده از شکل است. برای اثبات اتحاد مربع با شکل، فرض کنید مربعی به ضلع $$a$$ داریم که هر ضلع آن را به دو بخش $$b$$ و $$a - b$$ تقسیم می‌کنیم. این مربع در شکل زیر نشان داده شده است.

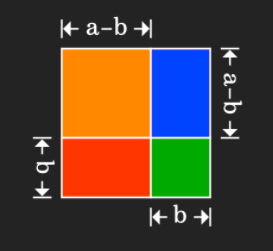
همان‌طور که می‌دانیم، مساحت یک مربع با به توان دو رساندن اندازه ضلع آن به‌دست می‌آید که برای این مربع برابر است با

$$\large a ^ 2$$

اما، همان‌طور که مشاهده می‌کنیم، مساحت این مربع خود از چهار مساحت تشکیل شده است:‌

• مربعی به ضلع $$a-b$$
• مستطیلی به عرض $$b$$ و طول $$a-b$$
• مربعی به ضلع $$b$$
• مستطیلی به عرض $$b$$ و طول $$a$$

بنابراین، خواهیم داشت:

$$\large \begin {align*} (a-b) ^ 2 + (a-b) b + (a-b)b + b ^ 2  & = a ^ 2 \\ (a-b)^2 +ab - b^2+ab - b ^ 2 + b^ 2 &= a ^ 2 \\ (a -b ) ^ 2 + 2 a b - b ^ 2 = a ^ 2 \\ ( a - b ) ^ 2 = a ^ 2 - 2 a b + b ^ 2 \end {align*}$$

می‌بینیم که طرف اول و دوم اتحاد با هم برابرند و بنابراین، اثبات کامل می‌شود.

اتحاد مربع‌ سه جمله ای

اتحاد مربع سه‌جمله‌ای برای دو حالت مجموع و تفاضل سه جمله بیان می‌شود که در ادامه با آن‌ها آشنا می‌شویم.

اتحاد مربع‌ مجموع سه جمله

اتحاد مربع مجموع سه جمله $$a$$ و $$b$$ و $$c$$ به‌‌صورت زیر است:

$$\large \begin {aligned} ( a + b + c ) ^ { 2 } = a ^ { 2 } + b^ { 2 } +c ^ { 2 } + 2( a b + b c + c a ) \end {aligned}$$

اثبات اتحاد مربع‌ مجموع سه جمله

برای اثبات اتحاد مربع سه‌جمله‌ای کافی است ضرب $$( a + b + c ) ( a + b + c )$$ را انجام دهیم:

$$\large \begin {aligned} & ( a + b + c ) ^ { 2 } = ( a + b + c ) ( a + b + c ) \\ & = a ^ { 2 } + a b + a c + a b + b ^ { 2 } + b c + c a + b c + c ^ { 2 } \\ & = a ^ { 2 } + b ^ { 2 } +c ^ { 2 } + 2 a b + 2 b c + 2 c a \\ & = a ^ { 2 } + b^ { 2 } +c ^ { 2 } + 2( a b + b c + c a ) \end {aligned}$$

می‌بینیم که اتحاد به‌‌سادگی اثبات می‌شود.

اتحاد مربع‌ تفاضل سه جمله

اتحاد مربع تفاضل سه جمله به‌صورت زیر است:

$$\large ( a - b - c ) ^ { 2 } = a ^ { 2 } + b ^ { 2 } + c ^ { 2 } - 2 a b + 2 b c - 2 c a$$

اثبات اتحاد مربع‌ تفاضل سه جمله

این اتحاد نیز به‌سادگی به‌صورت زیر اثبات می‌شود:

$$\large \begin {aligned} ( a - b - c ) ^ { 2 } & = ( a - b - c ) ( a - b - c ) \\ & = a ^ { 2 } - a b - a c - a b + b ^ { 2 } + b c - c a + b c + c ^ { 2 } \\ & = a ^ { 2 } + b ^ { 2 } + c ^ { 2 } - 2 a b + 2 b c- 2 c a \\ & = a ^ { 2 } +b ^ { 2 } + c ^ { 2 } - 2 ( a b - b c + c a ) \end {aligned}$$

مثال‌های اتحاد مربع‌

در این بخش، مثال‌هایی را از اتحاد مربع بیان می‌کنیم.

مثال اول اتحاد مربع‌

با استفاده از اتحاد مربع سه‌جمله‌ای، مقدار عبارت $$a ^ 2 + b ^ 2 + c ^ 2$$ را با توجه به تساوی‌های $$a + b + c = 20$$ و $$ab + bc + ca = 20$$ به‌دست آورید.

حل: با استفاده از اتحاد مربع سه‌جمله‌ای، می‌توان نوشت:

$$\large a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ca)$$

بنابراین، داریم:

$$\large a ^ 2 + b ^ 2 + c ^ 2 = ( 2 0 ) ^ 2 - 2 ( 2 0 ) = 400 - 40 = 360$$

مثال دوم اتحاد مربع‌‌

اگر $$a = 12$$، $$b = 4$$ و $$c = 5$$ باشد، مقدار $$( a - b - c ) ^ 2$$ را محاسبه کنید.

حل: با توجه به اتحاد مربع تفاضل سه جمله که بیان کردیم، داریم:

$$\large \begin {aligned} ( a - b - c ) ^ { 2 } & = a ^ { 2 } + b ^ { 2 } + c ^ {2 } - 2 a b + 2 b c - 2 c a \\ & = 1 2 ^ { 2 } + 4 ^ { 2 }+ 5 ^ { 2 } - 2 ( 1 2 ) ( 4 ) + 2 ( 4 ) ( 5 ) - 2( 5 ) ( 1 2 ) \\ & = 1 4 4 + 1 6 + 2 5- 9 6+ 4 0 - 1 2 0 \\ &= 9 \end{aligned}$$

مثال سوم اتحاد مربع‌

فرض کنید $$r$$ یک عدد حقیقی است، به‌گونه‌ای که $${ r } ^ { 2 } - 6 r + 5 = 0$$. مقدار $$( r - 3 ) ^ 2$$ را محاسبه کنید.

حل: یک راه ساده این است که عبارت را به‌فرم اتحاد مربع در آوریم. برای این کار، می‌توانیم یک عدد $$4$$ را به دو طرف معادله اضافه کنیم. چون به هر دو طرف معادله عدد $$4$$ را اضافه کرده‌ایم، تغییری در جواب آن حاصل نمی‌شود.

بنابراین، خواهیم داشت:

$$\large \begin {align} (r^ 2 - 6 r + 5 )+ 4 & = 0 + 4 \\ r ^ 2 - 6 r + 9 & = 4 \\ ( r - 3 ) ^ 2 & = 4 \\ \end {align}$$

در نتیجه، مقدار عبارت برابر با $$4$$ است.

مثال چهارم اتحاد مربع‌

مقدار عبارت عددی زیر را محاسبه کنید:

$$\large 73 ^ 2 + 2 \times 27 \times 73 + 27 ^ 2$$

حل: فرض می‌کنیم $$a = 73$$ و $$b = 27$$ باشد. در این‌‌صورت، خواهیم داشت:

$$\large a ^ 2 + 2 \times b \times a + b ^ 2 = ( a + b) ^ 2 = 100 ^ 2 = 10000$$

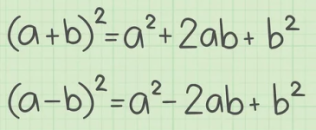
مثال پنجم اتحاد مربع‌

عبارت زیر را تجزیه کنید.

$$\large n ^ 4 + 4$$

حل: باید این عبارت را به مربع کامل تبدیل کنیم. بدین منظور، جمله $$4 n ^ 2$$ را به عبارت اضافه و از آن کم می‌کنیم. بنابراین، خواهیم داشت:

$$\large n ^ 4 + 4 n ^ 2 + 4 - 4 n ^ 2 = ( n ^ 2 + 2 ) ^ 2 - 4 n ^ 2$$

اکنون از اتحاد مزدوج استفاده می‌کنیم و می‌نویسیم:

$$\large ( n ^ 2 + 2 ) ^ 2 - 4 n ^ 2 = ( n ^ 2 + 2 ) ^ 2 - ( 2 n ) ^ 2 = ( n ^ 2 + 2 + 2 n ) ( n ^ 2 + 2 - 2 n )$$

مثال ششم اتحاد مربع‌

آیا اعداد حقیقی و متمایز $$a$$ و $$b$$ و $$c$$ و $$d$$ وجود دارند که در معادله زیر صدق کنند:‌

$$\large { a ^ 2 + b ^ 2 + c ^2 + d ^ 2 = a b + b c + c d + d a }$$

حل: ابتدا، عدد $$2$$ را در این معادله ضرب می‌کنیم، سپس سمت راست آن را به سمت چپ می‌آوریم:

$$\large 2 ( a ^ 2 + b ^ 2 + c ^ 2 + d ^ 2 ) - 2 ( a b + b c + c d + d a ) = 0$$

جملات را به‌صورت زیر در کنار هم قرار می‌دهیم:

$$\large ( a ^ 2 - 2 a b + b ^ 2 ) + ( b ^ 2 - 2 b c + c ^ 2 ) + ( c ^ 2 - 2 c d + d ^ 2 ) + ( d ^ 2 - 2 d a + a ^ 2 ) = 0$$

اکنون از اتحاد مربع استفاده می‌کنیم و تساوی زیر را خواهیم داشت:

$$\large ( a - b ) ^ 2 + ( b - c ) ^ 2 + ( c - d ) ^ 2 + ( d - a ) ^ 2 = 0$$

همان‌طور که می‌بینیم، طرف چپ تساوی مجموع چهار مربع کامل است. مربع کامل نیز تنها می‌تواند مثبت یا صفر باشد. بنابراین، برای آنکه تساوی برقرار باشد، باید چهار مربع کامل برابر با صفر باشند:

$$\large ( a - b ) ^ 2 = ( b - c ) ^ 2 = ( c - d ) ^ 2 = ( d - a ) ^ 2 = 0$$

در نتیجه، باید داشته باشیم:

$$\large a − b = b − c = c − d = d − a = 0$$

این یعنی اینکه $$a = b = c = d$$ که متناقض با مجزا بودن $$a$$ و $$b$$ و $$c$$ و $$d$$ است. در نتیجه، پاسخ به سؤال، خیر است.

مثال هفتم اتحاد مربع‌

اگر $$a + b + c = 200$$ و $$ab + bc + ca = 10000$$، آنگاه مقدار $$a ^ 2 + b ^ 2 + c ^ 2$$ را محاسبه کنید.

حل: با استفاده از اتحاد مربع سه‌جمله‌ای می‌توان نوشت:

$$\large \begin {aligned} a ^ { 2 } + b ^ { 2 } + c ^ { 2 } & = ( a + b + c ) ^ { 2 } - 2 ( a b + b c + c a ) \\ & = ( 2 0 0 ) ^ { 2 } - 2 ( 1 00 0 0 ) = 4 00 0 0 - 20 0 0 0= 20000 \end {aligned}$$

مثال هشتم اتحاد مربع‌

تساوی‌های زیر داده شده‌اند:

$$\large \begin {aligned} a + b & = c + 6 \\ a b - a c & = b c - 1 \\ \end {aligned}$$

مقدار $$a ^ 2 + b ^ 2 + c ^ 2$$ را محاسبه کنید.

حل: با استفاده از مقادیری که داده شده، خواهیم داشت:

$$\large \begin {array} {lll} a ^ 2 + b ^ 2 + c ^ 2 & ={ ( a + b + c ) } ^ 2 - 2 ( a b + b c + ac ) \\ & = { ( ( c +6 ) + c ) }^ 2 - 2 ( ( b c + a c - 1 ) + b c + a c ) \\ & = { ( 2 c + 6 ) } ^ 2 - 2 ( 2 b c + 2 a c - 1 ) \\ & = { ( 4 c ^ 2 + 2 4 c + 3 6 ) } - 2 ( 2 c (b + a ) - 1 ) \\ & = { ( 4 c ^ 2 + 2 4 c+ 3 6) } - 2 ( 2 c ( c + 6 ) - 1 ) \\ & = { ( 4 c ^ 2 + 2 4 c + 3 6 ) } - ( 4 c ^ 2+ 2 4 c - 2 ) \\ & = 36 - ( - 2 ) = 36 + 2 = 38 \end {array}$$

مثال نهم اتحاد مربع‌‌

مقدار $$6 ^ 4$$ را با استفاده از اتحاد مربع محاسبه کنید.

حل: این عبارت را می‌توان به‌شکل زیر نوشت:

$$\large 6 ^ 4 = (( 3 + 3 ) ^ 2 ) ^ 2$$

در واقع عبارت بالا این‌گونه است، که در آن، $$a = 3$$ و $$b = 3$$:

$$\large (( a + b ) ^ 2 ) ^ 2$$

با استفاده از اتحاد مربع، عبارت داخلی برابر است با

$$\large ( 3+ 3) ^2 = 3 ^ 2 + 2 ( 3 ) ( 3 ) + 3 ^ 2 = 36$$

بنابراین، داریم:

$$\large 64 ^ 4 = 36 ^ 2$$

باز هم می‌توانیم از اتحاد مربع استفاده کنیم و بنویسیم:

$$\large \begin {align} 36 ^ 2 & = ( 30 + 6 ) ^ 2 = 3 0^ 2 + 2 ( 30 ) ( 6 ) + 6 ^ 2 \\ & = 900+ 360+ 36 \\ & = 1296 \end {align}$$

بنابراین، جواب این مثال $$1296$$ است.

مثال دهم اتحاد مربع‌

با استفاده از اتحاد اول و دوم، تساوی زیر را اثبات کنید.

$$\large ( x - y ) ^ 2 + ( x + y ) ^ 2 = 2 ( x ^ 2 + y ^ 2 )$$

حل: از دو اتحاد زیر استفاده می‌کنیم:

$$\large ( x - y ) ^ 2 = x ^ 2 - 2 x y + y ^ 2$$

$$\large ( x + y ) ^ 2 = x ^ 2 + 2 x y + y ^ 2$$

در نتیجه، خواهیم داشت:

$$ \large \require {cancel} \begin {align*} ( x - y ) ^ 2 + ( x+ y ) ^ 2 & = x ^ 2 \cancel {- 2 x y} + y ^ 2 + x ^ 2 + \cancel { 2 x y } + y ^ 2\\ & = 2 x ^ 2 + 2 y ^ 2 = 2 ( x ^ 2 + y ^ 2 ) \end {align*} $$

مثال یازدهم اتحاد مربع‌

با استفاده از اتحاد مربع، مقدار عددی $$110^ 2$$ را محاسبه کنید.

حل: این عدد را می‌توان با استفاده از اتحاد جمع دوجمله‌ای یا همان اتحاد مربع به صورت زیر نوشت و محاسبه کرد:

$$\large \begin {align*} ( 110 ) ^ 2 & = ( 100 + 10 ) ^ 2 = 100 ^ 2 + 2 ( 100 ) ( 10 ) + 10^ 2 \\ & = 10000+2000+ 100 = 12100 \end {align*}$$

مثال دوازدهم اتحاد مربع‌‌

اگر $$x + y = 10$$ و $$x y = 5$$ باشد، حاصل $$x ^ 2 + y ^ 2$$ را به دست آورید.

حل: اتحاد مربع به‌صورت زیر است:

$$\large ( x + y ) ^ 2 = x ^2 + 2 x y + y ^ 2$$

طبق این رابطه، می‌توانیم تساوی زیر را بنویسیم:

$$\large x ^ 2 + y ^ 2 = ( x + y ) ^ 2 - 2 x y$$

بنابراین، مقدار مورد نظر این‌گونه به‌دست می‌آید:

$$\large x ^ 2 + y ^ 2 = ( 10) ^ 2 - 2 ( 5 ) = 100 -10 = 90$$

مثال سیزدهم اتحاد مربع‌‌‌

اگر $$x + \frac 1 x = 5$$ باشد، آنگاه مقدار عبارت $$x ^ 4 + \frac {1} { x ^ 4 }$$ را به‌دست آورید.

حل: اتحاد مربع زیر را برای دو جمله $$x$$ و $$\frac 1 x$$ داریم:

$$\large ( x + \frac 1 x ) ^ 2 = x ^ 2 + 2 ( x ) ( \frac 1 x ) + (\frac 1 x ) ^ 2 = x ^ 2 +2 + \frac 1 { x ^ 2 } = x ^ 2 + \frac 1 { x ^ 2 } + 2$$

مقدار $$x + \frac 1 x = 5$$ را می‌دانیم و در تساوی بالا قرار می‌دهیم. بنابراین، خواهیم داشت:

$$\large ( 5) ^ 2 = 25 = x ^ 2 + \frac 1 { x ^ 2 } + 2$$

بنابراین، تساوی زیر را داریم:

$$\large x ^ 2 + \frac 1 { x ^ 2 } = 23$$

اکنون دو طرف تساوی بالا را به توان دو می‌رسانیم و می‌نویسیم:

$$\large \left ( x ^ 2 + \frac 1 { x ^ 2 } = 23 \right ) ^ 2 \Rightarrow \left ( x ^ 2 + \frac 1 { x ^ 2 } \right )^ 2 = 23 ^ 2$$

با به توان دو رساندن عبارت سمت چپ، داریم:

$$\large (x ^ 2)^ 2 + 2 ( x ^ 2 ) ( \frac 1 { x ^ 2 } ) + ( \frac 1 { x ^ 2 } ) ^ 2 = 529 \\ \large \Rightarrow x ^ 4 + 2 + \frac 1 { x ^ 4 } = 529 \\ \large \Rightarrow x ^ 4 + \frac 1 { x ^ 4 } = 529 - 2 = 527$$

معرفی فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی

یکی از آموزش‌های ویدیویی دوره دبیرستان فرادرس، «آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی» است که به طور ویژه مربوط به دانش‌آموزان رشته علوم انسانی است. این آموزش ویدیویی در قالب چهار درس و در زمان ۶ ساعت و ۱۹ دقیقه تدوین شده است. در درس یکم، معادله درجه دوم مورد بحث قرار گرفته که شامل مطالب اصلی درس، نکات مهم و مثال‌های حل شده است. در درس دوم، موضوع مهم تابع ارائه شده و در آن، به موارد مهمی از قبیل تعریف ضابطه و تابع، رسم آن، دامنه و برد تابع و... پرداخته شده است. کار با داده‌های آماری موضوع درس سوم است. در نهایت، در درس چهارم به طور کامل، مطالب کتاب درسی درباره نمایش داده‌ها ارائه شده است.

• برای مشاهده فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی + اینجا کلیک کنید.

جمع‌بندی

در این مثال، با اتحاد مربع دوجمله‌ای و سه‌جمله‌ای آشنا شدیم. همچنین، اثبات آن‌ها را بیان کردیم. در پایان نیز مثال‌های متنوعی را از کاربرد این اتحاد حل کردیم.