تتریشن (Tetration) یا هایپر-۴ (hyper-4) — به زبان ساده
در ریاضیات تتریشن یا هایپر-۴ به عبارتی نمایی گفته میشود که بهصورت برگشتی و تکراری محاسبه میشود. تتریشن نوعی «اَبَر عمل» (Hyperoperation) بین «توان» (Exponentiation) و Pentation محسوب میشود. کلمه تتریشن یا tetration از دو بخش تترا یا همان ۴ و «تکرار» (Iteration) تشکیل شده است.
تتریشن
برای هر عدد مثبت ($$ a > 0 $$) و مقادیر صحیحِ غیرصفر $$ n $$، میتوان عبارتی دو ضابطهای را به صورت زیر تعریف کرد.
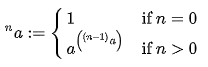
عبارت فوق معادل با به توان رساندن یک عدد طبیعی، به صورت تکراری است. توجه داشته باشید که دو عبارتِ $$ {\displaystyle \,\!{^{n}a}} \,\! $$ و $$ a ^ n $$ مفاهیم متفاوتی را نشان میدهند. برای نمونه به ازای مقادیر ارائه شده برای $$ a $$ و $$ n $$، اعداد زیر بدست میآیند.
$$ \large a = 2 , n = 3 $$
$$ \large { { ^ { 3 } 2 } } \, = 16 \ \ , \ \ 2 ^ 3 = 8 $$
ویژگیها
تتریشن دارای ویژگیهایی است که اکثر آنها مشابه با توابع توانی هستند. با توجه به اینکه توان از خاصیت جابجایی پیروی نمیکند، بنابراین نمیتوان گفت الزاما دو رابطه زیر برای تتریشن برقرار هستند (در مواردی ممکن است این روابط برقرار باشند).
$$ \large { \textstyle { } ^ { a } \left ( { } ^ {b } x \right ) = \left ( { } ^{ a b }x \right ) } $$
$$ \large { \textstyle { } ^ { a } \left ( x y \right ) = { } ^ { a }x { } ^ { a } y } $$
البته در مسائل مبتنی بر اثبات، میتوان از ویژگی زیر نیز برای تتریشن استفاده کرد.
$$ \large {\textstyle {} ^ { a } x= x ^ { \left ( { } ^ {a - 1 } x \right ) } } $$
بینهایت
همانطور که احتمالا متوجه شدهاید تفاوت تتریشن با به توان رساندن عادی، در ترتیب محاسبه توان است. در حقیقت در توان عادی، در ابتدا پایهها محاسبه شده، سپس پایه بدست آمده به توان میرسد. اما در تتریشن در ابتدا توان محاسبه شده، پس از آن پایه به توان بدست آمده خواهد رسید. حال تابعی را به صورت زیر در نظر بگیرید.
$$ \large y = { } ^ { n } x $$
بدیهی است که تابع فوق به ازای n=1 به صورت یک خط است. حال با افزایش مقادیر $$ n $$، شکل آن نیز تغییر میکند. اما سوال این است که آیا توانهای $$ x $$، به صورت خطی تغییر میکنند؟
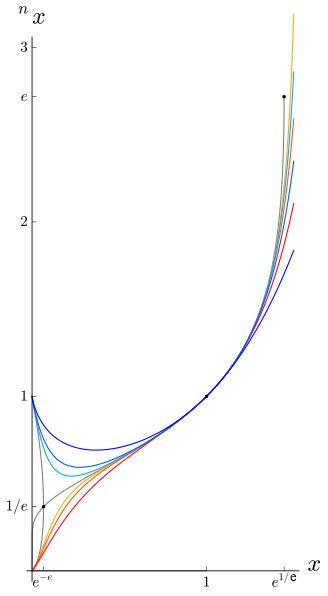
$$ \large \begin {gather*} { } ^ { 1 } x = x \\ { } ^ { 2 } x = x ^ { x ^ x } \\ { } ^ { 3 } x = x ^ { x ^ { x ^ x } } \\ ... \\ { } ^ { n } x = x ^ { \underbrace { x^ { x ^ { . . .} } } _ n \text {}} \end {gather*} $$
همانطور که مشاهده میکنید اختلاف بین مرتبه منحنیهای بدست آمده، خطی تغییر نمیکنند. حال فرض کنید در تابع در نظر گرفته شده، مقدار $$ n $$ را به بینهایت میل دهیم.
$$ \large y = \textstyle \lim _ { n \rightarrow \infty } { } ^ { n } x $$
میتوان این سوال را مطرح کرد که به ازای چه مقادیری از $$ x $$، مقدار تابع به بینهایت میل میکند؟ شاید در ابتدا تصور کنید که به ازای هر عددی بیشتر از ۱ حد فوق بینهایت میشود. اما «لئونارد اویلر» (Leonhard Euler)، ریاضیدان سوییسی نشان داد که حاصل حد فوق در بازهای مشخص، همگرا است. جالب است بدانید که بخشی از این بازه در اعداد بیشتر از ۱ قرار دارد. این بازه برابر است با:
$$ \large {\displaystyle \textstyle \left ( e ^ { - 1 } \right ) ^ { e} \leq x \leq e ^ { \left ( e^ { - 1 } \right ) } } $$
شاید این سوال را در ذهن داشته باشید که بازه فوق به چه صورت بدست آمده است. بدین منظور در ابتدا از طرفین عبارت $$ y = x ^{ x ^ {x ^ { ...} } } $$ لگاریتم طبیعی میگیریم. در این صورت داریم:
$$ \large \ln y = x ^ { x ^ {x ^ { ...} } } \ln x $$
همانطور که میبینید با گرفتن لگاریتم از تابع $$ y $$، ترم تتریشن در معادله ظاهر میشود. در حقیقت معادله فوق را میتوان به صورت زیر بازنویسی کرد.
$$ \large \ln y = y \ln x \Rightarrow y = x ^ y \Rightarrow y ^ { \frac { 1 } { y } } = x $$
بنابراین مقادیر قابل قبول برای $$ x $$، معادل با ماکزیمم و مینیمم عبارت $$ y ^ { \frac { 1 } { y } } $$ است. ماکزیمم مقدار این عبارت برابر با $$ e ^ { \frac { 1 } { e } } $$ و مینیمم مقدار آن نیز برابر با $$ e ^ { - e } $$ است. نمودار زیر مقدار حد فوق را به ازای مقادیر مختلف $$ x $$ نشان میدهد.
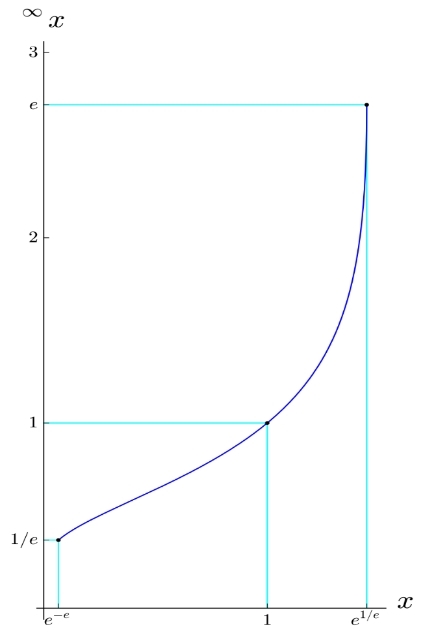
همانطور که در نمودار فوق نیز نشان داده شده، خروجی تابع نیز در بازه $$ \frac { 1 } { e } $$ تا $$ e $$ قرار میگیرد. حال فرض کنید میخواهیم معادلهای به صورت زیر را حل کنیم.
$$ \large a = x ^{ x ^ { x ^ {^ { ...} } } } $$
در این صورت معادله فوق برای مقادیری از $$ a $$ پاسخ دارد که در بازه $$ \frac { 1 } { e } $$ تا $$ e $$ قرار گرفته باشند. همچنین مقدار بدست آمده برای $$ x $$ نیز باید در بازه $$ \large {\displaystyle \textstyle \left ( e ^ { - 1 } \right ) ^ { e} \leq x \leq e ^ { \left ( e^ { - 1 } \right ) } } $$ قرار داشته باشد.
مثال
پاسخ معادله $$ 5 = x ^ { x ^ { x ^ { ^ { ... } } } } $$ را بیابید.
در اثباتی که به منظور بدست آوردن دامنه $$ x $$ در بالا انجام شد، $$ x $$ را مطابق با رابطه زیر بر حسب $$ y $$ بدست آوردیم.
$$ \large y ^ { \frac { 1 } { y } } = x $$
بنابراین در اولین نگاه بهنظر میرسد پاسخ معادله برابر با $$ x = 5 ^ { \frac { 1 } { 5 } } $$ است. اما توجه داشته باشید که عدد سمت راست باید در بازه بین $$ \frac { 1 } { e } $$ تا $$ e $$ قرار داشته باشد. بدیهی است که $$ 5 $$ خارج از این بازه قرار دارد، بنابراین این معادله پاسخی گویا ندارد. جالب است بدانید که اگر این تابع در فضای مختلط نیز تعریف شود، معادله پاسخی خارج از این بازه نخواهد داشت. در ادامه تقریب تتریشن در فضای مختلط و صفحه مربوط به آن ارائه شدهاند.
$$ \large { \displaystyle { } ^ { \infty } z = z ^ { z ^ { \cdot ^ { \cdot ^ { \cdot } } } } = { \frac { \mathrm { W } (-\ln { z } ) } { - \ln { z } } } ~ } $$
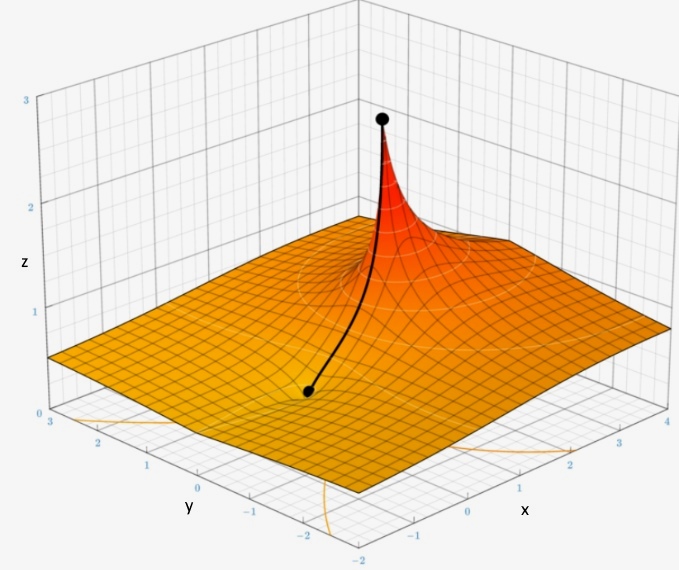
در نهایت میتوان گفت، اگر عددی همچون $$ a $$ به جای $$ 5 $$ قرار گیرد، زمانی معادله، پاسخی گویا خواهد داشت که $$ a $$ در بازه $$ \frac { 1 } { e } < a < e $$ قرار داشته باشد.
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- توابع نمایی و عدد e -- به زبان ساده
- لگاریتم و هر آنچه باید درباره آن بدانید – به زبان ساده
- بی نهایت و مفهوم آن — به زبان ساده
^^










