مدار RLC – از صفر تا صد (+ دانلود فیلم آموزش رایگان)
در مطلبی که پیشتر در بلاگ فرادرس منتشر شده، در مورد مفاهیم القا و انرژی ذخیره شده در میدان مغناطیسی القاگر بحث شد. از طرفی در بخشی دیگر مفاهیم مدار الکتریکی نیز شرح داده شد. حال زمان آن رسیده تا با معرفی کردن مفاهیم القای الکتریکی، خازن و مقاومت الکتریکی در مورد مدار RLC بحث کنیم. مدار RLC در حقیقت مداری بسته است که از مقاومت، خازن و القاگر -مثلا سولنوئید- تشکیل شده است. در این مطلب در ابتدا در مورد مدار RL و LC بحث میکنیم و نهایتا مدار RLC را معرفی خواهیم کرد.


مدارهای RL
مدار RL، سیستمی بسته است که در آن از دو جزء اصلی مقاومت و القاگر استفاده شده. مشخصهای تحت عنوان مرتبه را میتوان برای مدارهای RL تعریف کرد. این دو المان میتوانند با اتصالی موازی و یا سری در مدار قرار گیرند.
خودالقایی و قانون کیرشهف اصلاح شده
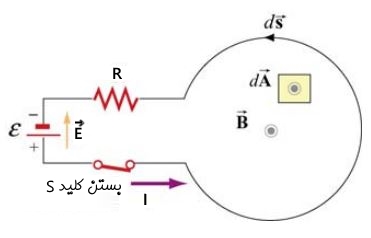
تغییر میدان مغناطیسی در یک سیکل بسته به این معنی است که انتگرال خطی میدان الکتریکی روی کل مدار غیرصفر است. جهت بررسی بیشتر، مطابق با شکل زیر مداری را در نظر بگیرید که از یک مقاومت الکتریکی و یک حلقه رسانا تشکیل شده و کل سیستم به منبعی الکتریکی متصل شده است.
انتگرال میدان الکتریکی روی مسیر بسته نشان داده شده برابر است با:
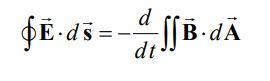
در هر مداری الکتریکی که جریان در آن با زمان تغییر میکند، میدان مغناطیسی نیز نسبت به زمان متغیر خواهد بود؛ این امر منجر به القای میدان الکتریکی در کل مدار خواهد شد. بنابراین این سوال پیش میآید که چنین مداری را به چه شکل بایستی تحلیل کرد؟
با فرض اینکه میدان مغناطیسی در یک مدار متغیر باشد، پتانسیل الکتریکی بین دو نقطه a و b بایستی به درستی تعریف شود. در حقیقت در این حالت با توجه به اینکه انتگرال خطی میدان الکتریکی روی سطح غیرصفر است، بنابراین اختلاف پتانسیل الکتریکی بین دو نقطه، وابسته به مسیر پیموده شده از a تا b است. بهطور دقیقتر میتوان گفت که با توجه به پایسته نبودن میدان الکتریکی در این حالت، نمیتوان اختلاف پتانسیل الکتریکی را معادل منفی گرادیان میدان الکتریکی دانست.
مطابق با شکل ۱، مداری را در نظر بگیرید که از یک باتری، مقاومت، کلید S و حلقهای القاگر تشکیل شده است. تصور کنید که در لحظه t=0 کلید را بسته و در نتیجه آن جریان الکتریکی از پایه مثبت باتری به سمت پایه منفی به حرکت در میآیند. به نظر شما معادله جریان (I(t برای t>0 به چه شکل بدست میآید؟
جهت پاسخ به سوال بالا، از قانون القای فارادی استفاده میکنیم. بهمنظور استفاده از این قانون، در ابتدا بردار را به صورت عمود و به سمت بیرون از صفحه در نظر میگیریم. همچنین بردار دیفرانسیل حرکت روی حلقه و در جهت پادساعتگرد را نشان میدهد.
در ابتدا تلاش میکنیم تا انتگرال میدان الکتریکی را روی کل مدار محاسبه کنیم. مطابق با مفاهیم بیان شده در مطلب میدان الکتریکی بدیهی است که جهت آن در داخل باتری از سمت پایه مثبت به سمت پایه منفی باتری است. این در حالی است که جهت بردار از سمت پایه منفی به سمت پایه مثبت است. در نتیجه حاصلضرب داخلی میدان الکتریکی در این بردار -در داخل باتری- کمتر از صفر خواهد بود. از این رو با فرض اینکه نیروی محرکه باتری برابر با باشد، انتگرال میدان درون باتری برابر است با:
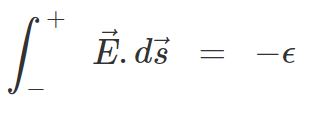
در مقاومت نیز میدانی الکتریکی وجود دارد که در جهت جریان الکتریکی است. در نتیجه حاصلضرب داخلی بردار میدان الکتریکی در جابجایی بیشتر از صفر خواهد بود. به نظر شما در هنگام عبور از حلقه چه اتفاقی خواهد افتاد؟ اگر مقاومت الکتریکی حلقه ناچیز فرض شود، تغییرات میدان الکتریکی نیز در آن صفر خواهد بود. در نتیجه انتگرال روی مسیر بسته مفروض را میتوان به شکل زیر نوشت:
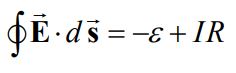
پس از تحلیل میدان الکتریکی، زمان آن فرا رسیده تا شار مغناطیسی را روی سطح بسته بیابیم. در ابتدا فرض میکنیم که بخشی از مدار که باتری، مقاومت و کلید در آن قرار گرفته، سهم اندکی را در شار مغناطیسی دارند [این فرض به دلیل کم بودن مساحت این بخشها نسبت به حلقه دایرهای است].
نکته دوم این است که با توجه به پادساعتگرد بودن جریان الکتریکی در سیم، میدان مغناطیسی و بردار هر دو به سمت بیرون صفحه هستند. در نتیجه حاصل ضرب داخلی آنها نیز مثبت هستند ().
با توجه به مفاهیم بیان شده در مطلب القای الکتریکی، شار مغناطیسی عبوری از سطح حلقه برابر با \Phi_B=LI است. در این رابطه L بهعنوان ضریب خودالقایی مدار در نظر گرفته شده که به هندسه مدار مرتبط است. تغییرات زمانی شار مغناطیسی متناسب با (L (dI/dt است. در نتیجه قانون القای فارادی را میتوان به شکل زیر بازنویسی کرد:
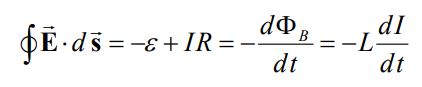
رابطه بالا بر حسب اختلاف پتانیسل، به صورت زیر قابل ارائه است.
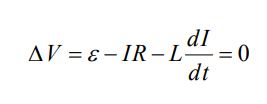
عبارت بالا در حقیقت بیان قانون کیر-شهف در حالتی است که جریان الکتریکی با زمان تغییر میکند. شماتیک زیر استفاده از این قانون را در یک نگاه توصیف میکند.
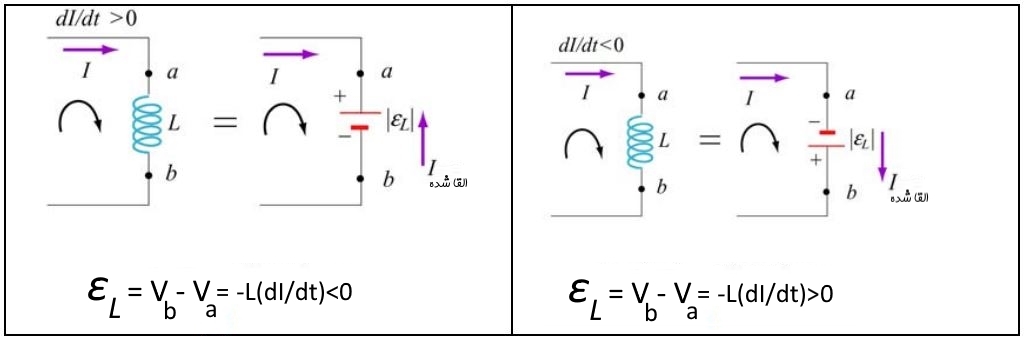
مطابق با تصویر بالا تفاوت قانون کیر شهف در این حالت، استفاده از قانون لنز است. در حقیقت با افزایش زمانی جریان الکتریکی، نیروی محرکه القا شده در خلاف جهت جریان و با کاهش زمانیِ جریان الکتریکی، نیروی محرکه القا شده در جهت جریان الکتریکی است. بنابراین القاگر را میتوان با استفاده از یک باتری جایگزین کرد. جهت قطب مثبت و منفی باتری مذکور نیز با استفاده از قانون لنز، قرار داده میشود. از طرفی اندازه نیروی محرکه این باتری برابر است با:
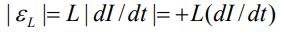
نکته بسیار مهم این است که در هر دو حالت افزایشی یا کاهشی بودن جریان الکتریکی، تغییر پتانسیل الکتریکی در زمان حرکت از نقطه a به b، برابر است با:
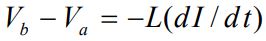
در رابطه بالا به علامت منفی و ترتیب a و b توجه داشته باشید. با استفاده از قانون کیر شهف در این حالت، میتوان مدارهای الکتریکی که شامل القاگر هستند را نیز تحلیل کرد. در ادامه چندین تحلیل در مورد تغییرات جریان الکتریکی و دیگر پارامترهای موجود انجام خواهد شد که جهت درک هرچه بهتر پیشنهاد میکنیم به آنها توجه فرمایید.
جریان افزایشی
مطابق با شکل زیر مداری RL را در نظر بگیرید. فرض کنید که در لحظه t=0 کلید بسته شده و اتصال برقرار میشود. توجه داشته باشید که جریان الکتریکی بهطور ناگهانی به مقدار ماکزیمم خود، یعنی ε / R نمیرسد. دلیل این امر وجود القاگر در مدار است.
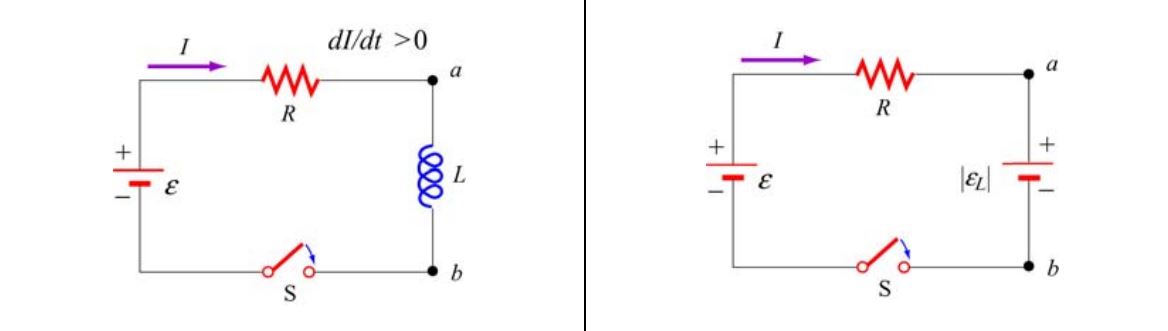
در لحظاتی که جریان الکتریکی در حال افزایش است (۰ < dI/dt)، مدار RL مفروض را میتوان با استفاده معادله دیفرانسیل زیر توصیف کرد:
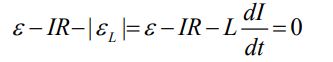
همانطور که در مطلب القای الکترومغناطیسی به تفصیل توضیح داده شد، تفاوت عمدهای میان رفتار القاگر و مقاومت الکتریکی در مدار وجود دارد. در حقیقت پتانسیل الکتریکی دو سر مقاومت، وابسته به I و اختلاف پتانسیل دو سر القاگر نیز وابسته به نرخ تغییرات جریان الکتریکی است (dI/dt).
جهت بدست آوردن تغییرات جریان الکتریکی بر حسب زمان، رابطه ۱ را به شکل زیر بازنویسی میکنیم.
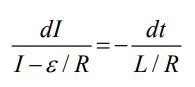
از دو طرف رابطه بالا انتگرالگیری کرده و جریان الکتریکی بهصورت زیر بدست میآید.
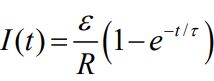
در این رابطه τ برابر است با:
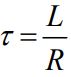
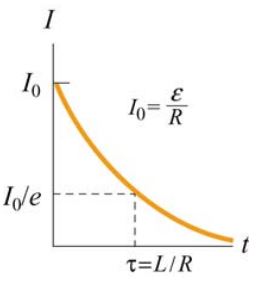
τ ثابت زمانی مدار RL است. نمودار زیر تغییرات جریان الکتریکی را بر حسب زمان نشان میدهد.
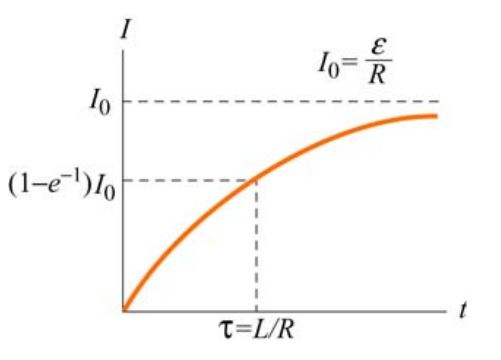
همانطور که میبینید در نمودار بالا پس از گذشت زمانی کافی، جریان الکتریکی به مقدار ثابت ε / R میل کرده است. در حقیقت، در این لحظه القاگر همچون سیمی رسانا عمل میکند. پارامتر τ معیاری از سرعت رسیدن جریان به حالت پایا است. با توجه به رابطه τ = L / R، مقادیر بزرگتر L نشان دهنده زمان مورد نیاز بزرگتر جهت رسیدن به حالت تعادل هستند. در نمودار زیر سه حالت متفاوت استفاده از L نشان داده شده. در دو حالت از آنها از القاگر استفاده شده و حالت بدون استفاده از آن نیز در این نمودار نشان داده شده.
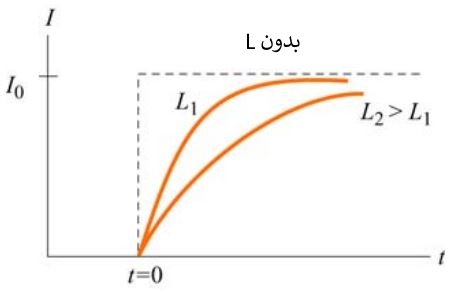
با ضرب کردن رابطه ۱ در I میتوان به معادله پایستگی انرژی دست یافت. این رابطه در زیر بیان شده است.
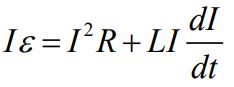
سمت چپ رابطه بالا نشان دهنده نرخ انرژی داده شده به مدار از جانب باتری است. از طرفی روابط سمت راست نیز انرژی تلف شده در مقاومت الکتریکی و نرخ انرژی ذخیره شده در القاگر را نشان میدهند.
نزول جریان
فرض کنید پس از بستن کلید، زمانی طولانی سپری میشود. همانطور که در بالا بیان شد، پس از گذشت این زمان، جریان پایا شده و مقدار آن برابر با ε / R میشود. بدیهی است که با باز کردن کلید، جریان الکتریکی طی فرآیندی به صفر خواهد رسید. اما آیا صفر شدن آن ناگهانی است؟
جهت پاسخ به سوال بالا مطابق با شکل زیر فرض کنید پس از گذشت زمانی طولانی از برقراری اتصال، کلید مدار بسته میشود.
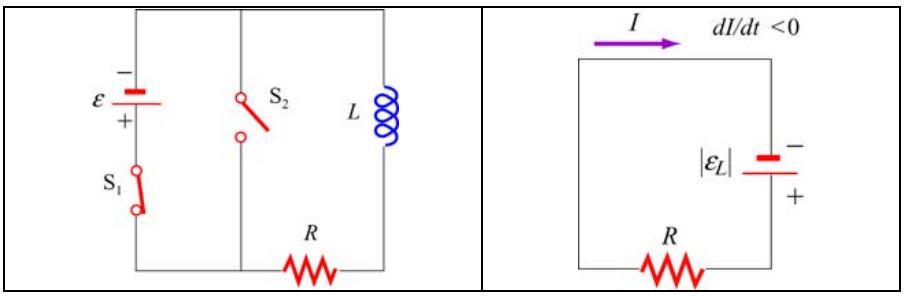
با فرض اینکه dI/dt < 0 باشد، قانون اصلاح شده کیر شهف برای این مدار به شکل زیر نوشته میشود.
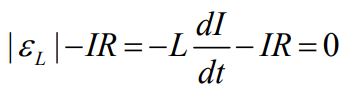
رابطه بالا بهصورت زیر قابل بازنویسی است.
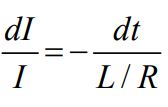
با انتگرالگیری از طرفین رابطه بالا، جریان الکتریکی برابر با تابع زیر بدست میآید.
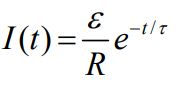
در رابطه بالا τ = L / R و برابر با ثابت بیان شده در حالتی است که کلید مدار بسته میشود. نمودار مربوط به رابطه بالا در زیر نشان داده شده.
مدار LC
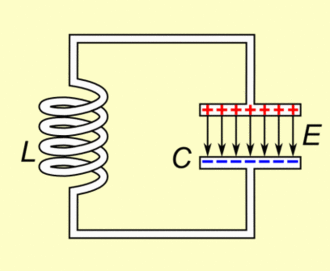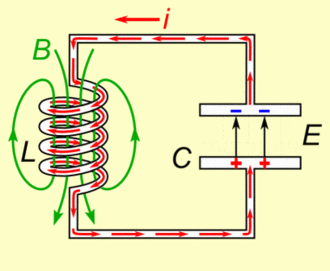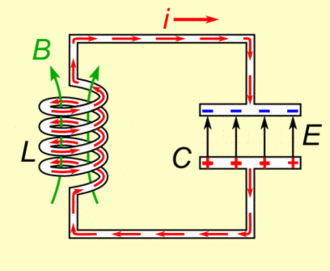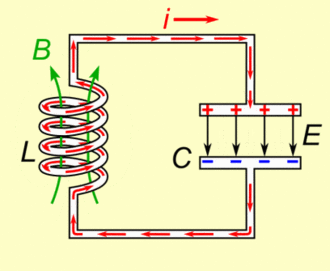
مداری LC را در نظر بگیرید که در آن از دو جزء خازن و القاگر استفاده شده است. شکل زیر مدار مذکور را نشان میدهد.
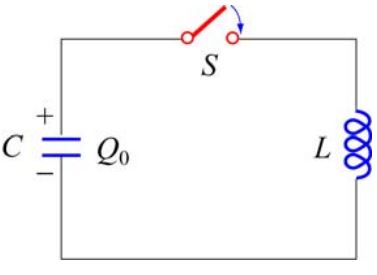
تصور کنید که خازن در حالت اولیه دارای بار Q۰ است. زمانی که کلید S بسته میشود، خازن شروع به تخلیه بار الکتریکی میکند و انرژی الکتریکی آن کاهش مییابد. از طرفی بار به جریان درآمده منجر به ایجاد میدان مغناطیسی میشود. نهایتا انرژی مغناطیسی تولید شده، در القاگر ذخیره خواهد شد.
با نادیده گرفتن مقاومت الکتریکی، انرژی کل، بصورت نوسانی به انرژی الکتریکی در خازن و انرژی مغناطیسی در القاگر تبدیل میشود. اصطلاحا به این پدیده نوسان الکترومغناطیسی گفته میشود.
انرژی کل موجود در مدار LC، پس از بستن کلید S برابر است با:
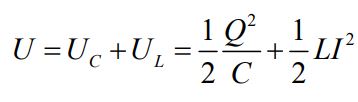
با استفاده از مفهوم ثابت بودن انرژی کل U در مدار، رابطه تعادل زیر را میتوان نوشت.
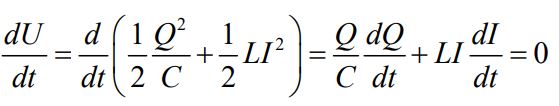
نهایتا معادله دیفرانسیل مربوط به بار الکتریکی قرار گرفته روی صفحات خازن، بصورت زیر بیان میشود.
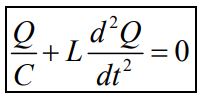
جریان الکتریکی در هر لحظه برابر با I=-dQ/dt است. در نتیجه ترم دوم رابطه بالا نرخ تغییرات جریان الکتریکی را نشان میدهد (d2Q/dt2=dI/dt-). علامت منفی استفاده شده در این رابطه نشان دهنده کاهشی بودن بار روی صفحات خازن پس از بستن کلید مدار است. رابطه بالا را میتوان بهصورت زیر بازنویسی کرد.

جهت حل معادله دیفرانسیل ارائه شده در رابطه ۲، پاسخ عمومی را برابر با معادله زیر در نظر میگیریم:
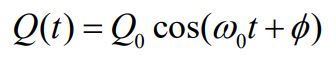
در پاسخ فرض شده بالا Q0 دامنه بار الکتریکی نوسانی و φ فاز است. با جایگذاری پاسخ بالا در رابطه ۲، فرکانس زاویهای ω0 برابر با عدد زیر بدست میآید.
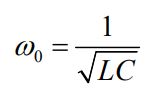
با در نظر گرفتن رابطه ۳ به عنوان بار Q، جریان الکتریکی I در هر لحظه با استفاده از مشتقگیری از آن، به شکل زیر بدست میآید.
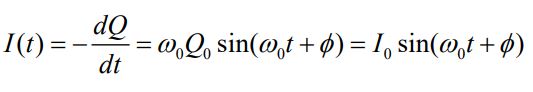
در رابطه بالا I0=ω0Q0، دامنه جریان است. از طرفی با فرض حالت اولیه Q(t=0)=Q0 و I(t=0)=0، اختلاف فاز φ برابر با φ=۰ بدست میآید. در نتیجه پاسخ نهایی جریان و بار الکتریکی برابر خواهند بود با:
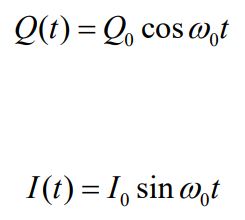
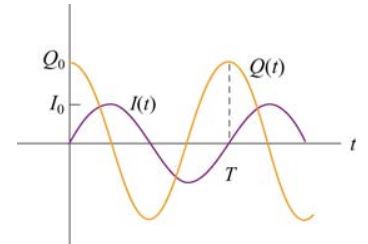
نمودار و انیمیشن زیر بار و جریان الکتریکی جابجا شده بین القاگر و خازن را نشان میدهد.
با بکارگیری دو معادله (Q(t و (I(t، انرژی الکتریکی و مغناطیسی در هر لحظه با استفاده از روابط زیر تعریف میشوند.
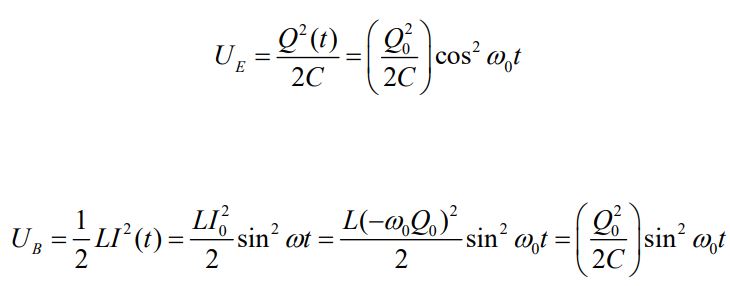
نکته جالب دو رابطه بالا این است که با جمع زدن آنها به عدد ثابتی میرسیم. در حقیقت انرژی کل سیستم در هر لحظه برابر است با:
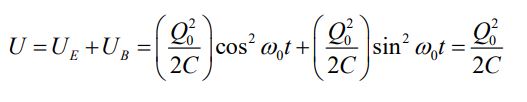
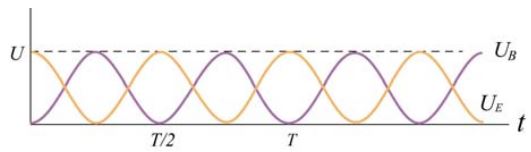
بنابراین انرژی سیستم در هر لحظه برابر با انرژی اولیه خازن (Q02/2C) است. نوسان انرژی الکتریکی و مغناطیسی در نمودار زیر نشان داده شده.
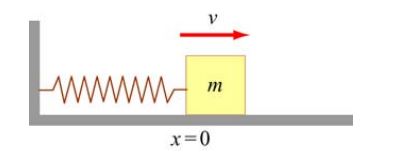
جهت معادلسازی مکانیکی مدارِ LC، میتوان از سیستم جرم-فنر نشان داده شده در شکل زیر استفاده کرد. البته در مبحث ارتعاشات مکانیکی، بهطور مفصل در مورد سیستم جرم-فنر بحث شد.
با فرض اینکه سرعت، ضریب سختی و جابجایی جرم نسبت به حالت تعادل، به ترتیب برابر با k ,v و x باشند، مجموع انرژی جنبشی و پتانسیل سیستم جرم-فنر برابر است با:
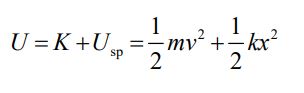
در رابطه بالا Usp و K بهترتیب برابر با انرژی پتانسیل و جنبشی جرم و فنر هستند. با مشتقگیری زمانی از رابطه بالا داریم:
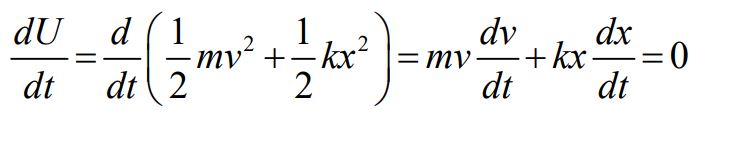
رابطه مذکور را میتوان به شکل زیر بازنویسی کرد.
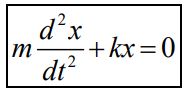
پاسخ معادله دیفرانسیل بالا برابر است با:
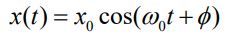
با توجه به این پاسخ، فرکانس نوسان را میتوان با استفاده از رابطه زیر توصیف کرد.
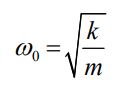
بر مبنایِ مقادیر دامنه و فرکانس طبیعی، انرژی کل سیستم جرم-فنر در هر لحظه مطابق با رابطه زیر بدست میآید.

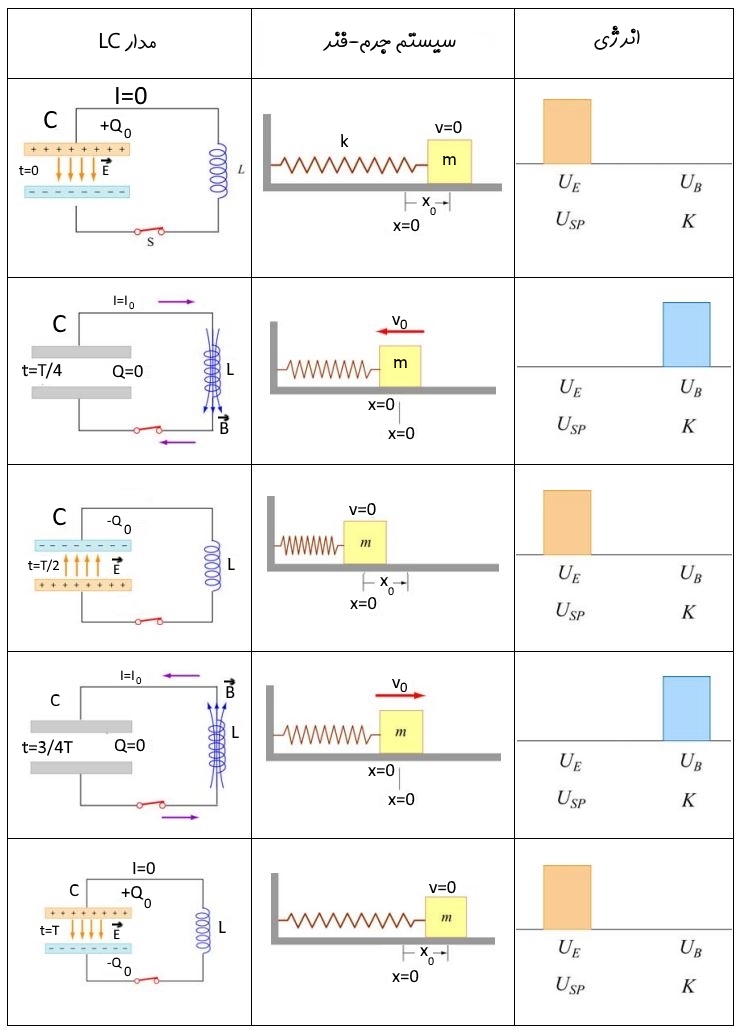
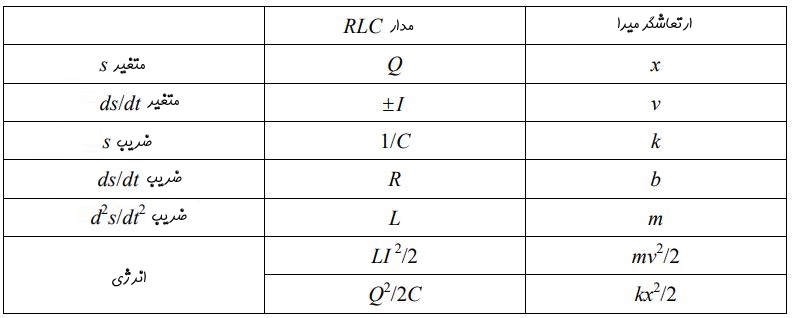
همانطور که از رابطه بالا پیدا است، انرژی کل سیستم جرم-فنر نیز ثابت است. در جدول زیر مدار LC و سیستم جرم-فنر در حالتهای مختلف مقایسه شدهاند. این جدول جهت کمک به درک مدار LC بسیار تاثیرگذار است؛ لذا مطالعه و بررسی دقیق آن شدیدا توصیه میشود.
مدار RLC
با بررسی مدارهای RL و LC، حال زمان آن فرا رسیده تا مداری را بررسی کنیم که هر سه این اجزاء در آن وجود داشته باشند. مداری مطابق با شکل زیر را در نظر بگیرید که در آن از مقاومت، القاگر و خازن استفاده شده.
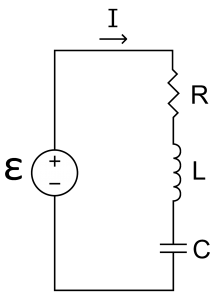
فرض کنید که بار خازن در حالت اولیه برابر با Q0 است. پس از بسته شدن کلید، بارهای الکتریکی شروع به جریان میکنند. بر خلاف مدار LC، در مدار RLC انرژی با گذشت زمان تلف شده و اندازه آن ثابت نیست. در حقیقت نرخ تلف شدن انرژی صورت گرفته در مقاومت برابر است با:
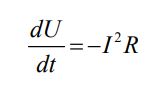
در بالا (در قسمت مدار LC) انرژی مجموع خازن و القاگر را مطابق با رابطه زیر بدست آوردیم.
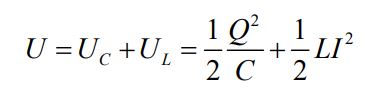
در نتیجه تغییرات انرژی ذخیره شده در القاگر و خازن برابر با انرژی تلف شده در مقاومت است. از این رو با برابر قرار دادن دو رابطه بالا داریم:
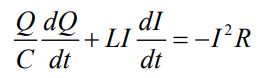
با فرض I=dQ/dt و تقسیم رابطه بالا به I، رابطه دیفرانسیل توصیف کننده مدار RLC بهشکل زیر بدست میآید.
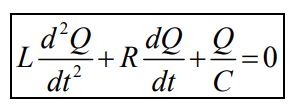
برای حالتی که R کوچک باشد، پاسخ معادله بالا برابر با رابطه زیر خواهد بود.
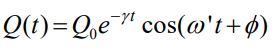
در این رابطه، γ تحت عنوان ضریب میرایی شناخته میشود و میتوان آن را با استفاده از R و L، مطابق با معادله زیر بدست آورد.

همچنین 'ω فرکانس زاویهای میرایی نامیده میشود. Q0 و φ مقادیر ثابتی هستند که از شرایط اولیه بدست میآیند.مدار RLC را میتوان معادل با سیستم جرم-فنر-دمپر در نظر گرفت. در مجموعه مطالب ارتعاشات مکانیکی به تفصیل در مورد این نوع از ارتعاشات صحبت کردیم. در ابتدا سیستم جرم-فنر-دمپری مطابق با شکل زیر را در نظر بگیرید.
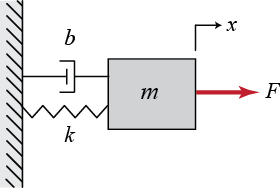
پیشتر در بلاگ فرادرس معادله نوسان سیستم جرم-فنر-دمپر فوق را مطابق با رابطه زیر توصیف کردیم.
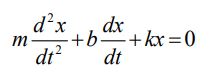
در رابطه بالا ضریب dx/dt، بخشی است که منجر به تلف شدن انرژی سیستم میشود. معادلسازی بین پارامترهای مدار RLC و سیستم جرم-فنر-دمپر در جدول زیر نشان داده شده (توجه داشته باشید که علامت جریان الکتریکی وابسته به شرایط فیزیکی حاکم بر مسئله است).
مثال ۱: مدار RL
مداری را مطابق با شکل زیر را در نظر بگیرید. جریان مقاومتها را در لحظات زیر بیابید:
- بلافاصله پس از بسته شدن کلید
- مدت زمانی طولانی پس از بسته شدن کلید

فرض کنید کلید را میبندیم و مدت زمانی طولانی منتظر میمانیم. جریان درست پس از باز شدن کلید در لحظات زیر را بیابید:
- بلافاصله پس از باز شدن کلید
- مدت زمانی طولانی پس از باز شدن کلید
روش حل
(a): درست بلافاصله پس از بسته شدن کلید، جریانی در القاگر وجود ندارد. دلیل این امر خود القایی القاگر و مانع بودن آن جهت افزایش جریانِ I3=0 است. در نتیجه با توجه به رابطه I1=I2+I3 جریان I1 و I2 در این لحظه با هم برابر هستند. شکل زیر حلقههای موجود در این مدار را نشان میدهد.
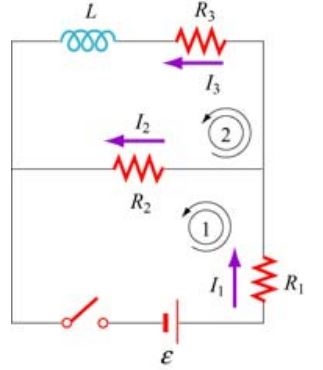
با نوشتن قانون کیر-شهف برای حلقه شماره ۱، جریانهای موجود در مقاومتها برابر با مقادیر زیر بدست میآیند.
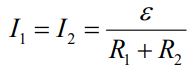
(b): پس از بسته بودن کلید برای مدت زمانی طولانی، نیروی محرکه القایی در القاگر وجود نخواهد داشت و جریان ثابت است. در این زمان، قانون حلقه برای حلقه شماره ۱ و ۲ بهترتیب برابر خواهند بود با:
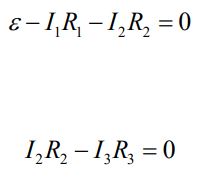
با ترکیب روابط بالا با قانون گره I1=I2+I3، جریانهای موجود در مدار برابر با مقادیر زیر بدست میآیند.

(A): بلافاصله پس از باز شدن کلید، جریان در مقاومت R1 برابر با صفر است. در نتیجه رابطه I2+I3=0 صادق است. به عبارت دیگر، حلقه شماره ۲، مداری RL را تشکیل داده و I3 شروع به کم شدن میکند. در این حالت اندازه جریانها برابر است با:
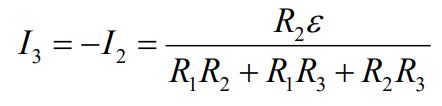
(B): پس از باز بودن کلید برای مدت زمانی طولانی، تمامی جریانها برابر با صفر خواهند بود (۰=I1=I2=I3).
مثال ۲: مدار LC
مطابق با مدار نشان داده شده در شکل زیر، فرض کنید کلید نشان داده شده برای مدت زمانی به نقطه a متصل شده و در لحظه مشخصی وضعیت آن را عوض کرده و به نقطه b متصل میکنیم.
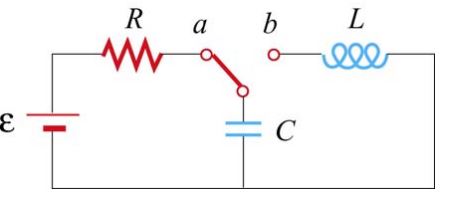
با توجه به این مدار، موارد زیر مطلوب است:
- فرکانس نوسان مدار LC
- ماکزیمم بار جمع شده روی خازن
- ماکزیمم جریان در القاگر
- انرژی کل موجود در مدار، در هر لحظه
(۱): همانگونه که در بالا نیز بیان شد، فرکانس زاویهای مدار LC برابر با است. در نتیجه فرکانس مدار مذکور برابر است با:
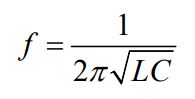
(۲): بیشترین مقدار بار الکتریکی موجود در خازن برابر است با:
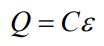
(۳): انرژی ذخیره شده در خازن برابر با مقدار زیر است.
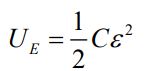
از طرفی قبلا بیان کردیم که انرژی مغناطیسی ذخیره شده در القاگر را میتوان با استفاده رابطه زیر بدست آورد.
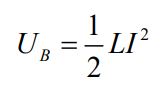
با توجه به قانون پایستگی انرژی، زمانی که جریان الکتریکی در بیشترین مقدار خود قرار دارد، کل انرژی اولیه ذخیره شده در خازن به انرژی ذخیره شده در القاگر تبدیل میشود. در حقیقت میتوان گفت:
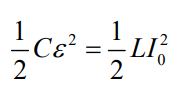
در نتیجه، بیشترین مقدار جریان الکتریکی برابر است با:
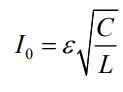
(4): در هر لحظه، کل انرژی ذخیره شده در مدار، برابر با انرژی ذخیره شده در خازن در زمان اولیه است.
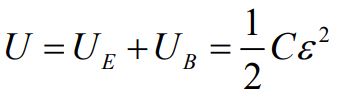
با استفاده از المانهای R ،L و C میتوان ترکیبات مختلفی از مدارهایی را ایجاد کرد که از آنها به عنوان تقویت کننده یا ذخیره کننده انرژی استفاده کرد.
در صورت علاقهمندی به مباحث مرتبط در زمینه فیزیک و مهندسی برق، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس مهندسی برق
- مجموعه آموزشهای مهندسی برق
- مجموعه آموزشهای فیزیک
- میدان مغناطیسی ناشی از سیم حامل جریان -- از صفر تا صد
- القای الکترومغناطیسی (Electromagnetic Induction) -- از صفر تا صد













سلام
در پاسخ به پیام جناب ابراهیم:
اصولاً بدلیل اینکه در ساخت سلف از سیم های مسی استفاده می شود و سیم مسی هم دارای مقاومت اهمی است با مدار LC نمی توان نوسانات سینوسی پایدار تولید کرد. برای اطلاع از چگونگی طراحی نوسانسازهای پایدار می توانید به فصل چهارم آموزش زیر مراجعه کنید:
https://faradars.org/courses/fvee96022-electronics-iii
سلام. من میخوام یه نوسان ساز با مدار RLC بسازم اما شنیدم که نوسانسازی این مدار میراست . میشه جواب بدهید که به کمک این مدار و عبور نوسان آن از یک مدار opamp عبور از صفر که تبدیل امواج به موج مربعی کامل و سپس عبور آن از یک مدار انتگراگیر و در آخر عبور آن از یک مدار RLC سری میشود یک مدار سینوسی با فرکانس f=1/(2*pi*sqrt(L*C))؟ لطفا جواب بدهید
عالی بود
خیلی مفید بود . تشکر