متغیر تصادفی، تابع احتمال و تابع توزیع احتمال

از آنجا که پیشامدها زیر مجموعه‌هایی از فضای پیشامد F در نظر گرفته می‌شوند، برای محاسبه احتمال آن‌ها باید با محاسبات روی مجموعه‌ها سروکار داشته باشیم، که البته کار ساده‌ای نیست. در عوض می‌توان به کمک تعریف «متغیر تصادفی» (Random Variable)، احتمال بسیاری از پیشامدها را براساس الگوهای احتمالی قابل دسترس، محاسبه کرد زیرا بسیاری از پدیده‌های تصادفی دارای الگوهای مشخصی هستند.

به کمک متغیر تصادفی برای هر پیشامد از فضای پیشامد یک عدد از اعداد حقیقی در نظر گرفته می‌شود. از آنجایی که پیشامدها به صورت تصادفی رخ می‌دهند، طبیعی است برای هر کدام مقداری تصادفی در نظر بگیریم. به همین علت به چنین متغیرهایی، متغیرهای تصادفی گفته می‌شود، هر چند بعدا متوجه می‌شویم که متغیرهای تصادفی در حقیقت یک تابع هستند نه متغیر!

برای آشنایی بیشتر با پیشامدها و اصول تابع احتمال بهتر است مطلب آزمایش تصادفی، پیشامد و تابع احتمال را از قبل مطالعه کرده باشید و سپس به ادامه مطالعه این مطلب بپردازید.

برای مثال فرض کنید در پرتاب دو سکه نااریب به طور مستقل فضای نمونه به صورت  $$\Omega=\{HH,HT,TH,TT\}$$ نوشته شده باشد. اگر متغیر تصادفی X را تعداد شیرها در نظر بگیریم خواهیم داشت:

$$X(\{HT\})=X(\{TH\})=1,\;\;X(\{TT\})=0,\;\;X(\{HH\})=2$$

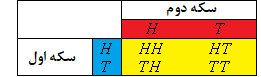
از آنجایی باید برای فضای پیشامد که مجموعه‌ای از زیر مجموعه‌های $$\Omega$$ است، احتمال محاسبه شود، می‌توانیم به صورت زیر بنویسیم:

$$P(X=1)=P({\{HT,TH}\})=\dfrac{2}{4}=0.5$$

$$P(X=2)=P(\{HH\})=P(\{TT\})=\dfrac{1}{4}=0.25$$

$$P(X=4)=P(X<0)=P(1$$

همانطور که دیده شد، احتمال برای متغیر تصادفی را در حالت‌هایی که پیشامد مجموعه تهی باشد، برابر با صفر در نظر گرفتیم. به این ترتیب احتمال اینکه متغیر تصادفی برابر با هر مقدار یا فاصله‌ای از اعداد حقیقی باشد، بدست آمد. حال به تعریف رسمی متغیر تصادفی می‌پردازیم.

تعریف متغیر تصادفی

فرض کنید در یک آزمایش تصادفی با فضای نمونه $$\Omega$$ و فضای پیشامدهای $$F$$، هر پیشامد ساده را با $$\omega$$ نشان دهیم. بنابراین اگر X را یک عدد حقیقی برای پیشامد $$\omega$$ در نظر بگیریم، می‌نویسیم $$X(\omega)\in R$$‌ که منظور از R مجموعه اعداد حقیقی است.

حال X را متغیر تصادفی می‌نامیم، اگر برای هر فاصله‌ای از اعداد حقیقی مثل ‌‌B، بتوانیم نشان دهیم که $$X(\omega)\in B$$ قابل تبدیل شدن به یک پیشامد است، یعنی به فضای پیشامد تعلق دارد.

به بیان دقیق‌تر اگر هر مجموعه مثل B از زیر مجموعه‌های اعداد حقیقی را در نظر بگیریم، حتما $$X^{-1}(B)=\{\omega | X(\omega)\in B\}$$ باید یک پیشامد باشد و به F تعلق داشته باشد. به بیان دیگر، اگر $$X^{-1}$$ را معکوس عملیاتی که X انجام می‌داد در نظر بگیریم، برای هر مجموعه بورل از اعداد حقیقی، بتوانیم یک پیشامد در فضای پیشامد پیدا کنیم که توسط X به یک زیر مجموعه از اعداد حقیقی (مثل B) تبدیل شده باشد. منظور از «مجموعه بورل» (Borel Set)، زیرمجموعه‌ای از اعداد حقیقی است که به صورت فاصله‌های باز (a,b) قابل نمایش هستند.

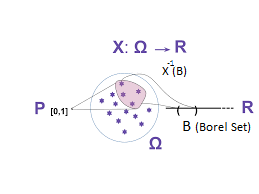
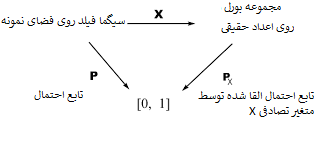
پس همانطور که دیده می‌شود، متغیر تصادفی X در حقیقت تابعی است از فضای پیشامد به مجموعه‌ای از زیرمجموعه‌های اعداد حقیقی. این عبارت را به زبان ریاضیات به صورت زیر می‌نویسیم.

$$(\Omega,F,P) \xrightarrow {X} (R,B,P_x)$$

به این معنی که متغیر تصادفی X، اعضای فضای نمونه را به اعداد حقیقی، اعضای فضای پیشامد را به مجموعه بورل B از اعداد حقیقی و تابع احتمال مربوط به پیشامد را به احتمال متغیر تصادفی تبدیل می‌کند.

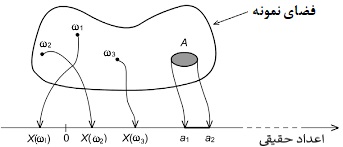
فضای احتمال القا شده توسط متغیر تصادفی

همانطور که در نمادهای بالا دیده شد، فضای احتمال برمبنای پیشامدها (P) تبدیل به فضای احتمال برمبنای متغیر تصادفی X به صورت $$P_x$$ شد. برای این که بتوان $$P_x$$ را یک تابع احتمال نامید، باید در اصول احتمال که به اصول کولموگروف معروف است، صدق کند. به منظور آگاهی و اطلاع از اصول احتمال می‌توانید مطلب آزمایش تصادفی، پیشامد و تابع احتمال را مطالعه کنید.

در ادامه به بررسی این اصول برای احتمال القا شده توسط متغیر تصادفی X می‌پردازیم.

۱- مقدار احتمال برای متغیر تصادفی X برای هر مجموعه بورل B‌، نامنفی است. با توجه به تعریف متغیر تصادفی می‌توانیم بنویسیم:

$$P_X(B)=P(X^{-1}(B))\geq 0$$

۲- مقدار احتمال برای مجموعه اعداد حقیقی (R) برابر با ۱ است. درست به مانند حالت قبل می‌توان نوشت:

$$P_X(R)=P(X^{-1}(R))=P(\Omega)=1$$

۳- احتمال تعلق متغیر تصادفی X که به اجتماعی از دنباله‌هایی از فاصله‌های اعداد حقیقی دو به دو مجزا (مجموعه‌های بورل)، برابر است با مجموع احتمالات تعلق متغیر تصادفی X به هر یک از آن‌ها. اگر $$\{B_i\}_{i=1}^\infty$$ یک دنباله از مجموعه‌های بورل دو به دو ناسازگار باشد، خواهیم داشت:

$$P_X(\cup_{i=1}^\infty B_i)=P(X^{-1}(\cup_{i=1}^\infty B_i))=P(\cup_{i=1}^\infty X^{-1}(B_i))=$$

$$\sum_{i=1}^\infty P(X^{-1}(B_i))=\sum_{i=1}^\infty P_X(B_i)$$

در نتیجه تابع احتمال القا شده توسط متغیر تصادفی X، یک تابع احتمال است.

مثال ۱

اگر X تعداد شیرهای مشاهده شده در دو بار پرتاب سکه باشد، تابع احتمال القا شده توسط X برای همه زیر مجموعه‌های اعداد حقیقی با استفاده از محاسبه احتمال پیشامدها در جدول زیر نوشته شده است.

از آنجایی که هر مجموعه بورل فقط در یکی از سطرهای جدول صادق است (مجموعه‌های بورل دو به دو ناسازگارند)، در نتیجه همه احتمالات در جدول بالا وجود دارند. در این جا لازم است که مفهوم تکیه‌گاه برای متغیر تصادفی مشخص شود.

«تکیه‌گاه» (Support) مجموعه مقدارهایی است که متغیر تصادفی با احتمال مثبت اختیار می‌کند. معمولا برای نشان دادن تابع احتمال برای متغیر تصادفی X کافی است، مقدار احتمال را برای تکیه‌گاه متغیر تصادفی مشخص کرده و برای بقیه نقاط در مجموعه اعداد حقیقی مقدار صفر را در نظر گرفت.

تابع توزیع احتمال متغیر تصادفی (Random Variable Distribution Function)

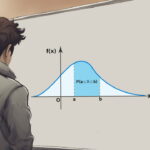
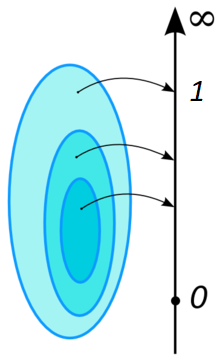
اگر X یک متغیر تصادفی باشد، تابع توزیع احتمال متغیر تصادفی X، تابعی است که اعداد حقیقی را به فاصله ۰ تا ۱ می‌برد. بنابراین تابع توزیع احتمال را به صورت زیر تعریف می‌کنیم:

$$F_X(y)=P(X\leq y);\;\;\; y \in R$$

توجه داشته باشید که منظور از $$F_X(y)$$ مقدار تابع توزیع متغیر تصادفی X در مقادیر کوچک‌تر از y است. به این ترتیب، این تابع، مقدار احتمال برای متغیر تصادفی X را تا نقطه y بیان می‌کند. به تابع توزیع احتمال، «تابع احتمال تجمعی» (Cumulative Distribution Function)  نیز گفته می‌شود. برای آشنایی با شیوه محاسبه تابع توزیع به مثال ۲ مراجعه کنید.

خصوصیات تابع توزیع احتمال متغیر تصادفی

با توجه به تعریف و نمودار مربوط به مثال ۲ مشخص است که برد تابع توزیع احتمال متغیر تصادفی از $$-\infty$$‌ تا $$+\infty$$ تعریف شده است. در ادامه به خصوصیات تابع توزیع احتمال متغیر تصادفی می‌پردازیم.

• تابع توزیع احتمال یک تابع غیر نزولی است. یعنی اگر $$y_1$$ آنگاه $$F_X(y_1)\leq F_X(y_2)$$.
• مقدار تابع توزیع احتمال برای کران بالا برابر با ۱ و برای کران پایین برابر با صفر است. یعنی $$F_X(-\infty)=0$$ و $$F_X(+\infty)=1$$.
• تابع توزیع احتمال متغیر تصادفی از راست پیوسته است. به این ترتیب اگر$$F_X(y^+)$$ را حد راست تابع توزیع احتمال در نقطه y بنامیم، آنگاه:

$$\lim_{y\to y^+}F_X(y)=F_X(y^+)=F_X(y)$$

• دو متغیر تصادفی $$X_1$$ و $$X_2$$ را هم توزیع می‌گویند اگر برای هر $$y \in R$$ داشته باشیم؛ $$F_{X_1}(y)=F_{X_2}(y)$$

• برای تابع توزیع احتمال متغیر تصادفی X می‌توان نوشت:

$$P(X=y)=F(y)-F(y^-)$$

• همچنین برای پیدا کردن مقدار احتمال می‌توان از تابع توزیع و قواعد زیر استفاده کرد:

$$P(y_1< X)=1-F_X(y_1)$$

$$P(y_1< X\leq y_2)=F_X(y_2)-F_X(y_1)$$

$$P(y_1\leq X \leq y_2)=F_X(y_2)-F_X(y_1^-)$$

$$P(y_1 \leq X$$

$$P(y_1 < X < y_2)=F_X(y_2^-)-F_X(y_1)$$

 برای آگاهی از شیوه محاسبات احتمال، براساس تابع توزیع احتمال می‌توانید به مثال 2 یا مثال 3 مراجعه کنید.

متغیر تصادفی گسسته (Discrete Random Variable)

با توجه به نوع مقدارهای تکیه‌گاه متغیر تصادفی، آن‌ها را طبقه‌بندی می‌کنند. اگر تکیه‌گاه متغیر تصادفی X، مجموعه‌ای «متناهی» (Finite) یا «نامتناهی شمارا» (Infinite- Countable) باشد،‌ آن را «گسسته» (Discreet) می‌نامند. البته مشخص است که برای هر فضای نمونه متناهی یا نامتناهی شمارا، حتما متغیر تصادفی تعریف شده، گسسته است. ولی عکس این موضوع درست نیست. زیرا برای بعضی از متغیرهای تصادفی با تکیه‌گاه متناهی لزوما یک فضای نمونه‌ متناهی یا نامتناهی شمارا نمی‌توان تصور کرد.

فیلم آموزش فرایندهای تصادفی یا اتفاقی Stochastic Processes در فرادرس

کلیک کنید

مثلاً متغیر تصادفی «نشانگر» (Indicator) با تکیه‌گاه $$S=\{0,1\}$$ به صورت زیر تعریف می‌شود. با توجه به فضای نمونه $$\Omega$$ و فضای پیشامد F تابع $$I_A$$ یک متغیر تصادفی است اگر به صورت زیر نوشته شود:

$$I_A(\omega)=1 ,\;\; \omega \in A\;\;\;\;\;\;\; I_A(\omega)=0,\;\; \omega \notin A$$

اگر فضای نمونه نامتناهی باشد، باز هم متغیر تصادفی نشانگر قابل تعریف است.

همچنین متغیر تصادفی ثابت (تباهیده) با تکیه‌گاه $$S=\{c\}$$ به صورت زیر تعریف می‌شود:

$$X(\omega)=C ,\;\; \forall \omega \in \Omega$$

این دو متغیر تصادفی نشان می‌دهند که برای یک متغیر تصادفی با تکیه‌گاه متناهی، می‌توان یک فضای نمونه نامتناهی در نظر گرفت.

متغیرهای تصادفی برنولی، دو جمله‌ای، هندسی، پواسن و فوق‌ هندسی از جمله‌ متغیرهای تصادفی گسسته هستند.

تابع احتمال متغیر تصادفی گسسته

اگر X یک متغیر تصادفی گسسته باشد، تابع احتمال آن را با $$f_X(y)$$ نشان می‌دهیم و به صورت زیر محاسبه می‌کنیم.

$$f_X(y)=P(X=y),\;\;\;y \in R$$

بنابراین باید تابع احتمال برای متغیر تصادفی گسسته برای همه مقدارهای y در اعداد حقیقی تعریف شود. در مثال ۱ تابع احتمال را می‌توان به فرم زیر نوشت:

$$f_X(y)=P(X=y)=\begin{cases} \dfrac{1}{4},\;\;\;y=0\\ \dfrac{1}{2},\;\;y=1\\ \dfrac{1}{4},\;\;y=۲\\ 0,\;\;\;\;\; elsewhere \end{cases}$$

منظور از elsewhere نقاط دیگر از اعداد حقیقی است که در تکیه‌گاه متغیر تصادفی قرار ندارند.

تابع توزیع احتمال متغیر تصادفی گسسته

با توجه به تعریف تابع توزیع متغیر تصادفی، واضح است که تابع توزیع متغیر تصادفی گسسته را می‌توان به صورت زیر محاسبه کرد.

$$F_X(y)=P(X\leq y)=\sum_{t\leq y}P(X=t)$$

مثال ۲

با توجه به اطلاعات مربوط به مثال ۱ می‌توان تابع توزیع متغیر تصادفی تعداد شیرهای دو بار پرتاب سکه را محاسبه کرد. عملیات در زیر دیده می‌شود.

$$F_X(y)=P(X\leq y)=\sum_{t\leq y}P(X=t)=\begin{cases} ۰\;\;\;\;\; y<0\\ \dfrac{1}{4},\;\;\;0\leq y<1\\ \dfrac{3}{4},\;\;\;1\leq y<2\\ 1,\;\;\;\;\;y \geq 2\\ \end{cases}$$

در نتیجه برای همه مقدارهای اعداد حقیقی تابع توزیع احتمال متغیر تصادفی X تعریف شده است. با توجه به تابع توزیع مشخص شده می‌توان به کمک قواعد محاسبه احتمال از روی تابع توزیع احتمال، محاسبات زیر را انجام داد.

$$P(X=1)=F_X(1)-F_X(۱^-)=F_X(1)-F_X(0)=\dfrac{3}{4}-\dfrac{1}{4}=\dfrac{2}{4}$$

$$P(X<2)=\dfrac{3}{4}$$

$$P(X>1)=1-P(X\leq 1)=F_X(1)=\dfrac{3}{4}$$

$$P(X<-5)=F_X(-5)=0$$

$$P(0$$

اگر تابع توزیع احتمال را برای چنین حالتی ترسیم کنیم، نموداری به صورت زیر حاصل می‌شود.

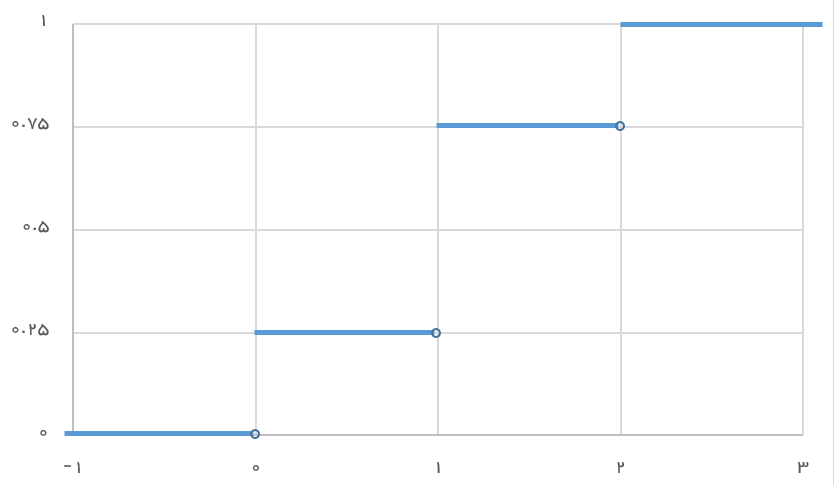
البته برای محاسبه احتمال در هر نقطه نیز می‌توان از تابع توزیع احتمال کمک گرفت. اگر بخواهیم $$P(X=y)$$ را بدست آوریم کافی است که برای هر نقطه y، محاسبه زیر را انجام دهیم.

$$P(X=y)=F_X(y)-F_X(y^-)$$

با این ترتیب مقدار احتمال در هر نقطه میزان پرش تابع توزیع احتمال در آن نقطه است. تصویر زیر نشان می‌دهد که چگونه می‌توان با استفاده از این پرش‌ها مقدار تابع احتمال را از روی تابع توزیع احتمال بدست آورد.

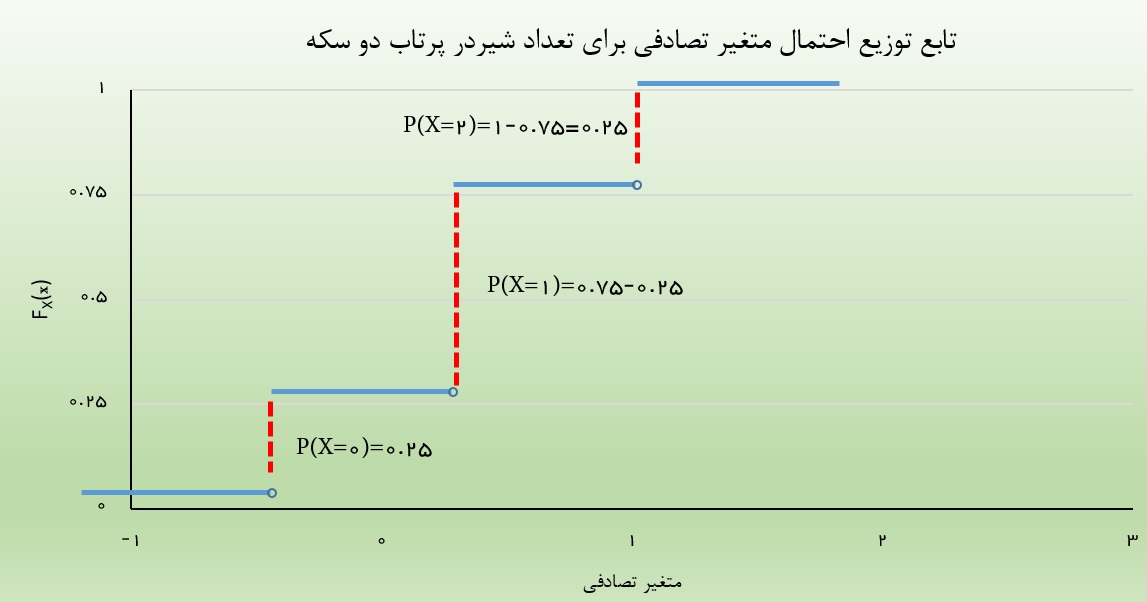
حال بد نیست نتیجه به دست آمده را با مثال ۱ مقایسه کنید.

متغیر تصادفی پیوسته (Continues Random Variable)

اگر تکیه‌گاه متغیر تصادفی X یک مجموعه «نامتناهی غیرشمارا» (Infinite - Uncountable) باشد، آن را یک متغیر تصادفی پیوسته می‌گویند. معمولا تکیه‌گاه متغیر تصادفی پیوسته به صورت یک یا اجتماعی از فاصله‌های اعداد حقیقی در نظر گرفته می‌شود.

فیلم آموزش متغیرهای تصادفی پیوسته (رایگان) در فرادرس

کلیک کنید

توزیع یکنواخت، نرمال، t-student، نمایی، کای ۲ و فیشر از نمونه توزیع‌های متغیر تصادفی پیوسته هستند.

مثال 3

فرض کنید نقطه‌ای به تصادف از محور اعداد حقیقی در بازه 0 تا 100 انتخاب می‌کنیم. اگر X را یک متغیر تصادفی به صورت فاصله این نقطه از مرکز نشان دهیم، واضح است که تکیه‌گاه این متغیر تصادفی به صورت $$(0,100)$$=S نوشته می‌شود.

حال فرض کنید که باید نقطه‌ای به تصادف بین ۱۰۰- تا ۱۰۰ از محور اعداد حقیقی انتخاب شود که بزرگتر از ۲۰ یا کوچکتر از ۵۰- باشد، اگر X را متغیر تصادفی در نظر بگیریم که فاصله این نقطه (مثلا a) را از مرکز مختصات نشان دهد آنگاه $$X=a-0$$ و تکیه‌گاه آن به صورت $$[--100,-50]\ \cup [20,+100]$$ =S خواهد بود.

تابع توزیع احتمال متغیر تصادفی پیوسته (Probability Distribution Function)

با توجه به پیوستگی‌ها متغیر تصادفی، یک خاصیت به خصوصیات تابع توزیع احتمال متغیر تصادفی پیوسته اضافه می‌شود که پیوستگی از چپ است. به این ترتیب می‌توان نوشت:

$$F_X(y)=F_X(y^+)=F_X(y^-)$$

به این شکل اگر بخواهیم $$P(X=y)$$ را محاسبه کنیم، خواهیم داشت:

$$P(X=y)=F_X(y)-F_X(y^-)=F_X(y^+)-F_X(y)=0$$

که نشان می‌دهد مقدار احتمال برای نقاط در تکیه‌گاه برابر با صفر است. در نتیجه برای نشان دادن جرم احتمال در هر نقطه از تکیه‌گاه، باید از مفهوم مشتق تابع توزیع احتمال کمک گرفت.

تابع چگالی متغیر تصادفی پیوسته (Density Function)

اگر X یک متغیر تصادفی با تابع توزیع احتمال پیوسته (مطلقا پیوسته) $$F_X$$ باشد،‌ آنگاه تابعی مثل $$f_x$$ وجود دارد که:

$$F_X(y)=\int_{-\infty}^y f_X(t)dt$$

در این حالت $$f_X$$ را تابع چگالی احتمال متغیر تصادفی X نامیده و می‌توان نوشت:

$$f_X(y)=F\prime _X(y)$$

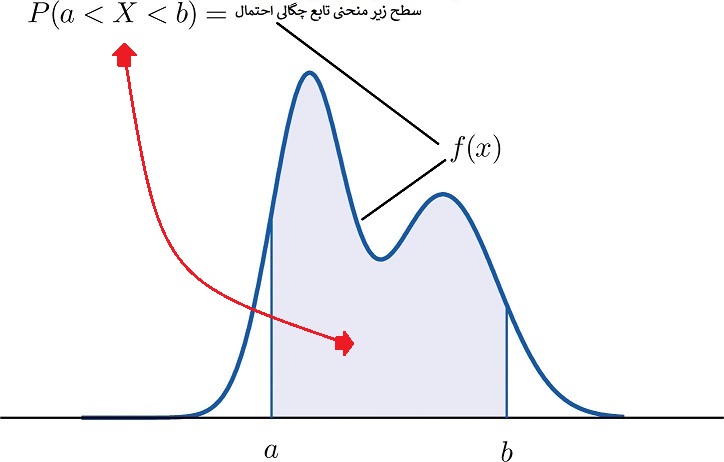
در نتیجه برای محاسبه احتمال برحسب تابع چگالی متغیر تصادفی X می‌توان رابطه زیر را محاسبه کرد:

$$P(a\leq X \leq b)=F_X(b)-F_X(a)=\int_{a}^b f_X(t)dt$$

به این ترتیب با توجه به مفهوم انتگرال مشخص است که این احتمال برابر با سطح زیر منحنی تابع چگالی در بازه (a,b)‌ است.

برای آشنایی با شیوه محاسبه مشتق می‌توانید به مطلب مفاهیم مشتق — به زبان ساده و برای انتگرال به مطلب انتگرال و روش های محاسبه — به زبان ساده مراجعه کنید.

مثال 4

با توجه به توضیحات مثال ۳ اگر جرم احتمال را به طور یکنواخت روی محور اعداد در نظر بگیریم، می‌توان تابع توزیع احتمال و تابع جرم احتمال را برای متغیر تصادفی X به صورت زیر نوشت:

$$F_X(y)=P(X\leq y)=\begin{cases} 0,\;\;\;y<0\\ \dfrac{y-0}{(100-0)},\;\;0\leq y<-100\\ 1,\;\;y>100\\ \end{cases}$$

ولی معمولا تابع توزیع احتمال متغیر تصادفی پیوسته را فقط برای تکیه‌گاه آن می‌نویسند. پس می‌توان فرم تابع توزیع احتمال چنین متغیر تصادفی را به صورت زیر نمایش داد:

$$F_X(y)=\dfrac{y}{100}, \;\;\;\; 0$$

با استفاده از رابطه‌ای که بین تابع چگالی احتمال و تابع توزیع احتمال متغیر تصادفی وجود دارد، می‌توان نوشت:

$$f_X(y)=\dfrac{dF_x(y)}{dy}=\dfrac{1}{100}, \;\;\; 0$$

همانطور که مشخص است برای متغیر تصادفی پیوسته می‌توان علامت > را با علامت $$\leq$$  و علامت < را با $$\geq$$ در تکیه‌گاه جایگزین کرد.