فرآیند گاوسی برای نمونه کوچک — پیاده‌ سازی در پایتون

امروزه بحث «مِه‌داده» یا «کلان داده» (Big Data) و تجزیه و تحلیل آن‌ها در همه حوزه‌ها، شنیده می‌شود. ولی گاهی لازم است که با داده‌های محدود و حتی معدود (Little Data) دست به تجزیه و تحلیل آماری بزنیم. در این نوشتار به بررسی مدل‌های ناپارامتری در مقابل روش‌های پارامتری خواهیم پرداخت و «فرآیند گاوسی پیش‌گو» (Gaussian Process Regressor) را برای استنباط آماری و تجزیه و تحلیل به کار می‌بریم. این مقاله برای کسانی که به عنوان تحلیل‌گر داده‌ها مشغول به کار هستند مفید خواهد بود. همچنین به منظور انجام محاسبات و رسم نمودارها از زبان برنامه‌نویسی پایتون استفاده کرده‌ایم که امروزه به عنوان ابزار سودمند برنامه‌نویسی در همه جا کاربرد دارد.

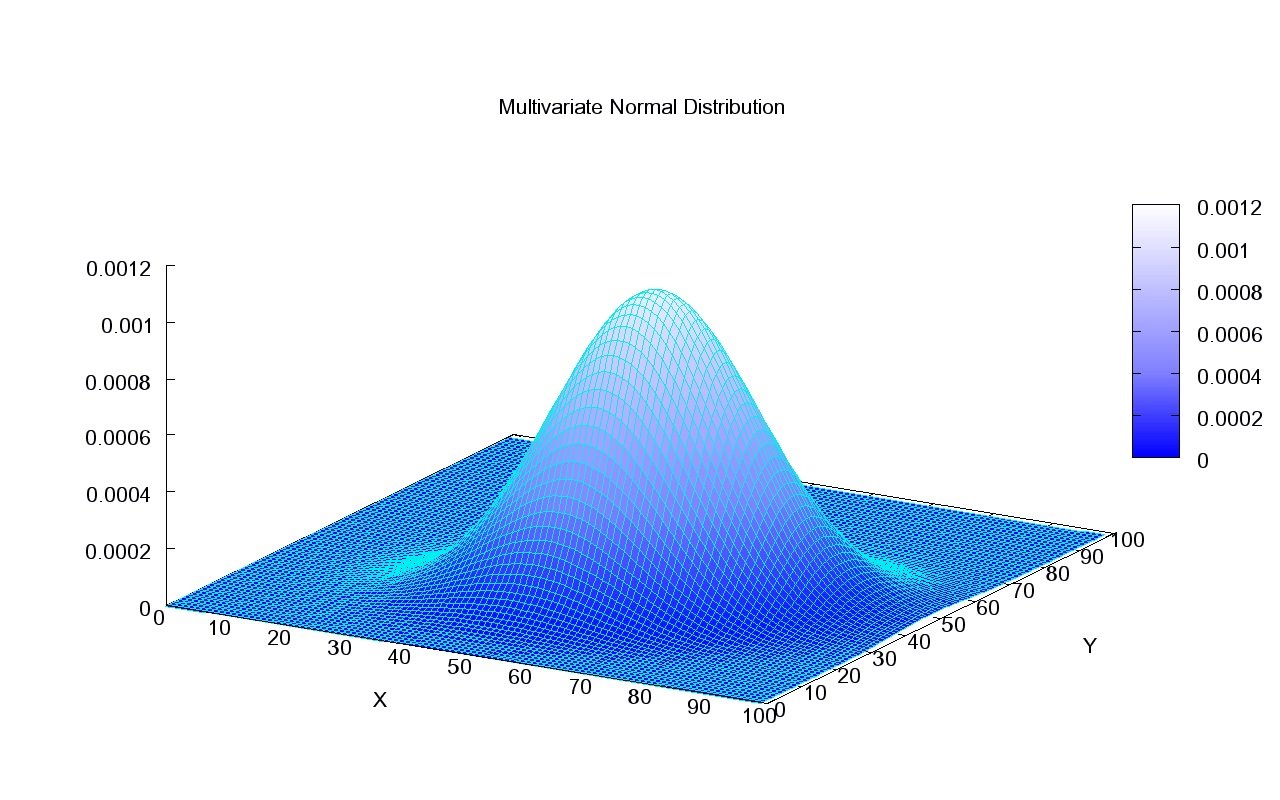
برای آشنایی با توزیع گاوسی (نرمال) بهتر است مطلب توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها را مطالعه کنید. همچنین به منظور آگاهی بیشتر در مورد رگرسیون و شیوه‌های اجرای آن به مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده و برای درک بهتر احتمال پسین و پیشین که در این مقاله به آن‌ها اشاره خواهیم کرد، به احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده مراجعه کنید. در ضمن خواندن نوشتار رسم نمودار داده ها در پایتون --- راهنمای تخصصی نیز خالی از لطف نیست.

فرآیند گاوسی برای داده‌های چند بُعدی

فرآیند گاوسی (Gaussian Process) در تئوری احتمالات، یک فرآیند تصادفی است که به صورت دنباله‌ای از متغیرهای تصادفی شناخته می‌شود. در این فرآیند، متغیرهای تصادفی معمولا برحسب مثلا زمان مرتب شده‌اند و هر زیر مجموعه متناهی از این متغیرها دارای توزیع گاوسی (نرمال) چند متغیره هستند.

فیلم آموزش فرایندهای تصادفی یا اتفاقی Stochastic Processes در فرادرس

کلیک کنید

بنابراین اگر $$\{X_t; t \in T\}$$ یک دنباله تصادفی باشد آنگاه $$X_{t_1,\ldots,t_k}=(X_{t_1},\ldots,X_{t_k})$$ دارای توزیع نرمال (گاوسی) چند متغیره هستند. به بیان دیگر در یک فرآیند گاوسی، هر ترکیبی خطی از مجموعه متناهی از فرآیند دارای توزیع نرمال یک متغیره است. مشخص است که $$T$$، مجموعه‌ای نامتناهی از اندیس‌های زمان یا مکان است. این فرآیند به علت فعالیت و تلاش‌های دانشمند آلمانی «کارل گاوس» (Carl Fridrich Gauss) در این زمینه، به نام او ثبت شده است. برای توصیف بهتر مدل و فرآیند گاوسی به یک مثال خواهیم پرداخت.

فرض کنید به عنوان مربی یک تیم بسکتبال (Basketball Coach) استخدام شده‌اید. البته از طرفی متخصص تحلیل داده‌ها (Data Scientist) نیز هستید. شعار مربی‌های بسکتبال در سه دستور کلی خلاصه می‌شود: کمتر توپ از دست بدهید، بیشتر به حلقه حمله کنید و همکاری تیم در کسب امتیاز را فراموش نکنید.

این گفته را می‌توان براساس تحلیل آماری و بهینه‌سازی به صورت زیر نیز نوشت:

• بُعد اول: باید تعداد پرتاب‌های آزاد بیشینه (Maximize) شود.
• بُعد دوم: تعداد اشتباهات منجر به از دست دادن توپ کمینه (Minimize) شود.
• خروجی یا تابع هدف: امتیاز در هر بازی بیشینه شود.

مشخص است که بُعد اول و دوم، شامل محدودیت‌هایی است که بواسطه آن‌ها خروجی یا تابع هدف حاصل می‌شود. حال به بررسی و مدل‌سازی امتیازات یک بازیکن خاص (مثلا با نام «استفان کوری» - Steph Curry) برحسب تعداد «اقدام به پرتاب‌های آزاد» (Free Throws Attempt) و «میزان از دست دادن توپ» (Turnovers) در هر بازی می‌پردازیم. به این ترتیب به نظر می‌رسد که با یک فرآیند گاوسی دو بُعدی مواجه هستیم و امتیازات نیز به عنوان متغیر وابسته این فرآیند در نظر گرفته شده است.

می‌توان فرآیند دو بعدی را بر حسب متغیرهای آن توصیف کرد. در بعد اول تعداد پرتاب‌ها و در بعد دوم نیز از دست دادن توپ قرار دارد. این متغیرها به عنوان متغیرهای «توصیف‌گر» (Regressor) در مدل ایجاد شده، نقش خواهند داشت. البته متغیر خروجی نیز که همان امتیاز کسب شده در هر بازی است به عنوان متغیر وابسته در ساختار مدل به کار خواهد رفت. ابتدا اطلاعات حاصل از این متغیرها را به صورت استاندارد در می‌آوریم بطوری که با محاسبه zscoreها، داده‌ها دارای میانگین صفر و واریانس ۱ خواهند شد. به همین علت روی محور افقی و عمودی در نمودارهای زیر، مقیاس‌ها در بین ۳- تا ۳+ تغییر می‌کند (به علت تغییرات کم روی محور عمودی فقط ناحیه بین ۲- تا ۲+ نمایش داده شده است.) این ویژگی را در مقدارهای متغیر هدف یا وابسته نیز می‌توان مشاهده کرد.

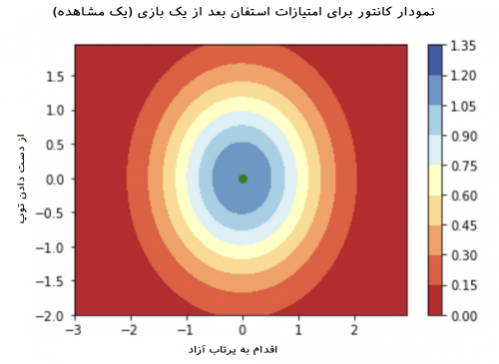
به این ترتیب، تصاویر زیر، توصیفی برای ارتباط بین متغیرهای مستقل و وابسته را براساس «نمودار کانتور» (Contour plot) نمایش می‌دهند. برای مثال مقدار ۱ در این نمودارها نشانگر اختلاف به میزان یک انحراف معیار از میانگین مسابقات NBA است. نقطه سبز درون نمودارها نیز بیانگر مقدار واقعی مشاهده شده است. به این ترتیب ناحیه آبی رنگ، نشانگر پیش‌بینی بهتر برای امتیاز توسط متغیرهای پیش‌گو است. هرچه به ناحیه قرمز رنگ برویم، پیش‌گویی با انحراف بیشتری همراه است. از طرفی راهنمای نمودار که طیف رنگ از قرمز تا آبی پر رنگ را نشان می‌دهد، کسب امتیاز او در بازی را به براساس مقدارهای استاندارد شده، نشان می‌دهد. به منظور تحلیل امتیازات و عملکرد این بازیکن، ابتدا براساس یک بازی، سپس به کمک دو بازی آخر او و سپس براساس سه و چهار بازی اخیر، دست به استنباط و تحلیل می‌زنیم. انتظار داریم هر چه تعداد بازی‌ها بیشتر می‌شود، اطلاعات و داده‌ها نسبت به عملکرد این بازیکن بیشتر و موثر‌تر شوند.

تحلیل بازی اول: همانطور که دیده می شود این بازیکن در اولین بازی خود به میانگین تعداد پرتاب‌ها و از دست دادن توپ بسیار نزدیک است. از طرفی امتیاز کسب شده توسط او کمی بیشتر از استاندارد است. مشخص است که همه برآوردها براساس فقط یک نقطه است در نتیجه به نظر می‌رسد انحرافی نیز وجود ندارد.

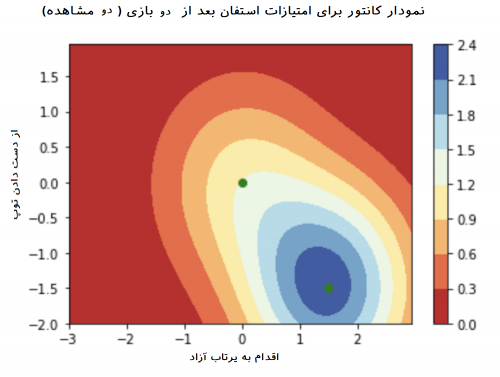
تحلیل بازی دوم: در این قسمت، تعداد پرتاب‌های آزاد او بیشتر شده و از طرفی هم خطاهای او در از دست دادن توپ کاهش یافته است و امتیازات بیشتری نیز کسب کرده است. تغییرات امتیازات نسبت به بازی اول نیز در نمودار به خوبی دیده می‌شود. نتایج بازی دوم در قسمت پایین-راست نمودار زیر دیده می‌شود. نقش نتایج بازی اول در تغییر شکل نمودار کانتور به خوبی دیده می‌شود. هر چند امتیازات در بازی دوم موثر است ولی مانند نمودار مربوط به بازی اول، پیش‌بینی‌ها کاملا دقیق نیستند.

تحلیل بازی سوم: در این نمودار، تعداد پرتاب‌های آزاد بازیکن بستکتبال، کمتر شده و از طرفی هم خطاهای او در از دست دادن توپ نیز افزایش داشته است. بنابراین دیده می‌شود که امتیازات کسب شده در این مسابقه کاهش داشته است زیرا ناحیه مربوط به این مسابقات با رنگ نارنجی نشان داده شده است. در نتیجه به نظر می‌رسد که او نسبت به مسابقه‌های قبلی، افت کرده است. به نظر می‌رسد که مدل‌بندی در این حالت برای پیش‌بینی امتیازات در بازی دوم مناسب است ولی خطای پیش‌بینی برای امتیاز بازی سوم زیاد است.

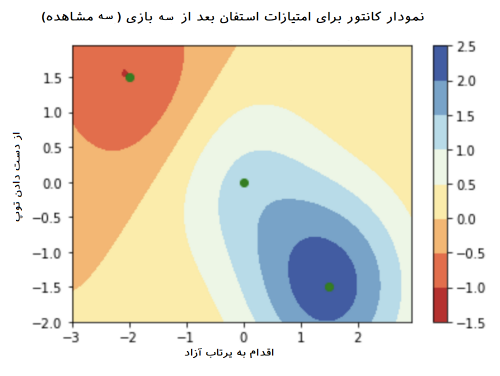
تحلیل بازی چهارم: نمودار آخر مربوط به چهار مسابقه آخر است. با توجه به افزایش تعداد پرتاب‌های آزاد بازیکن، امتیاز کسب شده در مسابقه چهارم افزایش نداشته است زیرا تعداد خطاهای از دست دادن توپ نیز افزایش نشان می‌دهد. به این ترتیب پیش‌گویی برای امتیاز حاصل از بازی چهار نیز با خطای زیادی همراه است. همچنین بازی دوم و به شکلی هم بازی اول به خوبی برآورد شده است.

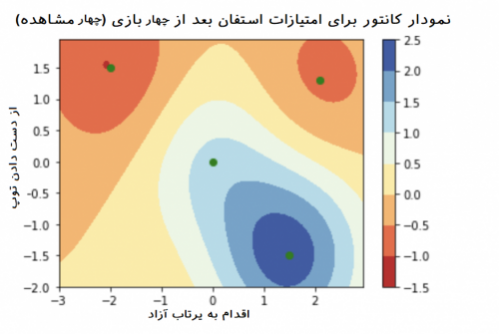
اگر برای بازی‌های بعدی نیز نمودارهای کانتور را رسم کنیم خواهیم دید که بین متغیرهای وابسته و مستقل یا توصیفی رابطه‌ای وجود دارد. برای مثال زمانی که بازیکن تعداد خطاهای زیادی دارد حتی اگر پرتاب‌های آزاد خوبی هم داشته باشد، امتیاز کسب شده برای او از میانگین NBA کمتر خواهد بود. ولی با توجه به نمودارهای ترسیم شده به نظر می‌رسد که بازیکن ما نسبت به میانگین (مقدار صفر برای امتیازات) از کارایی بیشتری برخوردار است زیرا میانگین امتیازات او از در این چهار مسابقه بیشتر از صفر است.

همانطور که دیده شد، با فرض نرمال (گوسی) بودن داده‌ها، امتیازات براساس نمودار کانتور در دو بُعد ترسیم شد. برای راحتی کار، کدهای رسم چنین نمودارهایی در ادامه قابل مشاهده است.

1X = np.array([[0, 0]])
2y = np.array([[1.2]])
3gp = GaussianProcess(X, y)
4gp.update([[1.5, -1.5]], [[2.3]]) # second data point
5gp.update([[-2,1.5]], [[-1.0]]) # third data point
6gp.update([[2.1,1.3]], [[-0.6]]) # fourth data point
7
8delta = 0.05 # changes granularity of the contour map
9x = np.arange(-3.0, 3.0, delta)
10y = np.arange(-2.0, 2.0, delta)
11X, Y = np.meshgrid(x, y)
12Z = []
13for i in x:
14    for j in y:
15        # I take only the 0th (first) element since that is the prediction
16        # The second element is the uncertainty
17        Z.append(gp.new_predict([[i,j]])[0])
18
19results = np.array([Z]).reshape(len(x), len(y))
20plt.figure()
21CS = plt.contourf(X, Y, results.T,  cmap='RdYlBu')
22plt.colorbar()
23for data in gp.X:
24    plt.scatter(data[0], data[1], c="g")
25plt.title("Contour Map of Steph Curry's Scoring \n After 4 Data Points (Games)")
26plt.xlabel("Free Throws")
27plt.ylabel("Turnovers")

مدل‌سازی فرآیند گاوسی

سوالی که در رابطه با این مثال مطرح می‌شود، این است که چگونه براساس داده‌های مربوط به این چهار بازی، استنباط یا مدل‌سازی آماری انجام دهیم. در ادامه به شیوهای مدل‌سازی با روش‌های پارامتری مانند تکنیک کمترین مربعات عادی و ناپارامتری مانند فرآین دگاوسی اشاره خواهیم داشت.

فیلم آموزش ساختمان داده ها با پایتون در فرادرس

کلیک کنید

مدل‌ها و روش‌های پارامتری

یکی از روش‌های مدل‌سازی مرسوم در آمار، استفاده از تکنیک OLS یا کمترین مربعات عادی (Ordinary Least Squares) است. سادگی در انجام محاسبات و تفسیر پذیری این مدل، آن را به عنوان ابزار اصلی تحلیل‌گرهای داده (Data Scientist) در آورده است. ولی زمانی که تعداد نقاط و مقادیر مشاهده شده از متغیرها، کم باشد، استفاده از این روش، با محدودیت‌هایی مواجه می‌شود. انتخاب توزیع نرمال برای خطای مدل از ویژگی‌های اصلی روش OLS محسوب می‌شود. بنابراین اگر حجم داده‌ها کم باشد، نمی‌توانیم از قضیه حد مرکزی یا قانون ضعیف اعداد بزرگ استفاده کنیم و توزیع خطا را نرمال فرض کنیم.

برای مثال فرض کنید که می‌خواهیم ارتباط بین میزان هزینه تبلیغات (Spent $) و سهم بازدید‌های مطالب در یک شبکه‌های اجتماعی (Social Media Shares) را مورد بررسی قرار دهیم. اگر نمودار مربوط به این دو متغیر یه مانند تصویر زیر باشند به خوبی می‌توان برای پیش‌بینی سهم در شبکه‌های اجتماعی، بودجه و هزینه را مشخص کرد. به خوبی دیده می‌شود که با افزایش هزینه تبلیغات، سهم بازدید سایت در میان شبکه‌های اجتماعی نیز افزایش می‌یابد.

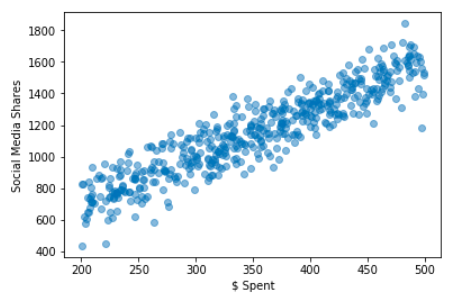
البته توجه دارید که این نمودار براساس تعداد نقاط زیادی ترسیم شده است. بنابراین پیش‌بینی توسط این نمودار با دقت و صحت مناسب صورت خواهد گرفت. چنین نموداری را در پایتون می‌توان به راحتی ترسیم کرد. کد زیر به این منظور تهیه شده است.

1import numpy as np
2θ = 3
3bias = 100
4X = np.array([np.random.uniform(200,500) for i in range(500)])
5ε = np.array([np.random.normal(0,1) for i in range(500)])
6y = X * θ + bias + ε

به این ترتیب دیده می‌شود که با شبیه‌سازی 500 نقطه از توزیع یکنواخت در فاصله ۲۰۰ تا ۵۰۰ به عنوان هزینه (برحسب دلار) به عنوان متغیر تصادفی $$X$$ به همراه خطای نرمال (متغیر تصادفی $$\epsilon$$) با میانگین صفر و واریانس ۱، مدل مطابق با رابطه زیر شبیه‌سازی شده است.

$$\large Y=X\times \theta +bias+\epsilon$$

البته این مدل را اغلب به شکل دیگری نیز نشان می‌دهند. در حالتی که رگرسیون ساده یک متغیره برای مدل‌سازی مورد نظر باشد، براساس پارامترهای $$\beta$$، می‌توان ساختار رابطه بین متغیر وابسته و مستقل را به صورت زیر نوشت.

$$\large y = \beta_0+\beta_1 \times x+\epsilon$$

واضح است که در این مدل $$beta_0$$‌ همان Bias در کد پایتون است. همچنین $$\beta_1$$ نیز همان پارامتر $$\theta$$ در برنامه نوشته شده محسوب می‌شود. البته برای به کارگیری چنین مدل‌های در تکنیک OLS شرایطی وجود دارد که بخصوص برای حجم داده‌های کوچک محقق شدن این شرایط بسیار بعید است. زمانی که مدل به صورت دو جمله‌ای مرتبه ۲ نوشته شود، مدل رگرسیونی به صورت زیر نوشته می‌شود.

$$\large y = \beta_0+\beta_1 \times x+\beta_2 \times x^2 +\epsilon$$

ولی اگر مدل برای داده‌ها، به صورت غیرخطی (مثلا تابع سینوسی) باشد. نمی‌توان از روش OLS استفاده کرد. به عنوان مثال فرض کنید قیمت کالاها در دوره تعطیلات زمستانی (کریسمس) ممکن است از مدل سینوسی پیروی کند. نمودار زیر این حالت را نشان می‌دهد. در ادامه سعی داریم برای چنین حالتی از فرآیند گاوسی استفاده کرده و مدل مناسب را ارائه دهیم.

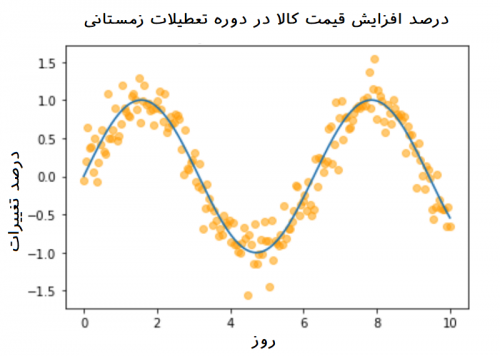
مدل‌ها و روش‌های ناپارامتری

همانطور که در قسمت قبل اشاره شد، استفاده از تکنیک OLS نیازمند شرایطی که است در همه مواقع قابل بررسی و محقق شدن نیست. به همین دلیل روش‌های ناپارامتری ارزشمند و کارا هستند. البته باید توجه داشت که در صورت وجود توزیع نرمال برای خطا، روش‌های پارامتری و OLS بسیار بهتر و با خطای بسیار کمتری نسبت به روش‌های ناپارامتری عمل می‌کنند. ویژگی‌های روش‌ها و مدل‌های ناپارامتری در زیر فهرست شده‌اند.

• مدل‌های ناپارامتری هیچ فرضی برای توزیع احتمالی جامعه آماری ندارند. برای مثال در تکنیک «نزدیک‌ترین همسایه» - KNN یا (K-Nearest Neighbor) احتیاجی نیست که توزیع جامعه‌ آماری مشخص باشد در حالیکه در شیوه «خوشه‌بندی k-میانگین» (K-means Clustering) فرض بر این است که داده‌ها مستقل از یکدیگر و از یک جامعه آماری با توزیع نرمال با واریانس ثابت و یکسان آمده‌اند. همچنین در مدل بیز ساده (Naive Bayes) توزیع مزدوج برای مشاهدات، تزویع نرمال در نظر گرفته شده و شرط استقلال نقاط نیز باید وجود داشته باشد.
• پیچیدگی مدل‌های ناپارامتری با افزایش تعداد داده‌ها افزایش می‌یابد. اگر به جای ۱۰ مشاهده، ۱۰۰۰ مشاهده وجود داشته باشد، استفاده از مدل‌های ناپارامتری موردی نخواهد داشت و می‌توان از مدل‌های پارامتری استفاده کرد. برای مثال فرض کنید که برای «رگرسیون کرنل گاوسی» (Gaussian Kernel Regression)، میانگین مقدار پیش‌بینی شده برای متغیر وابسته $$y^*$$ برحسب متغیر مستقل $$x^*$$ به کمک مشاهدات $$x_i$$ مطابق با رابطه زیر نوشته شده باشد. واضح است که با افزایش نقاط، محاسبات بیشتری برای کرنل $$K$$ احتیاج است.

$$\large y^* =\dfrac{\sum_{i=0}^n K(x^*,x_i)y_i}{\sum_{i=0}^n K(x^*,x_i)},\;\; K(x^*,x_i)=\exp[\dfrac{-(x_i-x^*)^2}{2\sigma^2}]$$

حال سوالی که در اینجا مطرح می‌شود این است که چه زمانی تحلیل‌گر داده باید از روش‌های ناپارامتری استفاده کند؟ شرایط استفاده از تکنیک‌های آماری ناپارامتی در زیر فهرست شده است.

• نامعلوم یا نامشخص بودن فضای مقداری برای ویژگی‌ها یا متغیرها.
• محقق نشدن بعضی از شرایط حساس در روش‌های پارامتری مانند یکسان بودن واریانس، استقلال و همچنین توزیع نرمال برای باقی‌مانده در مدل رگرسیون OLS.
• وجود داده‌‌های پرت در مشاهدات بطوری که روش‌های ارزیابی مانند «میانگین مربعات خطا» (Mean Square Error - MSE) دچار مشکل در تفسیر نتایج شوند. به این ترتیب تکنیک‌هایی که از این معیارها استفاده می‌کنند، مانند گرادیان کاهشی، ناکارآمد خواهند بود.

پیاده‌سازی فرآیند گاوسی

اگر از توزیع داده‌ها اطلاع ندارید و می‌خواهید به مدل‌سازی بپردازید، شاید یک روش ساده و مستقیم، استفاده از فرآیند گاوسی باشد. در اینجا فرض شده است که هیچ اطلاعاتی در مورد تغییرات و توزیع داده‌ها نسبت به زمان و پارامترهای توزیع‌شان نداریم. در چنین حالتی برای شروع، استفاده از «فرآیند گاوسی» (GP) به عنوان یک راه حل اولیه مناسب به نظر می‌رسد.

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

همانطور که در قسمت‌های قبلی اشاره شد، فرایند گاوسی دنباله‌ای از متغیرهای تصادفی است که هر زیر مجموعه‌ای از آن‌ها دارای توزیع گاوسی باشند که توسط میانگین و ماتریس واریانس-کوواریانس قابل تشخیص‌اند. در دیگر نوشتارهای فرادرس با شیوه ترسیم نمودارهای ریاضی آشنا شده‌اید و می‌دانید که برای نمایش توابع ریاضی با مقادیر حقیقی، باید از بی‌نهایت نقطه استفاده شود. در تصویرهای زیر نمودار تابع $$Sin(X)$$ به کمک ۱۰ و ۱۰۰۰۰۰۰۰ نقطه ترسیم شده است.

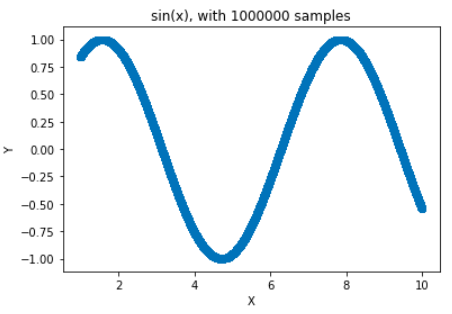
کدی که در ادامه می‌بینید برای کشیدن این نمودارها در پایتون نوشته شده. مشخص است که ۱ میلیون نقطه در فاصله بین ۱ تا ۱۰ تولید شده و محاسبه تابع سینوس برای این نقطه‌ها صورت گرفته است. در انتهای کد نیز به کمک مختصات دکارتی، نمودار تابع سینوس (Sine) ترسیم شده است.

1X = np.linspace(1,10,1000000)
2y = np.sin(X)
3plt.scatter(X, y)
4plt.xlabel("X")
5plt.ylabel("Y")
6plt.title("sin(x), with 1000000 samples")

اساس فرآیند گاوسی در «توزیع حاشیه‌ای» (Marginal Distribution)  و «توزیع شرطی» (Conditional Distribution) نهفته است که به کمک داده‌های مشاهده نشده از بی‌نهایت متغیر تصادفی (دنباله تصادفی یا فرآیند تصادفی) حاصل می‌شود. به این ترتیب به کمک مشاهداتی که از زیرمجموعه فرآیند گاوسی حاصل شده است برای پیش‌بینی و محاسبه توزیع احتمال استفاده می‌شود. خوشبختانه توزیع حاشیه‌ای و شرطی زیرمجموعه از متغیرهای تصادفی گاوسی، باز هم دارای توزیع نرمال هستند. به این ترتیب روابط زیر را می‌توان در نظر گرفت.

$$\large p(X|Y)=N(\mu_x+\Sigma_{x,y}\Sigma^{-1}_{y,y}(y-\mu_y), \Sigma_{x,x}-\Sigma_{x,y}\Sigma^{-1}_{y,y}\Sigma_{y,x})$$

رابطه ۱

برطبق قوانین شرطی و توزیع حاشیه‌‌ای به کمک قضیه بیز نیز می‌توان رابطه زیر را استنباط کرد.

$$\large p(Y|X)=N(\mu_y+\Sigma_{y,x}\Sigma^{-1}_{x,x}(x-\mu_x), \Sigma_{y,y}-\Sigma_{y,x}\Sigma^{-1}_{x,x}\Sigma_{x,y})$$

رابطه ۲

در رابطه اول، ماتریس‌های کوواریانس زیادی وجود دارد. برای مثال $$\Sigma_{x,x}$$‌ واریانس متغیر‌های $$X$$ را نشان می‌دهد. همچنین $$\Sigma_{x,y}$$ نیز بیانگر ماتریس کوواریانس بین $$X$$ و $$Y$$ است. اگر بین $$X$$ و $$Y$$ رابطه خطی برقرار باشد می‌توان فرمول زیر را بین متغیر مستقل $$X$$ با متغیر وابسته $$Y$$ نوشت.

$$\large p(X)=N(\mu,\Sigma)$$

$$\large p(Y)=N(AX+b,\Sigma,\mathbf{N})$$

از طرفی توزیع توام متغیرهای تصادفی $$X$$ و $$Y$$ به شکل زیر خواهد بود.

$$\large p(\begin{bmatrix}X \\ Y \end{bmatrix}) = N \left(\begin{bmatrix} \mu \\ AX+b\end{bmatrix},\begin{bmatrix} \Sigma & \Sigma A^T \\ A \Sigma & N+A\Sigma A^T \end{bmatrix}\right)$$

قدم بعدی تبدیل «توزیع توام» (Joint Distribution) به فرآیند گاوسی (GP) است. طبق فرآیند گاوسی باید توزیع توام زیرمجموعه‌ای از این دنباله متغیرهای تصادفی از توزیع گاوسی با میانگین و ماتریس واریانس مشخصی آمده باشد. برای راحتی کار (یا براساس باورهای پیشین) میانگین داده‌ها را صفر در نظر می‌گیریم. توجه داشته باشید که ما براساس مشاهداتی که از قبل در مورد متغیر تصادفی $$X$$ داریم سعی در پیش‌بینی متغیر تصادفی $$Y$$‌ داریم. بنابراین نیازمند ایجاد رابطه یا تابعی مثل $$f^*$$‌ هستیم که بتواند این پیش‌بینی را به صورت یک رابطه ریاضی نشان دهد. این تابع باید به مانند متغیر تصادفی $$Y$$ یک توزیع توام نرمال چند متغیره را ایجاد کند.

$$\large p(\begin{bmatrix}Y \\ f^* \end{bmatrix}) = N \left( 0 ,\begin{bmatrix} K(X,X)+\sigma^2_nI & K(X,X^*) \\ K(X^*,X) & K(X^*,X^*) \end{bmatrix}\right)$$

در این رابطه $$X$$ و $$Y$$ به ترتیب متغیرهای توصیفی و خروجی (وابسته) برمبنای «داده‌های آموزشی» (Training Set) هستند. همچنین $$X^*$$ و $$f^*$$ نیز ویژگی‌ها یا متغیرهای ورود و خروجی هستند که باید پیش‌بینی شوند. همچنین $$\sigma^2$$ نیز واریانس خطاها را نشان می‌دهد. همچنین به توابع $$K$$ که به عنوان کرنل معرفی شده‌اند نیز توجه داشته باشید.

فرض کنید که $$n$$ تعداد داده‌های آموزشی و $$n^*$$‌ نیز «داده‌های آزمایشی» (Test Set) باشند. در این صورت $$K(X,X^*)$$ یک ماتریس $$n\times n$$ است که کوواریانس بین نقاط آموزشی و آزمایش را بیان می‌کند. به همین ترتیب ماتریس $$K(X^*,X^*)$$ نیز واریانس مقادیر آزمایشی را در قالب یک ماتریس $$n^* \times n^*$$ نمایش می‌دهد. به منظور ساده‌تر کردن محاسبات در اینجا از «کرنل پایه شعاعی» (Radial Basis Function Kernel) استفاده می‌کنیم. این کرنل به صورت زیر نوشته می‌شود.

$$\large K(X,X')=\exp \Big(- \dfrac{||X-X'||^2}{2\sigma^2}\Big)$$

البته توجه داشته باشید که در اینجا منظور از $$||X-X'||^2$$ مربع فاصله اقلیدسی بین دو بردار $$X$$ و $$X'$$ است. کدی که در ادامه مشاهده می‌کنید این کرنل را به وسیله کتابخانه NumPy در پایتون، پیاده‌سازی کرده‌ و برای بردار $$(0,1,2,2)$$ بدست آورده‌ است. این محاسبات به صورت یک کلاس در آمده تا قادر به فراخوانی آن در برنامه‌های مربوط به قسمت‌های دیگر نیز باشیم.

1class RadialBasisKernel:
2    @staticmethod
3    def compute(x_1, x_2):
4        return np.exp(-0.5 * np.subtract.outer(x_1, x_2) ** 2)
5
6# toy example
7x = np.array([0,1,2,2])
8RadialBasisKernel.compute(x, x)

نکته: از آنجایی که احتیاج به یک ماتریس $$n \times n$$‌ داریم به جای استفاده از تابع np.subtract از np.subtract.outer‌ استفاده کرده‌ایم.

نتیجه اجرای این کرنل روی داده‌های برداری $$[0,1,2,2]$$ به صورت زیر است.

1array([[ 1.        ,  0.60653066,  0.13533528,  0.13533528],
2       [ 0.60653066,  1.        ,  0.60653066,  0.60653066],
3       [ 0.13533528,  0.60653066,  1.        ,  1.        ],
4       [ 0.13533528,  0.60653066,  1.        ,  1.        ]])

از این به بعد از توزیع نرمال استاندارد (با میانگین صفر و واریانس ۱) به عنوان توزیع پیشین استفاده خواهیم کرد. فرض کنید قرار است یک مقدار تصادفی از متغیر $$X$$ انتخاب شده، مقدار متغیر وابسته ($$Y$$) برای آن تعیین شود. در محاسبه زیر $$x=2.3$$ تعیین شده است.

1x = 2.3
2X = np.array([x]) # initial training feature space value
3y = .922
4Y = np.array([y]) # initial training output value

نکته: توجه داشته باشید که در اینجا $$x$$ مقدار مشاهده شده برای یک نقطه انتخابی است ولی $$X$$ و $$y$$ مربوط به کل داده‌های آموزشی ورودی و خروجی هستند.

تابعی که برای پیش‌بینی متغیر وابسته به کار می‌رود، براساس رابطه‌های قبلی، به صورت زیر نوشته می‌شود. البته توجه داشته باشید که در این میان، امید ریاضی و ماتریس کوواریانس نیز برآورد شده است.

$$\large f^*|X,y,X^* \sim N(\overline{f^*},cov(f^*))$$

$$\large \overline{f^* }= \operatorname{E}(f^*|X,y,X^*)=K(X^*,X)[K(X,X)+\sigma^2_nI)^{-1}y$$

رابطه ۳

$$\large cov(f^*)=K(X^*,X^*)-K(X^*,X)[K(X,X)+\sigma^2_nI]^{-1}K(X,X^*)$$

رابطه ۴

به منظور پیاده‌سازی این محاسبات از کد پایتون زیر استفاده کرده‌ایم تا مقدار پیش‌بینی شده برای x_new را محاسبه کنیم. واضح است که این مقدار همان میانگین یا امید ریاضی تعریف شده در رابطه بالا است که با $$\overline{f^*}$$ نمایش داده شد. به این ترتیب براساس داده‌های مشاهده شده (آموزشی) برای مقدار x_new، متغیر وابسته در y_pred محاسبه می‌شود.

1def new_predict(x_new, X, y):
2    """
3    x_new: the new datapoint you'd like to predict on
4    X: the existing training data
5    y: the existing training outputs
6    return: a mean prediction, and a covariance (sigma) prediction
7    """
8    k_x_new_x = [Kernel.get(x_new, x_i) for x_i in X]
9    k_x_x = Kernel.get(X,X) # covariance matrix for existing training points
10    k_x_new_x_new = Kernel.get(x_new, x_new) # covariance matrix for new test points
11    y_pred = np.dot(k_x_new_x, np.linalg.inv(k_x_x)).dot(y) # Equation 2.23
12    updated_sigma = k_x_new_x_new - np.dot(
13        k_x_new_x, np.linalg.inv(k_x_x)).dot(k_x_new_x) # Equation 2.24
14    return y_pred.squeeze(), updated_sigma.squeeze()

نقطه تمرکز این محاسبات، پیدا کردن y_pred و updated_sigma است. همانطور که در شیوه‌ پیدا کردن مقدار y_pred مشخص است، ماتریس کرنل $$K(X,X)$$ دارای یک عبارت اضافه به صورت $$\sigma^2_nI$$ است. این جمله به این علت به کرنل اضافه شده است که گاهی ممکن است این ماتریس معکوس‌پذیر نباشد، اضافه کردن مقدار ثابت برحسب واریانس به عناصر قطر اصلی آن باعث می‌شود که ماتریس از حالت «تکین» (Singular) خارج شود. مشخص است که این عمل با ضرب واریانس ثابت (مقداری کمتر از 0.002) در ماتریس یکه ($$I$$) و جمع با ماتریس کرنل صورت گرفته است.

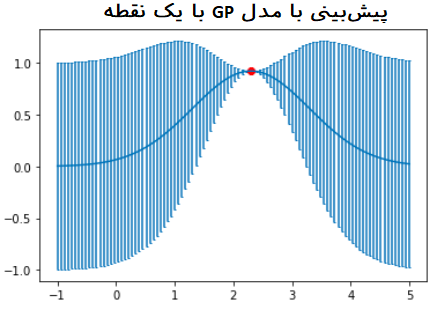
حال فرض کنید به کمک داده‌های آموزشی قبلی، می‌خواهیم برای ۱۰۰ مقدار مختلف پیشی‌بینی در فاصله ۱- تا ۵ پیدا کنیم در حالیکه فقط یک نقطه ($$x=2.3, y=0.922$$) به عنوان نقطه آموزشی داریم.

1x_pred = np.linspace(-1,5,100)
2predictions = [new_predict(i) for i in x_pred]
3# these next few lines are entirely from Chris Fonnesbeck's blog post at Domino Data Lab!
4y_pred, sigmas = np.transpose(predictions) 
5plt.errorbar(x_pred, y_pred, yerr=sigmas, capsize=1)
6plt.plot(X, y, "ro")
7plt.title("GP Predictions Given Single Training Point (2.3, 0.922)")

نموداری که در ادامه قابل مشاهده است، پیش‌بینی‌ها را با خطوط آبی نشان داده است که همان فرآیند گاوسی است. از طرفی برای هر مقدار پیش‌بینی شده، نمودار میله خطا (Error bar) نیز براساس انحراف استاندارد رسم شده است. این خطوط نشان می‌دهند که با دور شدن از نقطه آموزشی، میزان خطای برآورد برای نقاط آزمایشی بیشتر خواهد شد. مشخص است که میانگین توزیع گاوسی همان نقطه آموزشی است که در نمودار با رنگ قرمز نشان داده شده.

حال بهتر است که کدهای تولید شده را به صورت یک class در پایتون درآوریم. این کلاس را به نام GaussianProcess نام‌گذاری کرده‌ایم. همچنین با استفاده از یک روش ()update امکان به روزآوری محاسبات ماتریس کوواریانس برای مشاهدات جدید بوجود آمده است. درست بعد از محاسبه به‌روزآوری (update)، محاسبه ماتریس کوواریانس کرنل K و معکوس آن صورت گرفته است. در قسمت‌های بعدی از این کلاس استفاده کرده و محاسبات را پی‌می‌گیریم.

1from sklearn.metrics.pairwise import rbf_kernel
2
3class Kernel:
4    
5    condition = 1e-3 # add extra condition to reduce singular value issue
6    
7    @staticmethod
8    def convert_to_float(num):
9        return_val = np.float(num) if np.isscalar(num) else num
10        return return_val
11    
12    @staticmethod
13    def get(x_1, x_2, condition=1e-3): 
14        K = rbf_kernel(x_1, x_2) # use sklearn's rbf_kernel()
15        if type(x_1) == list:
16            condition_matrix = condition * np.eye(K.shape[0]) if K.shape[0] == K.shape[1] else np.eye(K.shape[1])     
17        else:
18            condition_matrix = condition
19        return (K + condition_matrix)
20
21class GaussianProcess:
22    
23    def __init__(self, X, y, condition=1e-5):
24        self.X = X
25        self.y = y
26        # precompute the covariance matrix and invert it
27        self.k_x_x = Kernel.get(self.X,self.X, condition)
28        self.inv_k_x_x = np.linalg.inv(self.k_x_x)
29
30    def update(self, x, y, condition=1e-5):
31        
32        """
33        x: new datapoint to incorporate
34        y: corresponding output value(s) to incorporate
35        condition: the σ^2(Ι) portion of the kernel, by default set to a small amount
36        """
37        
38        self.X = np.concatenate((self.X,x), axis=0)
39        self.y = np.concatenate((self.y,y), axis=0)
40        
41        # update the covariance matrix for existing training points
42        self.k_x_x = Kernel.get(self.X,self.X, condition)
43        self.inv_k_x_x = np.linalg.inv(self.k_x_x)
44    
45    def new_predict(self, x_new, noise=0):
46        k_x_new_x = np.array([Kernel.get(x_new, np.array([x_i])).reshape(-1) for x_i in self.X])
47        k_x_new_x_new = Kernel.get(x_new, x_new) # covariance matrix for new test points
48        y_pred = np.dot(k_x_new_x.T, self.inv_k_x_x).dot(self.y) # Equation 2.23
49        updated_sigma = k_x_new_x_new - np.dot(
50            k_x_new_x.T, self.inv_k_x_x).dot(k_x_new_x) # Equation 2.24
51        return y_pred.squeeze(), updated_sigma.squeeze() # using Fonnesbeck code here!
52    
53    def generate_predictions(self, prediction_interval, noise=0):
54        predictions = [self.new_predict(np.array([[i]]), noise) for i in prediction_interval]
55        # these next few lines are entirely from Chris Fonnesbeck's blog post at Domino Data Lab!
56        y_pred, sigmas = np.transpose(predictions) 
57        plt.errorbar(prediction_interval, y_pred, yerr=sigmas, capsize=1)
58        plt.plot(self.X, self.y, "ro")
59        plt.title(f"GP Predictions Given {len(self.y)} Training Points (In Red)")

همانطور که در کد مشاهده می‌کنید، به منظور محاسبه مربع فاصله اقلیدسی از حلقه تکرار استفاده نشده است. در عوض با استفاده از اتحادها می‌دانیم رابطه زیر برقرار است.

$$\large ||a-b||^2= ||a||^2+||b||^2-2a.b$$

به این ترتیب محاسبه مربع فاصله اقلیدسی در حالت چندگانه به سادگی صورت می‌گیرد. برای اینکه تفاوت سرعت در انجام محاسبات در حالت عادی و با استفاده از اتحاد ریاضی و شکل برداری را متوجه شوید، کد زیرا را اجرا کنید. در اینجا از کتابخانه scikit-learn برای انجام محاسبات برداری کمک گرفته‌ایم.

1import numpy as np
2import time
3from sklearn.metrics.pairwise import rbf_kernel
4x = np.random.rand(10000)
5x = x.reshape(100,100)
6distances = []
7γ = -.5
8start = time.time()
9for i in x:
10    for j in x:
11        distances.append(np.exp(γ * np.linalg.norm(i - j) ** 2))
12np.array(distances).reshape(len(x),len(x))
13end = time.time()
14time1 = end - start
15print(f"Runtime using for loops: {time1}")
16
17start2 = time.time()
18rbf_kernel(x, gamma= .5)
19end2 = time.time()
20time2 = end2 - start2
21print(f"Runtime using vectorized matrix operations: {time2}")
22# Runtime using for loops: 0.120
23# Runtime using vectorized matrix operations: 0.009

همانطور که در انتها به عنوان خروجی، مشاهده می‌کنید، زمان انجام محاسبات در حالت حلقه برداری و با استفاده از کتابخانه scikit-learn حدود ۱۰ برابر بیشتر از زمانی است که به صورت حلقه تکرار محاسبات صورت بگیرد. مشخص است که محاسبه ماتریس کوواریانس با ابعاد ۱۰۰ در ۱۰۰ با استفاه از حلقه تکرار حدود 0.120 ثانیه بطول انجامیده در حالیکه همین کار به کمک محاسبات برداری فقط 0.009 ثانیه زمان لازم دارد.

مدل‌سازی برای تابع سینوس به کمک فرایند گاوسی

دوباره به مثال مربوط به تابع سینوس باز می‌گردیم. در این قسمت سعی داریم به کمک توابع و کلاس‌هایی که تولید کردیم، پیش‌بینی برای تابع سینوس را به کمک یک فرآیند گاوسی ایجاد کنیم. فرض کنید که فقط ۱۰ مشاهده برای پیش‌بینی چنین تابعی در اختیار داریم. از میان این نقاط به طور تصادفی، نقطه‌هایی را برای عمل برآورد به کار خواهیم گرفت.

فیلم آموزش مقدماتی کار با پایگاه های داده در پایتون Python در فرادرس

کلیک کنید

این نقطه‌ها در نمودارهای ترسیم شده به رنگ قرمز هستند. در ضمن عمل برآورد و پیش‌بینی را طبق مدل گاوسی برای ۱۰۰ نقطه در فاصله ۱ تا ۱۰ به پیش می‌بریم. در نمودارهای ترسیم شده این نقطه‌ها با رنگ نارنجی نشان داده شده‌اند.

1NUM_TRAINING_SAMPLES = 10
2prediction_interval = np.linspace(1,10,100)
3start = int(np.random.uniform(1,100))
4gp = GaussianProcess([X_sin[start]], [y_sin[start]])
5indices = range(len(prediction_interval))
6for i in range(NUM_TRAINING_SAMPLES):
7    start = np.random.choice(indices, replace=False)
8    print(start)
9    gp.update(X_sin[start], y_sin[start])
10    
11gp.generate_predictions(prediction_interval, noise=1e-7)
12plt.scatter(X_sin, y_sin, c="orange", alpha=0.8)

واضح است که منحنی آبی رنگ نیز همان برآورد و پیش‌بینی برای تابع سینوس را نشان می‌دهد. میله‌های خطا نیز در نمودارها دیده می‌شود.

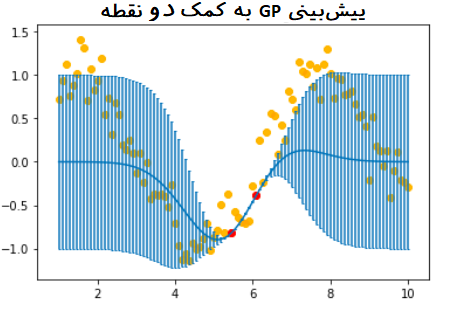
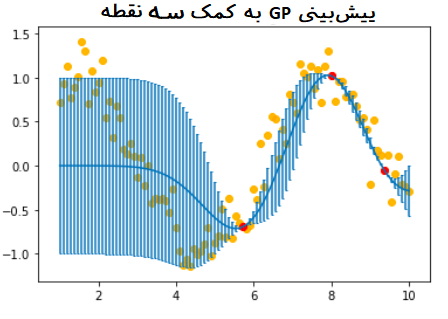
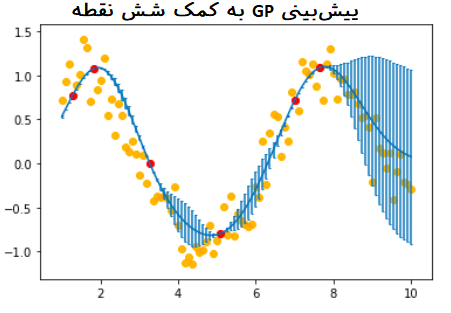
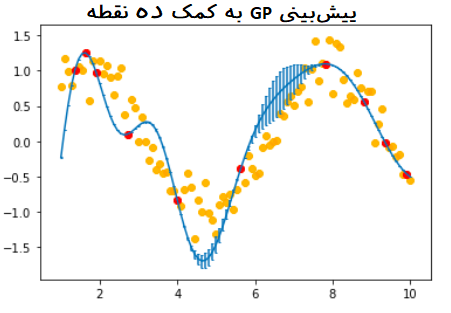
در آخرین نمودار، زمانی که از همه ۱۰ نقطه آموزشی استفاده شده است، مدل قادر است که پیش بینی مناسبی برای نقاط مربوط به تابع سینوس ارائه دهد. با توجه به کمبود نقاط آموزشی یا فاصله بیشتر بین آن‌ها در بازه ۵ تا ۸، میزان خطا در این ناحیه بیشتر از بقیه نواحی است.

محدودیت‌های استفاده از فرآیند گاوسی

هر چند استفاده از فرآیند گاوسی، در بسیاری از موارد امکان پیش‌بینی مناسب را می‌دهد ولی باید با محدودیت‌ها و معایب آن نیز آشنا باشیم.

بار محاسباتی در مدل‌های فرآیند گاوسی، زیاد است. از طرفی برای بدست آوردن ماتریس کوواریانس حجم زیادی از حافظه اشغال می‌شود. همانطور که در رابطه‌های ۳ و ۴ دیده شد، باید معکوس یک ماتریس $$n \times n$$ محاسبه شود که $$n$$ تعداد مشاهدات آموزشی هستند. از آنجایی که پیچیدگی انجام این محاسبه حتی طبق روش تفکیک چولسکی (Cholesky Decomposition) از مرتبه $$O(n^3)$$ است، مشخص می‌شود که زمان اجرای این محاسبات زیاد است. به همین ترتیب میزان حافظه اشغالی توسط این الگوریتم از مرتبه $$O(n^2)$$‌ است. البته روش‌هایی برای کاهش بعد ماتریس کرنل نیز وجود دارد که با استفاده از تجزیه آن سعی دارد که بعد آن را از $$n \times n$$ به $$p \times p$$ کاهش دهد بطوری که $$p$$ بسیار کوچکتر از $$n$$ باشد.

متاسفانه پایداری پیش‌بینی‌ها با افزایش نقاط آموزشی یا انتخاب آن‌ها تغییر می‌کند. اگر نقاطی که در مجموعه آموزشی به شکل مناسبی انتخاب نشده باشند، محاسبات GP باعث ایجاد خطا و اشتباهات زیادی در برآورد می‌شود. در تصویر زیر مدل‌سازی توسط GP را با ۱۶ نقطه آموزشی می بینید که در عمل واقعا قادر به پیش‌بینی منحنی آبی رنگ نیست.

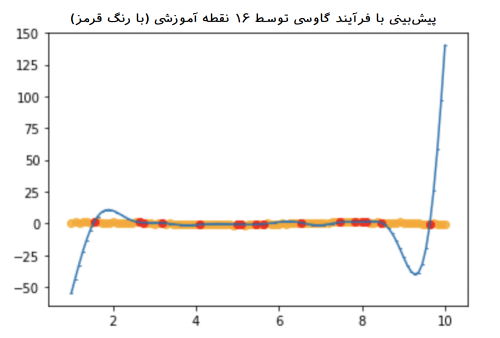
از طرفی با توجه به اینکه روش GP را به عنوان یک روش ناپارمتری در نظر گرفتیم ولی خطای برآورد برای مقدارهای $$y^*$$ و $$y$$ها از توزیع نرمال پیروی می‌کند. از طرفی با توجه به اطلاعات پیشینی که از توزیع خطاها ممکن است داشته باشیم، این امر می‌تواند باعث بهبود برآوردها شود ولی اگر این اطلاع با واقعیت مطابقت نداشته باشد، خطای برآوردها زیاد خواهد بود. برای مثال اگر داده‌ها فقط مقدارهای مثبت داشته باشند یا در یک بازه خاصی تغییر کنند، انتخاب توزیع نرمال به عنوان توزیع پیشین مناسب به نظر نمی‌رسد.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• مجموعه آموزش های داده کاوی یا Data Mining در متلب
• مهم‌ترین الگوریتم‌های یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
• رگرسیون لاسو (Lasso Regression) — به زبان ساده
• رگرسیون خطی با متغیرهای طبقه‌ ای در SPSS — راهنمای گام‌ به‌ گام

^^