روش تفاضل محدود (Finite Difference Method) – از صفر تا صد
در مطالب قبلی وبلاگ فرادرس، پیوستگی و بقای جرم، مومنتوم خطی و زاویهای و معادلات ناویر استوکس مورد بررسی قرار گرفتند. همانطور که بیان شد این روابط و قوانین بقا، کاربرد بسیار زیادی در مسائل مختلف مکانیک سیالات مانند دینامیک سیالات محاسباتی دارند. در این مطالب به خوبی نشان داده شد که بعد از نوشتن این روابط و قوانین بقا، در نهایت ما به مجموعهای از معادلات دیفرانسیل با مشتقات جزئی میرسیم و این معادلات با استفاده از روشهای عدد مختلفی مانند روش تفاضل محدود و روش حجم محدود قابل حل هستند.
در واقع روش تفاضل محدود، به منظور محاسبه مشتقهای جزئی، محیط و دنیای پیوسته پیرامون ما را به محیط گسسته تبدیل میکند. این مطلب به صورت دقیق به بررسی حل معادلات دیفرانسیل با مشتقات جزئی با استفاده از روش تفاضل محدود میپردازد. بنابراین در ابتدا مفهوم تقریب تفاضل محدود و شیوه محاسبه آن مورد بررسی قرار میگیرد. سپس پارامتر مهم خطای برشی معرفی میشود و همچنین روابط حاکم بر تقریب تفاضل محدود در مراتب بالاتر و حالت چند بعدی نیز مورد مطالعه قرار میگیرند. در ادامه مفهوم روش تفاضل محدود و شیوه استفاده از آن به کمک یک مثال و به صورت دقیق بیان میشود و در انتهای مطلب نیز شرایط مرزی در مسائل دینامیک سیالات محاسباتی بررسی میشوند. توجه کنید که مطالعه پایداری روش تفاضل محدود نیز اهمیت بسیار زیادی در استفاده از این روش عددی دارد که در مطلب «پایداری روش تفاضل محدود» مورد مطالعه قرار گرفته است.
تقریب تفاضل محدود
در مطالب قبلی وبلاگ فرادرس، معادلات دیفرانسیل معمولی (Ordinary Differential Equation) به صورت دقیق و با استفاده از تقریب سری تیلور مورد بررسی قرار گرفتند. این تقریب برای مشتق در زمان نوشته شد. با استفاده از این روش، تقریبی برای مشتق U بر حسب زمان و در زمان n به دست آمد که این تقریب با نماد زیر نشان داده میشود.
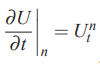
این تقریب با استفاده از مقادیر در زمانهای قبل و بعد یعنی به دست آمد. ایده اصلی موجود در روش تفاضل محدود برای معادلات دیفرانسیل با مشتقات جزئی نیز بسیار مشابه با روش بالا است با این تفاوت که در روش تفاضل محدود به جای زمان با مکان سر و کار داریم و معادلات را در مکانهای گسسته بازنویسی میکنیم. مکانهای گسسته و مشتقات جزئی در دو رابطه زیر به صورت خلاصه بیان شدهاند.
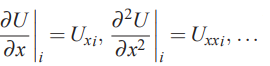
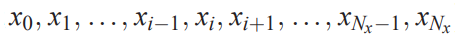
بنابراین همانطور که در ابتدای مطلب اشاره شد، با استفاده از روش تفاضل محدود میتوان یک محیط پیوسته را به محیط گسسته تبدیل کرد و بازنویسی معادلات و محاسبه مشتقهای جزئی را در آن انجام داد. فواصل نقاط مختلف گسسته شده در روش تفاضل محدود برابر با در نظر گرفته میشود (این فواصل میتوانند با یکدیگر برابر یا متفاوت باشند) و شکل زیر به خوبی یک «شبکه» (Mesh) و ساختار یک بعدی برای تقریب تفاضل محدود را به تصویر کشیده است.
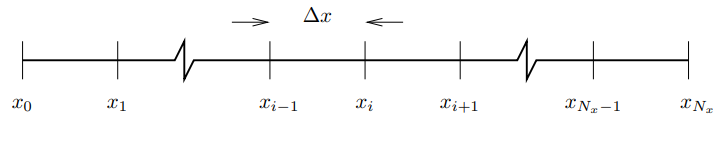
در ادامه هدف ما محاسبه یک تقریب تفاضل محدود برای در نقطه است. برای یک تابع مشتقپذیر U، مشتق جزئی در نقطه را میتوان با استفاده از رابطه زیر مورد محاسبه قرار داد.
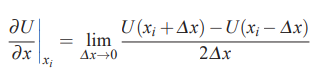
توجه کنید که تقریب تفضل محدود، زمانی حاصل میشود که عبارت حد در رابطه بالا حذف شود. در این حالت، مشتق جزئی U در راستای x و در نقطه i برابر با عبارت سمت راست معادله در نظر گرفته میشود. این موضوع در رابطه زیر به خوبی نشان داده شده است.
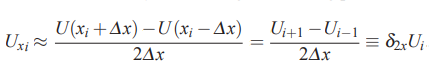
این روش به نام روش «تفاضل مرکزی» (Central Difference) معروف است و به عملگر δ2x، «عملگر تفاضل مرکزی» (Central Difference Operator) گفته میشود.
مشکل اصلی روش تفاضل محدود مرکزی این است که وقتی مقدار U در و با یکدیگر برابر باشند، مشتق در نقطه را برابر با صفر محاسبه میکند. این در حالی است که در بسیاری از توابع نوسانی این گونه نیست و مشتق مقداری مثبت یا منفی دارد. بنابراین از روشهایی با مراتب بالاتر و یا روشهای «یک طرفه» (One-Side) نیز برای محاسبه مشتق جزئی استفاده میشود. برای مثال یک «تقریب تفاضل پسرو» (Backward Difference Approximation) به صورت زیر قابل بیان است.
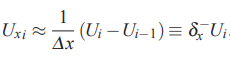
مشابه روابط بالا، میتوان تفاضل پیشرو را نیز برای محاسبه مشتق بیان کرد. بنابراین تقریب تفاضل پیشرو برای مشتق جزئی تابع U در راستای x و در نقطه i به شکل زیر محاسبه میشود.
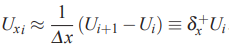
خطای برشی تقریب تفاضل محدود
در این بخش مفهوم «خطای برشی» (Truncation Error) در روش تفاضل محدود مورد بررسی قرار میگیرد. این خطای برشی، مرتبه دقت روش مورد استفاده را نشان میدهد و به عنوان یک معیار برای انتخاب روش عددی مناسب بر اساس سرعت حل در دینامیک سیالات محاسباتی شناخته میشود. بنابراین در ادامه نمونهای از شیوه محاسبه خطای برشی برای روشهای مختلف تفاضل محدود با جزئیات مورد مطالعه قرار میگیرد.
فرض کنید که برای محاسبه مشتق اول در نقطه i، از تفاضل پسرو استفاده میشود. خطای برشی این روش را میتوان با استفاده از سری تیلور محاسبه کرد. در واقع ابتدا رابطه تفاضل پسرو را مینویسیم. در ادامه با استفاده از سری تیلور یکی از عبارتها را بازنویسی میکنیم. بدین ترتیب خطای برشی موجود در روش مورد استفاده محاسبه میشود. این روند در روابط زیر به خوبی بیان شده است.
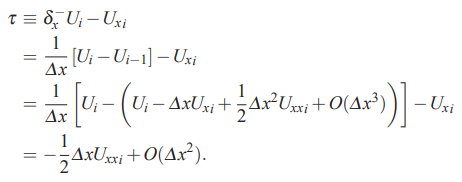
روند مشابه روابط بالا را میتوان برای سایر روشها یعنی روش تفاضل پیشرو و مرکزی و همچنین تفاضل محدود مراتب بالاتر نیز اجرا کرد.
تقریب تفاضل محدود برای مشتقهای مراتب بالاتر
تا به اینجا، روشهای مختلفی برای محاسبه تقریب تفاضل محدود و برای محاسبه مشتق اول نوشته شد. توجه شود که یکی از اهداف بسیار مهم ما در این قسمت، حل معادلات دیفرانسیل با مشتقات جزئی است و در این معادلات، معمولا مشتقات مراتب بالاتر مانند Uxxx ،Uxx حضور دارند.
در قسمتهای قبل نشان داده شد که محاسبه تقریب تفاضل محدود برای مشتق اول، با استفاده از تعریف مشتق قابل بیان است. در این قسمت نیز برای محاسبه تقریب تفاضل محدود مشتقهای مراتب بالاتر ابتدا تعریف مشتق را برای آنها مینویسیم و در ادامه رابطه نهایی آن را محاسبه میکنیم. این موضوع در روابط زیر و برای محاسبه تقریب تفاضل محدود مشتق دوم به خوبی مورد بررسی قرار گرفته است.

در ادامه برای محاسبه تقریب تفاضل محدود مشتق دوم، علامت حد را حذف میکنیم. بنابراین داریم:
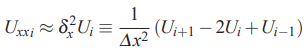
به صورت کلی میتوان بیان کرد که محاسبه تقریب تفاضل محدود مشتقات جزئی با استفاده از روندی که در بالا توضیح داده شد، یعنی استفاده از تعریف مشتق برای محاسبه تقریب تفاضل محدود، کاری بسیار خسته کننده است. در واقع در تمامی مسائل ما به دنبال تعریف یک تقریب تفاضل محدود با استفاده از تعدادی نقاط هستیم که خطای برشی آن کمترین مقدار ممکن باشد. بنابراین برای سادگی محاسبه این تقریب تفاضل محدود، یک حالت کلی برای تقریب تفاضل محدود به شکل زیر در نظر بگیرید.
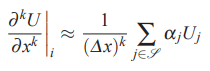
در این رابطه αj ضرایب موجود در تقریب تفاضل محدود را نشان میدهند. علامت موجود در زیر سیگما ( ) نیز مجموعه نقاطی را نشان میدهد که قرار است با استفاده از آنها تقریب تفاضل محدود را بنویسیم. برای مثال، تقریب تفاضل مرکزی یعنی شامل سه نقطه است که مقدار متغیر U در این سه نقاط به ترتیب برابر با ، و هستند.
بنابراین همانطور که در بالا توضیح داده شد، معادلات و تقریبهای مختلف تفاضل محدود با در نظر گرفتن مجموعه نقاط مختلف محاسبه میشود. شیوه استفاده از نقاط مختلف برای نوشتن تقریب تفاضل محدود در مثال زیر به صورت دقیق مورد بررسی قرار گرفته است. با استفاده از روشی که در این مثال بیان شده، سایر تقریبهای تفاضل محدود برای مشتقهای جزئی در ریاضیات و دینامیک سیالات محاسباتی قابل محاسبه است.
مثال
تقریب تفاضل محدودی برای محاسبه مشتق جزئی مرتبه اول با استفاده از چهار نقطه بنویسید.
در این قسمت برای محاسبه تقریب تفاضل محدود مشتق مرتبه اول از چهار نقطه ، ، و استفاده میشود. بنابراین در ابتدا بسط تیلور برای این چهار نقطه را به صورت زیر مینویسیم.
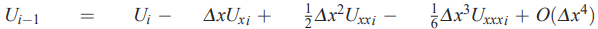
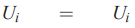
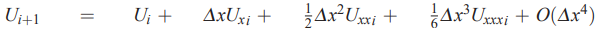
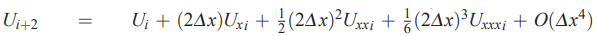
در ادامه و با استفاده از رابطهای که در ابتدای بخش «تقریب تفاضل محدود برای مشتقهای مراتب بالاتر» بیان شد، تقریب تفاضل محدود را مینویسیم. بنابراین داریم:
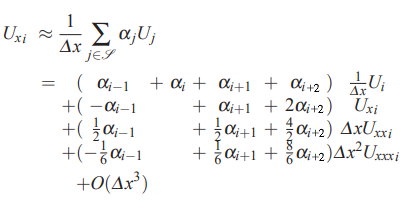
بنابراین با توجه به روابطی که در بالا ارائه شد، 4 ضریب مجهول در تفاضل محدود این عبارت حضور دارند. این چهار ضریب مجهول به ترتیب ، ، و هستند.
در ادامه، ضرایب را طوری انتخاب میکنیم که ضریب Uxi برابر با ۱ و ضرایب سایر موارد موجود یعنی Ui، Uxxi و Uxxxi برابر با صفر باشد. بنابراین چهار معادله و چهار مجهول موجود است که میتوان این دستگاه معادلات را به فرم ماتریس زیر بیان کرد.
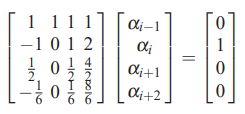
پاسخ این دستگاه معادلات با استفاده از روشهای مختلف قابل محاسبه است و در نهایت مقدار هرکدام از ضرایب به صورت زیر در میآید.
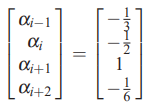
بر این اساس با قرار دادن ضرایب بالا در معادله اولیه، تقریب تفاضل محدود با دقت مرتبه سه برای نقاط ، ، و به شکل زیر در میآید.
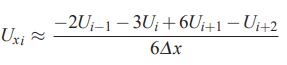
روشی که در این قسمت با جزئیات مورد بررسی قرار گرفت را میتوان برای محاسبه تمام مشتقات جزئی و با دقتهای مختلف (خطای برشی) مورد استفاده قرار داد و مسائل گسستهسازی گوناگون موجود در مکانیک سیالات و دینامیک سیالات محاسباتی را با استفاده از آن محاسبه کرد. توجه کنید که این روابط در مکانیک سیالات اهمیت بسیار زیادی دارند. زیرا معادلات ناویر استوکس شامل ترمهای غیر خطی هستند و برای محاسبه آنها حتما باید از روشهای عددی مختلف مانند روش تفاضل محدود استفاده کرد.
پیشنهاد ما این است که یک دور مسئله بالا را خودتان حل کنید و نتیجه آن را با حل ارائه شده در این قسمت مقایسه کنید و بعد از آن و برای تمرین بیشتر، تقریب تفاضل محدود را برای مشتق سوم در نقطه i یعنی Uxxxi با استفاده از 5 نقطه ، ، ، و بنویسید. در نهایت خطای برشی و دقت رابطه به دست آمده را محاسبه کنید.
توجه کنید که تا به اینجا، تقریب تفاضل محدود را برای مسائل یک بعدی مورد بررسی قرار دادیم. در بخش بعد این تقریب را برای حالت دو بعدی تکرار میکنیم و مفاهیم و روابط آن را مورد مطالعه قرار میدهیم.
تقریب تفاضل محدود در حالت دو بعدی
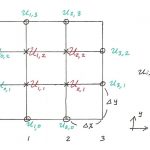
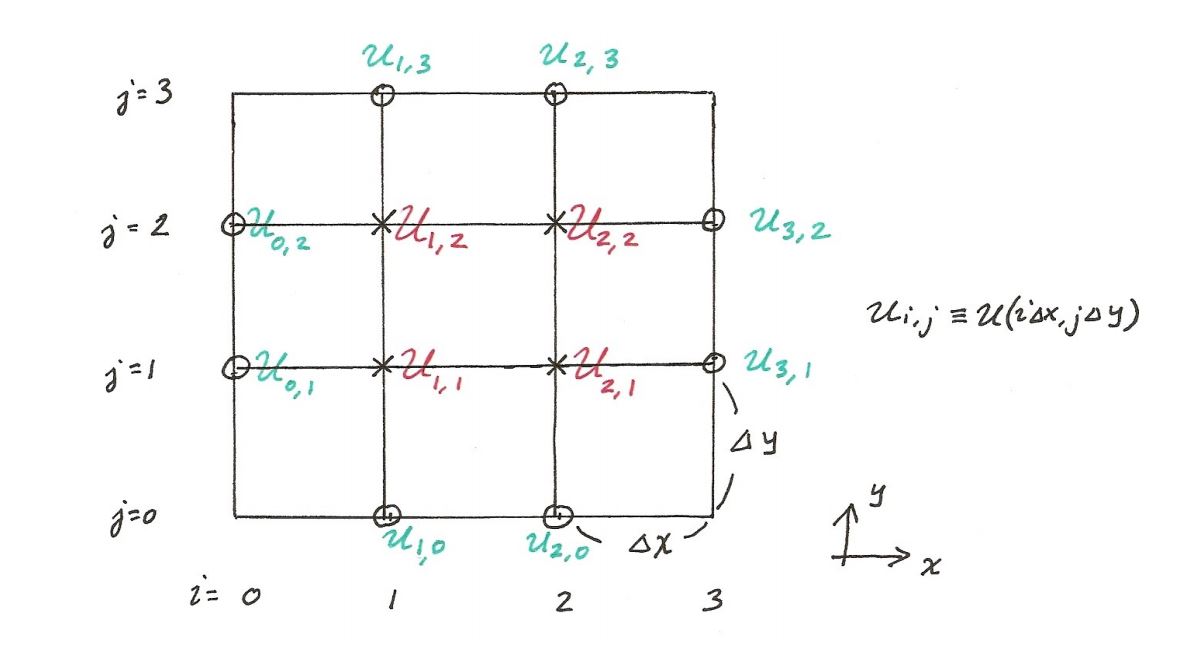
مشابه روندی که در بالا طی شد، ما میتوانیم مفهوم تقریب تفاضل محدود را به فضا و حالات دو بعدی و سه بعدی نیز تعمیم دهیم. بنابراین در حالت دو بعدی و تحت شرایط ذکر شده، ساختار و شبکه حل مورد نظر خود را به شکل زیر نمایش میدهیم.
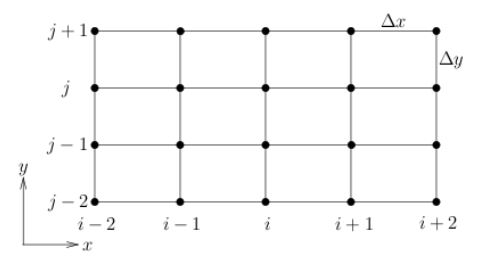
پارامتری مانند U را در نظر بگیرید که مقدار آن در مختصات (i, j) با Ui,j نشان داده میشود. در این شرایط، تقریب تفاضل مرکزی برای مشتق مرتبه اول در راستای x و y را میتوان با استفاده از رابطه زیر نمایش داد.
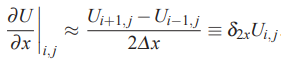
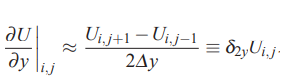
نکته مهمی که باید به آن اشاره کرد این است که مجموعه نقاطی که در تفاضل محدود دو بعدی و سه بعدی در نظر گرفته میشود شامل نقاطی است که در اطراف Ui,j قرار دارند.
تا به اینجا، تقریب تفاضل محدود مورد بررسی قرار گرفت و شیوه محاسبه آن برای مشتق مرتبه اول و مراتب بالاتر نشان داده شد. همچنین شیوه نمایش و محاسبه مشتق در دو بعد نیز مورد بررسی قرار گرفت.
در ادامه به بررسی «روش تفاضل محدود» (Finite Difference Method) پرداخته میشود. برای استفاده از این روش نیاز به داشتن دانش کافی در زمینه قوانین و روابط مختلف حاکم بر سیالات در علم دینامیک سیالات محاسباتی داریم. این قوانین و روابط از جمله پرکاربردترین قوانین موجود در مکانیک سیالات هستند و قوانین پیوستگی و بقای جرم، مومنتوم خطی و زاویهای و معادلات ناویر استوکس را در بر میگیرند.
روش تفاضل محدود
معادله یک بعدی «نفوذ و جابهجایی» (Convection-Diffusion) را در نظر بگیرید. این معادله را میتوان به شکل زیر بیان کرد.
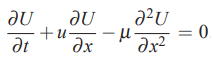
در ادامه این معادله را با استفاده از تقریب تفاضل محدود، گسستهسازی میکنیم. برای این منظور از عملگر تفاضل محدود مرکزی استفاده میشود و در نهایت رابطه فوق به شکل زیر در میآید.
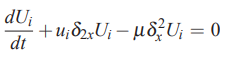
رابطه فوق یک معادله دیفرانسیل معمولی (توجه کنید که علامت ∂ به d تبدیل شده) برای Ui را نشان میدهد و شامل مقادیر U در نقاط ، و میشود.
توجه شود که معادله دیفرانسیل معمولی، معادلهای است که در آن، متغیر مسئله تنها به یک پارامتر مستقل، وابسته است و علامت مشتق با d نشان داده میشود. همچنین معادله دیفرانسیل با مشتقات جزئی به معادلهای گفته میشود که متغیر آن به چند پارامتر مستقل، وابسته باشد و علامت مشتق با نماد ∂ (مشتق جزئی) نشان داده میشود.
در ادامه مقادیر پارامتر U در تمامی نقاط شبکه را با استفاده از یک بردار به شکل زیر نمایش میدهیم.
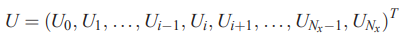
در نهایت این معادلات به صورت مجموعهای از معادلات دیفرانسیل معمولی در میآیند که میتوان آنها را به شکل خلاصه شده زیر نمایش داد.
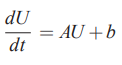
در این رابطه، پارامتر b، شرایط مرزی را نمایش میدهد. شرایط مرزی در واقع پارامترهای معلوم مسئله در مرزها را مشخص میکنند. برای مثال ممکن است سرعت جریان سیال در ورودی یک لوله معلوم باشد یا دمای دیواره لوله مقدار مشخص و ثابتی داشته باشد. در این شرایط، سرعت ورودی و دمای دیواره به عنوان دو شرط مرزی در نظر گرفته میشوند.
در رابطه بالا، ماتریس A را میتوان به شکل زیر نمایش داد.
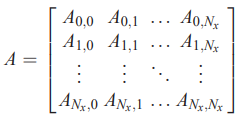
توجه کنید که سطر i ام ماتریس بالا، ضرایب مربوط به معادله دیفرانسیل معمولی پارامتر U در نقطه i را نشان میدهند. نکته مهم دیگری که باید به آن اشاره کرد این است که به غیر از حالاتی که در آنها شرایط مرزی حضور دارد، مقدار Ai,j ضریب αj موجود در تقریب تفاضل محدود را نمایش میدهد.
به عنوان مثال برای یک تقریب تفاضل مرکزی، ضرایب به صورت زیر در میآیند.
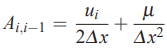
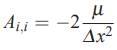
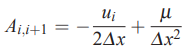
بنابراین زمانی که از تفاضل مرکزی برای گسستهسازی معادله نفوذ جابهجایی یک بعدی استفاده میشود، سطر i ام تنها شامل سه ضریب بالا است و باقی ضرایب در سطر i ام برابر با صفر در نظر گرفته میشوند. به صورت کلی میتوان بیان کرد که تعداد عبارات صفر در هر سطر به تعداد نقاطی بستگی دارد که با استفاده از آنها تقریب تفاضل محدود را بیان میکنیم.
رابطه زیر که در بالا نیز مورد مطالعه قرار گرفت را دوباره در نظر بگیرید.
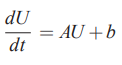
این رابطه به صورت نیمه گسسته است. زیرا گسسته سازی تنها در مکان انجام شده و در زمان از تقریب تفاضل محدود استفاده نشده است. برای اینکه معادله نفوذ و جابهجایی ارائه شده را به صورت عددی حل کنیم، لازم است که گسسته سازی آن را به صورت کامل انجام دهیم. برای این منظور، با استفاده از روشهایی که در معادلات دیفرانسیل معمولی بیان کردیم سمت چپ معادله فوق را گسسته میکنیم. برای مثال در صورتی که از روش اویلر پیشرو ساده استفاده کنیم، معادله فوق به شکل زیر در میآید.
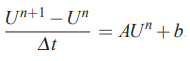
استفاده از روش تفاضل محدود مرکزی برای بیان مشتقات مکانی و روش اویلر پیشرو برای بیان مشتقات زمانی یکی از رایجترین، پرکاربردترین و معروفترین روشهای موجود در تفاضل محدود و دینامیک سیالات محاسباتی را نتیجه میدهد. این روش به روش «زمان پیش رو و مکان مرکزی» (Forward Time Central Space) معروف است. در محاسبات عددی و CFD این روش را به صورت اختصاری با نماد FTCS نمایش میدهند.
توجه کنید که این رابطه یک رابطه صریح است و نیاز به بیان پارامتر A به صورت صریح نیست. نکته دیگر این است که برای اصلاح جواب در نقطه i در هر زمان، به شکل زیر عمل میکنیم.
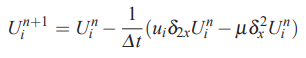
مثال
رابطه جابهجایی یک بعدی را در نظر بگیرید. در صورتی که روش تفاضل محدود روی این معادله اعمال شود. حل عددی آن را میتوان به شکل زیر محاسبه کرد.
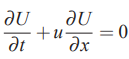
برای گسسته سازی معادله بالا، از روش تقریب تفاضل مرکزی برای مشتق مکانی و اویلر پیش رو برای مشتق زمانی استفاده میشود. این موضوع در رابطه زیر نشان داده شده است.
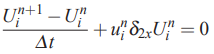
توجه کنید که این حالت همان روش زمان پیش رو و مکان مرکزی که در بالا ارائه شد را نشان میدهد و تنها تفاوت آن این است که ترم نفوذ یا دیفیوژن در آن حذف شده است. در ادامه و برای حل عددی این رابطه، شرط اولیه را برابر با رابطه زیر در نظر میگیریم.
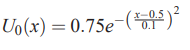
در این مثال، ناحیه حل را برای تولید شبکه در محدود 0 تا ۱ و شرایط مرزی را پریودیک در نظر میگیریم. کد متلب این مثال در ادامه آورده شده است.
نتایج این حل با استفاده از روش تفاضل محدود در شکلهای زیر برای زمان t=0.5 ، t=0.25 و t=1.0 به تصویر کشیده شده است.
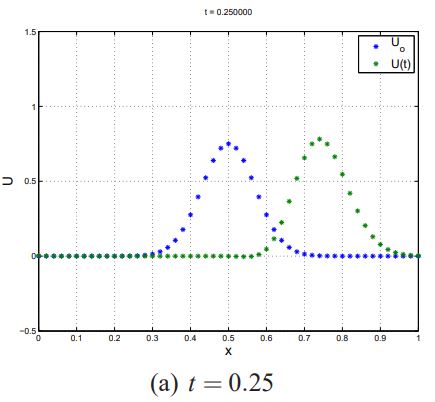
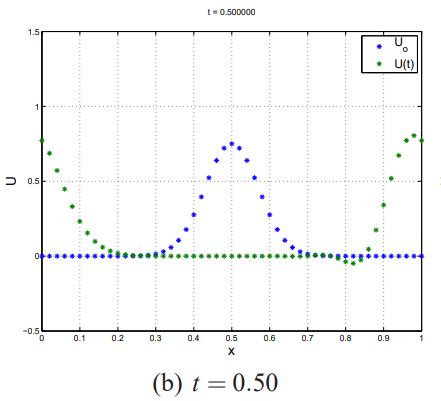
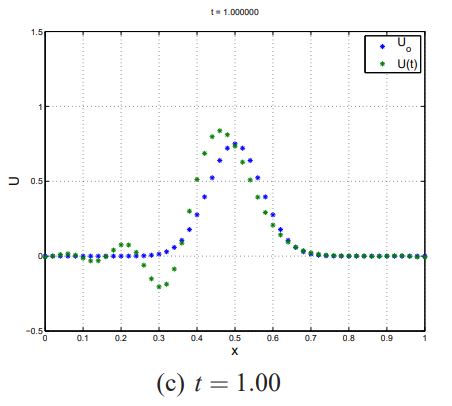
در مباحث بعدی وبلاگ فرادرس نشان داده میشود که الگوریتم FTCS برای هر مقداری از Δt برای معادله «جابهجایی خالص» (Pure Convection) ناپایدار است. این موضوع در این مثال نیز به خوبی نشان داده شده است.
شرایط مرزی
در این بخش، پیاده سازی و اجرای روش تفاضل محدود را روی مرزها مورد بررسی قرار میدهیم. توجه کنید که بررسی تمام شرطهای مرزی در یک مطلب دیگر در وبلاگ فرادرس که مرتبط با دینامیک سیالات محاسباتی و روشهای عددی است به صورت دقیق مورد بررسی قرار میگیرد و در مطلب حاضر تنها شرط مرزی دریکله مطالعه میشود.
شرط مرزی دریکله، شرطی است که در آن، حالت مطلوب در مرز مشخص شده است. برای مثال شرط مرزی دریکله در یک مسئله انتقال حرارت، دما را در مرز ناحیه حل مشخص میکند.
به عنوان مثال دیگر برای شرط مرزی دریکله، یک مسئله یک بعدی نفوذ و جابهجایی را در نظر بگیرید. در این مسئله سرعت ورودی به عنوان شرط مرزی دریکله معرفی میشود. بنابراین برای حل تفاضل محدود، مقدار سرعت را در ورودی برابر با مقداری ثابت در نظر میگیریم و معادلات را در نقاط میانی میدان حل بررسی میکنیم.
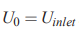
رابطه بالا، سرعت را در نقطه و «نود» (Node) یا گره اول یعنی i=0 نشان میدهد. این نود، مرز ورودی را نشان میدهد. توجه کنید که در حلهای عددی نقاط موجود در شبکه و مش حل را نود یا گره مینامند.
در مسئله یک بعدی نفوذ و جابهجایی که در ابتدای این بخش بیان شد، گسسته سازی در نقطه اول یعنی i=1 با روش تفاضل مرکزی انجام میشود. در نهایت این تقریب تفاضل مرکزی، به شکل زیر در میآید.
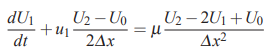
در ادامه و با توجه به آنکه مقدار U0 معلوم و ثابت (شرایط مرزی دریکله) است، مقدار آن را در رابطه بالا جایگذاری میکنیم و در نهایت رابطه تفاضل محدود به شکل زیر در میآید.
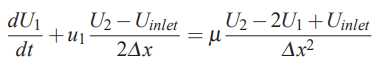
در قسمت قبل و در مسیر اجرای یک حل عددی دیدیم که ما مجهولات مسئله که در اینجا سرعت است را به صورت یک بردار نشان میدهیم. بنابراین در حالتی که شرط مرزی دریکله داریم، یکی از اجزای این بردار که مقدار سرعت در مرز را نشان میدهد، معلوم است. بنابراین در این شرایط، بردار مجهولات را به شکل زیر نمایش میدهیم.
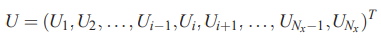
یکی دیگر از موارد بسیار مهم در مسیر اجرای یک حل عددی تعیین پارامتر b در رابطه ۲۴ است. در واقع در مسائلی که شرط مرزی دریکله در آن به کار رفته، پارامتر b مقدار شرط مرزی را نیز در بر میگیرد. برای مثال رابطه بازنویسی شده به وسیله شرایط مرزی در مسئله نفوذ و جابهجایی (رابطه ۳۷) در نظر بگیرید. در این رابطه مقدار b را میتوان به شکل زیر محاسبه کرد.
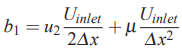
سایر شرطهای مرزی مانند شرط مرزی نیومن و کوشی در سایر مطالب وبلاگ فرادرس به صورت دقیق مورد بررسی قرار میگیرد.
بنابراین همانطور که اشاره شد، روش تفاضل محدود، به منظور محاسبه مشتقهای جزئی، محیط و دنیای پیوسته پیرامون ما را به محیط گسسته تبدیل میکند و با تعریف گره و شبکه حل در حالت یک بعدی دو بعدی و سه بعدی، میتوان حل عددی معادلات دیفرانسیل با مشتقات جزئی موجود در ریاضیات و دینامیک سیالات محاسباتی را با روش تفاضل محدود مورد مطالعه قرار داد.
این مطلب به صورت دقیق به بررسی حل معادلات دیفرانسیل با مشتقات جزئی با استفاده از روش تفاضل محدود پرداخت. در ابتدای این مطلب مفهوم تقریب تفاضل محدود و شیوه محاسبه آن مورد بررسی قرار گرفت. سپس پارامتر مهم خطای برشی معرفی شد و همچنین روابط حاکم بر تقریب تفاضل محدود در مراتب بالاتر و حالت چند بعدی نیز مورد مطالعه قرار گرفت. در ادامه مطلب مفهوم روش تفاضل محدود و شیوه استفاده از آن به کمک یک مثال و به صورت دقیق بیان شد و در انتهای مطلب نیز شرایط مرزی در مسائل دینامیک سیالات محاسباتی به صورت دقیق مورد مطالعه شد. توجه کنید که «پایداری روش تفاضل محدود» و «روش حجم محدود (Finite Volume Method)» نیز از جمله مطالب بسیار مهم در علم مکانیک هستند که در مطالب دیگر وبلاگ فرادرس به صورت دقیق مورد مطالعه قرار گرفتهاند.
در صورتی که به مباحث ارائه شده، علاقهمند هستید و قصد یادگیری در زمینههای مطرح شده در مکانیک سیالات را دارید، آموزشهای زیر به شما پیشنهاد میشود:
- دینامیک سیالات محاسباتی (CFD) — از صفر تا صد
- معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد
- پایداری روش تفاضل محدود — به زبان ساده
- آیرودینامیک (Aerodynamics) چیست؟ — از صفر تا صد
- پیوستگی و بقای جرم در سیالات — از صفر تا صد
- مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد
- توربوماشین (Turbomachinery) — به زبان ساده
^^












سلام تشکر فراوان از مطالب
بهتر است فایل پی دی اف نیز کنار کار باشد مانند میکی پدیا که تمام مطالب به همراه پی دی اف موجود است
ممنون بابت توضیحات خلاصه و مفیدتون. مطمئناً وجود سایت هایی ازین دست منجبر به افزایش سطح علمی دانشجویان خواهد شد.
سلام. باز هم مثل دیگر آموزش های فرادرس بسیار مفید و عالی بود. با تشکر از مجموعه و پرسنل فرادرس.