موج الکترومغناطیسی چگونه ایجاد می شود؟ — آموزش جامع

پیش‌تر در مبحث امواج الکترومغناطیسی عنوان شد که امواج تخت در فضای خلاء، با سرعت نور منتشر می‌شوند. در ادامه در مورد نحوه ایجاد و انتشار این امواج بحث خواهیم کرد. هم‌چنین محاسبات مربوط اندازه و نحوه انرژی منتشر شده توسط آن‌ها را تشریح خواهیم کرد. این مبحث به این دلیل مطرح شد که در اکثر متون علمی در مورد نحوه انتشار امواج الکترومغناطیسی بحث شده؛ این در حالی است که کمتر به نحوه ایجاد این امواج پرداخته شده است.

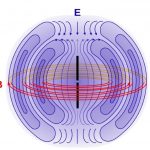
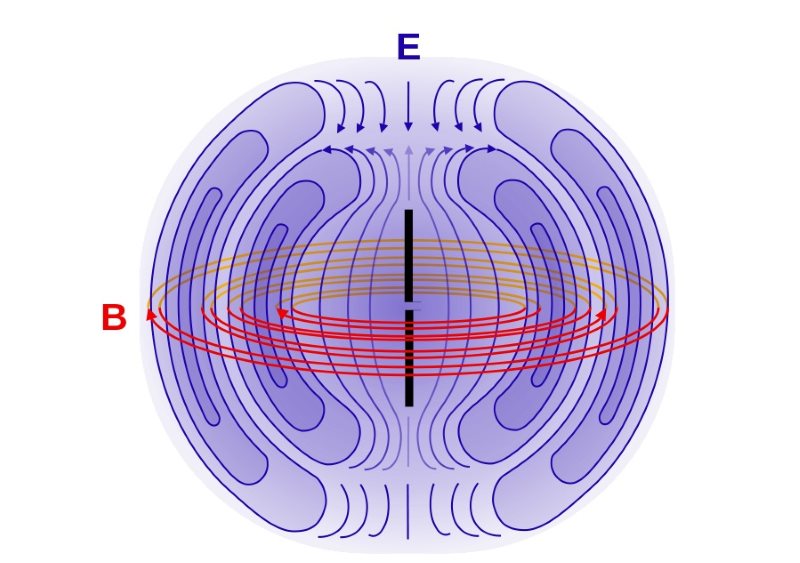
امواج الکترومغناطیسی، کاربرد بسیاری در تکنولوژی دارند. در حقیقت می‌توان با استفاده از آن‌‌ها اطلاعات را منتقل کرد. یکی از آشناترین و ساده‌ترین ابزار تولید کننده موج الکترومغناطیسی آنتن است. شکل زیر شماتیک آنتنی را نشان می‌دهد که با جابجایی بار الکتریکی، موجی الکترومغناطیسی را تولید کرده.

مقدمه

ویژگی‌های یک موج الکترومغناطیسی نیز دقیقا مشابه با موج مکانیکی است؛ در نتیجه جهت درک بهتر روابط مربوط به امواج الکترومغناطیسی می‌توان از تشابه آن‌ها با امواج مکانیکی بهره برد. برای نمونه به‌منظور تولید موج مکانیکی روی یک طناب، یک سمت آن را نوسان داده و در نتیجه آن موجی مکانیکی روی آن تشکیل خواهد شد. در حقیقت ما کاری خلاف جهت کشش موجود در طناب انجام داده‌ایم و در نتیجه آن شار انرژی در طناب منتقل می‌شود. امواج الکترومغناطیسی نیز به همین صورت هستند. در آن‌ها میدان الکتریکی همان طناب است و با دادن جابجایی اولیه (یا همان اغتشاش اولیه)، نیرویی در میدان بوجود می‌آید که بر خلاف نیروی کشش عمل می‌کند. از این رو موجی بوجود خواهد آمد که در راستای خط میدان الکتریکی منتشر خواهد شد.

پیشنهاد می‌شود قبل از مطالعه ادامه مطلب،‌ مباحث امواج الکترومغناطیسی و معادلات ماکسول را مطالعه فرمایید.

ایجاد موج

چگونه می‌توان یک خط میدان الکتریکی را هم‌چون طناب جابجا کرد؟ هما‌ن‌گونه که پیش‌تر نیز بیان شد، جهت تولید یک موج مکانیکی بایستی نقطه‌ای از طناب جابجا شود؛ در مورد امواج الکترومغناطیسی نقاط مذکور به‌صورت بارهایی الکتریکی هستند که خطوط میدان الکتریکی به آن‌ها متصل شده است. از این رو با جابجایی این بار‌ها می‌توان میدان الکتریکی را نوسان داد و در نتیجه آن موجی الکترومغناطیسی ایجاد خواهد شد. با دانستن این موضوع و هم‌چنین فهمیدن این‌که امواج الکترومغناطیسی در خلا با سرعت نور منتشر می‌شوند، می‌توان معادلات مربوط به تحریک اولیه، جهت تولید موج الکترومغناطیسی را بدست آورد.

جهت توصیف نحوه ایجاد تحریک اولیه میدان الکتریکی، فرض کنید که مطابق با شکل زیر بستری باردار، با چگالی σ در صفحه yz قرار گرفته است.

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

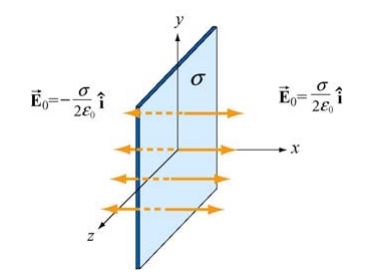
با استفاده از قانون گاوس، می‌دانیم که میدان الکتریکی اطراف این صفحه برابر با مقدار زیر است.

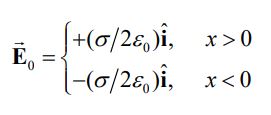
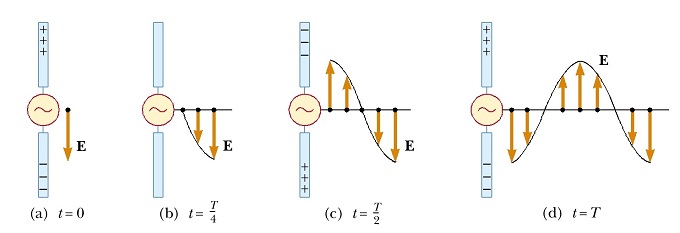
حال تصور کنید که در زمان t=0 صفحه را با سرعت ثابت $$\overrightarrow{v}=-\nu \widehat{j}$$ به سمت پایین حرکت می‌دهیم. در این‌ لحظه هدف ما بررسی شرایط در زمان t=T است. جهت بررسی تغییرات در ابتدا به شکل خطوط میدان ارائه شده در تصاویر زیر توجه کنید. این تصاویر مربوط به خطوط میدان الکتریکی در زمان t=T و t=0 هستند.

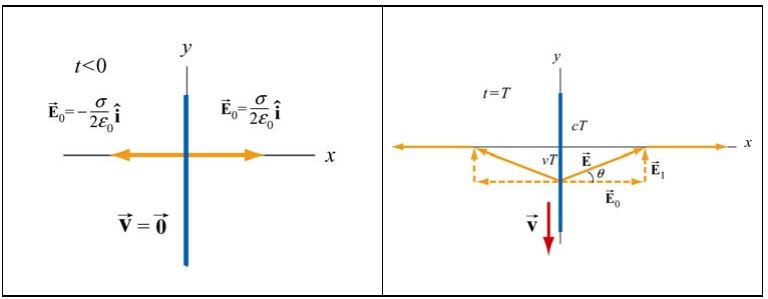
همان‌طور که در شکل فوق نیز نشان داده شده، در حالت سکون (t<0)، پایه‌ی بردار میدان الکتریکی روی صفحه قرار گرفته است. با حرکت دادن صفحه به سمت پایین، این پایه نیز به همراه آن حرکت خواهد کرد. بنابراین در لحظه t=T، این پایه در مختصات y=-vT قرار دارد. فرض شده که اطلاعات با سرعت نور در راستای محور x منتشر می‌شوند. از این رو بخشی از میدان الکتریکی که در x>cT قرار گرفته، از حرکت بار‌ها در x=0 اطلاعاتی نخواهد داشت؛ یا به بیانی دیگر در لحظه t=T در x|>CT| اتفاقی رخ نداده است.

همان‌گونه که در شکل بالا نیز مشخص شده، پایه میدان الکتریکی به‌صورت خطی، در راستای محور x کاهش می‌یابد. این پدیده دقیقا مشابه با تولید موج مکانیکی در یک طناب است. در این مسئله نیز با جابجا کردن صفحه باردار به سمت پایین،‌ میدان الکتریکی $$\overrightarrow{E}_0$$ به اندازه $$\overrightarrow{E}_1$$ تغییر خواهد کرد. در نتیجه میدان جدید ایجاد شده در فاصله $$0\enspace<\enspace |x|\enspace<\enspace cT$$ برابر است با:

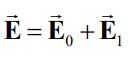
همان‌طور که در تصویر سمتِ چپِ شکل ۱ نشان داده شده، میدان الکتریکی $$\overrightarrow{E}$$ بایستی موازی با پایه خط میدان الکتریکی در $$|x|=cT$$ باشد. در نتیجه زاویه $$\theta$$ در شکل ۱ را می‌توان مطابق با عبارت زیر بدست آورد.

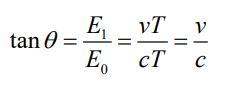
در رابطه بالا $$E_0=|\overrightarrow{E}_0|$$ و $$E_1=|\overrightarrow{E}_1|$$ به‌ترتیب اندازه میدان الکتریکی قبل و بعد از اعمال تحریک است. از طرفی θ، زاویه بین $$\overrightarrow{E}_1$$ با محور x را نشان می‌دهد. با استفاده از رابطه بالا، میدان $$\overrightarrow{E}_1$$ را می‌توان مطابق با رابطه زیر بدست آورد.

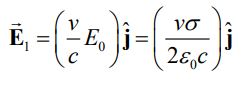
از مبحث میدان الکتریکی نیز می‌دانیم که میدان الکتریکی برابر با $$E_0 \enspace = \enspace \sigma/2 \epsilon_0$$ است. رابطه ۱ بیان‌کننده وابستگی میدان الکتریکی ایجاد شده ناشی از سرعت v است. جهت بردار $$\overrightarrow{E}_1$$ معادل با نیرویی است که به بار‌های قرار گرفته روی سطح وارد می‌شود و در مقابل حرکت صفحه مقاومت می‌کنند. بنابراین اگر بخواهیم تلاش کنیم که صفحه را به‌ سمت پایین حرکت دهیم، نیرویی در خلاف جهت حرکت آن وجود دارد که در مقابل حرکت صفحه مقاومت می‌کند.به دیفرانسیل dA که باری به اندازه $$dq=\sigma dA$$ را در خود دارد، نیرویی به سمت بالا و برابر با مقدار زیر وارد می‌شود.

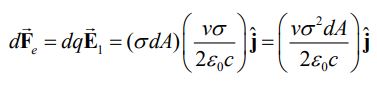
از این رو جهت غلبه بر نیروی کشش، نیرویی به همان اندازه و در خلاف جهت نیروی بالا بایستی به دیفرانسیل مذکور وارد شود. در نتیجه نیروی خارجی وارد به این دیفرانسیل، جهت غلبه بر نیروی ناشی از میدان $$\overrightarrow{E}_1$$ برابر است با:

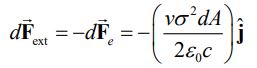
بدیهی است که دیفرانسیل کار انجام شده خارجی برابر با $$dW_{ext} \enspace = \enspace \overrightarrow{F}_{ext}.d\overrightarrow{s}$$ است. از این رو کار انجام شده در واحد سطح، در واحد زمان نیز به شکل زیر بدست می‌آید.

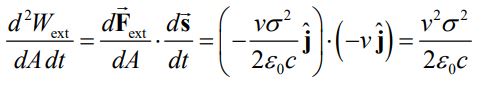
حال به‌نظر شما در مرحله بعد چه اتفاقی رخ خواهد داد؟ زمانی که صفحه‌ای باردار در حال حرکت باشد، در حقیقت با صفحه‌ای از جریان الکتریکی با چگالی $$\overrightarrow{K}= - \enspace\sigma \nu \widehat{j}$$ مواجه‌ایم. با وجود جریان الکتریکی بدیهی است که بر مبنای قانون آمپر، میدان مغناطیسی ایجاد شده برابر است با:

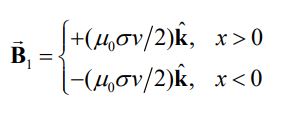
مطابق با شکل زیر در سمت چپ صفحه، میدان ایجاد شده درون‌سو و میدان سمت راست صفحه، برون سو است.

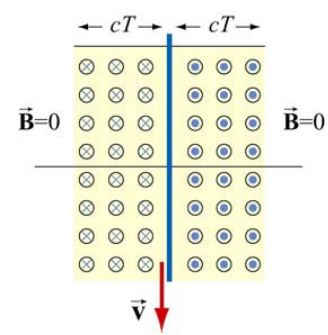
توجه داشته باشید که میدان نشان داده شده در شکل بالا مربوط به فاصله $$|x| \enspace > \enspace cT$$ است. بنابراین در فاصله x| > cT| اندازه میدان $$\overrightarrow{B}$$ برابر با صفر است. هم‌چنین در مبحث امواج الکترومغناطیسی عنوان شد که رابطه زیر بین دامنه‌ میدان‌های مغناطیسی و الکتریکی برقرار است.

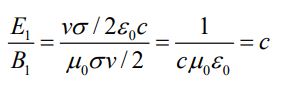
میدان $$\overrightarrow{B}_1$$ که در نتیجه حرکت بار‌های الکتریکی ایجاد می‌شود، عمود بر $$\overrightarrow{E}_1$$ است. هم‌چنین اندازه میدان مغناطیسی ایجاد شده برابر است با:

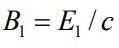
انرژی منتقل شده توسط موج

شار انرژی منتقل شده توسط یک موج الکترومغناطیسی با استفاده از بردار پوئینتینگِ‌ $$\overrightarrow{S}$$ قابل توصیف است. در حقیقت انرژی منتشر شده به سمت راست برابر‌ است با:

فیلم آموزش الکترومغناطیس 1 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

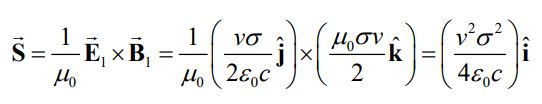
اگر توجه داشته باشید، رابطه بالا نصف مقدار کار انجام شده جهت به حرکت در آوردن صفحه به سمت پایین است. دلیل این امر این است که جهت میدان مغناطیسی در دو سمت صفحه عکس یکدیگر هستند، ولی میدان الکتریکی در دو طرف هم‌جهت است. در حقیقت با جمع زدن موج منتشر شده در جهت راست و چپ، کار کلی مورد نیاز برای حرکت دادن صفحه به سمت پایین بدست می‌آید؛ به بیانی دقیق‌تر انرژی موج الکترومغناطیسی ایجاد شده برابر با کار انجام شده جهت ایجاد خود موج است.

بنابراین می‌توان این سوال را مطرح کرد که انرژی منتقل شده توسط موج الکترومغناطیسی از کدام منبع نشأت می‌گیرد؟ با انجام دادن محاسبات بالا به این نتیجه می‌رسیم که انرژی موجود در موج الکترومغناطیسی همان انرژی اولیه‌ای است که بار‌های الکتریکی را جابجا کرده.

موج الکترومغناطیسی دوره‌ای

با توجه به توصیفات بالا به نظر شما به‌منظور تولید موجی دوره‌ای با فرکانس ω، بار‌های الکتریکی را بایستی به چه شکل به حرکت در آورد؟ جهت ایجاد چنین موجی لازم است صفحه باردار را با سرعت $$\overrightarrow{v}(t) \enspace = \enspace -\nu_0 cos (\omega t) \widehat{j}$$ به نوسان در آورد. میدان مغناطیسی و الکتریکی تولید شده در نتیجه این نوسان برابر است با:

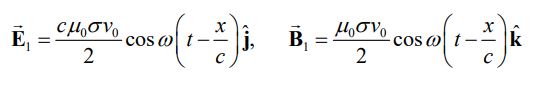
رابطه بالا برای x>0 صادق است. از طرفی میدان تولید شده برای x<0 نیز برابر است با:

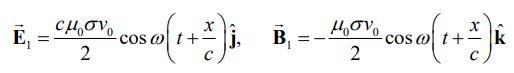
در دو رابطه فوق، دامنه میدان‌ها برابر با مقادیری فرض شده که در بالا، با فرض ثابت بودن سرعت صفحه بدست آمد. اما واقعیت مسئله این است که در این حالت، سرعت صفحه به‌ شکلی سینوسی و با فرکانس زاویه‌ای ω تغییر می‌کند. اما شاید این سوال به ذهن شما خطور کرده باشد که چرا زاویه توابع Cos در روابط بالا به‌صورت t-x/c و t+x/c قرار داده شده است؟

در ابتدا فرض کنید ناظر مفروضی در زمان t، در x>0 قرار دارد. این ناظر، میدان الکتریکی تولید شده در نتیجه نوسان صفحه را اندازه‌گیری می‌کند. بدیهی است که میدان اندازه‌گیری شده نبایستی به ناظر وابسته باشد. زمان مورد نیاز جهت رسیدن اطلاعات از مبدأ به ناظر نیز برابر با x/c است. این جمله به معنای آن است آن‌چه که ناظر مشاهده می‌کند، وابسته به رویدادی است که صفحه حاوی جریان در زمان t-x/c انجام داده. به همین دلیل این عبارت در تابع میدان الکتریکی ظاهر شده. به همین شکل اگر ناظر در x<0 قرار گرفته باشد، آنچه که ناظر در زمان t می‌بیند، در زمان x+c/t رخ داده است. به همین دلیل t+x/c در این حالت برای میدان الکتریکی و مغناطیسی ظاهر شده است.

در روابط بالا دو تابع $$cos \enspace\omega (t-x/c) \enspace = \enspace cos (\omega t-kx)$$ معادل با یکدیگر هستند. در این روابط k=ω/c است و آن را عدد موج می‌نامند. توجه داشته باشید که با استفاده از مفهوم چگالی سطحی می‌توان عبارت $$\overrightarrow{E}_0$$ را از روابط حذف کرد. جهت انجام این کار، صفحه‌ای ساکن را با چگالی بار σ- در مکان x=0 در نظر می‌گیریم. این صفحه باردار فرضی، میدان الکتریکی ناشی از صفحه اولیه را خنثی خواهد کرد، اما روی اغتشاشات وارد شده به میدان الکتریکی تاثیری نخواهد گذاشت؛ دلیل این امر، ساکن بودن صفحه فرضی است.

در واقعیت، امواج الکترومغناطیسی به این شکل ایجاد می‌شوند. در حقیقت در این موارد بار‌های الکتریکی (معمولا الکترون‌ها) در یک جهت شتاب گرفته و بار مخالف به‌صورت ساکن قرار می‌گیرد. در نتیجه یک ناظر فقط موج ایجاد شده را می‌بینید و میدان‌های ایجاد شده به‌طور تنهایی ظاهر نمی‌شوند. در حقیقت در این حالت تنها می‌توان میدان متحرک را مشاهده کرد.

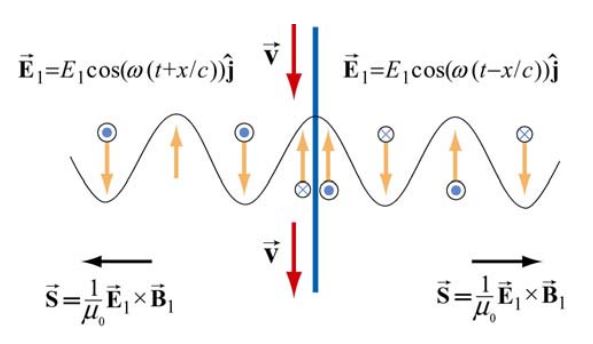
شکل زیر موج ایجاد شده در نتیجه صفحه‌ باردار نوسانی را نشان می‌دهد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک و مهندسی برق آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی برق
• مجموعه آموزش‌های فیزیک
• مجموعه آموزش‌های مهندسی برق
• القای الکترومغناطیسی— از صفر تا صد
• میدان مغناطیسی ناشی از سیم حامل جریان -- از صفر تا صد
• طیف الکترومغناطیسی — به زبان ساده
• مجموعه آموزش‌های نرم‌افزار‌های مهندسی برق و الکترونیک