دیورژانس (Divergence) – به زبان ساده
پیشتر در وبلاگ فرادرس به بررسی مشتق جزئی و توابع چند متغیره پرداخته شد. در این مطلب به صورت دقیق، مفهوم دیورژانس مورد مطالعه قرار میگیرد. دیورژانس و گرادیان از مهمترین مباحث ریاضیات پایه هستند. در آنالیز برداری، دیورژانس یک بردار، برابر با حاصل ضرب داخلی عملگر دِل در آن بردار است. با توجه به آنکه حاصل ضرب داخلی دو بردار، به صورت یک تابع اسکالر است، میتوان نتیجه گرفت که دیورژانس نیز در نهایت به فرم یک تابع اسکالر در میآید.

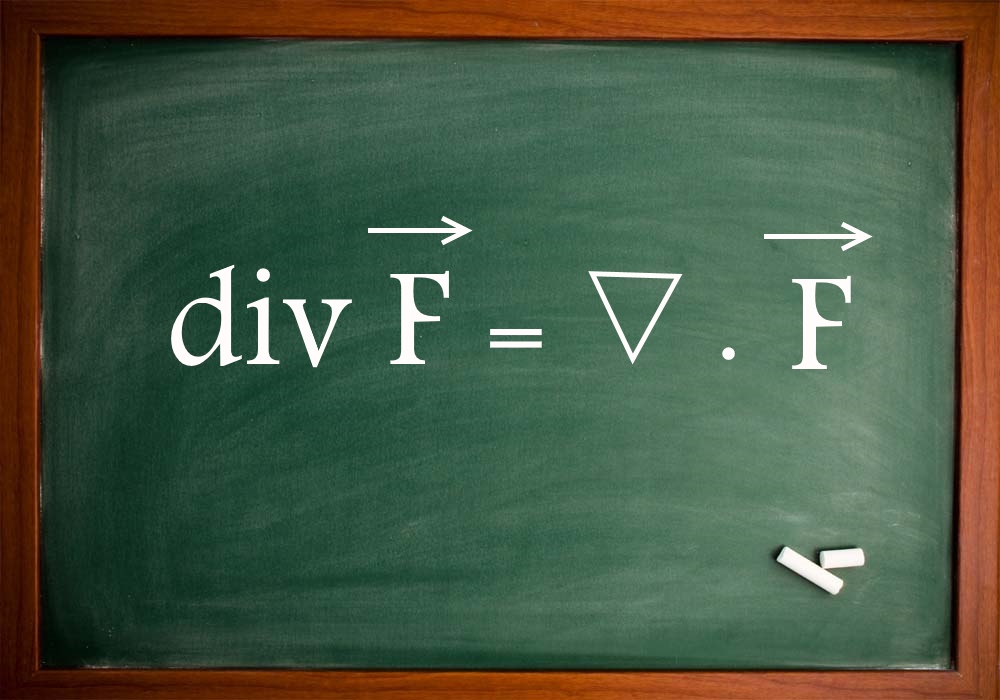
در این مطلب ابتدا رابطه عملگر دیورژانس، تعبیر هندسی و کاربرد آن مورد بررسی قرار میگیرند و در انتهای مطلب، شیوه استفاده از این عملگر در قالب چند مثال نشان داده میشود.
دیورژانس چیست؟
F را یک میدان برداری در فضای سهبعدی به شکل زیر در نظر بگیرید.
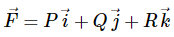
در این رابطه Q ،P و R مولفههای این بردار به ترتیب در راستای y ،x و z هستند. برای تعریف «دیورژانس» (Divergence) ابتدا باید «عملگر دِل» (Del Operator) را معرفی کنیم. این عملگر با نماد ∇ نشان داده میشود و رابطه آن به شکل زیر است.
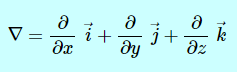
همانطور که در رابطه بالا قابل رویت است، عملگر دِل به صورت یک بردار بیان میشود که مولفههای آن به ترتیب مشتق جزئی در راستای y ،x و z را بیان میکنند.
توجه شود که این عملگر به تنهایی مفهومی را منتقل نمیکند و شیوه اعمال آن بر توابع مختلف باعث ایجاد مفاهیم مختلف میشود. برای مثال ضرب داخلی این عملگر در بردار F مفهوم دیورژانس را تولید میکند که رابطه آن برای بردار F (رابطه ۱) به صورت زیر نمایش داده میشود.
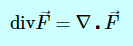
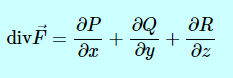
رابطه بالا، دیورژانس بردار F را به صورت سهبعدی نشان میدهد. همچنین میتوان این رابطه را به صورت خلاصه با استفاده از نماد div F = ∇ · F = Px + Qy + Rz نیز بیان کرد. در صورتی که بردار F دوبعدی باشد، این رابطه به صورت زیر در میآید.
div F = ∇ · F = Px + Qy
نکته مهم و قابل توجه در این روابط، این است که دیورژانس یک بردار، درنهایت به صورت یک تابع «اسکالر» (Scalar) خواهد بود.
تفاوت دیورژانس و گرادیان
همانطور که مشاهده شد، شیوه نمایش نمادهای گرادیان و دیورژانس اندکی مشابه یکدیگر هستند و ممکن است بسیاری از دانشجویان این دو مفهوم را با یکدیگر اشتباه بگیرند. بنابراین در این قسمت به بررسی دقیق این دو مفهوم و تفاوت میان آن دو پرداخته میشود.
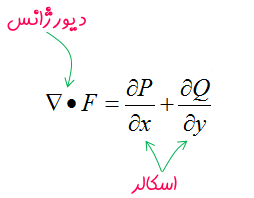
در قسمت قبل اشاره کردیم که دیورژانس، حاصل ضرب نقطهای عملگر دِل در یک بردار است و فرم نهایی آن به شکل یک تابع اسکالر خواهد بود. در حالت دو بعدی، این عملگر به شکل زیر نمایش داده میشود.
اما گرادیان، حاصل اعمال عملگر دِل بر یک تابع اسکالر است که در حالت دو بعدی، به شکل رابطه زیر نمایش داده میشود.
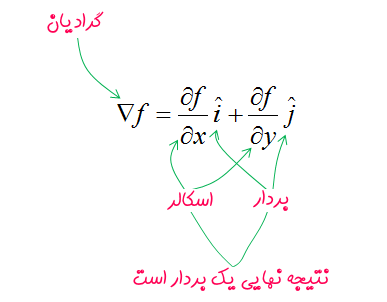
همانطور که در رابطه بالا نشان داده شده است، گرادیان روی یک تابع اسکالر مانند f عمل میکند و در نهایت، خروجی آن به شکل یک بردار است، در حالی که دیورژانس روی یک بردار عمل میکند و خروجی آن به شکل یک اسکالر در میآید.
تعبیر هندسی دیورژانس
فرض کنید F به صورت یک میدان برداری مطابق شکل زیر باشد. همانطور که مشاهده میکنید این میدان به صورت منبسط شونده است و بردارهای آن از مبدأ مختصات در حال دور شدن هستند.
به عنوان یک مثال کاربردی میتوان فرض کرد که بردار F، بردار سرعت آب خروجی از منبعی است که در مبدأ مختصات قرار دارد.
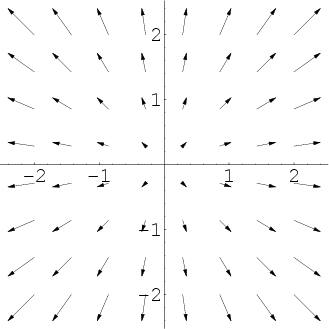
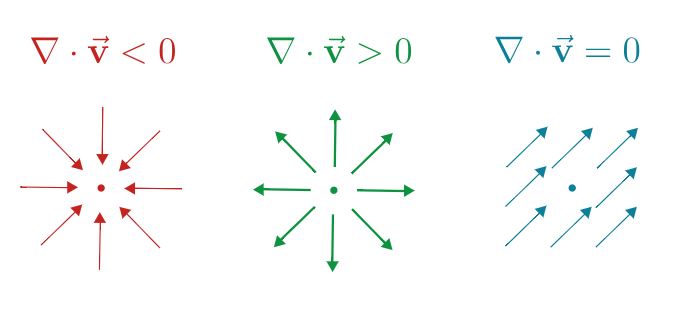
دیورژانس F که به صورت منبسط شونده است برابر با مقداری مثبت خواهد بود. در صورتی که بردارهای نشان داده شده، بردار سرعت آب باشند، دیورژانس F با نماد مثبت نشان میدهد که آب از این منبع خارج شده است (این مورد در مکانیک سیالات اصطلاحا به «ترم چشمه» (Source Term) معروف است).
در مثال دیگری فرض کنید که F به صورت زیر نمایش داده شود. همانطور که مشاهده میکنید این میدان به صورت منقبض شونده است و بردارهای آن به سمت مبدأ مختصات قرار دارند. به عنوان یک مثال کاربردی میتوان F را بردار سرعت آب اطراف منبعی فرض کرد که در مبدأ مختصات قرار دارد.
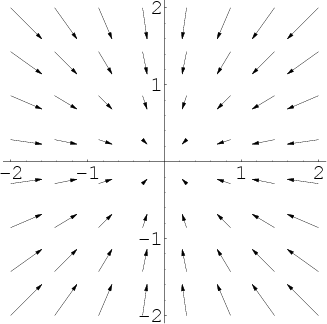
دیورژانس F که در شکل بالا نشان داده شده، برابر با مقداری منفی است. در صورتی که بردارهای نمایش داده شده، بردار سرعت آب اطراف منبع مور نظر باشند، دیورژانس F با نماد منفی نشان میدهد که آب، وارد این منبع شده است (این مورد در مکانیک سیالات اصطلاحا به «ترم چاه» (Sink Term) معروف است).
لوله آبی را در نظر بگیرید، در صورتی که هیچ جرمی به داخل این لوله و یا خارج از آن جریان نداشته باشد، دیورژانس میدان بردارهای سرعت آب در آن برابر با صفر میشود. این موضوع را در مکانیک سیالات، با استفاده از قانون بقای جرم در یک سیستم بدون ترم چشمه و چاه به صورت زیر نشان میدهند.
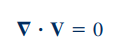
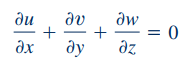
به طور خلاصه علامت دیورژانس بردار V به شکل زیر نمایش داده میشود.
مثالها
در ادامه و در قالب مثالهایی، شیوه محاسبه دیورژانس بردارهای مختلف، مورد ارزیابی قرار داده میشوند.
مثال 1
دیورژانس بردار زیر را محاسبه کنید.
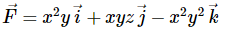
رابطه دیورژانس را برای بردار بالا به شکل زیر مینویسیم. نکته مهم این است که مشتق جزئی ترم سوم این رابطه در راستای z برابر با صفر است.

مثال 2
بردار V را به شکل زیر در نظر بگیرید.
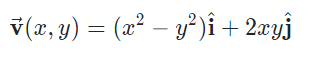
دیورژانس این بردار را محاسبه کنید و مقدار دیورژانس آن را در نقطه (1,2) به دست آورید.
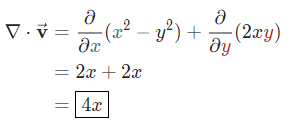
مشتق جزئی هر دو ترم رابطه بالا تنها تابعی از x است و دیورژانس آن به مقدار y بستگی ندارد. در ادامه با جایگذاری مختصات نقطه داده شده در رابطه به دست آمده، مقدار خواسته شده در صورت سوال، به شکل زیر محاسبه میشود.
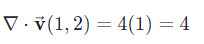
مثال ۳
بردار F را به شکل زیر در نظر بگیرید. دیورژانس این بردار را محاسبه کنید.
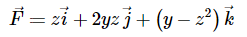
ابتدا رابطه دیورژانس را برای بردار بالا مینویسیم و سپس مشتق جزئی ترمهای مختلف این بردار را به شکل زیر محاسبه میکنیم.
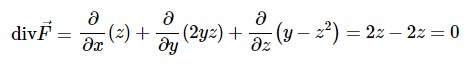
در این مطلب ابتدا به صورت دقیق رابطه عملگر دیورژانس، تعبیر هندسی و کاربرد آن مورد بررسی قرار گرفت و شیوه استفاده از روابط حاکم بر این عملگر در قالب چند مثال نشان داده شد.
در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقهمند هستید، آموزشهای زیر به شما پیشنهاد میشوند:
- مفاهیم مشتق — به زبان ساده
- توابع چند متغیره — به زبان ساده
- گرادیان (Gradient) در ریاضیات — به زبان ساده
^^












با سلام لطفا مفهوم دیورژانس را بیشتر توضیح می دهید مثلا در تابع دوم که دیورژانس آن ۴ شد، مفهوم این عدد ۴ چیست؟
با سلام خدمت شما همراه گرامی؛
دیورژانس یک عملگر ریاضی است که روی میدانهای برداری اعمال میشود و نشان میدهد که آیا میدان برداری در یک نقطه خاص “از” آن نقطه خارج میشود یا “به” آن نقطه وارد میشود یا خیر. اگر میدان برداری را به عنوان جریان یک مایع در نظر بگیرید، دیورژانس مثبت نشان میدهد که جریان از آن نقطه خارج میشود (مانند چشمه) و دیورژانس منفی نشاندهنده ورود جریان به آن نقطه (مانند چاه) است. محاسبه دیورژانس با استفاده از یک فرمول ریاضی است که شامل مشتقات جزئی مولفههای میدان برداری نسبت به مختصات است. در علم فیزیک، دیورژانس میدان برداری میتواند نشاندهنده منبع یا مصرف آن کمیت باشد. برای مثال، دیورژانس میدان سرعت سیال نشاندهنده منبع یا چاه جریان است.
از بازخورد و همراهی شما با مجله فرادرس سپاسگزاریم.
سلام ببخشید برای این مطالب لطفا مرجع بدید من تو هیچ کتاب ریاضی نمیتونم پیداشون کنم خیلی مهمن این روابط
با سلام خدمت شما همراه گرامی؛
در ادامه چند کتاب مرجع دانشگاهی در این زمینه معرفی شده است:
۱- حساب دیفرانسیل و انتگرال توابع چند متغیره – نوشته دکتر علیاکبر لطفیزاده
۲ – ریاضیات مهندسی – جلد 2 (حساب دیفرانسیل و انتگرال) – نوشته دکتر محمدعلی محمدی و همکاران
۳ – مبانی ریاضیات – نوشته دکتر عباس کاظمینژاد
از بازخورد و همراهی شما با مجله فرادرس سپاسگزاریم.
با سلام و سپاس از نحوه آموزش بسيار ساده و روان واقعا جاي همچين آموزش هايي در دوران تحصيل ما دهه شصتي ها خالي بود
بسیار بسیار عالی و کاربردی بود خیلی خیلی ممنونم.
آیا چیزی به اسم قضیه دیورژانس برای گرادیان وجود داره؟
تشکر. ساده ، مفید و کاربردی بود …
خسته نباشید
متشکر
عالی بود ممنون
خسته نباشید خیلی مفید بود
خیلی عالی است و به زبان ساده بیان شده است.
خدا خیرتان بده
خوبه ممنونم
خدایی خدمت میکنید. دمتون گرم عالی بود
بسیار عالی بود متشکرم .خدا خیرتان دهد.
سلام، مرسی عالی بود فقط در تعبیر هندسی از لغت تابع استفاده شده است در صورتی که تابع به ازای هر ورودی حداکثر یک خروجی دارد و خط موازی محور y ها نمیتونه در چند نقطه شکل رو قطع کنه.
سلام
عاشقتونم ?
یاد گرفتم ??
خیلی سپاس
سلام. اصلاحات مورد نظر انجام شد.
از توجه شما سپاسگزاریم.
کارتون درسته
دمتون گرم. ساده و گویا
دمتون گرم. ساده و گویا..
بسیار مفهومی توضیح داده شده و عالی بود
عالی
خیلی عالی