موازنه واریانس و بایاس | به زبان ساده

در نوشتارهای دیگری از مجله فرادرس با مفهوم واریانس و شاخص‌های پراکندگی (Dispersion Measures) و همچنین اریبی یا بایاس (Bias) آشنا شده‌اید. ولی در اینجا قصد داریم بین واریانس و بایاس که هر دو به شیوه و روش خاص خود، میزان خطا را نشان می‌دهند یک تعادل برای مدل‌های آماری برقرار کنیم. در ادبیات مربوط به «یادگیری ماشین» (Machine Learning) چنین امری به موازنه واریانس و بایاس (Bias-Variance Tradeoff) معروف است.

به منظور آشنایی بیشتر با اصطلاحات به کار رفته در این نوشتار، بهتر است مطالب برآوردگر اریب و نااریب — به زبان ساده و امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن تفاوت خطا و مقدار باقیمانده در محاسبات آماری — به زبان ساده و بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی نیز خالی از لطف نیست.

موازنه واریانس و بایاس

در مدل‌های آماری و بخصوص الگوریتم‌های یادگیری ماشین، مسئله موازنه واریانس و بایاس (اریبی) مورد بحث قرار می‌گیرد. در اغلب «مدل‌های پیش‌بین» (Predictive Model)، وجود بایاس کوچک برای پارامترها منجر به واریانس بزرگ برای مدل خواهد شد. البته برعکس این حالت نیز وجود دارد، به این معنی که با کوچک کردن واریانس مدل، با مشکل بزرگ شدن بایاس یا اریبی پارامترها مواجه خواهیم شد.

مسئله اصلی آن است که در یک مدل مناسب، هم بایاس و هم واریانس باید حداقل ممکن باشند. ولی متاسفانه، کمینه‌سازی (Minimization) هر دو این شاخص‌ها به شکل توام، امکان‌پذیر نیست. چنین وضعیتی را «تناقض واریانس-اریبی» (Bias-Variance Dilemma) می‌نامند. در ادامه هر یک از خطاها را معرفی کرده و نحوه ایجاد تعادل واریانس و اریبی را بازگو خواهیم کرد.

خطای حاصل از بایاس و واریانس

یک مدل آماری را در نظر بگیرید. قرار است پارامترهای این مدل توسط نمونه تصادفی برآورد شوند. به منظور اندازه‌گیری خطای مدل، مجموعه داده‌های مربوط به نمونه تصادفی را به دو بخش تقسیم می‌کنیم. قسمت اول به منظور برآورد پارامترهای مدل مورد استفاده قرار می‌گیرد، به همین علت چنین مقادیری را «داده‌های آموزشی» (Training Set) نامیده و به واسطه آن‌ها، مدل را ایجاد می‌کنیم.

قسمت یا بخش دوم از نمونه تصادفی برای مشخص کردن خطای مدل به کار می‌رود زیرا قرار است این مدل به منظور پیش‌بینی مقادیر دیگری که در نمونه تصادفی وجود نداشته‌اند، به کار رود. به این ترتیب از دسته یا بخش دوم نمونه تصادفی برای محاسبه اختلاف مقادیر واقعی و نتایج حاصل برازش مدل استفاده می‌کنیم. متاسفانه از آنجایی که مدل از قبل از وجود این داده‌ها اطلاع نداشته و نتوانسته خود را برحسب آن‌ها وفق دهد، امکان کنترل این خطا وجود ندارد. برای این دسته از مقادیر نمونه از اصطلاح «داده‌های آزمایشی» (Test Set) استفاده می‌کنیم.

براساس این دو بخش از نمونه تصادفی، علاقمند به ایجاد مدلی هستیم که در هر دو حالت یعنی هنگام آموزش (Train) و آزمایش (Test)، خطای کمی داشته باشد. خطای حاصل از به کارگیری مدل روی داده‌های آموزشی، بایاس مدل گفته شده و از طرفی خطای مدل روی داده‌های آزمایشی، واریانس مدل در نظر گرفته می‌شود.

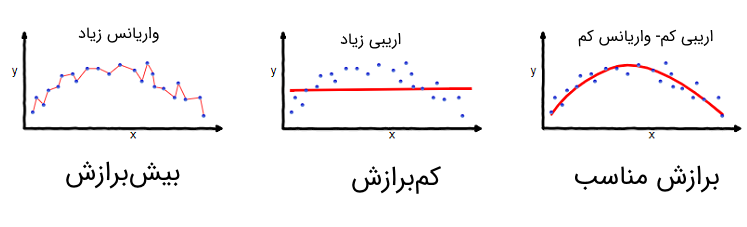
• خطای بایاس: وجود فرضیه‌های مختلف روی مدل و الگوریتم یادگیری منجر به ایجاد خطای اریبی می‌شود. بزرگ بودن اریبی می‌تواند الگوریتم یا مدل آماری را از کشف روابط یبن ویژگی‌ها (Features) و متغیر پاسخ (Target Variable) باز دارد. اغلب بزرگ بودن خطای اریبی، منجر به «کم‌برازش» (Underfitting) می‌شود.
• خطای واریانس: حساسیت زیاد مدل با تغییرات کوچک روی داده‌های آموزشی، نشانگر وجود واریانس زیاد است. این امر نشانگر آن است که اگر مدل آموزش داده شده را روی داده‌های آزمایشی به کارگیریم، نتایج حاصل با داده‌های واقعی فاصله زیادی خواهند داشت. متاسفانه افزایش واریانس در این حالت منجر به مدل‌بندی مقادیر نوفه (Noise) شده و به جای پیش‌بینی صحیح، دچار پیچیدگی و مشکل «بیش‌برازش» (Overfitting) می‌شود.

مشکلات استفاده از مدل‌های بایاس و با واریانس بزرگ

در علم داده (Data Science)، موازنه واریانس و بایاس (اریبی) به یک مسئله اصلی در «یادگیری نظارت شده» (Supervised Machine Learning) تبدیل شده است. در حالت ایده آل، مدلی را مناسب در نظر می‌گیریم که نه تنها در داده‌های آموزش دارای عملکرد مناسب باشد، بلکه به خوبی روی مجموعه مقادیر آزمایشی نیز تعمیم داده شود. متأسفانه انجام هر دو کار به طور هم زمان غیر ممکن است. روش‌های یادگیری با واریانس بالا، ممکن است بتوانند مدل مناسبی روی داده‌های آموزشی خود ایجاد کنند، اما هنگامی که چنین مدلی به منظور پیش‌بینی مقادیر براساس داده‌های آزمایشی مورد استفاده قرار می‌گیرد در ارائه مقادیر مناسب و با خطای کم برای متغیر پاسخ ناتوان خواهد بود. در مقابل، الگوریتم‌هایی که دارای بایاس زیاد هستند، معمولاً مدل‌های ساده‌تر و با پارامترهای کمتری ایجاد می‌کنند که مشکل بیش‌بردازش نداشته ولی متاسفانه از کم‌برازش رنج می‌برند.

مدل‌های با واریانس بزرگ (مثلا رگرسیون چند جمله‌ای هم‌مرتبه با تعداد مشاهدات)، که معمولاً پیچیده‌تر هستند، این امکان را می‌دهد تا داده‌های آموزشی به خوبی برازش شوند. با این وجود، ممکن است مشاهدات برازش شده دارای خطا یا نوفه باشند که متاسفانه مدل تحت تاثیر آن‌ها، برآوردها را با دقت انجام داده است. به این ترتیب پیش‌بینی‌ آن‌ها باعث افزودن پیچیدگی در مدل شده است. در حالیکه این امر از طرفی دقت برآوردها را هم برای داده‌های آزمایشی کمتر می‌کند. در مقابل، مدل‌هایی که دارای اریبی بزرگی هستند، نسبتاً ساده بوده (مثل مدل رگرسیون دو جمله‌ای یا حتی خطی) اما ممکن است واریانس کوچکتری را براساس مجموعه داده‌های آزمایشی ایجاد کنند.

موازنه واریانس و بایاس با تجزیه مربعات خطا

فرض کنید مجموعه آموزشی شامل نقطه‌هایی مانند $$x_1,x_2, \ldots,x_n$$ به عنوان مقادیر متغیر مستقل باشد و برای هر یک از آن ها نیز مقدار متغیر پاسخ به صورت $$y_i$$ ثبت شده است.

فیلم آموزش تخمین خطای طبقه بندی یا کلاسیفایر در داده کاوی در فرادرس

کلیک کنید

مدل مورد نظر برای رابطه بین متغیرهای مستقل و پاسخ به صورت $$y=f(x)+\varepsilon$$ است که در آن $$\varepsilon$$ یک عبارت تولید خطا با میانگین صفر و واریانس $$\sigma^2$$ است.

هدف ایجاد یک مدل به منظور برآورد مقادیر $$\widehat{y}$$‌ یا $$\widehat{f}(x;D)$$ است بطوری که این برآورد، بتواند مقدار واقعی تابع $$f(x)$$ را با کمترین خطا، تخمین بزند. این کار به واسطه یک الگوریتم یادگیری (Learning Algorithm) روی یک بخش از نمونه تصادفی به نام مجموعه داده آموزشی (Training Dataset) صورت می‌گیرد که از این به بعد آن را با شکل $$D=\{(x_1,y_1), \; ,\ldots,(x_n,y_n)\}$$ نشان می‌دهیم.

همچنین در نظر بگیرید که تابع زیان برای اندازه‌گیری میزان خطای چنین مدلی، میانگین مربعات خطا است. به این ترتیب مدل ایجاد شده باید دارای کمترین میانگین مربعات خطا نسبت به مدل‌های دیگر باشد. بر این اساس $$(y-\widehat{f}(x;D))^2$$ باید هم برای $$x_1,x_2,\ldots,x_n$$ و هم برای نقاط خارج از آن که البته در نمونه تصادفی و مجموعه داده‌های آزمایشی (Test Dataset) قرار دارند،‌ کمینه باشد.

از آنجایی که مدل با یک عبارت یا جمله خطا ($$\varepsilon$$) معرفی شده، انتظار نداریم که مدل برازش شده با خطای صفر، عمل برآورد را انجام دهد ولی به وسیله روش‌های ریاضی و آماری، سعی در پیدا کردن مدلی با کمترین میانگین مربعات خطا هستیم.

اگر مجموعه داده آموزشی ($$D$$) را مبنای میانگین‌گیری در نظر بگیریم، هدف پیدا کردن تابعی مثل $$\widehat{f}$$ است که طرف راست رابطه زیر را کمینه سازد.

$$\large { \displaystyle \operatorname {E} _{D}{\Big [}{\big (}y - {\hat {f}}(x;D){\big )}^{2}{\Big ] } = {\Big (} \operatorname {Bias} _{D}{\big [}{\hat {f}}(x;D){\big ]}{\Big )}^{2} + \operatorname {Var} _{D}{\big [}{ \hat {f}}(x;D){\big ]} + \sigma ^{2}}$$

توجه دارید که در این رابطه، اریبی یا بایاس، براساس داده‌های آموزشی به صورت زیر است.

$$\large { \displaystyle \operatorname {Bias} _{D}{\big [}{\hat {f}}(x;D){ \big ]} = \operatorname {E} _{D}{\big [}{\hat {f}}(x;D){ \big ]} - f(x)}$$

همچنین واریانس مدل برآورد شده به کمک مشاهدات آموزشی از طریق رابطه زیر محاسبه می‌شود.

$$\large {\displaystyle \operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){\big ]} = \operatorname {E} _{D}[{\hat {f}}(x;D)^{2}]-\operatorname {E} _{D}[{\hat {f}}(x;D)]^{2}}$$

از آنجایی که ممکن است نمونه‌های مختلف به عنوان مجموعه داده آموزشی $${\displaystyle D=\{(x_{1},y_{1})\dots ,(x_{n},y_{n})\}}$$ به کار رود، گزاره‌های زیر را برای نمونه‌های حاصل از جامعه آماری $$P(x,y)$$ می‌توان بیان کرد.

• مربع میزان بایاس یا اریبی یک الگوریتم یادگیری وابسته به میزان ساده‌سازی شرایط مدل دارد. برای مثال اگر از یک مدل خطی (Linear Model) برای یک تابع $$f(x)$$ که غیرخطی (Non-Linear) است، استفاده کنیم دچار خطای بایاس براساس فرض خطی بودن مدل خواهیم شد.
• واریانس الگوریتم یادگیری بیانگر آن است که مقدار برآورد $$\widehat{f}(x)$$ در الگوریتم، چقدر حول میانگین آن نوسان دارد.
• ثابت بودن واریانس عبارت خطا نیز یکی از شرط‌های مهم در مدل رگرسیونی در نظر گرفته می‌شود. در غیر اینصورت ممکن است، مدل دچار بیش‌برازش یا کم‌برازش شود.

از آنجایی که همه منابع خطا (مربع اریبی، واریانس مدل یا واریانس عبارت خطا) مثبت یا حداقل نامنفی هستند، می‌توان یک کران پایین برای خطای مدل روی داده‌های آزمایشی در نظر گرفت.

هر چه مدل $$\widehat{f}(x)$$ پیچیده‌تر باشد، نقاط بیشتری از داده‌های آموزشی را پوشش می‌دهد و بایاس و اریبی نیز کم خواهد بود. در حالیکه یک مدل پیچیده، باعث بوجود آمدن خطای زیاد برای برازش داده‌های جدید خواهد شد در نتیجه واریانس مدل را برای چنین داده‌هایی، زیاد می‌کند.

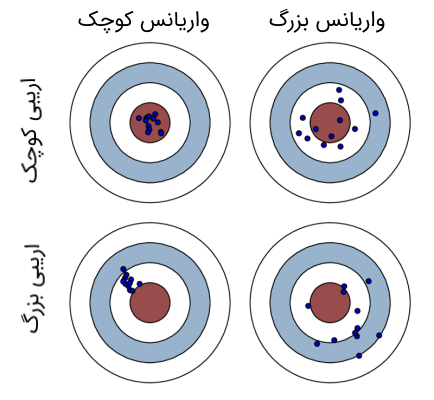
تفکیک خطا به واریانس و بایاس

به کمک تکنیکی که در ادامه معرفی می‌کنیم، خطای مدل را به واریانس و بایاس یا اریبی تجزیه می‌کنیم. به منظور سادگی در فرمول‌های بعدی به نکات زیر توجه کنید.

$$\large f = f(x) , \;\; \widehat{f} = \widehat{f}(x ; D)$$

براساس تعریفی که از امید ریاضی و واریانس یک متغیر تصادفی مثل $$X$$‌ داریم، می‌توانیم رابطه زیر را بنویسیم:

$$\large { \displaystyle \operatorname {Var} [X] = \operatorname {E} [X^{2}] - { \Big (} \operatorname {E} [X]{\Big )}^{2}}$$

با تغییر دادن و جابجا کردن دو طرف تساوی به رابطه زیر خواهیم رسید.

$$\large { \displaystyle \operatorname {E} [X^{2}] = \operatorname {Var} [X] + {\Big (}\operatorname {E} [X]{\Big )}^{2}}$$

از آنجای که $$f$$ «قابل تعیین» (Deterministic) و همچنین از مجموعه مشاهدات یا $$D$$ مستقل است، داریم:

$$\large {\displaystyle \operatorname {E} [f] = f}$$

با فرض $$y = f +\varepsilon$$ و $$\operatorname{E}[\varepsilon]=0$$ خواهیم داشت:

$$\large {\displaystyle \operatorname {E} [y] = \operatorname {E} [f + \varepsilon ] = \operatorname {E} [f] = f}$$

از طرفی واریانس عبارت خطا برابر است با $$\operatorname{Var} [ \varepsilon] = \sigma^2$$ است. پس

$$\large { \displaystyle \operatorname {Var} [y] = \operatorname {E} [ (y - \operatorname {E} [y])^{2}] = \operatorname {E} [(y-f)^{2}] = \operatorname {E} [( f + \varepsilon -f)^{2}] }$$

$$= \large \operatorname {E} [ \varepsilon ^{2}] = \operatorname {Var} [ \varepsilon ] + {\Big (} \operatorname {E} [ \varepsilon ]{\Big )}^{2} = \sigma ^{2}$$

از آنجایی که $$\varepsilon$$ و $$\widehat{f}$$ مستقل هستند، تساوی‌های زیر برقرار خواهند بود.

$$\large {\displaystyle {\begin{aligned}\operatorname {E} {\big [}(y - {\hat {f}})^{2}{\big ]}& = \operatorname {E} {\big [}(f + \varepsilon -{\hat {f}})^{2}{\big ]}\\[5pt]& = \operatorname {E} {\big [}(f+\varepsilon -{\hat {f}} + \operatorname {E} [{\hat {f}}]-\operatorname {E} [{\hat {f}}])^{2}{\big ]}\\[5pt]&=\operatorname {E} {\big [}(f-\operatorname {E} [{\hat {f}}])^{2}{\big ]} + \operatorname {E} [\varepsilon ^{2}]+\operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})^{2}{\big ]}\\ \large & + 2 \operatorname {E} {\big [}(f-\operatorname {E} [{\hat {f}}])\varepsilon {\big ]} + 2\operatorname {E} {\big [}\varepsilon (\operatorname {E} [{\hat {f}}]-{\hat {f}}){\big ]} +\operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})(f-\operatorname {E} [{\hat {f}}]){\big ]}\\[5pt]& = (f -\operatorname {E} [{\hat {f}}])^{2} + \operatorname {E} [\varepsilon ^{2}] + \operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}] - {\hat {f}})^{2}{\big ]} \\ \large & + 2 (f - \operatorname {E} [{\hat {f}}])\operatorname {E} [\varepsilon ] + 2\operatorname {E} [\varepsilon ]\operatorname {E} {\big [}\operatorname {E} [{\hat {f}}]-{\hat {f}}{\big ]} + 2\operatorname {E} {\big [}\operatorname {E} [{\hat {f}}] - {\hat {f}}{\big ]}(f-\operatorname {E} [{\hat {f}}])\\[5pt]&=(f-\operatorname {E} [{\hat {f}}])^{2} + \operatorname {E} [\varepsilon ^{2}] + \operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}] - {\hat {f}})^{2}{\big ]}\\[5pt]& = (f-\operatorname {E} [{\hat {f}}])^{2}+\operatorname {Var} [y] + \operatorname {Var} {\big [}{\hat {f}}{\big ]}\\[5pt]&=\operatorname {Bias} [{\hat {f}}]^{2 } + \operatorname {Var} [y] + \operatorname {Var} {\big [}{\hat {f}}{\big ]}\\[5pt]& = \operatorname {Bias} [{\hat {f}}]^{2} + \sigma ^{2} + \operatorname {Var} {\big [}{\hat {f}}{\big ]} \end{aligned}}}$$

در نهایت، تابع زیان MSE (میانگین مربعات خطا) یا لگاریتم درستنمایی منفی به کمک محاسبه امید ریاضی و طبق رابطه زیر حاصل می‌شود.

$$\large { \displaystyle { \text{MSE}} = \operatorname {E} _{x}{\bigg \{} \operatorname {Bias} _{D}[{\hat {f}}(x;D)]^{2} + \operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){ \big ]}{\bigg \}} + \sigma ^{2}}$$

رویکردهای موازنه واریانس و بایاس یا اریبی

استفاده از روش‌های «کاهش بُعد» (Dimensionality Reduction) و «انتخاب ویژگی» (Feature Selection) می‌توانند واریانس را به کمک ساده‌سازی مدل انجام دهند. از طرفی افزایش داده‌های آموزشی باعث کاهش واریانس خواهد شد.

افزایش تعداد متغیرهای پیش‌گو (Predictors)، باعث کاهش بایاس (اریبی) می‌شود ولی این امر به قیمت افزایش واریانس خواهد بود. الگوریتم‌های یادگیری، معمولا از یک پارامتر تنظیم کننده برای موازنه واریانس و بایاس استفاده می‌کنند. الگوریتم‌هایی که در ادامه معرفی شده‌اند، احتیاج به قاعده‌سازی دارند.

• در «مدل خطی» (Linear Model) و «مدل خطی تعمیم یافته» (Generalize Linear Model) می‌توان به کمک قاعده‌سازی (Regularized)، موازنه بین واریانس و بایاس را برقرار کرد، در غیر این صورت با کاهش واریانس، بایاس افزایش خواهد یافت.
• در «شبکه‌های عصبی مصنوعی» (Artificial Neural Networks)، واریانس و بایاس با افزایش تعداد گره‌های مخفی (Hidden Nodes) افزایش می‌یابند. به همین علت باید قاعده‌سازی در آن‌ها به کار گرفته می‌شود.
• مدل‌های $$k$$-نزدیکترین همسایه (k-nearest neighbor models) با افزایش مقدار $$k$$،‌ میزان واریانس کاهش یافته ولی بایاس افزایش خواهد یافت.
• در تکنیک درخت تصمیم (Decision Tree)، عمق درخت، میزان واریانس را مشخص می‌کند. با استفاده از روش «هرس کردن» (Pruning)، مقدار واریانس کنترل می‌شود.

علاوه بر قاعده‌سازی، استفاده از «مدل‌های ترکیبی» (Mixture Model) و «یادگیری جمعی» (Ensemble Learning) نیز می‌تواند موازنه واریانس و بایاس را برقرار سازند. برای مثال «روش‌های تقویتی» (Boosting) به شکلی عمل کرده که مدل‌های ضعیف (با بایاس زیاد) را با یکدیگر ترکیب کرده بطوری که میزان بایاس مدل نهایی نسبت به مدل‌های اولیه کمتر است. در مقابل در تکنیک «گروه‌بندی» (Bagging)،‌ الگوریتم‌های یادگیری قوی (با واریانس زیاد) با یکدیگر ترکیب شده تا نتیجه، مدلی با واریانس کاهش‌یافته نسبت به مدل‌های اصلی پدید آید.

البته روش‌های دیگر مانند «اعتبارسنجی متقابل» (Cross Validation) برای تعیین میزان پیچیدگی مدل‌های آماری به کار گرفته شده و باعث موازنه واریانس و بایاس یا اریبی می‌شوند

کاربرد در رگرسیون

تجزیه میزان خطای کل به واریانس و بایاس،‌ همچنین بهره‌گیری از کمینه‌سازی آن‌ها در مدل رگرسیونی، ایده اصلی در روش‌های رگرسیون با قاعده‌سازی (Regularization) نظیر «رگرسیون لاسو» (Lasso Regression) و «رگرسیون ستیغی» (Ridge Regression) است. روش‌های قاعده‌سازی، بایاس را وارد روش حل و برآورد پارامترهای مدل کرده و به این ترتیب واریانس مدل را نسبت به روش‌های رگرسیون عادی (Ordinary Least Squares) یا OLS کاهش می‌دهند. هر چند روش‌های مبتنی بر OLS، برآوردگرهای نااریب برای پارامترهای رگرسیونی ایجاد می‌کنند ولی وجود واریانس کوچکتر در مدل‌های رگرسیونی با قاعده‌، مفید‌تر بوده و مقادیر برآورد شده توسط آن‌ها، دارای خطای کمتری هستند.

کاربرد در رده‌بندی

تجزیه واریانس و بایاس در ابتدا، برای رگرسیون حداقل مربعات (OLS) به کار گرفته شد. ولی این تکنیک برای طبقه‌بندی (Classification) تحت تابع زیان صفر و یک (Zero-One Loss function) یا تابع خطای طبقه‌بندی (Misclassification Rate)، می‌تواند تجزیه مشابهی را ایجاد کرد. از طرف دیگر ، اگر بتوان مسئله طبقه‌بندی را به عنوان یک مدل رده‌بندی احتمالی (Probabilistic Classification) بیان کرد، امکان بهره‌گیری از میانگین خطای مربعات پیش‌بینی شده از مدل احتمالاتی و تجزیه آن به بایاس و واریانس وجود دارد.

خلاصه و جمع‌بندی

در این نوشتار به بررسی مسئله تناقض موازنه واریانس و بایاس پرداختیم. در بسیاری از روش‌های یادگیری ماشین، این مشکل و تناقض وجود دارد و امکان کاهش هر دو این منابع خطا وجود ندارد. به این ترتیب با استفاده از تکنیک‌هایی مانند جریمه کردن مدل، مثلا در «رگرسیون لاسو» (Lasso Regression) یا «رگرسیون ستیغی» (Ridge Regression) موازنه واریانس و بایاس برقرار می‌شود و مدلی بدون کم‌برازش یا بیش‌برازش بدست می‌آید.

اگر مطلب بالا برای شما مفید بوده است، نوشتارهای دیگر مجله فرادرس و همچنین آموزش‌های ویدیویی که در زیر معرفی شده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش های مدل سازی، برازش و تخمین
• آموزش برنامه نویسی متلب برای علوم و مهندسی
• مجموعه آموزش‌های داده کاوی و یادگیری ماشین
• مهم‌ترین الگوریتم‌های یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده 
• رگرسیون ستیغی (Ridge Regression) در پایتون — راهنمای کاربردی