معادله شرودینگر — به زبان ساده

در این مقاله سعی داریم به طور خیلی ساده مروری بر پیدایش فیزیک کوانتومی داشته و در نهایت به معادله‌ای تحت عنوان معادله شرودینگر برسیم که توصیف‌ کننده امواج وابسته به ذرات میکروسکوپی است. با ما در ادامه مقاله همراه باشید.

پیدایش کلمه کوانتیده

می‌توان گفت سرآغاز فیزیک کوانتوم به اوایل قرن بیستم میلادی، یعنی زمانی که دانشمند و فیزیکدان مشهور آلمانی ماکس پلانک (Max Planck) سعی در توجیه تابش جسم سیاه داشت، بر‌ می‌گردد. آن زمان پلانک از واژه نا‌آشنای کوانتیزه (کوانتیده) برای بیان مقدار انرژی تابش شده از جسم سیاه استفاده کرد. اساساً مفهوم کوانتیده، در مقابل مفهوم پیوسته، برای متغیرهایی که تنها مقادیر مشخصی را می‌توانند اختیار کنند، نظیر تابش الکترومغناطیسی به کار می‌رود.

اجازه دهید با یک مثال جالب این مفهوم را برای همیشه در ذهن شما ثبت کنیم. فرض کنید لوله‌ای که درون آن پر از اسمارتیز است در دست دارید. در اینجا تعداد اسمارتیزها عددی مشخص بوده و به صورت گسسته (۱،۲،۳ و ...) شمارش می‌شود. شما می‌توانید لوله را به قسمت‌های مختلفی تقسیم کنید یا لوله‌های دیگری را نیز اختیار کنید. در این صورت تعداد اسمارتیزها ممکن است که کم یا اضافه شود، با این حال، ما برای شمارش تعداد اسمارتیزها بازهم از مقداری گسسته (کوانتیده) استفاده می‌کنیم. نظرتان چیست که لوله را یک پرتو نور و اسمارتیزها را فوتون‌ها در نظر بگیریم؟!

پلانک هنگام کار روی تابش جسم سیاه و نارسایی‌هایی آن که به «فاجعه فرابنفش» (Ultraviolet Catastrophe) معروف است، پی برد که انرژی تابش الکترومغناطیسی نمی‌تواند مقادیر پیوسته‌ای داشته باشد. طبق قوانین الکترومغناطیس کلاسیک، تعداد مُدهایی (حالت‌هایی) که یک موج الکترومغناطیسی می‌تواند در کاواک ۳ بعدی ارتعاش کند، با مربع فرکانس متناسب است. درواقع مطابق با قانون ریلی-جینز (Rayleigh-Jeans)، مقدار توان نیز با مربع فرکانس برابر بوده و این امر بدین معنی است که در فرکانس‌های خیلی بالا (بی‌نهایت) مقدار توان نیز باید بی‌نهایت شود. دلیل نام‌گذاری «فاجعه فرانبفش» روی این نارسایی همین امر است. چرا که در فرکانس‌های ناحیه فرانبفش و بالاتر تجربه و روابط ریاضی دو چیز متفاوت را نتیجه می‌دادند.

فیلم آموزش فیزیک مدرن با رویکرد حل مساله در فرادرس

کلیک کنید

پلانک گفت که انرژی تابش الکترومغناطیسی از قوانین کلاسیکی پیروی نمی‌کند، بلکه این انرژی در بسته‌هایی متناسب با فرکانس و به طور گسسته (کوانتیده) تغییر می‌کند. انرژی تابش الکترومغناطیسی مطابق با رابطه زیر منتشر می‌شود:

$$E=hf$$

گاهی اوقات رابطه فوق را به صورت نیز $$E=ℏω$$ می‌نویسند. در رابطه فوق $$h$$ ثابت پلانک با مقدار عددی $$6.626×10^{-34}j.s$$ است. مقدار $$ℏ$$ نیز برابر با $$ℏ=\frac{h}{2\pi}$$ در نظر گرفته می‌شود. این رابطه بیانگر این است که در فرکانس‌های بی‌نهایت مقدار تابش به صفر می‌رسد. رفتار کوانتوم به دلیل وجود h که مقداری غیر صفر دارد، متفاوت با رفتار کلاسیکی است.

بسته‌های کوچک نور

اگر شما برای مدتی نوری را روی سطح یک فلز بتابانید، مشاهده می‌کنید که سطح آن گرم شده و نتیجه می‌گیرید که نور به سطح فلز، انرژی منتقل می‌کند. شاید استدلال کنید که اگر برای مدتی طولانی نور را روی سطح جسمی بتابانید، انرژی لازم برای جدا شدن الکترون از مدارش رفته رفته فراهم شده و در نهایت الکترون رها و باعث ایجاد گرما در سطح جسم می‌شود. از همین استدلال احتمالاً نتیجه بگیرید که حتی اگر با نوری خیلی ضعیف اما برای مدت خیلی طولانی این کار را انجام دهید، الکترون انرژی لازم برای رها شدن از سطح جسم را به دست می‌آورد!

اما بر خلاف تصور و استدلال اولیه، نتایج آزمایش فیزیکدانان بیانگر مطلب دیگری است. در واقع ممکن است که تابش نوری مشخص بر سطح یک فلز باعث جدایی الکترون و در نتیجه ایجاد گرما در سطح آن شود، اما اگر همان نور را برای فلز با عناصر دیگری به کار ببریم این اتفاق رخ ندهد. با تکرار آزمایش با نوری پر انرژی‌تر (نوری با فرکانس بالاتر) مشاهده شد که الکترون انرژی لازم برای رهایی از مدارش را دریافت می‌کند. در واقع در اینجا، مدت زمان و حتی شدت نور تابیده شده ملاک نیست، بلکه انرژی لازم برای جدایی الکترون، فقط تابعی از رنگ (فرکانس) نور تابیده شده است.

مسئله فوق که به پدیده «فوتوالکتریک» (Photoelectric) معروف است، به دست آلبرت اینشتین حل و فرمول‌بندی شد. او دیدگاه و تئوری کوانتیده بودن ماکس پلانک را در خصوص نور، اعمال و بیان کرد که نور جریان پیوسته‌ای از انرژی نیست. بلکه نور متشکل از تعداد زیادی بسته‌های کوچک انرژی بوده که مقدار انرژیش تابعی از طول موج یا فرکانس $$(f=c/\lambda)$$ است.

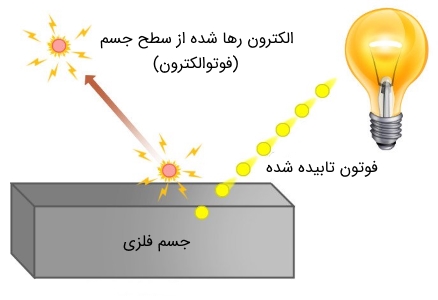
بنابراین مطابق با تعبیر فوق، تنها نور (شامل بسته‌های انرژی که اسمشان را فوتون می‌گذاریم) با انرژی کافی توانایی جدا کردن الکترون از سطح جسمی که به آن می‌تابد را فارغ از مدت زمان و شدت تابش، دارد. مطابق با معادله پلانک $$(E=hf)$$ واضح است که چرا تغییر رنگ (در واقع تغیر فرکانس) نور باعث جدا شدن الکترون از سطح جسم می‌شود. اینشتین نشان داد که انرژی الکترون آزاد شده از سطح جسم برابر با مقدار زیر است:

$$E=hf-\phi$$

در رابطه فوق، $$\phi$$ به تابع کار جسم معروف بوده و بیانگر حداقل میزان انرژی لازم برای جدا شدن الکترون از سطح جسم است.

معادله شرودینگر

حال که با مقدماتی از چگونگی پیدایش فیزیک کوانتوم آشنا شدید، به سراغ معادله‌ای می‌رویم که رفتار موجی ذرات را توصیف می‌کند. در مقاله «دوگانگی موج و ذره — به زبان ساده» دیدیم که دوبروی به هر ذره با تکانه $$p$$، موجی با طولی موج $$\lambda$$ نسبت داد. موج مذکور به موج مادی یا «امواج ذرات» (Matter Waves) معروف است. اروین شرودینگر معادله‌ای را بر اساس قضیه طول موج دوبروی توسعه داد که موج وابسته به ذرات و چگونگی تغییر حالت سیستم‌های کوانتومی را توصیف می‌کند. برای رسیدن به معادله مذکور روند زیر را طی می‌کنیم.

با پاسخ معادله موج استاندارد زیر شروع می‌کنیم:

$$\begin{equation*} A(x,t) = A_{0}e^{i(kx-\omega t)} \end{equation*}$$
(۱)

فیلم آموزش فیزیک مدرن با رویکرد حل مساله در فرادرس

کلیک کنید

از معادله فوق مشخص است که موج به مختصه مکانی ($$x$$) و زمانی ($$t$$) وابسته است. معادله (۱) در واقع پاسخ معادله موج زیر است. در ادامه قصد بررسی این معادله موج را داریم. می‌خواهیم نشان دهیم، معادله موج (۲) برای توصیف امواج وابسته به ذرات (منظور امواجی که حرکت یک الکترون را شرح می‌دهند) مناسب نیست.

$$\begin{equation*} \frac{\partial^2 A}{\partial x^2} = \frac{1}{c^2}\frac{\partial^2 A}{\partial t^2} \end{equation*}$$
(۲)

معادله فوق بیان می‌کند که اگر دو مرتبه از معادله توصیف موج $$A$$ (معادله ۱) نسبت به متغیر $$x$$ مشتق گرفته شود، نتیجه حاصل با مشتق مرتبه دوم موج $$A$$ نسبت به زمان $$t$$ با ضریب  $$\frac{1}{c^2}$$ متناسب است.

برای اینکه درستی عبارت فوق (معادله ۲) را تحقیق کنیم، از معادله موج $$A$$ نسبت به مختصه مکانی $$x$$ دوبار مشتق می‌گیریم:

$$\frac{\partial^{2} A}{\partial x^2} = -k^{2}A_{0}e^{ikx}e^{-i\omega t}=-k^2A$$
(۳)

حال از معادله موج $$A$$ نسبت به متغیر زمانی $$t$$ دوبار مشتق می‌گیریم:

$$\frac{\partial^{2} A}{\partial t^2} = -\omega^{2}A_{0}e^{ikx}e^{-i\omega t}=-\omega^2A$$
(۴)

طبق معادله (2) و محاسبات انجام شده داریم:

$$-k^{2}A = \frac{-\omega^2A}{c^2}$$
(5)

که با ساده کردن $$A$$ از طرفین معادله خواهیم داشت:

$$\begin{equation*} \omega = ck \end{equation*}$$
(۶)

حال دو رابطه مهم فیزیک کوانتوم، یعنی فرمول انرژی ($$E=hf$$) و طول موج دوبروی ($$\lambda=\frac{h}{p}$$) را در نظر بگیرید. این روابط را به فرم زیر بازنویسی می‌کنیم. یادآور می‌شویم که $$k=\frac{2\pi}{\lambda}$$ ، $$ℏ=\frac{h}{2\pi}$$ و $$\omega=2\pi f$$ هستند.

$$\begin{equation*} E=\hbar\omega \end{equation*}$$
$$\begin{equation*} p = \hbar k \end{equation*}$$
(7)

از روابط (۷) و (۶) نتیجه می‌شود:

$$\frac{E}{\hbar} = c \frac{p}{\hbar}$$
$$E=pc$$
(8)

برای ذرات یا اجسام غیر نسبیتی رابطه (۸) ناکارآمد بوده و رابطه بین انرژی و تکانه به فرم آشنای کلاسیکی زیر است:

$$\begin{equation*} E=\frac{p^2}{2m} \end{equation*}$$
(9)

به نظر می‌رسد که مطابق با روابط فوق، معادله موج (۲) برای توصیف امواج وابسته به ذرات ناکارآمد باشد. چرا که معادله (۲) رابطه بین ω و $$k$$ را به فرم خطی $$\begin{equation*} \omega = ck \end{equation*}$$ نتیجه داد. شاید یک راه حل برای رفع این مشکل این باشد که رابطه بین ω و $$k$$ به شکل $$ω∝k^2$$ تغییر کند. برای این کار معادله موجی به فرم زیر را امتحان می‌کنیم:

$$\frac{\partial^2 \psi}{\partial x^2} = \alpha\frac{\partial \psi}{\partial t}$$
(10)

در معادله فوق $$A$$ را با نماد ψ که بیانگر نمایش موجی در مکانیک کوانتوم است (یک قرار داد)، جایگزین می‌کنیم. توجه شود که ψ موجی همانند رابطه (۱) است. با انجام محاسبات خواهیم داشت:

$$\frac{\partial^{2} \psi}{\partial x^2} = -k^{2}\psi_{0}e^{ikx}e^{- \ i\omega t}=-k^2\psi$$
$$\frac{\partial \psi}{\partial t} = -i\omega\psi$$
(11)

که در نتیجه :

$$-k^2=-i\alpha\omega \rightarrow \omega=\frac{k^2}{i\alpha}$$
(12)

با جایگذاری $$\omega$$ در رابطه $$\begin{equation*} E=\hbar\omega \end{equation*}$$ خواهیم داشت:

$$E=\hbar\frac{k^2}{i\alpha}$$
(13)

با تعریف مقدار ثابت α به فرم زیر:

$$\alpha=\frac{-2mi}{\hbar}$$
(14)

معادله (13) به فرم زیر نتیجه می‌شود:

$$E=\frac{\hbar^2k^2}{2m}=\frac{p^2}{2m}$$
(15)

حال به نظر می‌رسد که معادله موجی در دست داریم که جوابی صحیح برای توصیف انرژی ماده را نتیجه‌ می‌دهد. اجازه دهید یک بار دیگر معادله (10) را با جایگذاری مقدار ثابت α بازنویسی کنیم:

$$\frac{\partial^2 \psi}{\partial x^2} = \frac{-2mi}{\hbar}\frac{\partial \psi}{\partial t}$$
(16)

با انجام کمی عملیات ریاضی می‌توان آن را به فرم زیر نوشت:

$$i\hbar\frac{\partial \psi}{\partial t} = \frac{\hbar^2}{2m}\frac{\partial^2 \psi}{\partial x^2}$$
(17)

تقریباً به معادله مد نظرمان برای توصیف موجی ذرات رسیدیم. با جایگذاری معادلات (۱۱) در معادله (۱۷)، انرژی ذره به شکل زیر به دست می‌آید:

$$E\psi=\left(\frac{p^2}{2m}\right)\psi$$
(18)

به طور کلی یک ذره می‌تواند از محیط اطراف انرژی بگیرد. برای مثال تحت تاثیر یک پتانسیل باشد. بنابراین برای کامل شدن معادله (18)، تغییر جزئی زیر را وارد معادله می‌کنیم:

$$E\psi=\left(\frac{p^2}{2m} + V\right)\psi$$
(19)

رابطه فوق بیان می‌کند که معادله موج باید به فرم زیر در آید.

$$i\hbar\frac{\partial \psi}{\partial t} = \left(- \ \frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V\right)\psi$$
(20)

معادله فوق به معادله شرودینگر یک بعدی وابسته به زمان معروف است. با در نظر گرفتن مختصه مکانی $$y$$ و $$z$$ یعنی حالت کلی‌تر ۳ بعدی، مشتق مرتبه دوم مکانی $$x$$ با عبارت لاپلاس جایگزین و معادله به شکل کلی زیر در می‌آید:

$$i\hbar\frac{\partial \psi}{\partial t} = \left(\frac{\hbar^2}{2m}\triangledown^{2}+V\right)\psi$$
(21)

معادله فوق در اواخر سال 1925 میلادی توسط اروین شرودینگر (Erwin Schrödinger) فرمول‌بندی شد. به طور کل این معادله چگونگی تغییر حالت سیستم‌های کوانتومی را شرح می‌دهد.

وابستگی زمانی معادله شرودینگر

در قسمت قبل با معادلاتی برای توصیف موجی ذرات نظیر الکترون آشنا شدیم که پتانسیل متناظر با آن‌ها وابستگی زمانی نداشت و به طور ناگهانی با گذشت زمان تغییر نمی‌کرد. اما در اغلب مواقع شرایط اینگونه ساده نیست. از این‌ رو برای حل این دست از مسائل از روش جداسازی متغیرها در معادله شرودینگر استفاده می‌کنیم.

در قدم اول فرض می‌کنیم که معادله (۱) را بتوان به دو تابع $$u$$ و $$T$$ تفکیک کرد. تابع $$u$$ فقط تابعی از مختصه مکانی $$x$$ و تابع $$T$$ فقط تابعی از مختصه زمانی $$t$$ است.

$$\psi(x,t)=u(x)T(t)$$
(22)

فیلم آموزش مکانیک کوانتومی 1 – جامع و با نکات کاربردی در فرادرس

کلیک کنید

با جایگذاری رابطه فوق در معادله شرودینگر (20) داریم:

$$i\hbar\frac{\partial uT}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 uT}{\partial x^2} + VuT$$
(23)

با کمی انجام محاسبات ریاضی ساده، معادله فوق به شکل زیر در می‌آید:

$$i\hbar\frac{1}{T}\frac{\partial T}{\partial t} = -\frac{1}{u}\frac{\hbar^2}{2m}\frac{\partial^2 u}{\partial x^2} + V$$
(24)

سمت راست معادله فوق فقط تابعی از مختصه مکانی و سمت چپ فقط تابعی از مختصه زمانی است. حال فرض کنید که زمان مقداری تغییر کند. از آنجا که سمت راست معادله، مستقل از زمان است، تغییر در زمان باعث برهم خوردن تساوی در معادله می‌شود. برای رفع این مشکل دو طرف معادله را برابر با مقدار ثابت $$E$$ قرار می‌دهیم. در این صورت خواهیم داشت:

$$\begin{equation*} i\hbar\frac{\partial T}{\partial t} =ET \end{equation*}$$
(25)

$$\begin{equation*} -\frac{\hbar^2}{2m}\frac{\partial^2 u}{\partial x^2} + Vu = Eu \end{equation*}$$
(2۶)

بنابراین برای مسائلی که تابع پتانسیل آن‌ها مستقل از زمان است، می‌توان معادله (۲۵) را نادیده گرفت و از رابطه (26) که به رابطه شرودینگر مستقل از زمان معروف است، استفاده کرد. حال برای اینکه صحت مطالب گفته شده را بسنجیم، برای یک ذره آزاد یعنی ذره‌ای که تحت تاثیر هیچ پتانسیلی نیست ($$V=0$$) معادله (26) را حل می‌کنیم. جواب معادله تابعی به فرم زیر است:

$$u=Ae^{ikx}$$
(27)

که در آن $$k$$ مقدار زیر را دارد:

$$k=\sqrt{\frac{2mE}{\hbar^2}}$$
(28)

معادله (۲۷) در واقع قسمت مکانی معادله موج رابطه (۱) ($$\psi = Ae^{i(kx-\omega t)}$$) است. در اینجا $$E$$ مقدار انرژی کل سیستم بوده و اگر ما مقدار آن را بدانیم خیلی راحت می‌توانیم با معادله موج کار کنیم. برای سیستمی با $$E$$ ثابت، مولفه $$T$$ تاثیری بر تابع موج ψ (معادله ۲۲) نداشته و در نتیجه مربع اندازه تابع موج ($$|\psi |^2$$) برابر با مربع اندازه مولفه u ($$|u |^2$$) تابع موج است. در واقع داریم:

$$\int^{\infty}_{-\infty} |u|^2dx=1$$
(29)

حل مسائل با معادله شرودینگر

در این قسمت از این نوشتار حل مسائل و شرایط مختلف را با استفاده از معادله شرودینگر بررسی می‌کنیم. از معادله شرودینگر داریم:

$$\large -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \Psi(x)}{\partial x^2}+V(x)\Psi(x)=E\Psi(x)$$

فیلم آموزش اپتیک کوانتومی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

که سمت چپ معادله بالا در حقیقت هامیلتونی تابع موج است که برابر با انرژی جنبشی و پتانسیل ذره است. برای یک ذره آزاد که هیچ شرایط محدود کننده‌ای روی آن اثر نمی‌گذارد می‌توان گفت پتانسیل برابر با صفر است. در نتیجه در حالت اول معادله شرودینگر را برای یک ذره آزاد با پتانسیل صفر مورد بررسی قرار می‌دهیم.

حل معادله شرودینگر برای یک ذره آزاد

برای یک ذره آزاد پتانسیل در همه جا برابر با صفر است و معادله شرودینگر به صورت زیر در می‌آید:

$$\large -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \Psi(x)}{\partial x^2}=E\Psi(x)$$

اگر ثابت‌ها را به سمت راست تساوی انتقال دهیم داریم:

$$\large\frac{\partial^{2} \Psi}{\partial x^2}=-\frac{2mE}{\hbar^2}\Psi$$

معادله بالا می‌گوید که مشتق دوم تابع موج برابر با خود تابع موج است. این ویژگی به ما این امکان را نشان می‌دهد که ممکن است ثابت این معادله توان دوم باشد که آن را با $$k$$ نمایش می‌دهیم و داریم:

$$\large \frac{\partial^{2} \Psi}{\partial x^2}=-k^2\Psi$$

که در معادله بالا $$k$$ برابر با $$\frac{\sqrt{2mE}}{\hbar}$$ است. این معادله اینک شبیه معادله نوسانگر است که جوابی به صورت زیر برای آن به دست آوردیم:

$$\large \Psi=Ae^{ikx}+Be^{-ikx}$$

که هر دو حالت $$(ik)^2$$ و $$(-ik)^2$$ برابر با $$-k^2$$ است. در این حالت اگر تابع موج علاوه بر مکان یعنی $$x$$ به زمان یعنی $$t$$ بستگی داشته باشد جواب تابع موج به صورت زیر در می‌آید:

$$\Psi=Ae^{ikx} e^{(-i\frac{Et}{\hbar})}+Be^{-ikx} e^{(-i\frac{Et}{\hbar})}$$

با توجه به رابطه $$E$$ و $$k$$ شکل نهایی تابع موج به صورت زیر به دست می‌آید:

$$\large \Psi(x, t)=A e^{i k\left(x-\frac{\hbar k}{2 m} t\right)}+B e^{-i k\left(x+\frac{\hbar k}{2 m} t\right)}$$

حل معادله شرودینگر در یک جعبه با پتانسیل صفر

در این حالت یک جعبه به طول $$L$$ را در نظر بگیرید که داخل جعبه پتانسیل صفر است و ذره در جعبه به عقب و جلو می‌رود. همچنین فرض کنید جابه‌جایی ذره در یک بُعد و تنها در راستای $$x$$ اتفاق می‌افتد. هیچ نیروی دیگری بر روی ذره داخل جعبه اعمال نمی‌شود و پتانسیل در خارج جعبه بی نهایت است.

فیلم آموزش مکانیک کوانتومی 1 – مرور و حل تمرین در فرادرس

کلیک کنید

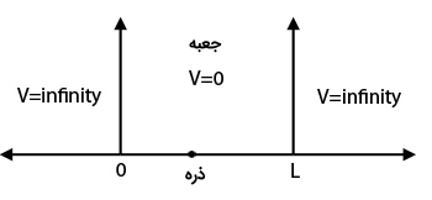
چون وابستگی به زمان وجود ندارد پس تابع موج و جواب تابع موج به صورت زیر است:

$$\large \frac{d^{2} \psi}{d x^{2}}+\frac{8 \pi^{2} m E \psi}{h^{2}}=0$$

$$\large \psi(x)=A \cos \left(\sqrt{\frac{8 \pi^{2} m E}{h^{2}}} x\right)+B \sin \left(\sqrt{\frac{8 \pi^{2} m E}{h^{2}}} x\right)$$

حال باید شرایط مرزی را بر جواب اعمال کنیم. با توجه به شرایط داده شده در مسئله در $$x<0$$ و $$x>L$$ نمی‌توانیم جوابی را برای تابع موج پیدا کنیم زیرا در این بازه‌ها انرژی پتانسیل بی‌نهایت است و ذره در صورت وجود در این نواحی باید انرژی بی‌نهایت داشته باشد. همچنین به دلیل پیوستگی تابع موج، این تابع در $$x=0$$ نیز صفر است و داریم:

$$\large 0=A \cos 0+B \sin 0=A$$

و بدن ترتیب تابع موج به صورت زیر به دست می‌آید:

$$\large \psi=B \sin \left(\sqrt{\frac{8 \pi^{2} m E}{h^{2}}} x\right)$$

همچنین در $$x=L$$ نیز تابع موج برابر با صفر است و داریم:

$$\large 0=B \sin \left(\sqrt{\frac{8 \pi^{2} m E}{h^{2}}} L\right)$$

در این حالت اگر B نیز صفر باشد، بدین معنی است که کل تابع موج صفر است و ذره در جعبه وجود ندارد. در حالی که ما می‌دانیم ذره در جایی در جعبه وجود دارد پس ضریب تابع سینوس را برابر با صفر در نظر می‌گیریم و داریم:

$$\large 0=\sin(\sqrt{\frac{8 \pi^{2} m E}{h^{2}}} L)$$

و با توجه به ویژگی‌های توابع مثلثاتی داریم:

$$\large \sqrt{\frac{8 \pi^{2} m E}{h^{2}}} L=0, \pi, 2\pi,3\pi, \dots$$

به بیان دیگر باید گفت:

$$\large \sqrt{\frac{8 \pi^{2} m E}{h^{2}}} L=n\pi$$

که n اعداد صحیح مثبت است و با ساده سازی داریم:

$$\large E_{n}=\frac{n^{2} h^{2}}{8 m L^{2}}$$

در رابطه بالا $$n=0,1,2,3\dots$$ است و اعداد کوانتیده سطوح انرژی هستند. برای به دست آوردن مقدار B در این تابع موج باید چگالی احتمال یافتن ذره در جعبه در زمان t را بنویسیم و داریم:

$$\large \int_{0}^{L}|\Psi(x)|^{2} d x=\int_{0}^{L}|\psi(x)|^{2} d x$$

با توجه به اینکه مطمئن هستیم ذره در جایی داخل جعبه هست، پس چگالی احتمال تابع موج ذره برابر با ۱ است و داریم:

$$\large \int_{0}^{L} B^{2} \sin ^{2}\left(\sqrt{\frac{8 \pi^{2} m E}{h^{2}}} x\right) d x=1$$

با توجه به اینکه می‌دانیم $$\large \int \sin ^{2}(a x) d x=-\frac{1}{2 a} \sin (a x) \cos (a x)+\frac{x}{2}$$ در نتیجه داریم:

$$\large B=\sqrt{\frac{2}{L}}$$

تونل زنی کوانتومی

مثال آخر از مباحث مربوط به معادله شرودینگر، مربوط به تونل زنی کوانتومی است. بر این اساس و بر اساس فیزیک کلاسیک یک ذره برای عبور از یک کوه پتانسیل با مقدار $$V$$ نیاز دارد مقدار انرژی برابر یا بیشتر از ارتفاع این کوه داشته باشد تا از آن عبور کند. در مکانیک کوانتوم گاهی یک ذره با داشتن انرژی کمتر از پتانسیل در طرف دیگر قله پتانسیل دیده می‌شود که به این پدیده تونل زنی کوانتومی می‌گویند.

فیلم آموزش فیزیک مدرن با رویکرد حل مساله در فرادرس

کلیک کنید

ولی این پدیده چگونه رخ می‌دهد. شکل زیر را در نظر بگیرید که مقدار پتانسیل در هر سه ناحیه داده شده است و داریم:

$$\large U(x)=\left\{\begin{array}{ll} 0, & \text { when } x<0 \\ U_{0}, & \text { when } 0 \leq x \leq L \\ 0, & \text { when } x>L \end{array}\right.$$

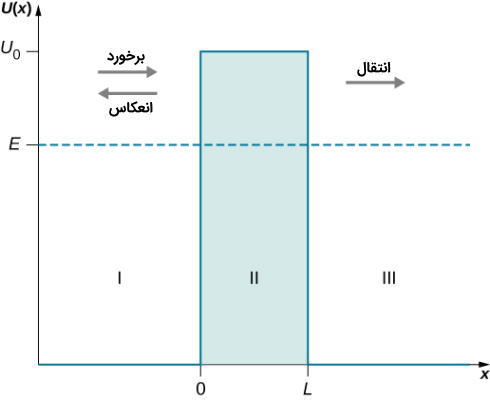
هنگامی که ارتفاع و عرض سد پتانسیل یعنی $$L$$ و $$U_0$$ متناهی باشند، قسمتی از بسته موج برخورد کرده با سد به داخل سد پتانسیل نفوذ کرده و بعد از مدتی در طرف دیگر این سد دیده می‌شود. اینکه چه مقدار از موج برخورد کرده با سد تونل زنی کنند و در سمت دیگر سد دیده شوند به ارتفاع سد یا $$U_0$$، انرژی موج و عرض سد پتانسیل یا $$L$$ بستگی دارد. بدین ترتیب برای سه ناحیه می‌توانیم معادله شرودینگر را بنویسیم. همچنین فرض می‌کنیم که انرژی موج ورودی یعنی $$E$$ کوچکتر از ارتفاع سد یعنی $$U_0$$ است و از این طریق می‌توانیم پدیده جذاب تونل زنی کوانتومی را بررسی کنیم. برای ناحیه I که بین $$-\infty$$ است، معادله شرودینگر با توجه به این که پتانسیل در این منطقه صفر است شکل زیر را دارد:

$$\large -\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi_{I}(x)}{d x^{2}}=E \psi_{I}(x)$$

در ناحیه II که بین $$0$$ پتانسیل وجود دارد و برابر با $$U_0$$ است و بدین ترتیب برای معادله شرودینگر داریم:

$$\large -\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi_{I I}(x)}{d x^{2}}+U_{0} \psi_{I I}(x)=E \psi_{I I}(x)$$

در ناحیه III که بین $$L$$ است و پتانسیل صفر است، معادله شرودینگر مجدداً به صورت زیر است:

$$\large -\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi_{I I I}(x)}{d x^{2}}=E \psi_{I I I}(x)$$

با توجه به شرط پیوستگی تابع موج بین نقطه صفر و $$L$$ باید دو شرط زیر برقرار باشد و داریم:

$$\psi_I(0) = \psi_{II}(0)$$

$$\psi_{II}(L) = \psi_{III}(L)$$

همچنین مشتق تابع موج نیز در مرزها باید در دو ناحیه با یکدیگر برابر باشد و در نتیجه داریم:

$$\large \left.\dfrac{d\psi_I(x)}{dx}\right|_{x = 0} = \left.\dfrac{d\psi_{II}(x)}{dx}\right|_{x = 0}$$

$$\large \left.\dfrac{d\psi_{II}(x)}{dx}\right|_{x = L} = \left.\dfrac{d\psi_{III}(x)}{dx}\right|_{x = L}$$

با توجه به صفر بودن پتانسیل در منطقه I و III می‌توانیم تابع موج را در این دو ناحیه به صورت زیر بنویسیم و داریم:

$$\large \begin{array}{c} \psi_{I}(x)=A e^{+i k x}+B e^{-i k x} \\ \psi_{I I I}(x)=F e^{+i k x}+G e^{-i k x} \end{array}$$

در ناحیه I دو موج وجود دارد، یکی موجی که برخورد می‌کند و دیگری موجی که منعکس می‌شود. پس هر دو ضریب A و B غیرصفر هستند. در ناحیه III فقط یک موج منتقل شده وجود دارد و در نتیجه ثابت G که شامل بخش موهومی موج است برابر با صفر است.

بنابراین دامنه موج برخوردی به سد پتانسیل برابر با $$A^2$$، دامنه موج منعکس شده برابر با $$B^2$$ و دامنه موج منتقل شده برابر با $$F^2$$ است. برای محاسبه احتمال پدیده تونل زنی کوانتومی باید نسبت بین موج منتقل شده به موج برخوردی به سد پتانسیل را به دست آوریم و داریم:

$$\large \begin{aligned} T(L, E) &=\frac{\left|\psi_{t r a}(x)\right|^{2}}{\left|\psi_{i n}(x)\right|^{2}} \\ &=\frac{|F|^{2}}{|A|^{2}} \\ &=\left|\frac{F}{A}\right|^{2} \end{aligned}$$

که $$L$$ عرض سد پتانسیل است و $$E$$ انرژی کل ذره است. همچنین این احتمال به ارتفاع سد یعنی $$U_0$$ نیز بستگی دارد. برای ناحیه II می‌توان تابع موج را به صورت زیر نوشت:

$$\large \frac{d^2\psi_{II}(x)}{dx^2} = \beta^2 \psi_{II}(x)$$

که $$\beta^2$$ مثبت است زیرا $$U_0>E$$ و $$\beta$$ یک عدد حقیقی است و داریم:

$$\large \beta^2 = \frac{2m}{\hbar^2}(U_0 - E)$$

حل مربوط به ناحیه II برخلاف نواحی دیگر نوسانی نیست و یک تضعیف تدریجی را نشان می‌دهد و بدین ترتیب داریم:

$$\large \psi_{II}(x) = Ce^{-\beta x} + De^{+\beta x}$$

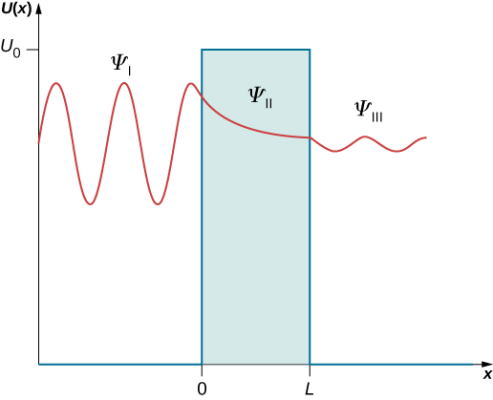
با استفاده از شرایط مرزی و برای $$x=0$$ داریم:

$$\large A+B= C+D$$

و با استفاده از شرایط مرزی برای $$x=L$$ داریم:

$$\large Ce^{-\beta L} + De^{+\beta L} = Fe^{+ik L}$$

همچنین با استفاده از پیوستگی مشتق تابع در $$x=0$$ و $$x=L$$ داریم:

$$\large -ik(A - B) = \beta(D - C)$$
$$\large \beta (De^{+\beta L} - Ce^{-\beta L}) = +ikFe^{+ikL}$$

بدین ترتیب چهار معادله و پنج مجهول داریم. با این حال اگر هر چهار معادله را بر A تقسیم کنیم تا بتوانیم نسبت $$\frac{F}{A}$$ را پیدا کنیم، تعداد مجهول‌های معادله چهار تا می‌شود. با کمی محاسبات می‌توانیم نسبت $$\frac{F}{A}$$ را به صورت زیر به دست آوریم:

$$\large \frac{F}{A} = \frac{e^{-ikL}}{cosh \, (\beta L) + i (\gamma /2) \, sinh \, (\beta L)}$$

که در این معادله $$\gamma \equiv \beta/k - k/\beta$$ است. با قرار دادن این مقدار در رابطه $$T(L,E)$$ و محاسبه احتمال تونل زنی داریم:

$$\large T(L,E) = \left(\frac{F}{A}\right)^*\frac{F}{A} = \frac{e^{+ikL}}{\cosh \, (\beta L) - i (\gamma /2) \, \sinh \, (\beta L)} \cdot \frac{e^{-ikL}}{\cosh \, (\beta L) + i (\gamma /2) \, \sinh \, (\beta L)}$$

یا

$$\large T(L,E) = \frac{1}{\cosh^2 \, (\beta L) + (\gamma /2)^2 \, \sinh^2 \, (\beta L)}$$

که $$(\frac{\gamma}{2})^{2}$$ برابر است با:

$$\large \left(\frac{\gamma}{2}\right)^2 = \frac{1}{4}\left( \frac{1 - E/U_0}{E/U_0} + \frac{E/U_0}{1 - E/U_0} - 2\right)$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• مجموعه آموزش‌های ریاضیات
• آموزش فیزیک مدرن با رویکرد حل مساله
• آموزش مکانیک کوانتومی ۱
• چاه پتانسیل — به زبان ساده
• هسته اتم یا نوکلید (Nuclide) — به زبان ساده
• فوتون در فیزیک — به زبان ساده
• درهم تنیدگی کوانتومی -- به زبان ساده

^^