محیط مثلث قائم الزاویه – به زبان ساده + حل مثال های متنوع

محیط مثلث قائم الزاویه از جمع کردن اندازه وتر و ساق‌های آن به دست می‌آید. در حالت کلی محیط مثلث حاصل جمع سه ضلع آن است. با این وجود مثلث‌های قائم الزاویه دارای ویژگی‌های منحصر به فردی هستند که امکان محاسبه محیط آن‌ها را با روش‌های مختلف فراهم می‌کند. در این مطلب از مجله فرادرس نحوه محاسبه محیط مثلث قائم الزاویه را به زبان ساده و به همراه حل چندین مثال متنوع آموزش می‌دهیم.

محیط مثلث قائم الزاویه چیست؟

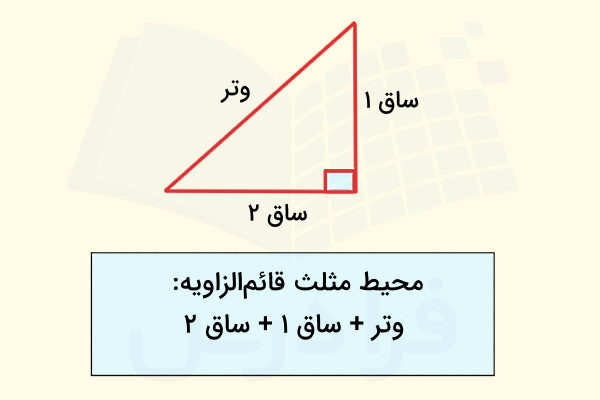
محیط مثلث قائم الزاویه مجموع اندازه وتر و ساق‌های آن است و فرمول آن به شکل زیر محاسبه می‌شود:

اندازه ساق ۲ + اندازه ساق ۱ + اندازه وتر = محیط مثلث قائم‌الزاویه

برای مثال، مثلث قائم الزاویه (الف ب پ) را به شکل زیر در نظر بگیرید:

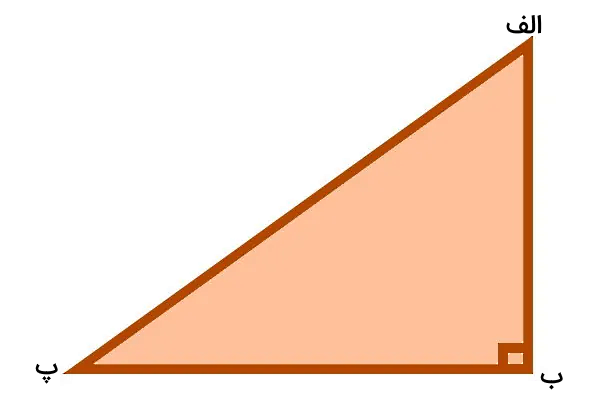
قلم خود را بر روی گوشه (الف) قرار دهید و یک پاره‌خط از این گوشه به گوشه (ب) بکشید. پاره‌خط دوم را از گوشه (ب) تا گوشه (پ) و پاره خط سوم را از گوشه (پ) به گوشه (الف) رسم کنید:

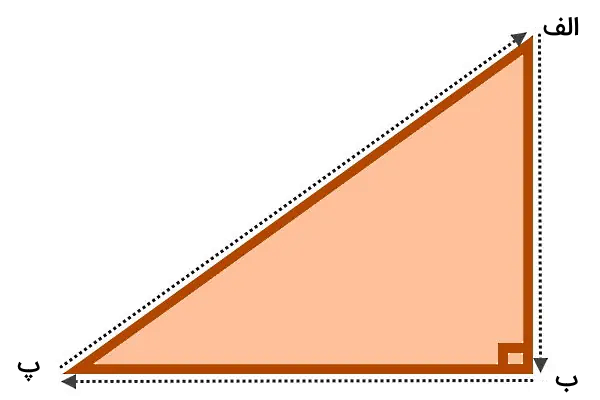
در طی این مراحل شما در حال رسم کردن محیط مثلث قائم الزاویه بودید. طول هر پاره خط را با خط‌کش اندازه‌گیری کنید. با جمع اندازه‌های به دست آمده، محیط مثلث به دست می‌آید. به این ترتیب، می‌توانیم بگوییم که:

طول (الف ب) + طول (ب پ) + طول (پ الف) = محیط مثلث

در مثلث (الف ب پ)، ضلع‌های (الف ب) و (ب پ)، ساق‌های مثلث قائم الزاویه و ضلع (الف پ) وتر مثلث قائم الزاویه بودند. در نتیجه، رابطه بالا به شکل زیر نوشته می‌شود:

وتر + ساق دوم + ساق اول = محیط مثلث قائم الزاویه

عبارت جبری رابطه بالا را در بخش‌ بعدی معرفی می‌کنیم.

فرمول محیط مثلث قائم الزاویه چیست؟

مثلث قائم الزاویه ABC را در نظر بگیرید. اندازه ساق‌های این مثلث با حروف a و b و اندازه وتر آن با حرف c نمایش داده شده است:

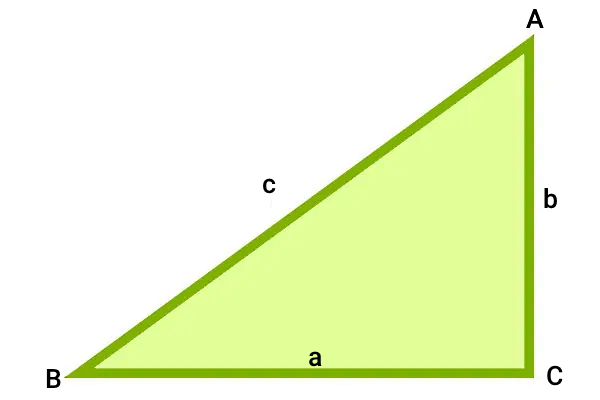
در اکثر کتاب‌ها و منابع آموزشی، نامگذاری وتر و ساق‌های مثلث قائم الزاویه به همین صورت انجام می‌شود. محیط مثلث بالا برابر است با:

ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث

به عبارت دیگر، رابطه بالا برای مثلث قائم الزاویه به صورت زیر نوشته می‌شود:

وتر + ساق دوم + ساق اول = محیط مثلث قائم الزاویه

به جای وتر و ساق‌ها، حروف انگلیسی مرتبط با اندازه آن‌ها را در رابطه بالا قرار می‌دهیم:

a + b + c = محیط مثلث قائم الزاویه

در نتیجه، فرمول محیط مثلث قائم الزاویه برابر است با:

$$P = a + b + c$$

• P: محیط
• a: اندازه یکی از ساق‌ها
• b: اندازه ساق دیگر
• c: اندازه وتر

مثال ۱

طول ضلع‌های مثلث قائم الزاویه زیر با خط‌کش اندازه‌گیری شده و در اندازه هر ضلع در کنار آن نشان داده شده است. محیط این مثلث را حساب کنید.

پاسخ

محیط مثلث قائم الزاویه، جمع اندازه وتر و ساق‌های آن است:

وتر + ساق دوم + ساق اول = محیط مثلث قائم الزاویه

5 + 4 + 3 = محیط مثلث قائم الزاویه

5 + 7 = محیط مثلث قائم الزاویه

12 = محیط مثلث قائم الزاویه

در نتیجه، محیط مثلث برابر ۱۲ است.

مثال ۲

اندازه وتر و ساق‌های یک مثلث قائم الزاویه به ترتیب برابر ۱۳، ۱۲ و ۵ سانتی‌متر است. محیط این مثلث را به دست بیاورید.

پاسخ

به منظور محاسبه محیط مثلث قائم الزاویه از فرمول زیر استفاده می‌کنیم:

$$P = a + b + c$$

• P: محیط
• a: اندازه یکی از ساق‌ها برابر ۱۲
• b: اندازه ساق دیگر برابر ۵
• c: اندازه وتر برابر ۱۳

اندازه وتر و ساق‌ها را درون فرمول بالا قرار می‌دهیم و آن را حل می‌کنیم:

$$P = 12 + 5 + 13$$

$$P = 30$$

در نتیجه، محیط مثلث برابر ۳۰ است.

مثلث قائم الزاویه چیست؟

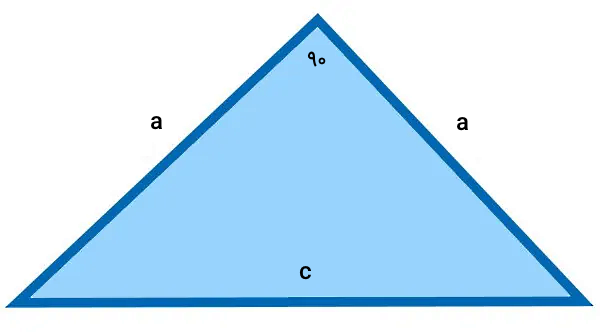
مثلث قائم الزاویه، یک شکل هندسی با ۳ ضلع و ۳ گوشه است که یکی از گوشه‌های آن، زاویه راست یا قائمه (زاویه ۹۰ درجه) دارد. به ضلع‌های تشکیل دهنده زاویه راست، «ساق» و به ضلع مقابل زاویه راست، «وتر» می‌گویند. تصویر زیر، یک مثلث قائم الزاویه را نمایش می‌دهد:

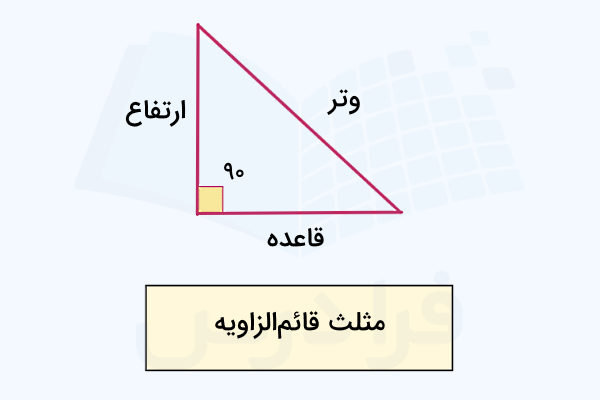
قضیه فیثاغورس در مثلث قائم الزاویه چیست؟

یکی از ویژگی‌های مخصوص مثلث‌های قائم الزاویه، وجود رابطه بین اندازه وتر و ساق‌های این مثلث است. این رابطه با عنوان قضیه فیثاغورس شناخته می‌شود. مثلث ABC را در نظر بگیرید.

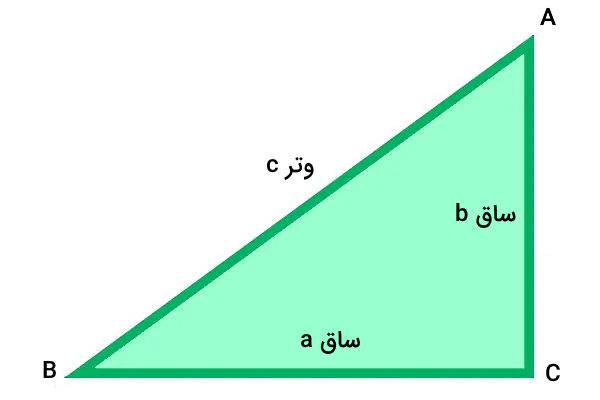
بر اساس قضیه فیثاغورس، اگر زاویه گوشه C در مثلث بالا برابر ۹۰ درجه باشد، مجذور وتر برابر جمع مجذور ساق‌ها است. عبارت جبری این قضیه به صورت زیر نوشته می‌شود:

$$c^2 = a^2 + b^2$$

• c: وتر
• a: یکی از ساق‌ها
• b: ساق دیگر

قضیه فیثاغورس، امکان محاسبه محیط مثلث قائم الزاویه با داشتن دو ضلع را فراهم می‌کند. در صورت مجهول بودن اندازه یکی از ضلع‌ها، کافی است آن را با استفاده از قضیه فیثاغورس حساب کرد و در فرمول محیط قرار داد.

مثال

اندازه دو ضلع عمود بر هم در مثلث قائم‌الزاویه‌ای برابر ۶ و ۸ است. محیط این مثلث را حساب کنید.

پاسخ

در این مثلث اندازه زاویه یکی از گوشه‌ها برابر ۹۰ درجه است. بنابراین این مثلث به عنوان یک مثلث قائم الزاویه در نظر گرفته می‌شود. دو ضلع متصل به زاویه قائمه، ساق‌های مثلث هستند. برای محاسبه محیط، به اندازه هر سه ضلع مثلث نیاز داریم. از این‌رو، قضیه فیثاغورس را برای مثلث قائم الزاویه بالا می‌نویسیم:

$$c^2 = a^2 + b^2$$

• c: وتر
• a: اندازه یکی از ساق‌ها برابر ۶
• b: اندازه ساق دیگر برابر ۸

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم:

$$c^2 = 6^2 + 8^2$$

$$c^2 = 36 + 64$$

$$c^2 = 100$$

$$c = \sqrt {100}$$

$$c = 10$$

اندازه وتر برابر ۱۰ است. اکنون که اندازه هر ضلع مثلث قائم الزاویه را داریم، محیط آن را توسط فرمول زیر محاسبه می‌کنیم:

$$P = a + b + c$$

• P: محیط
• a: اندازه یکی از ساق‌ها برابر ۶
• b: اندازه ساق دیگر برابر ۸
• c: اندازه وتر برابر ۱۰

$$P = 6 + 8 + 10$$

$$P = 24$$

در نتیجه، محیط مثلث قائم الزاویه برابر ۲۴ است.

فرمول محیط مثلث قائم الزاویه با دو ساق

مطابق با قضیه فیثاغورس، اندازه وتر مثلث قائم الزاویه برابر است با:

$$c^2 = a^2 + b^2$$

$$c = \sqrt { a^2 + b^2}$$

اگر عبارت بالا را در فرمول محیط مثلث قرار دهیم، فرمول محیط مثلث قائم الزاویه با دو ساق به دست می‌آید:

$$P = a + b + \sqrt { a^2 + b^2}$$

• P: محیط
• a: اندازه یکی از ساق‌ها
• b: اندازه ساق دیگر

مثال

محیط یک مثلث قائم الزاویه با دو ساق به اندازه‌های ۱۲ و ۵ را محاسبه کنید.

پاسخ

به منظور تعیین محیط این مثلث، فرمول مخصوص محیط مثلث قائم الزاویه با دو ساق را می‌نویسیم:

$$P = a + b + \sqrt { a^2 + b^2}$$

• P: محیط
• a: اندازه یکی از ساق‌ها
• b: اندازه ساق دیگر

$$P = 12 + 5 + \sqrt { 12^2 + 5^2}$$

$$P = 17 + \sqrt { 144 + 25}$$

$$P = 17 + \sqrt { 169}$$

$$P = 17 + 13$$

$$P = 30$$

در نتیجه، محیط مثلث برابر ۳۰ است.

محیط مثلث متساوی الساقین قائم الزاویه

در صورتی که اندازه‌های ساق یک مثلث قائم الزاویه مساوی باشند، یک شکل خاص با عنوان مثلث متساوی الساقین قائم الزاویه به وجود می‌آید:

فرمول محیط مثلث متساوی الساقین به صورت زیر نوشته می‌شود:

$$P = 2a + c$$

بر اساس قضیه فیثاغورس، می‌توانیم فرمول بالا را به فرمول مخصوص محیط مثلث متساوی الساقین قائم الزاویه تبدیل کنیم. این فرمول عبارت است از:

$$P = 2a + \sqrt {a^2+a^2}$$

$$P = 2a + \sqrt {2a^2}$$

$$P = 2a + a\sqrt {2}$$

به این ترتیب، تنها با دانستن اندازه ساق مثلث متساوی الساقین قائم الزاویه، می‌توان محیط آن را به دست آورد.

مثال

محیط یک مثلث متساوی الساقین قائم الزاویه به ساق ۵ را حساب کنید. (رادیکال ۲ را برابر ۱/۴ در نظر بگیرید.)

پاسخ

فرمول محیط این مثلث عبارت است از:

$$P = 2a + a\sqrt {2}$$

• P: محیط
• a: اندازه ساق برابر 5

$$P = (2 \times 5) + (5\sqrt {2})$$

$$P = (10) + (5 \times 1.4)$$

$$P = (10) + (7)$$

$$P = 17$$

در نتیجه محیط مثلث برابر ۱۷ است.

حل مثال از محاسبه محیط مثلث قائم الزاویه

در این بخش به حل چند مثال دیگر برای آشنایی بهتر با نحوه محاسبه محیط مثلث‌های قائم الزاویه می‌پردازیم.

مثال ۱

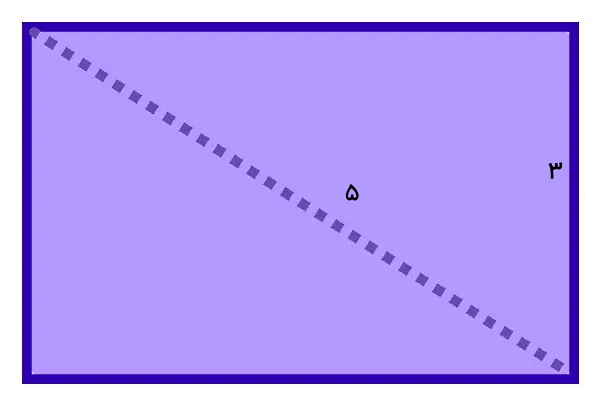
در تصویر قطر یک مستطیل را رسم کرده‌ایم. اگر اندازه عرض مستطیل برابر ۳ و اندازه قطر آن برابر ۵ باشد، محیط هر بخش مستطیل و محیط کل مستطیل چقدر است؟

پاسخ

مستطیل شکلی با ۴ ضلع و ۴ گوشه قائمه است. از این‌رو، با رسم قطر، این شکل به دو مثلث قائم الزاویه مساوی تبدیل می‌شود. عرض مستطیل، یکی از ساق‌ها و قطر آن، وتر مثلث‌های قائم الزاویه است. به این ترتیب، اندازه ساق و وتر مثلث را داریم. اکنون با استفاده از قضیه فیثاغورس، اندازه ساق دیگر را حساب می‌کنیم:

$$c^2 = a^2 + b^2$$

• c: اندازه وتر برابر ۵
• a: اندازه یکی از ساق‌ها برابر ۳
• b: اندازه ساق دیگر

$$5^2 = 3^2 + b^2$$

$$25 = 9 + b^2$$

$$b^2 = 25 - 9$$

$$b^2 = 16$$

$$b = 4$$

اندازه ساق دیگر مثلث‌های قائم الزاویه (طول مستطیل) برابر ۴ است. جمع این عدد با اندازه ساق اول (۳) و وتر (۵)، محیط هر یک از مثلث‌های قائم الزاویه است:

$$P = a + b + c$$

• P: محیط
• a: اندازه یکی از ساق‌ها برابر ۳
• b: اندازه ساق دیگر برابر ۴
• c: اندازه وتر برابر ۵

$$P = 3 + 4 + 5$$

$$P = 12$$

محیط هر مثلث برابر 12 است. محیط مستطیل نیز از جمع اندازه ضلع‌های آن به دست می‌آید:

عرض + طول + عرض + طول = محیط مستطیل

(عرض) $$\times$$ 2 + (طول) $$\times$$ 2 = محیط مستطیل

(طول + عرض) $$\times$$ 2 = محیط مستطیل

(4 + 3) $$\times$$ 2 = محیط مستطیل

(7) $$\times$$ 2 = محیط مستطیل

14 = محیط مستطیل

بنابراین، محیط مستطیل برابر ۱۴ است.

مثال ۲

تصویر زیر، سه مثلث متساوی الاضلاع، متساوی الساقین و قائم الزاویه را نمایش می‌دهد. محیط هر یک از این مثلث‌ها را تعیین کرده و با هم مقایسه کنید. چه نتیجه‌ای از نتایج به دست آمده می‌گیرید.

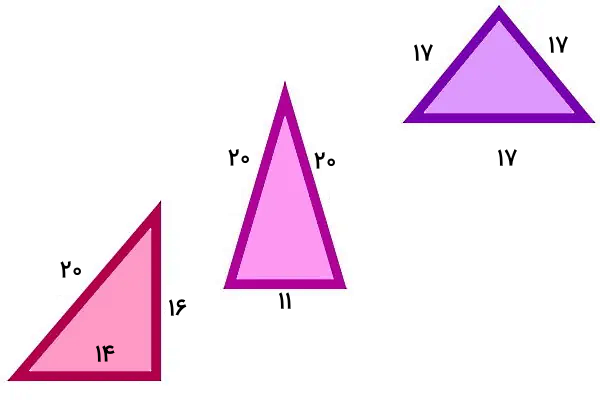
محیط مثلث متساوی الاضلاع از رابطه زیر محاسبه می‌شود:

اندازه یک ضلع × 3 = محیط مثلث متساوی الاضلاع

17 × 3 = محیط مثلث متساوی الاضلاع

51 = محیط مثلث متساوی الاضلاع

محیط مثلث متساوی الساقین، از رابطه زیر به دست می‌آید:

قاعده + (ساق × 2) = محیط مثلث متساوی الساقین

11 + (20 × 2) = محیط مثلث متساوی الساقین

11 + (40) = محیط مثلث متساوی الساقین

51 = محیط مثلث متساوی الساقین

برای مثلث قائم الزاویه نیز از رابطه زیر استفاده می‌کنیم:

ساق سوم + ساق دوم + ساق اول = محیط مثلث قائم الزاویه

20 + 14 + 16 = محیط مثلث قائم الزاویه

51 = محیط مثلث قائم الزاویه

محیط‌های هر سه مثلث نمایش داده شده در تصویر با هم برابر هستند. از این مثال نتیجه می‌گیریم که شکل‌های مختلف با اندازه ضلع‌های متفاوت می‌توانند دارای محیط یکسان باشند.

محاسبه آنلاین محیط مثلث قائم الزاویه

یکی از روش‌های محاسبه محیط مثلث قائم الزاویه، استفاده سایت‌های اینترنتی نظیر سایت گوگل، سایت Calculator.net (+) و سایت Omnicalculator (+) است. در سایت گوگل، اگر عبارتی نظیر «right triangle perimeter» را جستجو کنید.

با این کار، کادری مشابه تصویر زیر در ابتدای صفحه نتایج نشان داده می‌شود:

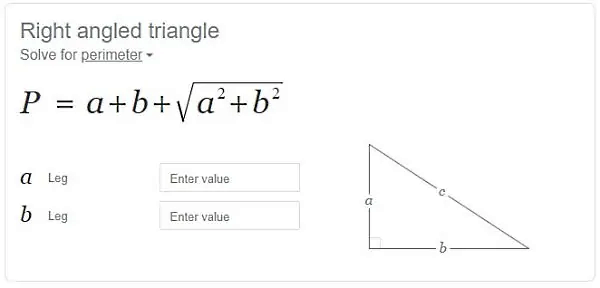
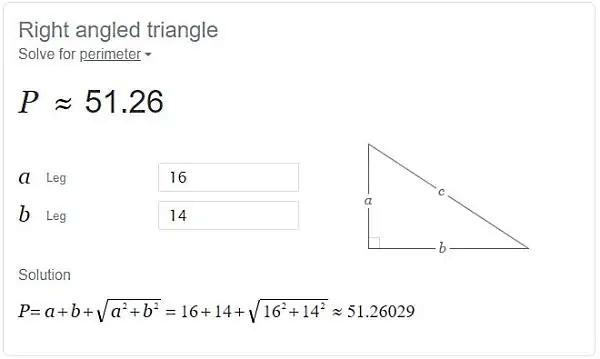
با وارد کردن اندازه یکی از ساق‌ها در کادر مقابل عنوان «a Leg» و اندازه ساق دیگر در کادر مقابل «b Leg»، محیط مثلث به نمایش در می‌آید. به عنوان مثال، اگر اعداد ۱۶ و ۱۴ را به ترتیب در کادرهای مذکور وارد کنیم، نتیجه محاسبه محیط مثلث مانند تصویر زیر نشان داده می‌شود:

سوالات متداول در رابطه مثلث قائم الزاویه و محیط آن

در این بخش، به برخی از سوالات پرتکرار در رابطه محیط مثلث‌های قائم الزاویه، به صورت خلاصه پاسخ می‌دهیم.

تعریف محیط مثلث قائم الزاویه چیست؟

محیط مثلث قائم الزاویه، اندازه دور آن است.

محیط مثلث قائم الزاویه چگونه بدست می آید؟

محیط مثلث قائم الزاویه، از جمع اندازه سه ضلع آن به دست می‌آید.

عبارت جبری محیط مثلث قائم الزاویه چیست؟

فرمول ریاضی یا عبارت جبری محاسبه مثلث قائم الزاویه، P=a+b+c است. a و b، اندازه ساق‌ها و c، اندازه وتر را نمایش می‌دهد.

فرمول محیط مثلث قائم الزاویه بر اساس قضیه فیثاغورس چیست؟

فرمول محیط مثلث قائم الزاویه بر اساس قضیه فیثاغورس به صورت P=a+b+√(a2+b2) نوشته می‌شود. a، اندازه یکی از ساق‌ها و b، اندازه ساق دیگر را نمایش می‌دهد.

فرمول محیط مثلث قائم الزاویه متساوی الساقین با ساق چیست؟

فرمول محیط مثلث قائم الزاویه متساوی الساقین، P=2a+a√2 است. a، اندازه ساق را نمایش می‌دهد.