ماتریس دوران — به زبان ساده

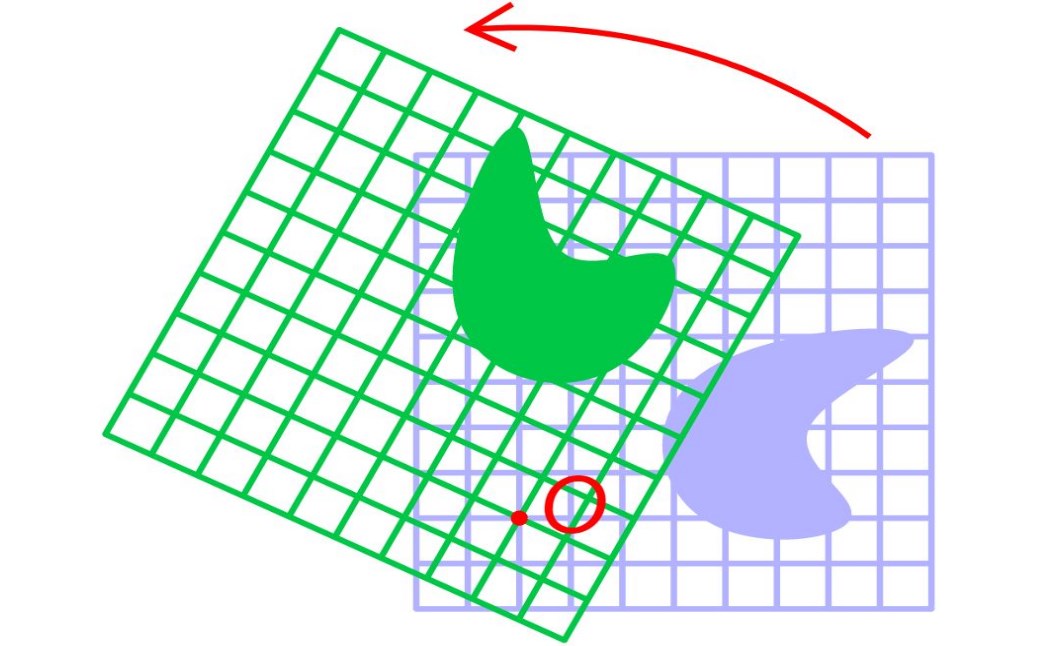
در مطلبی در مجله فرادرس نگاشت انقباضی و کاربرد آن را در معادلات کپلر توضیح دادیم. از این رو در این مطلب قصد داریم تا نوعی دیگر از نگاشت را در قالب ماتریس دوران توضیح دهیم. با استفاده از ماتریس دوران می‌توان معادلات اشکال دوران‌یافته را به شکلی ساده‌تر نوشته و نوع آن‌ها را نیز تشخیص داد.

ماتریس دوران

در ریاضیات، دوران محور‌ها یا مقاطع به مسائلی در فضای دوبعدی گفته می‌شود که در آن دستگاه مختصات $$ x y $$ به اندازه $$ \theta $$ دوران یافته و به $$ x ^ { \prime } y ^ { \prime } $$ منتقل می‌شوند. توجه داشته باشید طی این دوران، مبدأ مختصات ثابت می‌ماند. بنابراین می‌توان گفت هر نقطه در دستگاه مختصات $$ x ^ { \prime } y ^ { \prime } $$ به اندازه $$ \theta $$ نسبت به دستگاه مختصات $$ x y $$ دوران کرده است. این دوران با استفاده از ماتریسی انجام می‌شود که با ضرب شدن در معادله یک شکل یا حتی نقطه، آن را دوران می‌دهد.

فیلم آموزش ساختارهای جبری، گراف ها و ماتریس ها در فرادرس

کلیک کنید

هدف استفاده از ماتریس دوران

استفاده از دستگاه‌های مختصات به منظور مطالعه منحنی‌ها و تغییرات آن‌ها، اجتناب‌ناپذیر‌ هستند. بدین منظور محور‌های مختصات در موقعیت‌هایی قرار می‌گیرند تا نسبت به منحنی در محل مناسبی قرار داشته باشند. به عنوان مثال، جهت مطالعه معادله یک بیضی و هذلولی معمولا کانون‌ها روی یکی از محور‌ها قرار گرفته و مرکز آن منطبق بر مبدا مختصات در نظر گرفته می‌شود.

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

در شکل زیر این امر نشان داده شده است.

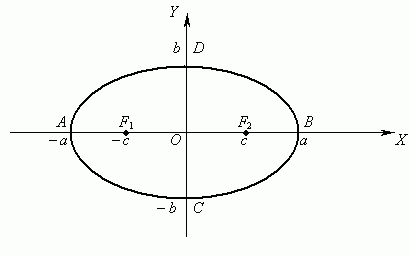
اگر منحنی نسبت به محور مختصات در موقعیت مناسبی قرار نداشته باشد، می‌توان با استفاده از نگاشت دورانی موقعیت منحنی را نسبت به محور‌ها تنظیم کرد. به این فرآیند، تبدیل مختصات گفته می‌شود. در آینده و در مطلبی مجزا در این مورد نیز صحبت خواهیم کرد.

بدست آوردن دستگاه دوران یافته

فرض کنید دستگاه اولیه $$ x y $$ به اندازه $$ \theta $$ حول مبدا، پادساعتگرد دوران کرده و دستگاه جدید را $$ x ^ { \prime } y ^ { \prime } $$ می‌نامیم. هم‌چنین فرض کنید در دستگاه $$ x y $$ مختصات قطبی نقطه $$ P $$ برابر با $$ ( r , \alpha ) $$ باشد. در این صورت در دستگاه $$ x ^ { \prime } y ^ { \prime } $$ مختصات قطبی نقطه $$ P $$ برابر با $$ ( r , \alpha - \theta ) $$ خواهد بود. مختصات اولیه برابر است با:

$$ \large {\displaystyle x = r \cos \alpha } $$

معادله ۱

$$ \large {\displaystyle y = r \sin \alpha } $$

معادله ۲

فیلم آموزش رایگان اکسل Excel – محاسبات ریاضی و ماتریسی – ویژه ناشنوایان در فرادرس

کلیک کنید

در نتیجه مختصات نقطه $$ P $$ در دستگاه مختصات $$ x ^ { \prime } $$ برابر است با:

$$ \large { \displaystyle x ^ { \prime } = r \cos ( \alpha - \theta )=r\cos \alpha \cos \theta + r \sin \alpha \sin \theta } $$
معادله ۳

$$ y ^ { \prime } = r \sin ( \alpha - \theta ) = r \sin \alpha \cos \theta - r \cos \alpha \sin \theta $$
معادله ۴

با قرار دادن معادلات ۱ و ۲ در معادلات ۳ و ۴، مختصات‌های $$ x ^ { \prime } y ^ { \prime } $$ بر حسب $$ x , y $$ برابر می‌شوند با:

$$ \large x ^ { \prime } = x \cos \theta + y \sin \theta $$
معادله ۵

$$ \large { \displaystyle y ^ { \prime } = - x \sin \theta + y \cos \theta } $$
معادله ۶

معادلات ۵ و ۶ را می‌توان به صورت ماتریسی، مطابق با عبارت زیر بیان کرد:

$$ \large \begin {pmatrix} x ^ { \prime } \\ y ^ { \prime } \end {pmatrix} = \begin {pmatrix} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{pmatrix} \begin {pmatrix} x \\ y \end {pmatrix} $$

ماتریس فوق، نشان‌دهنده تبدیل استانداردی است که مختصات اولیه را به اندازه $$ \theta $$ دوران می‌دهد. تبدیل فوق را می‌توان به صورت عکس نیز بیان کرد. در ادامه رابطه مربوط به عکس تبدیل فوق نشان داده شده است.

$$ \large { \displaystyle x = x ^ { \prime } \cos \theta - y ^ { \prime } \sin \theta } $$

$$ \large { \displaystyle y = x ^ { \prime } \sin \theta + y ^ { \prime } \cos \theta } $$

البته شکل ماتریسی تبدیل فوق را نیز می‌توان به صورت زیر بیان کرد:

$$ \large \begin {pmatrix} x \\ y \end {pmatrix} = \begin {pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end {pmatrix} \begin {pmatrix} x ^ { \prime } \\ y ^ { \prime } \end {pmatrix} $$

مثال ۱

مختصات نقطه $$ P _ 1 = ( x , y ) = ( \sqrt 3 , 1 ) $$ را پس از دوران به اندازه $$30$$ درجه بیابید.

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

کافی است $$ x , y $$ نقطه را در معادله ۵ و ۶ قرار دهید.

$$ x ^ { \prime } = \sqrt 3 \cos ( \pi / 6 ) + 1 \sin ( \pi / 6 ) = ( \sqrt 3 ) ( { \sqrt 3 } / 2 ) + ( 1 ) ( 1 / 2 ) = 2 $$
$$ y ^ { \prime } = 1 \cos ( \pi / 6 ) - \sqrt 3 \sin ( \pi / 6 ) = ( 1 ) ( { \sqrt 3 } / 2 ) - ( \sqrt 3 ) ( 1 / 2 ) = 0 $$

محور‌ها به اندازه $$ 30 $$ درجه به صورت پادساعتگرد چرخیده‌ و مختصات جدید نقطه $$ P $$ برابر با $$ P _ 1 = ( x ^ { \prime } , y ^ { \prime } ) = ( 2 , 0 ) $$ بدست آمده‌اند.

مثال ۲

مختصات نقطه $$ P _ 2 = ( x , y ) = ( 7 , 7 ) $$ پس از دوران محور‌های مختصات به اندازه $$90$$ درجه ساعتگرد را بیابید. در این مثال می‌خواهیم از روش ماتریس دوران استفاده کنیم. بنابراین مختصات نقطه در دستگاه جدید برابر است با:

$$ \large \begin {pmatrix} x ^ { \prime } \\ y ^ { \prime }
\end {pmatrix} = \begin {pmatrix} \cos ( - \pi / 2 ) & \sin( - \pi / 2 ) \\ - \sin ( - \pi / 2 ) & \cos( - \pi / 2 ) \end {pmatrix} \begin {pmatrix} 7 \\ 7 \end {pmatrix} = \begin {pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin {pmatrix} 7 \\ 7
\end {pmatrix} = \begin {pmatrix} - 7 \\ 7 \end{pmatrix} $$

دوران مقاطع مخروطی با ماتریس دوران

در مطلب مقاطع مخروطی عنوان شد که شکل کلی رابطه توصیف کننده این مقاطع به صورت زیر هستند.

$$\large { \displaystyle A x ^ { 2 } + Bx y + C y ^{ 2 } + D x + Ey  +F = 0 } $$

با استفاده از ماتریس دوران می‌توان محور‌های مختصات را دوران داده و شکل معادله فوق را ساده‌تر کرد. اگر معادلات ۵ و ۶ را در رابطه فوق قرار دهیم، شکل جدید آن به صورت زیر در می‌آید.

$$ A ^ { \prime } = A \cos ^ 2 \theta + B \sin \theta \cos \theta + C \sin ^ 2 \theta $$
$$ { \displaystyle B ^ { \prime } = 2 ( C - A ) \sin \theta \cos \theta +B ( \cos ^ { 2 } \theta - \sin ^ { 2 } \theta ) } $$
$$ {\displaystyle C ^ { \prime } = A \sin ^ { 2 } \theta - B \sin \theta \cos \theta +C \cos ^ { 2 } \theta } $$
$$ { \displaystyle D ^ { \prime } = D \cos \theta + E \sin \theta } $$ $$ { \displaystyle E ^ { \prime } = - D \sin \theta + E \cos \theta } E ^ { \prime } = - D \sin \theta + E \cos \theta $$
$$ { \displaystyle F ^ { \prime } = F } $$

اگر $$ \theta $$ به نحوی انتخاب شود که رابطه $$ \cot 2 \theta = ( A - C ) / B $$ برقرار باشد، در این صورت ضریب $$ B ^ { \prime } = 0 $$ برابر با صفر بوده و ترم $$ x ^ { \prime } y ^ { \prime } $$ نیز حذف خواهد شد. از این رو می‌توان با دوران مناسبِ محور‌های مختصات (انتخاب مقدار مناسب $$ \theta $$)، مقادیر غیرصفرِ $$ B , D , E $$ را صفر کرده و معادله اصلی را ساده‌تر کرد. برای نمونه شکل اولیه معادله بیضی زیر دارای ضرایب $$ x y $$ نیز است. با دوران دادن آن به صورت ساعتگرد و به اندازه $$ \theta $$، این ضرایب حذف خواهند شد.

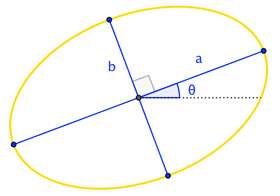
شناسایی مقاطع دوران یافته

مقطع مخروطی دوران یافته را می‌توان به صورت زیر تشخیص داد. در حقیقت علامت $$ B ^ 2 - 4 A C $$ نشان‌دهنده شکل مقطع مخروطی است.

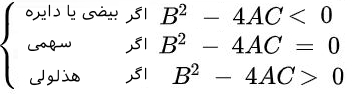
ابعاد بالاتر

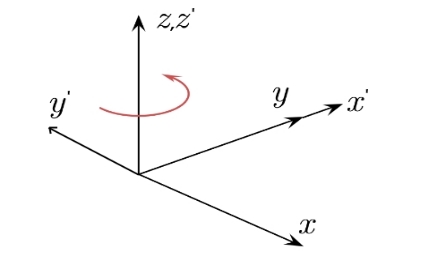
فرض کنید دستگاه مختصاتی حول محور $$ z $$ خود به اندازه $$ \theta $$، به صورت پادساعتگرد دوران کند. مختصات $$ z $$ هر نقطه تغییر نخواهد کرد و این تنها $$ z $$ و $$ y $$ هستند که تغییر خواهند کرد. فرض کنید مختصات نقطه در دستگاه اولیه برابر با $$ ( x , y , z ) $$ و در دستگاه دوران یافته برابر با $$ ( x ^ { \prime } , y ^ { \prime } , z ^ { \prime } ) $$ باشد. در این صورت رابطه بین نقاط را می‌توان با استفاده از ماتریس زیر بیان کرد:

$$ \large \begin {pmatrix} x ^ { \prime } \\ y ^ { \prime } \\ z ^ { \prime } \end {pmatrix} =\begin {pmatrix} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end {pmatrix} \begin {pmatrix} x \\ y \\ z \end {pmatrix} $$

فیلم آموزش ریاضیات گسسته در فرادرس

کلیک کنید

توجه داشته باشید که $$ A $$، ماتریسی متعامد بوده که با ماتریس همانی متفاوت است. در حالت کلی ماتریس دوران حول محور‌های $$ x $$ و $$ y $$ و $$ z $$ برابرند با:

$$ \large {\displaystyle {\begin {alignedat}{1} R _ { x } ( \theta ) &={\begin {bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & - \sin \theta \\[3pt]0&\sin \theta &\cos \theta \\[3pt] \end {bmatrix} } \\[6pt] R _ { y } ( \theta )&={\begin{bmatrix}\cos \theta &0&\sin \theta \\[3pt] 0 & 1 & 0 \\[3pt]-\sin \theta & 0 & \cos \theta \\\end{bmatrix}}\\[6pt]R_{z}(\theta ) & ={\begin {bmatrix} \cos \theta &-\sin \theta &0\\[3pt]\sin \theta &\cos \theta &0\\[3pt]0&0&1\\\end {bmatrix}}\end{alignedat}}} $$

برای نمونه فرض کنید میخواهیم دستگاه مختصات را حول محور $$ z $$ به اندازه 90 درجه دوران دهیم. در این صورت داریم:

$$ \large { \displaystyle R _ { z } ( 90 ^ { \circ } ){ \begin {bmatrix} 1 \\ 0 \\ 0 \\ \end {bmatrix} } = { \begin {bmatrix} \cos 90 ^ { \circ } & \sin 90 ^ { \circ } & 0 \\ -\sin 90^{\circ }&\quad \cos 90 ^ { \circ }&0\\0&0&1\\\end{bmatrix}}{ \begin {bmatrix}1\\0\\0\\\end{bmatrix} } ={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix} } ={\begin{bmatrix}0\\1\\0\\\end{bmatrix} } } $$

در حالتی عمومی‌تر فرض کنید دستگاه‌ مختصاتی حول محور‌های $$ x $$ و $$ y $$ و $$ z $$ به ترتیب به اندازه $$ \gamma $$ و $$ \beta $$ و $$ \alpha $$ دوران می‌کند. در این صورت ماتریس دوران برابر است با:

$$ \large { \displaystyle R = R _ { z } ( \alpha ) \, R _ { y } ( \beta ) \, R _ { x } ( \gamma ) } $$

در حالتی کلی فرض کنید $$ A $$ ماتریس دوران مربوط به فضایی $$ n $$ بعدی باشد. در این صورت مولفه‌های روی قطر ماتریس $$ A $$ آن برابر است با:

$$ \large a _ { i i } = a _ { j j } = \cos \theta $$

هم‌چنین مولفه‌های غیرقطری نیز مطابق با رابطه زیر بدست خواهند آمد.

$$ \large a _ { i j } = - a _ { j i } = \sin \theta $$

مثال ۳

مختصات نقطه $$ P _ 3 = ( w , x , y , z ) = ( 1 , 1 , 1 , 1 ) $$ را پس از دوران حول محور $$ w $$ به اندازه $$ \theta _ 3 = \pi / 12 $$ بدست آورید.

همان‌طور که می‌دانید این نقطه مربوط به یک فضای چهاربعدی است. مختصات نقطه نیز با استفاده از ماتریس دوران برابر است با:

$$ \begin{pmatrix} w ^ { \prime } \\x ^ { \prime } \\y ^ { \prime } \\z ^ { \prime } \end {pmatrix} =\begin{pmatrix} \cos ( \pi / 12 ) & 0 & 0 & \sin( \pi / 12 ) \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\- \sin( \pi / 12 ) & 0 & 0 & \cos ( \pi / 12 ) \end {pmatrix} \begin {pmatrix} w \\ x \\ y \\z\end{pmatrix} $$

$$ \approx \begin {pmatrix} 0.96593 & 0.0 & 0.0 & 0.25882 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\- 0.25882 & 0.0 & 0.0 & 0.96593 \end {pmatrix} \begin {pmatrix} 1.0 \\1.0 \\1.0 \\1.0\end{pmatrix} = \begin{pmatrix}1.22475 \\1.00000 \\1.00000 \\0.70711\end{pmatrix} $$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• مجموعه آموزش‌های ریاضی و فیزیک
• ماتریس‌ها — به زبان ساده
• ضرب ماتریس‌ها – به زبان ساده
• تعریف مقطع مخروطی و مفاهیم مرتبط با آن - به زبان ساده

^^