لاپلاس تابع پله — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در مطالب گذشته وبلاگ فرادرس در مورد مفاهیم لاپلاس و روش‌های محاسبه آن برای توابع مختلف صحبت شد. از این رو در این مطلب قصد داریم تا نوع خاصی از لاپلاس تحت عنوان لاپلاس تابع پله را محاسبه کنیم. این توابع در مباحث مهندسی برق و کنترل کاربرد بسیاری دارند.

تابع پله

قبل از توضیح در مورد نحوه بدست آوردن لاپلاس توابع پله‌ای، در ابتدا باید با این نوع از توابع آشنا باشید. در حالتی کلی یک تابع پله‌ای را می‌توان در قالب تابعی دو ضابطه‌ای به‌صورت زیر تعریف کرد.

$$ { u _ c } \left ( t \right ) = \left \{ { \begin {array} {*{20} { l } } 0 &{ { \mbox {if } } t < c } \\ 1 & { { \mbox{if } } t \ge c } \end {array}} \right.$$

فیلم آموزش معادلات دیفرانسیل به همراه حل سوالات آزمون کارشناسی ارشد در فرادرس

کلیک کنید

در ادامه شکل چنین تابعی نشان داده شده است.

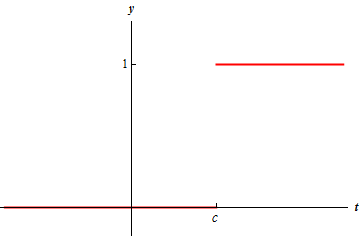
چنین توابعی را می‌توان با استفاده از ضوابط زیر نیز توصیف کرد.

$$ { u _ c } \left ( t \right ) = u \left ( { t - c } \right ) = H \left ( { t - c } \right ) $$

همان‌طور که احتمالا شما نیز متوجه شده‌اید، تابع پله‌ای را می‌توان همچون یک کلید در نظر گرفت. در حقیقت از لحظه اولیه تا زمان $$ t = c $$ کلید، باز و از این زمان به بعد کلید بسته می‌شود. اما این سوال مطرح می‌شود که چگونه می‌توان با استفاده از این تابع مقادیر ثابت بزرگ‌تری را بدست آورد؟ برای نمونه فرض کنید مقدار ثابت برابر با $$ - 4 $$ یا $$ 7 $$ باشد. بدین منظور کافی است تا تابع پله‌ای را در این اعداد ثابت ضرب کرد. حال فرض کنید می‌خواهیم کارکرد کلید را عکس کنیم. در حقیقت در زمان $$ t = c $$ کلید باز شده و تا قبل از آن کلید متصل باشد. در این صورت می‌توان از تابع زیر استفاده کرد.

$$ 1 - { u _ c } \left ( t \right ) = \left \{ { \begin {array} {*{20} { l } } { 1 - 0 = 1 } & { { \mbox {if } } t < c } \\ { 1 - 1 = 0 } & { { \mbox {if } } t \ge c } \end {array} } \right. $$

حال با ضرب کردن تابع پله ارائه شده در بالا، کارکرد معکوس ارائه شده، نیز $$ 3 $$ برابر می‌شود.

$$ 3 - 3 { u _ c } \left ( t \right ) $$

البته تابع پله‌ای، شکل‌هایی پیچیده‌تر نیز دارند که در مثال زیر ارائه شده‌اند. برای نمونه تابع زیر در $$ 4 $$ بازه مختلف، $$ 4 $$ مقدار مختلف را به عنوان خروجی اختیار خواهد کرد.

$$ f \left ( t \right ) = \left \{ { \begin {array}{*{20}{l}}{ - 4 } &{ \hspace {0.25in} { \mbox {if } } t < 6 } \\ {25} & {\hspace{0.25in}{\mbox {if } } 6 \le t < 8 } \\ { 16 } & { \hspace{0.25in}{\mbox{if }}8 \le t < 30 } \\ { 1 0 } & { \hspace {0.25in} { \mbox {if } } t \ge 30 } \end{array}} \right. $$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

تاکنون توابعی پله‌ای را معرفی کردیم که خروجی آن‌ها ثابت هستند. اما در مواردی ممکن است بخشی از یک تابع پله‌ای، الزاما عددی ثابت نباشد. برای نمونه تابعی را در نظر بگیرید که شکل آن به‌صورت زیر است.

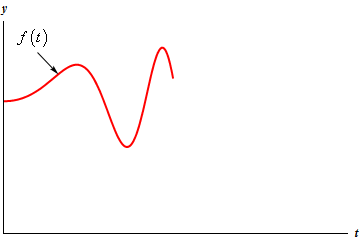
فرض کنید می‌خواهیم تابع فوق را از مبدا مشخصی تعریف کنیم. برای نمونه این کلید از زمان $$ t = c $$ بسته می‌شود. در این صورت کافی است تابع را دو ضابطه‌ای کرده و به‌جای $$ t $$، در معادله، $$ t - c $$ را قرار داد. در این صورت شکل تابع پله‌ای نیز به‌صورت زیر در خواهد آمد.

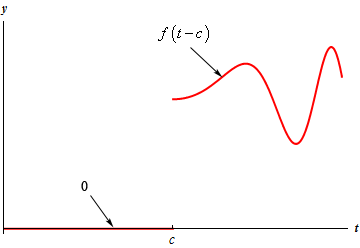
ضابطه این تابع را نیز می‌توان با ضرب کردن تابع متغیر در تابع پله‌ای بدست آورد.

$$ \begin {equation} g \left ( t \right ) = { u _ c } \left ( t \right ) f \left ( { t - c } \right ) \end {equation} $$

لاپلاس تابع پله

حال می‌خواهیم تبدیل لاپلاس تابع معرفی شده در بالا را بدست آوریم. با توجه به تعریف لاپلاس، تبدیل لاپلاس تابع پله‌ای بیان شده، با استفاده از انتگرال زیر بدست می‌‌آید.

$$ \begin {align*} \mathcal { L } \left \{ { { u _ c } \left ( t \right ) f \left ( { t - c } \right ) } \right \} & = \int _ { { \, 0 } } ^ { { \, \infty } }{ { { { \bf {e} } ^ { - s \, t } } { u _ c } \left ( t \right ) f \left ( { t - c } \right ) \, d t } } \\ & = \int _ { { \, c } } ^ { { \, \infty } } { { { { \bf { e } } ^ { - s \, t } } f \left ( { t - c } \right ) \, d t } } \end {align*} $$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

به‌منظور محاسبه انتگرال فوق می‌توان از این حقیقت استفاده کرد که مقدار تابع به ازای $$ t < c $$ صفر و به ازای مقادیر بزرگ‌تر از $$ c $$ نیز برابر با ۱ است. از این رو می‌توان از تغییر متغیر $$ u = t – c $$ استفاده کرده و نهایتا انتگرال فوق را به‌صورت زیر بازنویسی کرد.

$$ \begin {align*} \mathcal { L } \left \{ { { u _ c } \left ( t \right ) f \left ( { t - c } \right ) } \right \} & = \int _ { { \, 0 } } ^ { { \, \infty } } { { { { \bf { e } } ^ { - s \left ( { u + c } \right ) } } f \left ( u \right ) \, d u } } \\ & = \int _ { { \, 0 } } ^ { { \, \infty } } { { { { \bf { e } } ^ { - s \, u } } { { \bf { e } } ^ { - c \, s } } f \left ( u \right ) \, d u } } \end {align*} $$

همان‌طور که مشاهده می‌کنید در ترم دوم تابع نمایی $$ u $$ وجود ندارد؛ از این رو می‌توان آن را از زیر انتگرال خارج کرد. توجه داشته باشید که بازه‌های انتگرال نیز باید با توجه به تغییر متغیر در نظر گرفته شده بدست آیند. نهایتا هدف محاسبه انتگرال زیر می‌شود.

$$ \mathcal { L } \left \{ { { u _ c } \left ( t \right ) f \left ( { t - c } \right ) } \right \} = { { \bf { e } } ^ { - c \, s } } \int _ { { \, 0 } } ^ { { \, \infty } } { { { { \bf {e} } ^ { - s \, u } } f \left ( u \right ) \, d u } } $$

بدیهی است که ترم انتگرال در عبارت فوق، نشان‌دهنده لاپلاس تابع $$ f ( t ) $$ است. در نتیجه لاپلاس تابع پله‌ای فوق برابر است با:

$$ \large \begin {equation} \mathcal { L } \left \{ { { u _ c } \left ( t \right ) f \left ( { t - c } \right ) } \right \} = { { \bf { e } } ^ { - c \, s } } F \left ( s \right ) \end {equation} $$
رابطه ۱

با توجه به لاپلاس بدست آمده در بالا می‌توان رابطه معکوس زیر را نیز بیان کرد:

$$ \begin {equation} { \mathcal { L } ^ { \,\, - 1 } } \left \{ { { { \bf { e } } ^ { - c \, s } } F \left ( s \right ) } \right \} = { u _ c } \left ( t \right ) f \left ( { t - c } \right ) \end {equation} $$

با توجه به رابطه ۱، لاپلاس $$ u _ c ( t ) $$ را می‌توان به‌صورت زیر بدست آورد.

$$ \mathcal { L } \left \{ { { u _ c } \left ( t \right ) } \right \} = \mathcal { L } \left \{ { {u _ c } \left ( t \right ) \, \small \bullet \, 1 } \right \} = { { \bf { e } } ^ { - c \, s } } \mathcal { L } \left \{ 1 \right \} = \frac { 1 } { s } { { \bf { e } } ^ { - c \, s } } = \frac { { { { \bf { e } } ^ { - c \, s } } } } { s } $$

نهایتا دو رابطه زیر برای بدست آوردن لاپلاس و معکوس لاپلاس، قابل بیان هستند:

$$ \begin {equation} \mathcal{L}\left\{ { { u _ c } \left( t \right)} \right \} = \frac { { { { \bf { e } } ^ { - c\, s } } } } { s } \hspace {0.25in}{ \mathcal { L } ^ { \,\, - 1 } } \left \{ {\frac { { { { \bf { e } } ^ { - c \, s } } } } { s } } \right \} = { u _ c } \left ( t \right) \end{equation} $$

مثال ۱

تبدیل لاپلاس توابع پله‌ای زیر را بدست آورید.

$$ g \left ( t \right ) = 10 { u _ { 12 } } \left ( t \right ) + 2 { \left ( { t - 6 } \right ) ^ 3 } { u _ 6 } \left ( t \right ) - \left ( { 7 - { { \bf { e } } ^ { 12 - 3 t } } } \right ) { u _ 4 } \left( t \right ) $$

$$ f \left ( t \right ) = - { t ^ 2 } { u _ 3 } \left ( t \right ) + \cos \left ( t \right ) { u _ 5 } \left ( t \right ) $$

$$ h \left ( t \right ) = \left \{ { \begin {array} {*{20} { l } }{ { t ^ 4 } } & { { \mbox{if } } t < 5 } \\ { { t ^ 4 } + 3 \sin \left ( { \frac { t } { { 10 } } - \frac { 1 } { 2 } } \right ) } & { { \mbox {if } } t \ge 5 } \end {array}} \right. $$

$$ f \left ( t \right ) = \left \{ { \begin {array} {*{20} { l } } t & { { \mbox {if } } t < 6 } \\ { - 8 + { { \left ( { t - 6 } \right ) } ^ 2 } } &{ { \mbox {if }} t \ge 6 } \end {array}} \right. $$

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

توجه داشته باشید که در تمامی این موارد، توابع را باید به‌صورت زیر بیان کرد:

$$ { u _ c } \left ( t \right ) f \left ( { t - c } \right ) $$

در مواردی که توابع مدنظر به‌صورت فوق نباشند، باید آن‌ها را به شکلی پله‌ای بازنویسی کرد.

(a): $$ g \left ( t \right ) = 10 { u _ { 12 } } \left ( t \right ) + 2 { \left ( { t - 6 } \right ) ^ 3 } { u _ 6 } \left ( t \right ) - \left ( { 7 - { { \bf { e } } ^ { 12 - 3 t } } } \right ) { u _ 4 } \left( t \right ) $$

با توجه به شکل تابع فوق، می‌توان دید که ترم اول آن به‌صورت پله‌ای است اما ترم‌های دوم و سوم، توابعی دیگر نیز با خود دارند که به‌منظور پله‌ای کردن باید آن‌ها را تغییر داد. در ترم دوم از تابع زیر استفاده شده است.

$$ f \left ( t \right ) = 2 { t ^ 3 } \hspace {0.25in} \Rightarrow \hspace {0.25in} f \left ( { t - 6 } \right ) = 2 { \left ( { t - 6 } \right ) ^ 3 } $$

در ترم سوم نیز از تابع زیر استفاده شده است.

$$ f \left ( t \right ) = 7 - { { \bf { e } } ^ { - 3 t } } \hspace {0.25in} \Rightarrow \hspace {0.25in} f \left ( { t - 4 } \right ) = 7 - { { \bf { e } } ^ { - 3 \left ( { t - 4 } \right ) } } = 7 - { { \bf {e} } ^ { 12 - 3 t } } $$

همان‌طور که مشاهده می‌کنید این توابع به ازای مقادیری ثابت انتقال یافته‌اند. با توجه به توابع منتقل شده بالا، تبدیل لاپلاس این تابع، مطابق با رابطه زیر بدست می‌آید.

$$ \begin {align*} G \left ( s \right ) & = \frac { { 10 { { \bf { e } } ^ { - 12 s } } } } { s } + { { \bf { e } } ^ { - 6 s } } \frac { { 2 \left ( { 3 ! } \right ) } } { { { s ^ { 3 + 1 } } } } - \left ( { \frac { 7 } { s } - \frac { 1 }{ { s + 3 } } } \right ) { { \bf { e } } ^ { - 4 s } } \\ & = \frac { { 10 { { \bf
{ e } } ^ { - 12 s } } } } { s } + \frac { { 12 { { \bf { e } } ^ { - 6 s } } } }{ { { s ^ { 3 + 1 } } } } - \left ( { \frac { 7 } { s } - \frac { 1 } { { s + 3 } } } \right ) { { \bf { e } } ^ { - 4 s } } \end {align*} $$

(b): $$ f \left ( t \right ) = - { t ^ 2 } { u _ 3 } \left ( t \right ) + \cos \left ( t \right ) { u _ 5 } \left ( t \right ) $$

فیلم آموزش ساختارهای جبری، گراف ها و ماتریس ها در فرادرس

کلیک کنید

محاسبه لاپلاس این تابع به نسبت مشکل‌تر است. دلیل این امر نیز آن است که ضرایب ترم‌ها به ازای مقداری ثابت منتقل نشده‌اند. ترم اول باید به اندازه ۳ و ترم دوم نیز به اندازه ۵ منتقل شوند. بدین منظور تابع فوق را به‌صورت زیر بازنویسی می‌کنیم.

$$ f \left ( t \right ) = - { \left ( { t - 3 + 3 } \right ) ^ 2 } { u _ 3 } \left ( t \right ) + \cos \left ( { t - 5 + 5 } \right ) { u _ 5 } \left ( t \right ) $$

بدیهی است که تابع باید ترم‌هایی به‌صورت $$ t - a $$ را داشته باشد که $$ a $$ نیز نشان‌دهنده مختصاتی است که از آن به بعد تابع پله غیرصفر می‌شود. نهایتا تابع بیان شده در بالا را می‌توان به‌صورت زیر بازنویسی کرد:

$$ f \left ( t \right ) = - \left ( { { { \left( { t - 3 } \right ) } ^ 2 } + 6 \left ( { t - 3 } \right ) + 9 } \right ) { u _ 3 } \left ( t \right ) + \cos \left ( { t - 5 + 5 } \right ) { u _ 5 } \left ( t \right) $$

بنابراین دو تابعی که منتقل شده‌اند، به‌صورت زیر هستند.

$$ \begin {align*} g \left( t \right) & = { t ^ 2 } + 6 t + 9 \\ g \left ( t \right ) & = \cos \left ( { t + 5 } \right ) \end {align*} $$

با محاسبه لاپلاس تابع فوق، نهایتا لاپلاس آن مطابق با رابطه زیر بدست می‌آید.

$$ F \left ( s \right ) = - \left ( { \frac { 2 } { { { s ^ 3 } } } + \frac { 6 } { { { s ^ 2 } } } + \frac { 9 } { s } } \right ) { { \bf { e } } ^ { - 3 s } } + \left ( { \frac { { s \cos \left ( 5 \right ) - \sin \left( 5 \right ) } } { { { s ^ 2 } + 1 } } } \right ) { { \bf { e } } ^ { - 5 s } } $$

(c): $$ h \left ( t \right ) = \left \{ { \begin {array} {*{20} { l } } { { t ^ 4 } } & { { \mbox {if } } 0<t < 5 } \\ { { t ^ 4 } + 3 \sin \left ( { \frac { t } { {10 } } - \frac { 1 } { 2} } \right ) } & { { \mbox{if } } t \ge 5 } \end {array}} \right. $$

شاید با توجه به شکل تابع، اولین تصور شما این باشد که با توجه به دوضابطه‌ای بودن تابع، پیچیده به‌نظر می‌رسد. اما می‌توان آن را به‌صورت پله‌ای و همان‌گونه در ادامه آمده نیز بیان کرد:

$$ \begin {align*} h \left ( t \right ) & = { t ^ 4 } + 3 { u _ 5 } \left ( t \right ) \sin \left ( { \frac { t } { { 1 0 } } - \frac { 1 } { 2 } } \right ) \\ & = { t ^ 4 } + 3 { u _ 5 } \left ( t \right ) \sin \left ( { \frac { 1 } { {1 0 } } \left ( { t - 5 } \right ) } \right ) \end {align*} $$

با توجه به این‌که عبارت $$ t ^ 4 $$ در هر دو ضابطه وجود دارد، بنابراین می‌توان به‌راحتی تابع را با تابع پله‌ای جمع زد. نهایتا لاپلاس تابع پله‌ای نوشته شده در بالا، مطابق با رابطه زیر بدست می‌‌آید.

$$ \begin {align*} H \left ( s \right ) & = \frac { { 4 ! } } { { { s ^ 5 } } } + \frac { { 3 \left ( { \frac { 1 } { {1 0 } } } \right ) { { \bf { e } } ^ { - 5 s } } } } { { { s ^ 2 } + { { \left ( { \frac { 1 } { {1 0 } } } \right ) } ^ 2} } } \\ & = \frac { { 24 } } { { { s ^ 5 } } } + \frac { { \frac { 3 }{ { 1 0 } }{{\bf { e }} ^ {‌- 5 s } } } } { { { s ^ 2 } + \frac { 1 } { { 100} } } } \end{align*} $$

(d): $$ f \left ( t \right ) = \left \{ { \begin {array} {*{20} { l } } t & { { \mbox {if } } 0<t < 6 } \\ { - 8 + { { \left ( { t - 6 } \right ) } ^ 2 } } &{ { \mbox {if }} t \ge 6 } \end {array}} \right. $$

این تابع نیز همانند تابع قبلی، دوضابطه‌ای است؛ از این رو باید آن را به‌صورت پله‌ای و همانگونه که در ادامه آمده، بازنویسی کرد.

$$ f \left ( t \right ) = t + \left ( { - 8 - t + { { \left ( { t - 6 } \right )
} ^ 2 } } \right ) { u _ 6 } \left ( t \right ) $$

بدیهی است که برای پله‌ای نوشتن تابع، باید عبارت $$ t - 6 $$ را در تابع قرار داد. در حقیقت تابع فوق را می‌توان به‌صورت زیر بیان کرد:

$$ \begin {align*} f \left ( t \right ) & = t + \left ( { - 8 - \left( { t - 6 + 6 } \right ) + { { \left ( { t - 6 } \right ) } ^ 2 } } \right ) { u _ 6 } \left ( t \right ) \\ & = t + \left ( { - 8 - \left ( { t - 6 } \right ) - 6 + { { \left ( { t - 6 } \right ) } ^ 2 } } \right ) { u _ 6 } \left ( t \right ) \\ & = t + \left ( { - 14 - \left ( { t - 6 } \right ) + { { \left ( { t - 6 } \right ) } ^ 2 } } \right ){ u _ 6 } \left ( t \right ) \end {align*} $$

همان‌طور که مشاهده می‌شود، ترم دوم، شکل انتقال یافته تابع زیر است.

$$ g \left ( t \right ) = { t ^ 2 } - t - 14 $$

نهایتا تبدیل لاپلاس پله‌ای بیان شده در بالا مطابق با عبارت زیر بدست می‌‌آید.

$$ F \left ( s \right ) = \frac { 1 } { { { s ^ 2 } } } + \left ( { \frac { 2 } { { { s ^ 3 } } } - \frac {‌ 1 } { { { s ^ 2 } } } - \frac { { 14 } } { s } } \right ){{\bf { e } } ^ { - 6 s } } $$