قضیه گرین (Green Theorem) – به زبان ساده
در این مطلب قصد داریم تا نوع خاصی از انتگرال خطی را مورد بررسی قرار دهیم. انتگرال مذکور از مرتبه اول بوده و ارتباط آن با انتگرال دوگانه بیان خواهد شد. این قضیه در مکانیک کلاسیک و خصوصا در مکانیک سیالات بسیار پرکاربرد است. منظور از عبارت قضیه در جمله قبل، «قضیه گرین» (Green Theorem) است.
صورت قضیه گرین
قضیه گرین بیان میکند که انتگرال خطیِ تابع برداری F روی مرز بستهی C برابر با انتگرال دوگانه تابع کرلِ F روی سطح محصور در آن است (سطح R). در ابتدا شکل زیر را در نظر بگیرید.
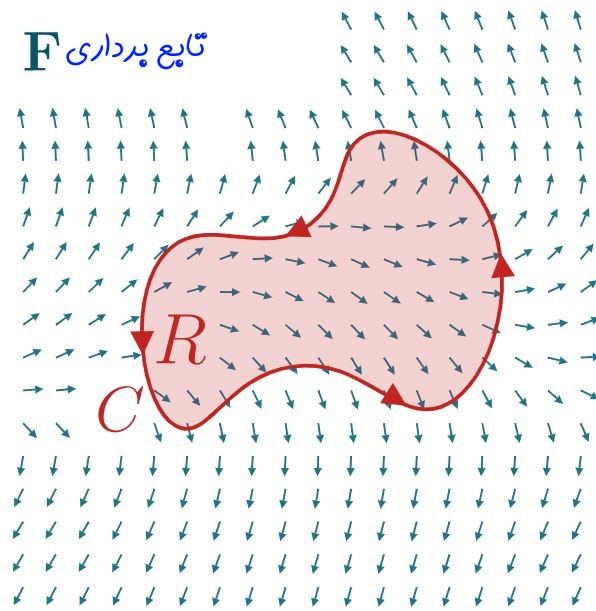
مطابق با شکل بالا، قضیه گرین برابر است با:
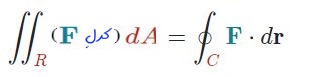
شاید سمت چپ رابطه بالا برایتان کمی گیجکننده باشد. از این رو اجازه دهید قضیه را در قالب فرمولی دیگر بیان کنیم. احتمالا تاکنون متوجه شدهاید که F یک تابع برداری -مثلا سرعت- است که مولفههایش بهصورت توابعی از x و y هستند؛ بنابراین میتوان آن را بهصورت زیر بیان کرد:
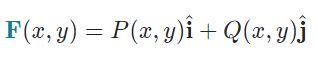
راحتتر آن است که قضیه در قالب P و Q بیان شود. قضیه گرین با فرض تابع F بهصورت بالا، برابر است با:
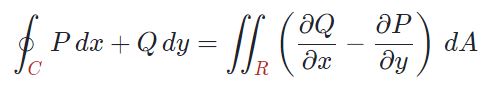
جهت یادگیری استفاده از این قضیه، مثالهایی در انتهای همین مطلب ذکر شدهاند. اما پیشنهاد ما این است که در گام نخست، مفهومِ این قضیه را درک کنید. در ادامه، با بررسی سیالِ در حال حرکت در یک محیط، مفهوم رابطه ۱ را توضیح خواهیم داد.
چرخش سیال اطراف مرز
مطابق با شکل زیر، سیالی را در نظر بگیرید که بهصورت تصادفی در یک محیط در حال حرکت است.
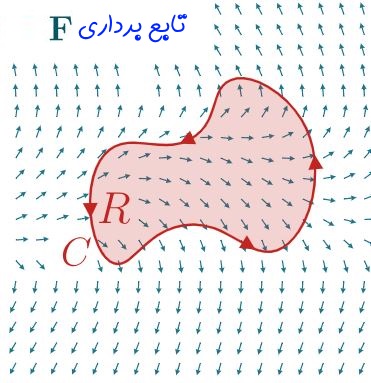
با توجه به شکل فوق، فرض کنید:
- (F(x,y تابعی برداری است که میدان سرعت سیال را در مختصاتهای مختلف ناحیه R نشان میدهد.
- R، ناحیهای محصور، درون خمی بسته است که سیال در بخشی از مسیرش، از آن عبور میکند. در حالتی ایدهآل این ناحیه میتواند یک دایره و یا هر محیط بستهی دیگری باشد.
- C، مرزِ بستهی ناحیه R محسوب میشود که مطابق با شکل ۱ بهصورت پادساعتگرد در نظر گرفته شده است. توجه داشته باشید که جهت خم در حل مسائل مهم هستند.
مفهوم انتگرال خطی
به نظر شما چطور میتوان انتگرال خطی زیر را به مسئلهی حرکت سیال مرتبط کرد.
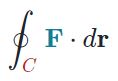
توجه داشته باشید که در این حالت، بردار دیفرانسیلی dr، برابر با جابجایی کوچک روی منحنی C در نظر گرفته میشود. با توجه به جهت منحنی، همواره این جابجایی اندک پادساعتگرد خواهد بود. جهت درک ، قایقی را در نظر بگیرید که روی مسیر C بهصورت پادساعتگرد در حال حرکت است.
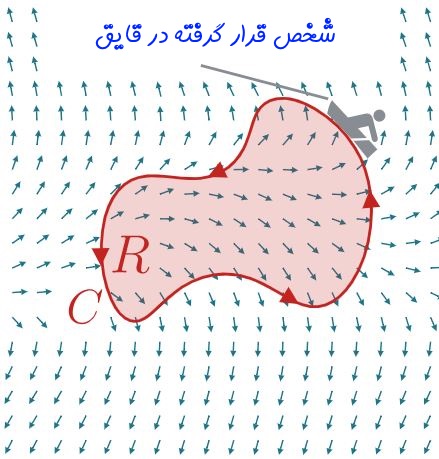
در هر نقطه از مسیر حرکتِ قایق، بردار dr نشان دهنده جابجایی اندکی است که قایق تجربه کرده. همانطور که از مفهوم ضرب داخلی میدانید، بردار dr در جاهایی که مسیر حرکتِ قایق و سیال در یک جهت باشد مثبت و اگر مسیرتان عکس هم باشد، منفی خواهد بود. در شکل زیر دو حالتِ مذکور نشان داده شدهاند.
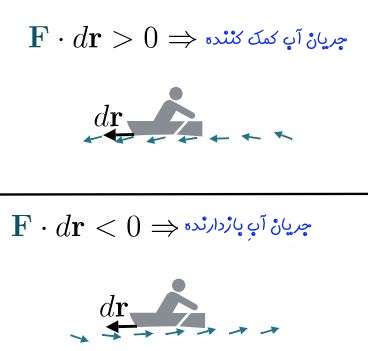
انتگرال روی مسیری بسته است. بنابراین مفهوم فیزیکیش این است که جریان آب به حرکت قایق کمک کرده یا مانع حرکت آن است. در حقیقت در لحظاتی که مسیر شما پادساعتگرد است، ضرب داخلی مثبت و جریان سیال به حرکت قایق کمک کرده؛ از طرفی لحظاتی که مسیر حرکت قایق ساعتگرد است، حاصل ضرب داخلی منفی و در نتیجه جریان آب مانع حرکت قایق است.
انتقال مرز به داخل
قضیه گرین در مورد نحوه چرخش سیال روی مرزِ R و وابستگی آن به وقایعِ درون مرز صحبت میکند. همین گذاره در مورد سطوح تشکیل دهندهی سطح اصلی نیز صادق است. در ادامه این جمله را به زبان ریاضیات توضیح خواهیم داد.
تقسیمبندی ناحیه
فرض کنید سطح R همچون شکل زیر به دو ناحیهی R1 و R2 تقسیم میشوند.
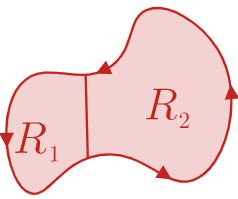
این مرزها با C1 و C2 نشان داده میشوند. بنابراین ما یک سطحِ بسته را به دو سطحِ بسته R1 و R2 تقسیم کردهایم.
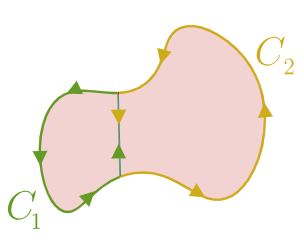
به نظر شما در این صورت حاصل جمع انتگرال خطی دو مرز برابر با چه عبارتی خواهد بود؟
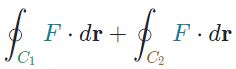
همانطور که در شکل ۲ نیز میبینید، مسیرهای C1 و C2 در مرز، خلاف جهت یکدیگر هستند. بنابراین حاصل انتگرال تابع F روی آنها نیز برابر اما علامتشان عکس هم است. انتگرال تابع F روی مرز، یکدیگر را خنثی میکنند.
استدلال بالا به این معنی است که حاصل انتگرال روی دو مسیرِ C1 و C2 برابر با انتگرال روی کل مسیر است. در حقیقت میتوان نوشت:
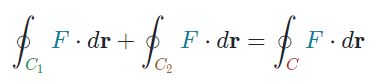
اگر مطابق با شکل زیر برای بار دوم، این ناحیه تقسیم شود، جهت مسیرهای مشترک خلاف جهت هم بوده و انتگرالِ تابع روی آنها برابر با صفر است. برای نمونه شکل ۲ را دوباره به دو قسمت تبدیل میکنیم. در این صورت ناحیه بهشکل زیر در خواهد آمد.
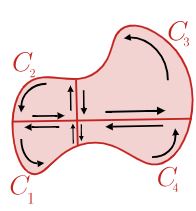
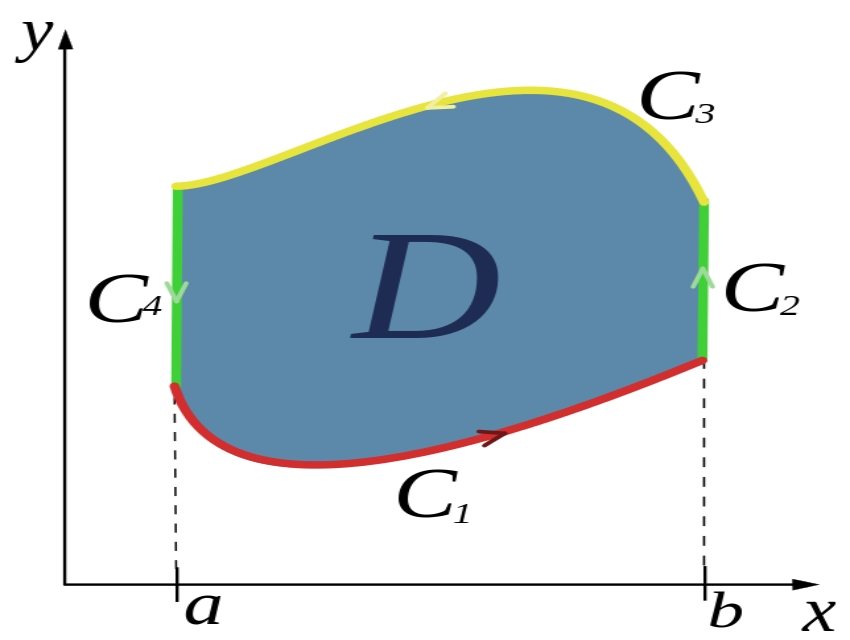
در شکل بالا ۴ مسیر بستهی C1 ,C2 ,C3 ,C4 وجود دارد که حاصل جمع انتگرال تابع F روی آنها برابر است با:
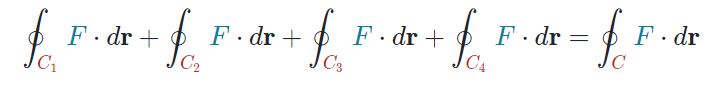
توجه داشته باشید که رابطه بالا تنها زمانی صادق است که جهت تمامی مسیرها بهصورت ساعتگرد یا پادساعتگرد و مشابه با مسیر اصلی باشند.
استدلال بالا در حالتی که مسیر به بینهایت قسمت تقسیم شود، نیز صادق خواهد بود. شکل زیر را در نظر بگیرید.
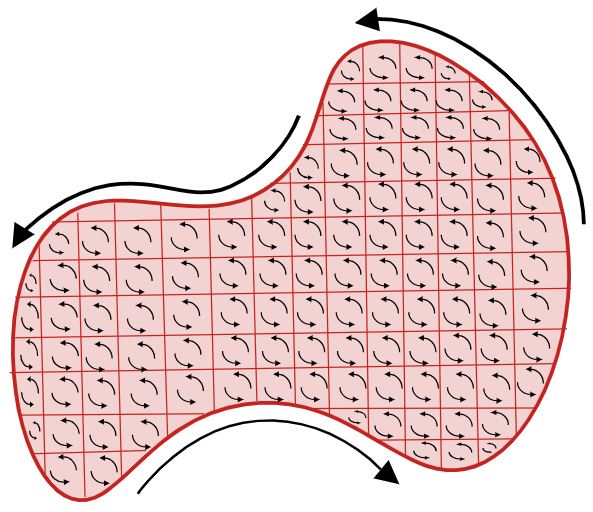
در این حالت ناحیه R به R1,...,Rn تقسیم میشود. در نتیجه مسیرهای این نواحی بهترتیب برابر با C1,....Cn هستند. در حقیقت رابطه بین انتگرالهای خطی تابع F، روی تمامی مسیرها برابر خواهند بود با:
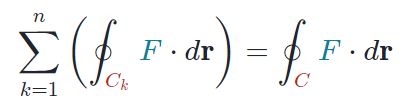
انتگرالگیری از تابع کِرل
شاید این سوال در ذهن شما مطرح شود که چرا مبحثِ تقسیمبندی نواحی مطرح شد؟ پیشنهاد ما این است که در مورد این سوال اندکی فکر کنید و سپس پاراگراف بعدی را مطالعه فرمایید!
دلیل تقسیم بندی، بیان کردن انتگرالِ خطی تابع، به شکلی متفاوت است. مطابق با شکل زیر بخشی از ناحیهی تقسیمبندی شده را در نظر بگیرید.
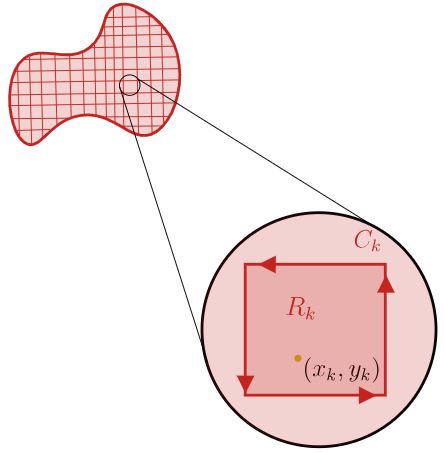
- Rk ناحیهی انتخاب شده و Ck مسیر بستهی متناظر با آن است.
- |Rk| مساحت ناحیهی Rk است که دارای مقداری بسیار اندک است.
- (xk,yk) مختصات نقطهای تصادفی در Rk است.
میزان چرخش سیال در ناحیه Rk را میتوان معادل با انتگرالِ دانست. با توجه به اینکه ناحیهی مورد بررسی، بسیار کوچگ است چرخش سیال را میتوان معادل با چرخش قایق روی مرزهای Rk دانست. اما مفهوم دیگری نیز در ریاضیات وجود دارد که با استفاده از آن میتوان میزان چرخش سیال را اندازهگیری کرد. این مفهوم کرل است.
بنابراین انتگرال خطی روی این مسیر کوچک را میتوان معادل با رابطه زیر تقریب زد.
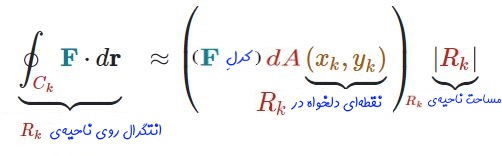
توجه داشته باشید که در استدلال بالا هرچه ناحیهی Rk کوچکتر باشد، رابطه بالا دقیقتر خواهد بود. با جمع زدن روابط بالا در تمامی ناحیهها داریم:
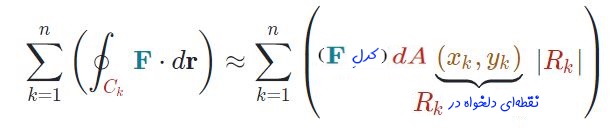
سمت راست رابطه بالا را توضیح دادیم که چگونه برابر با انتگرال خطی روی کل مسیر است. با این نتیجهگیری رابطه فوق را میتوان بهصورت زیر بازنویسی کرد.
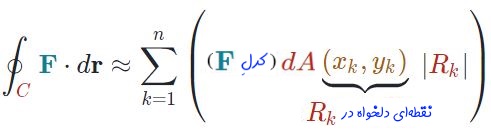
ترم چپ رابطهی بالا از ویژگیهای زیر برخوردار است:
- عبارت ضربِ کرلِ تابعِ F در مساحت بهصورت عددی اسکالر است.
- حاصل جمع، روی بینهایت Rk انجام میشود.
- برای هر قطعه، مقدار کرل در مرکز سلول محاسبه شده و در مساحت سلول ضرب میشود.
هر سه مورد بالا نشان دهندهی انتگرالِ دوگانهی کرلِ تابعِ F روی سطح است. بنابراین اگر حاصل ضرب کرلِ تابع F در مساحت را بهطور جداگانه برای تمامی مساحتها محاسبه کنیم، رابطه زیر را میتوان نوشت:

بنابراین نهایتا رابطهی ۳ را میتوان بهصورت زیر بیان کرد:
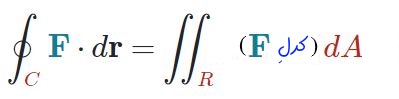
رابطهی بالا نشان دهنده قضیه گرین است. در حقیقت این قضیه میگوید حاصل جمع چرخش هرکدام از نواحی شکل زیر (سمت راست رابطهی فوق)، برابر با چرخش سیال روی مرز ناحیه (سمت چپ) است.
شکل معمول قضیه گرین
معمولا قضیه گرین را بهشکل فرمول زیر نمایش میدهند.
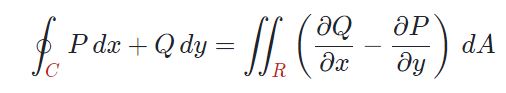
البته حقیقتا بهمنظور استفاده از قضیهی گرین، قالب فوق مناسبتر است. توجه داشته باشید که در رابطه فوق، عبارات P و Q مولفههای تابع برداری F هستند. در حقیقت شکل تابع F بهصورت زیر در نظر گرفته شده است.
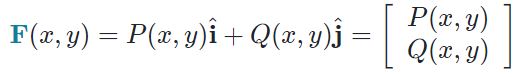
بهمنظور درک بهتر قضیه گرین پیشنهاد میکنیم به مثالهای ارائه شده در ادامه توجه فرمایید.
مثال ۱
دایرهای به شعاع ۲ را مطابق با شکل زیر در نظر بگیرید که مرکز آن در (2-,3) قرار گرفته.
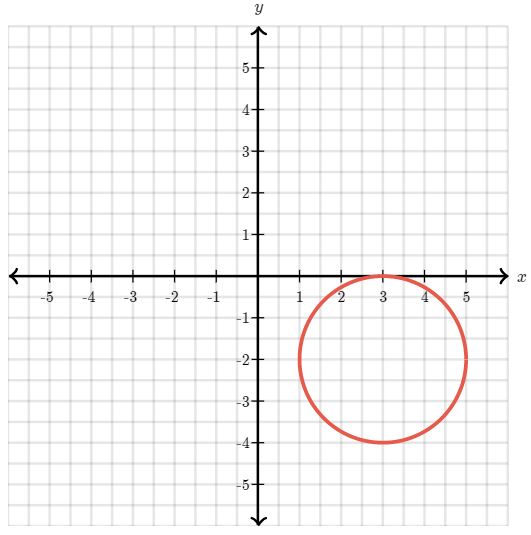
مسیر C را بهصورت پادساعتگرد در نظر بگیرید. با این فرض انتگرال زیر را محاسبه کنید.
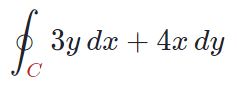
در قدم اول بایستی به ساعتگرد یا پادساعتگرد بودن منحنی توجه کنید. در قدم دوم بایستی توابع P و Q شناسایی شوند. با توجه به رابطه ۴ ضریب dx برابر با P و ضریب dy برابر با Q است. در نتیجه P برابر با 3y و Q برابر با 4x است.
در قدم سوم بایستی مشتق جزئی توابع P و Q محاسبه شوند. با محاسبه مشتق جزئی توابع مذکور داریم:
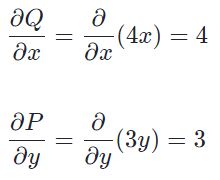
در گام چهارم مشتقات فوق را در رابطهی ۴ قرار داده و حاصل عبارت را روی مسیر مذکور بدست آورید. با انجام این کار به رابطهی زیر میرسیم.
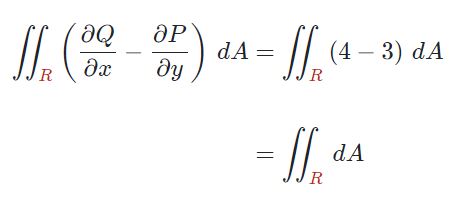
بدیهی است که حاصل انتگرال بالا روی دایره، برابر با مساحت آن است. با توجه به اینکه شعاع دایره برابر با ۲ بوده، بنابراین مساحت آن (حاصل انتگرال بالا) برابر است با:
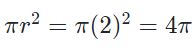
توجه داشته باشید که همواره نمیتوان به سادگی بالا از قضیه گرین استفاده کرد. در بعضی موارد، مسیر C شکل منظمی -مثل دایره- ندارد؛ در چنین مواردی استفاده از قضیه گرین به نسبت مشکلتر خواهد بود.
مثال ۲
توابعی را مطابق با روابط زیر در نظر بگیرید.
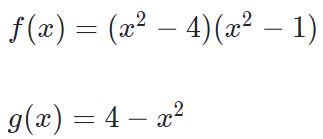
اگر دو نمودار رسم شوند، ناحیهی میان آنها بهصورت زیر خواهند بود:
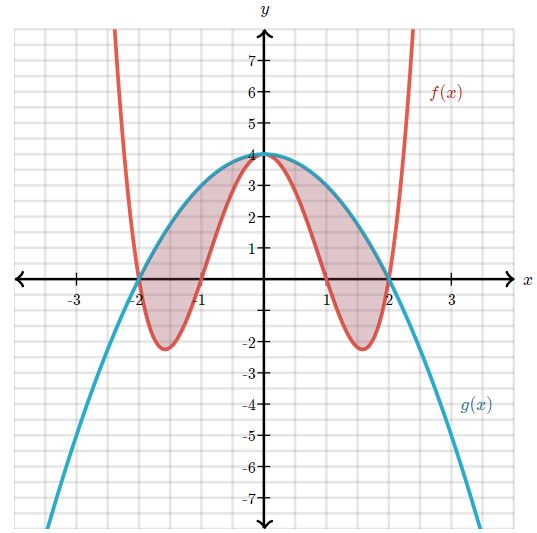
فرض کنید ناحیهی بین دو نمودار بهصورت ساعتگرد در نظر گرفته شود. در این صورت حاصل انتگرال زیر را روی منحنی D بیابید.
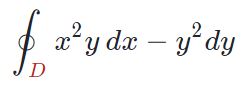
با معادلسازی دو رابطه زیر با یکدیگر، توابع (P(x,y و (Q(x,y نیز بدست میآیند.
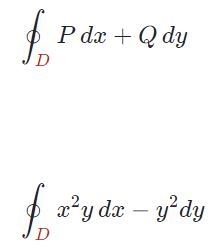
با انجام مقایسهی بالا توابع (P(x,y و (Q(x,y برابرند با:
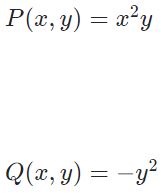
در نتیجه مشتقات جزئی توابع P و Q برابر با توابع زیر بدست میآیند.
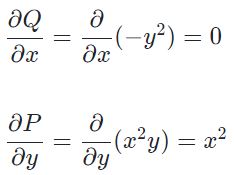
با توجه به شکل ۳، ناحیهی بین دو نمودار، بالای تابع (y=(x2-4)(x2-1 و زیر قرار میگیرد. حال بایستی سمت راست رابطه ۴ محاسبه شود. توجه داشته باشید که این رابطه، انتگرالی دوگانه با فرمت زیر است.
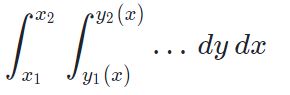
از طرفی مقدار x از ۲- تا ۲+ تغییر میکند. نهایتا با اعمال مشتقات جزئی محاسبه شده و قرار دادن آن در رابطه مربوط به انتگرال دوگانه، خواهیم داشت:

از این مرحله به بعد، با انتگرالی یگانه سروکار داریم که با محاسبه آن بهصورت زیر، پاسخ نهایی بدست میآید.
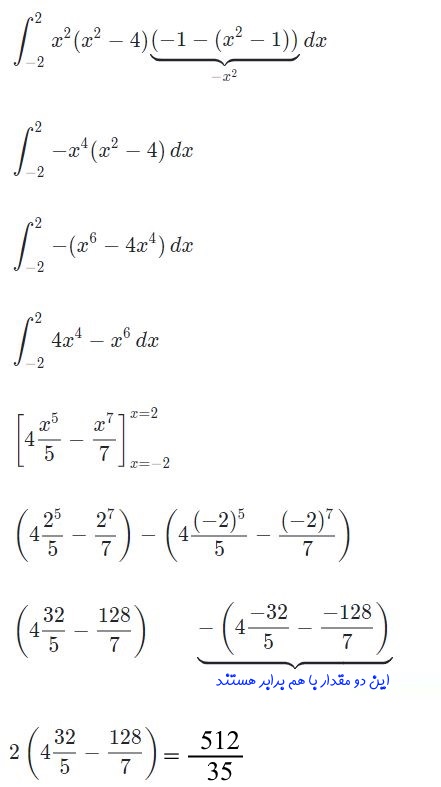
خلاصه
- با استفاده از قضیهی گرین میتوان انتگرالهای خطی را در زمانی سریعتر و در قالب انتگرالی دوگانه محاسبه کرد.
- برای پاسخ به این سوال که آیا در این مسئله قضیه گرین مناسب است؟ میتوانید دو سوال زیر را مطرح کنید.

- همچنین به مسیر C توجه کنید و در نظر داشته باشید که آیا انتگرالگیری دوگانه روی آن آسان است؟
- از نتایج قضیه گرین این است که حاصل انتگرال زیر، مساحت محصور در منحنی بستهی C را نشان محاسبه میکند.
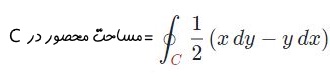
^^













سلام ممنون خوب بود شکل ها و مثال به روشن شدن مطلب کمک می کند
سلام
بسيار عالي بود. خيلي خوب و مفهومي قضيه اثبات شد.
بسيار متشکرم از زحمات شما
متشکرم از توضیخات بنیادی تون که به مادر فهم مسایل کمک میکنه…… فقط کاربردش توی الکترودینامیک رو هم باز میکردین خیلی عالی میشد دیگه
قسمت دوم ثابت نشد.فقط مشخص شد که مفهوم قسمت اول قضیه یعنی چرخش سیال..
خوب بود .ای کاش برای اون فرمول مساحت محصور هم مثال میزدین.
واقعن دستتون درد نکنه، خیلی مفید و کاربردی توضیح دادید.
بعد از این همه مدت یه جایی که بشه یک سری مفاهیم رو یاد گرفت وجود داره.
واقعن اینجا فرادرس هستش.
ممنوووووون
عالی بود حرف نداشت تازه فهمیدم این قضیه چیه!
توضیح خوب و کاربردی بود. متاسفانه در اغلب کتاب ها و کلاس ها مباحث کاربردی مطرح نمیشه و فقط ریاضی محض و غیر قابل درک هست. اما شما توضیحات کاملی دادین. ممنون
سلام-واقعا ممنون بخاطر توضیحتان
بسيار قشنگ بود ممنون
واااااقعا عالی بود من الان فهمیدم جریان چیه