شرایط مرزی الکترومغناطیسی – از صفر تا صد
در آموزشهای قبلی مجله فرادرس، درباره امواج الکترومغناطیسی و میدانهای الکتریکی و مغناطیسی صحبت کردیم. در این آموزش قصد داریم شرایط مرزی الکترومغناطیسی را بررسی کنیم.
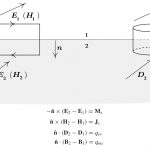
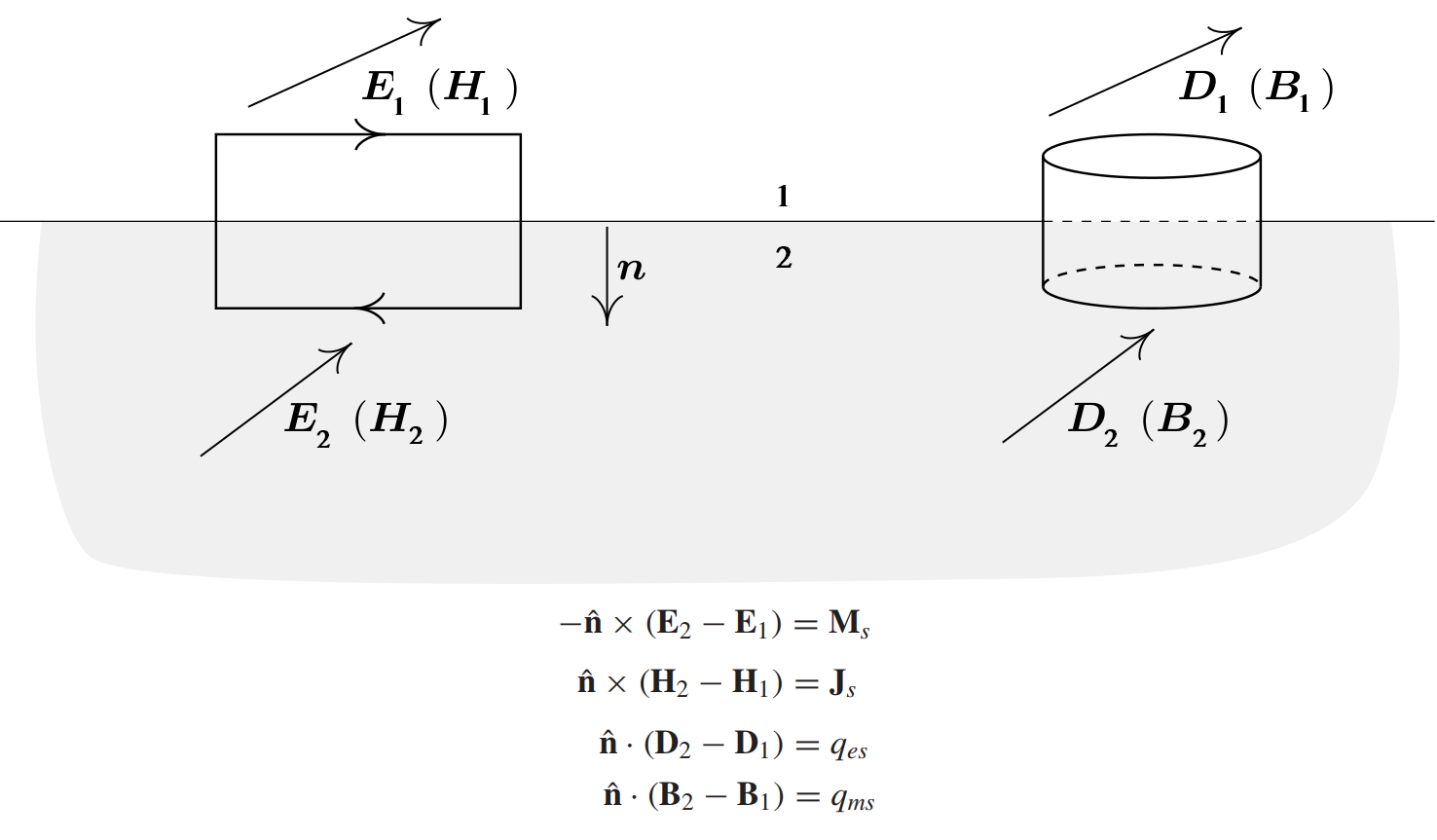
همانطور که میدانیم، میتوان از فرم دیفرانسیلی معادلات ماکسول برای حل «میدانهای برداری» (Vector Fields) استفاده کرد. بردارهای میدان و مشتقات آن، توابعی پیوسته هستند و مقدار آنها مشخص و محدود است. در طول مرز مشترک دو محیط، خواص الکتریکی ناپیوسته است و تغییر میکند. یا حتی ممکن است منبعی در طول مرز وجود داشته باشد. به این ترتیب بردارهای میدان نیز در طول مرز مشترک ناپیوسته خواهند بود. «شرایط مرزی الکترومغناطیسی» (Electromagnetic Boundary Conditions)، اندازه و جهت این بردارها را مشخص میکند.
شرایط مرزی الکترومغناطیسی
«معادلات ماکسول» (Maxwell's Equations) در حالت دیفرانسیلی خود، به صورت مشتقات بردارهای میدان در مختصات فضایی نوشته میشوند. مشتق میدان برداری در نقاط ناپیوستگی تعریف نشده است و نمیتوان از آنها برای تعریف رفتار بردار میدان در طول مرز استفاده کرد. در عوض، رفتار میدان برداری در طول مرزهای ناپیوسته باید به وسیله بردارهای میدان و نه مشتقات آن تعریف شود.
وابستگی بردار میدان به خواص الکتریکی محیط در طول مرز ناپیوستگی، مسئلهای است که ما همه روزه با آن سر و کار داریم. مثلا وقتی دستگاههایی مانند تلفن همراه، رادیو یا تلویزیون به داخل یا خارج یک محیط سربسته (مثل تونل یا یک ساختمان حفاظتشده) منتقل میشوند، گیرندگی آنها دچار اختلال میشود. با عبور موج از محیط، سیگنال دریافتی کاهش مییابد یا از بین میرود. این مسئله نتیجه تضعیف موج در عبور از محیط است. این کاهش میتواند نتیجه تغییر محیط و عبور موج از مرز نیز باشد. بهترین راه برای استنتاج شرایط مرزی الکترومغناطیسی، استفاده از معادلات ماکسول در فرم انتگرالی است. ابتدا معادله اول ماکسول را به فرم انتگرالی زیر مینویسیم:
معادله (۱)
محیط با رسانایی محدود
یک سطح مشترک بین دو محیط مختلف را در نظر بگیرید. شکل زیر این مسئله را نشان میدهد:
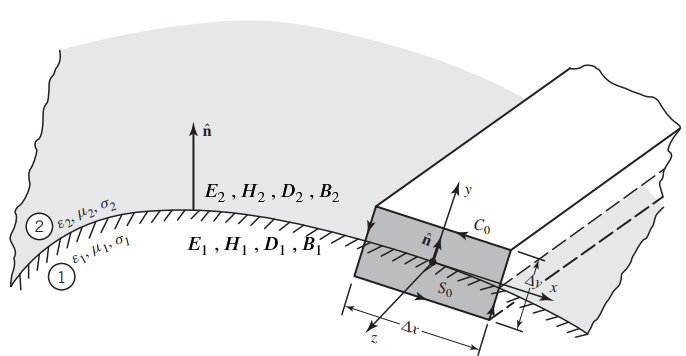
فرض کنید که هیچ بار یا منبعی روی سطح وجود ندارد و هیچ یک از دو محیط نیز هادی کامل نیست. همچنین هیچ منبعی در این دو محیط وجود ندارد. محیطهای ۱ و ۲ به ترتیب به وسیله پارامترهای سازنده خود یعنی () و () تعریف میشوند.
یک مکعب مستطیل را روی این سطح مشترک در نظر بگیرید. سطح مقطع این مکعب مستطیل است که با منحنی محدود شده است. از دستگاه مختصاتی دکارتی () برای نشان دادن ساختار محلی مستطیل استفاده شده است. در معادله (۱) اگر را روی مستطیل برابر صفر فرض کنیم، داریم:
معادله (۲)
فرض کنید ارتفاع در مستطیل را کمتر و کمتر کنیم. به همین ترتیب سطح کوچکتر و کوچکتر میشود. بنابراین انتگرال سطحی در سمت راست معادله (۲) قابل صرفنظر است. به علاوه، سهم انتگرال خطی در طول نیز ناچیز است. بنابراین در حد که ، معادله (۲) به رابطه زیر تبدیل میشود:
معادله (۳)
یا به عبارت سادهتر:
معادله (۴)
که یک بردار واحد از محیط (۱) به سمت محیط (۲) است. در معادله (۴) فرض شده است که و محدود هستند. یعنی دو محیط، هدایت محدود دارند.
در معادله (۳)، و به ترتیب مولفههای «مماسی» (Tangential) میدان الکتریکی در محیطهای اول و دوم و در طول سطح مشترک هستند. دو معادله (۳) و (۴) بیان میکنند که اگر منبع جریان مغناطیسی در سطح مرز مشترک وجود نداشته باشد، مولفههای مماسی میدان الکتریکی دو محیط در طول سطح مشترک پیوسته و با هم برابر هستند.
حال معادله دوم ماکسول را در نظر بگیرید:
معادله (۵)
اگر از یک فرآیند مشابه روی مستطیل استفاده شود، با در نظر گرفتن معادله (۵) و فرض ، میتوان نوشت:
معادله (۶)
معادله (۷)
در معادله (۷) فرض میشود که و محدود هستند. این معادله بیان میکند که مولفههای مماسی میدان مغناطیسی در طول سطح مشترک بین دو محیط که هیچ یک از آنها هادی الکتریکی کامل نیست، پیوسته است. اگر یکی از دو محیط هادی کامل باشد یا منبع جریان روی مرز دو محیط وجود داشته باشد، معادلات (4) و (7) تغییر میکنند. علاوه بر شرایط مرزی الکترومغناطیسی مربوط به مولفههای مماسی میدانهای الکتریکی و مغناطیسی، مولفههای نرمال یا «عمودی» (Normal) این دو میدان نیز به یکدیگر وابسته هستند.
حال معادله سوم ماکسول را در نظر بگیرید:
معادله (۸)
در این معادله چگالی حجمی بار الکتریکی و کل بار الکتریکی است.
حال ساختار شکل زیر را در نظر بگیرید:
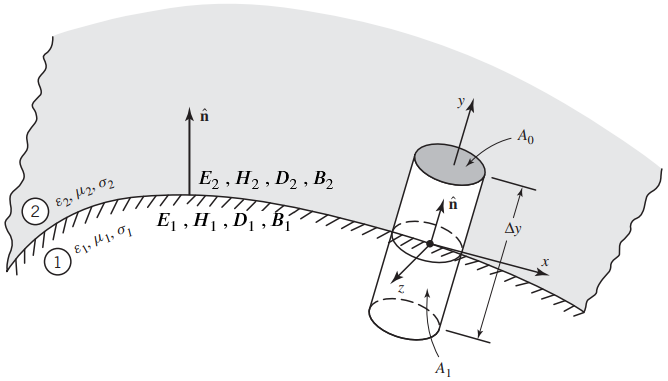
در این شکل، یک استوانه کوچک در یک نقطه معین روی مرز در نظر گرفته شده است. اگر هیچ بار یا منبعی روی مرز وجود نداشته باشد یا هیچ یک از دو محیط هادی کامل نباشند، میتوان معادله (۸) را به صورت زیر بازنویسی کرد:
معادله (10)
اگر ارتفاع استوانه را کمتر کنیم، مساحت سطح جنبی نیز کمتر میشود. بنابراین میتوان از انتگرال سطحی ناشی از صرفنظر کرد. بنابراین در حد که میتوان معادله (۱0) را به صورت زیر بازنویسی کرد:
معادله (11)
یا:
معادله (۱۲)
در معادله (۱۲) فرض شده است که و محدود هستند. در معادله (۱۱)، و مولفههای عمودی چگالی شار الکتریکی در محیطهای اول و دوم در طول سطح مشترک هستند. دو معادله (۱۱) و (۱۲) بیان میکنند که مولفههای عمودی چگالی شار الکتریکی در طول مرز مشترک بین دو محیط که هر دو هدایت محدود دارند یا هیچ منبعی وجود ندارد، پیوسته است. اگر یکی از دو محیط هادی کامل باشد یا در طول مرز مشترک منبع وجود داشته باشد، روابط مربوط به شرایط مرزی الکترومغناطیسی تغییر میکند.
معادلههای (۱۱) و (۱۲) را میتوان بر حسب شدت میدان الکتریکی نوشت. داریم:
معادله (۱۳)
یا میتوان نوشت:
معادله (۱۴)
در معادله (۱۴) فرض شده است که و محدود هستند. این معادله بیان میکند که مولفه عمودی شدت میدان الکتریکی در طول مرز مشترک ناپیوسته است.
حال معادله زیر را در نظر بگیرید:
معادله (15)
در این معادله، کل بار مغناطیسی است.
اگر بار مغناطیسی در طول مرز مشترک وجود نداشته باشد، با استفاده از فرآیند مشابه روی همین استوانه و معادله (۱۵) میتوان نوشت:
معادله (16)
یا:
معادله (17)
معادله (۱۷) بیان میکند که مولفههای عمودی چگالی شار مغناطیسی در طول مرز مشترک بین دو محیط که هیچ منبعی وجود ندارد، پیوسته هستند. معادله (۱۷) بر حسب شدت میدان مغناطیسی را میتوان به صورت زیر بازنویسی کرد:
معادله (18)
یا:
معادله (19)
معادله (۱۹) بیان میکند که مولفههای عمودی شدت میدان مغناطیسی در طول مرز مشترک، ناپیوسته هستند.
محیط با رسانایی نامحدود
اگر بار یا منابع الکتریکی حقیقی در طول مرز مشترک بین دو محیط وجود داشته باشند، یا یکی از دو محیط مرز مشترک شکل (۱)، هادی الکتریکی کامل (PEC) باشد، شرایط مرزی الکترومغناطیسی مولفههای مماسی میدان مغناطیسی در معادله (7) و مولفههای عمودی چگالی شار الکتریکی در معادله (۱۲) یا مولفههای عمودی شدت میدان الکتریکی در معادله (۱۴) باید تغییر کنند تا منابع یا بارهای الکتریکی یا چگالی جریان الکتریکی القایی () و چگالی بار الکتریکی سطحی () را شامل شود. به همین ترتیب اگر منابع و بارهای مغناطیسی در طول مرز مشترک بین دو محیط وجود داشته باشد یا یکی از دو محیط هادی مغناطیسی کامل (PMC) باشد، معادلات (۴) و (17) و (19) باید تغییر کنند.
برای رسیدن به شرایط مرزی الکترومغناطیسی مناسب در این حالتها، مجددا به شکل (۱) مراجعه کنید. فرض کنید که روی یک لایه بسیار نازک در طول مرز مشترک بار الکتریکی با چگالی سطحی به اندازه و جریان الکتریکی با چگالی خطی به اندازه وجود دارد. حال با استفاده از معادله (۵) و اعمال آن به مستطیل شکل (۱)، میتوان نوشت:
معادله (20)
در حد، ارتفاع مستطیل کوچک و کوچکتر میشود. بنابراین سمت چپ معادله (۲۰) به شکل زیر نوشته میشود:
معادله (۲۱)
از آنجا که چگالی جریان الکتریکی روی یک لایه بسیار نازک در طول مرز مشترک محدود شده است، عبارت اول سمت راست معادله (20) را میتوان به صورت زیر نوشت:
معادله (۲۲)
در حد که میل میکند، نیز صفر میشود. بنابراین عبارت آخر سمت راست معادله (20) به صورت زیر نوشته میشود:
معادله (23)
با جایگزینی معادلات (۲۱) و (۲۲) و (۲۳) در معادله (20) خواهیم داشت:
یا:
معادله (24)
از آنجا که:
معادله (25)
پس میتوان معادله (۲۴) را به شکل زیر نوشت:
معادله (26)
اتحاد برداری زیر را در نظر بگیرید:
معادله (27)
پس میتوان عبارت اول معادله (26) را به شکل زیر نوشت:
معادله (28)
یا:
معادله (29)
معادله (29) در شرایطی صحیح است که:
معادله (30)
یا:
معادله (۳۱)
اگر مستطیل در صفحات دیگر نیز وجود داشت، نتایج مشابه بود. بنابراین طبق شکل (۱)، شرایط مرزی الکترومغناطیسی برای میدان مغناطیسی مماسی به صورت زیر نوشته میشود:
معادله (32)
معادله (۳۲) بیان میکند که مولفههای مماسی میدان مغناطیسی در طول مرز مشترک، که در آن چگالی جریان الکتریکی با واحد آمپر بر متر وجود دارد، به اندازه مقدار چگالی جریان الکتریکی ناپیوسته هستند.
اگر یکی از دو محیط، هادی الکتریکی کامل (PEC) باشد، شرایط مرزی الکترومغناطیسی به دلیل حضور هادی الکتریکی کامل تغییر میکند. فرض کنید که محیط ۱ در شکل (۱) هدایت بینهایت داشته باشد (). داخل هادی کامل میدان الکتریکی وجود ندارد، پس میشود و معادله (۴) به صورت زیر نوشته میشود:
معادله (۳۳)
همچنین در داخل هادی الکتریکی کامل داریم:
معادله (۳۴)
معادله (۳۴) با این فرض به دست آمده است که محدود باشد.
به دلیل اثر پوستی، در هادی الکتریکی کامل بارهای آزاد الکتریکی، فقط در یک لایه نازک از سطح هادی وجود دارد. این بارها، چگالی سطحی بار را به وجود میآورند. این چگالی بار شامل بارهای محدود قطبیت نیست و واحد آن کولن بر متر مربع است. این نوع بار معمولا در سطح محیط دیالکتریک مشاهده میشود و دوقطبیهای اتمی را تشکیل میدهد. این دوقطبیها بارهای برابر و مخالف هم دارند و با فاصلهای بسیار کم از یکدیگر جدا شدهاند. در عوض اینجا، چگالی سطحی بار نمایانگر بارهای الکتریکی حقیقی برابر و مخالف هم است که با ابعاد محدود از یکدیگر جدا شدهاند.
هنگامی که به سطح هادی میدان الکترومغناطیسی اعمال میشود، بارهای سطحی الکتریکی تحت نیروی لورنتس میدان الکتریکی قرار میگیرند. این بارها، چگالی جریان الکتریکی با واحد آمپر بر متر را به وجود میآورند. همانند بار الکتریکی، چگالی جریان سطحی نیز روی سطح هادی باقی میماند. بنابراین مطابق شکل (۱) در حد که ، چگالی حجمی جریان الکتریکی به صورت زیر نوشته میشود:
معادله (35)
پس شرایط مرزی الکترومغناطیسی در معادله (۳۲) به صورت زیر بازنویسی میشود:
معادله (36)
معادله (36) بیان میکند که مولفه مماسی شدت میدان مغناطیسی در نزدیکی یک هادی الکتریکی کامل به اندازه چگالی خطی جریان الکتریکی القایی است.
به همی ترتیب میتوان شرایط مرزی الکترومغناطیسی را برای مولفههای عمودی شدت میدان مغناطیسی و چگالی شار الکتریکی در مرز مشترک که روی آن چگالی بار سطحی وجود دارد، نوشت. پس:
معادله (37)
در حد که ، سطح استوانهای در شکل (۲) نیز صفر میشود. بنابراین انتگرال سطحی آن نیز صفر خواهد شد. پس میتوان معادله (۳۷) را به صورت زیر نوشت:
معادله (38)
پس:
معادله (39)
معادله (۳۹) بیان میکند که مولفههای عمودی چگالی شار الکتریکی در مرز مشترک که روی آن چگالی بار سطحی وجود دارد، به مقدار چگالی بار سطحی ناپیوسته خواهند بود.
اگر معادله (۳۹) را بر حسب مولفههای عمودی شدت میدان الکتریکی، بازنویسی کنیم، خواهیم داشت:
معادله (40)
این معادله نشان میدهد که مولفههای عمودی میدان الکتریکی در مرز مشترک که روی آن چگالی بار سطحی قرار دارد، ناپیوسته هستند.
اگر یکی از دو محیط، هادی الکتریکی کامل (PEC) باشد (برای مثال محیط ۱ هدایت بینهایت داشته باشد)، معادلههای (۳۹) و (۴۰) به ترتیب به شکل زیر نوشته میشوند:
معادله (۴۱)
معادله (۴۲)
دو معادله (۴۱) و (۴۲) بیان میکنند که مولفههای عمودی چگالی شار الکتریکی و شدت میدان الکتریکی، در مجاورت هادی الکتریکی کامل با چگالی بار سطحی روی سطح هادی متناسب هستند.
منابع در طول مرز مشترک
اگر در طول مرز مشترک بین دو محیط، منابع الکتریکی و مغناطیسی (چگالی بار و جریان) وجود داشته باشد و هیچ یک از دو محیط هادی کامل نباشد، شرایط مرزی الکترومغناطیسی برای مولفههای مماسی و عمودی میدان را میتوان به صورت زیر نوشت:
معادله (43)
معادله (۴۴)
معادله (۴۵)
معادله (46)
در این روابط، () و () به ترتیب جریانهای الکتریکی و مغناطیسی و چگالی بارهای الکتریکی و مغناطیسی هستند.
جدول زیر خلاصهای از شرایط مرزی الکترومغناطیسی برای همه مولفههای میدان را نشان میدهد:
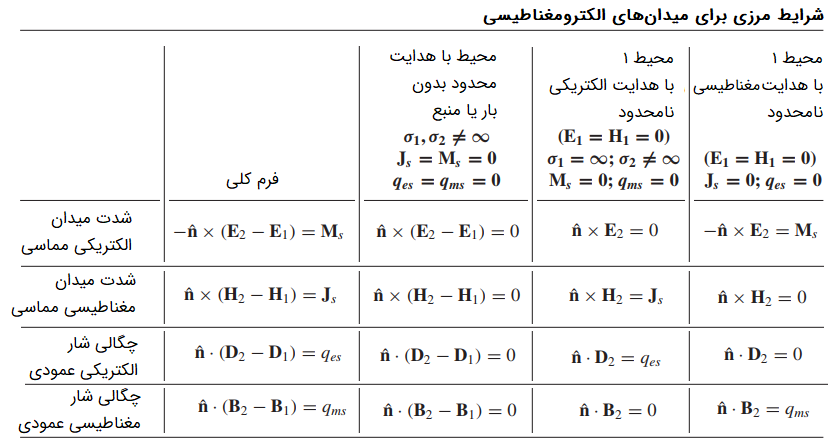
هنگامی که به یک هادی مغناطیسی کامل، میدان الکترومغناطیسی اعمال میشود، میدانهای الکتریکی و مغناطیسی متغیر با زمان در داخل هادی صفر خواهند شد. مولفههای مماسی میدان مغناطیسی نیز در نزدیکی سطح این هادی صفر میشود. به علاوه، بار مغناطیسی به سطح ماده مهاجرت میکند و یک چگالی جریان سطحی مغناطیسی روی لایهای نازک از سطح هادی ایجاد میکند. اگرچه هادی مغناطیسی کامل به صورت کلی وجود ندارد، اما دید الکترومغناطیسی مناسبی از رفتار دوگان الکتریکی آن به دست میدهد و برای حل مسائل فیزیکی مطلوب است.
جمعبندی
در حالت کلی، شرایط مرزی الکترومغناطیسی را میتوان به صورت زیر خلاصه کرد:
- مولفههای مماسی میدان الکتریکی در طول مرز مشترک، پیوسته هستند.
- مولفههای مماسی میدان مغناطیسی به اندازه چگالی سطحی جریان الکتریکی روی مرز مشترک ناپیوسته هستند.
- مولفههای عمودی چگالی شار الکتریکی به اندازه چگالی بار سطحی روی مرز مشترک ناپیوسته است.
- مولفههای عمودی میدان مغناطیسی با این فرض که بار مغناطیسی وجود ندارد، در طول مرز مشترک پیوسته هستند.
دو محیط را در مجاورت هم در نظر بگیرید که ضریب گذردهی الکتریکی و و نفوذپذیری مغناطیسی و دارند. فرض کنید که این دو محیط بدون تلف هستند یعنی:
به طور معمول، در مرز مشترک بین دو محیط بدون تلف هیچ بار آزاد الکتریکی و جریان سطحی وجود ندارد. بنابراین میتوان و را برابر صفر فرض کرد. پس شرایط مرزی الکترومغناطیسی در طول سطح مشترک این دو محیط به صورت زیر خواهد بود:
به همین ترتیب اگر محیط اول یک دیالکتریک و محیط دوم یک هادی الکتریکی کامل باشد و میدانها متغیر با زمان باشند، میتوان شرایط مرزی الکترومغناطیسی را طبق معادلاتی که بیان شد، نوشت. میدانهای الکترومغناطیسی در محیط اول یا دیالکتریک به صورت زیر هستند:
میدانهای الکترومغناطیسی در محیط دوم یا هادی الکتریکی کامل به صورت زیر نوشته میشوند:
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^












سلام
توضیحات جامع و کاملی بود
با این آموزشهای فرادرس دیگه نیازی به مطالعه کتابهای چنگ و هرینگتون و بالانیس و کالین و … وجود نداره
بنده هم به شدت به حل معادله هلم هولتز در مختصات بیضوی نیاز دارم. اگر منبعی سراغ دارید لطفا معرفی کنید
سلام و تشکر از درج مطالب درست و کامل و از همه مهم تر قابل درک و فهم برای طالب موضوع مورد نظر ، لطفا در صورت امکان کتاب یا جزوه یا منبعی که حاوی حل معادله هلم هولتز در مختصات بیضوی باشد معرفی نمایید