ساده کردن عبارت های جبری – به زبان ساده + حل تمرین و مثال
در آموزشهای پیشین مجله فرادرس با عبارت جبری و ویژگیهای آن آشنا شدیم. در این آموزش، با مفهوم ساده کردن عبارت های جبری آشنا میشویم و مثالهایی از آن را حل خواهیم کرد.
عبارت جبری چیست؟
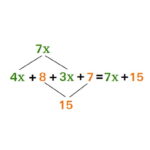
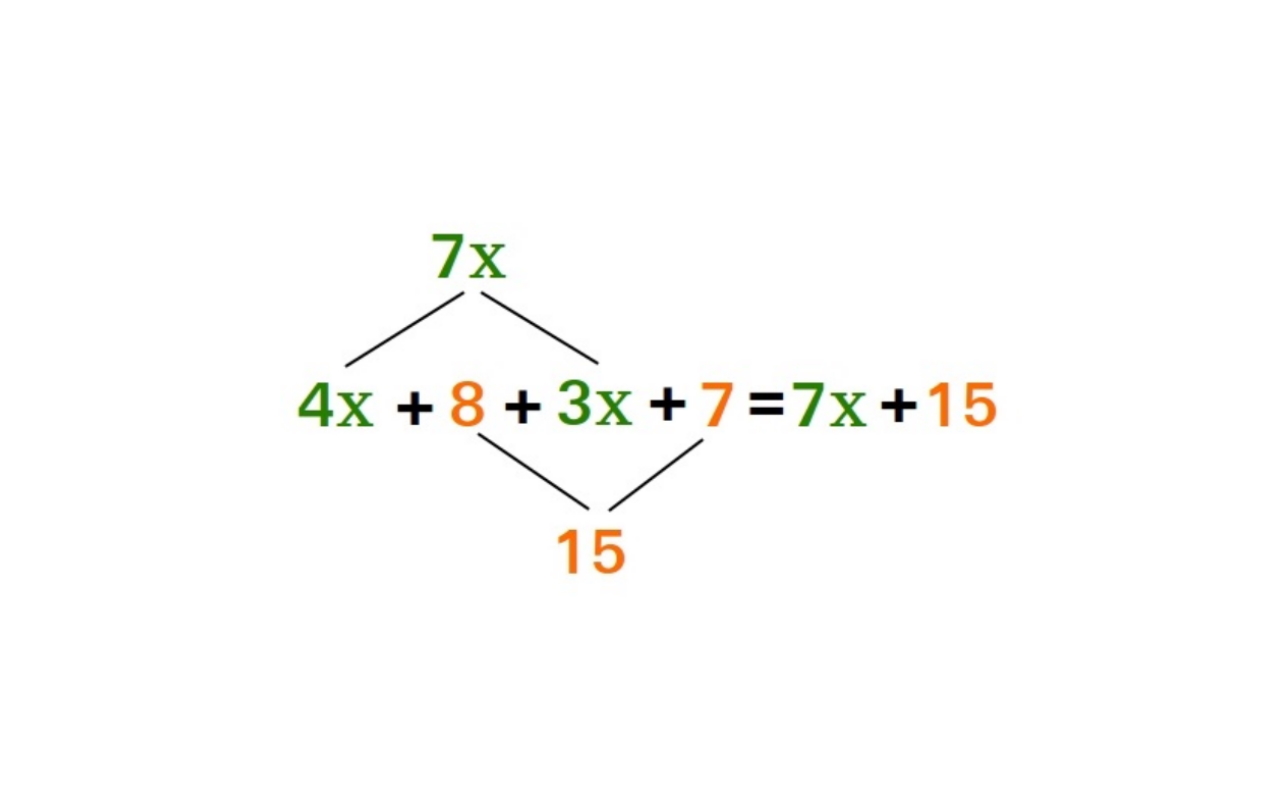
عبارت جبری (Algebraic Expression) را میتوان بهعنوان ترکیبی از جملهها (Terms) تعریف کرد که با عملیاتی مانند جمع، تفریق، ضرب، تقسیم و غیره در کنار یکدیگر قرار میگیرند. بهعنوان مثال، یک عبارت جبری است که اجزای آن در شکل زیر نشان داده شدهاند. یک عبارت جبری سه بخش دارد: متغیر، ثابت و ضریب.
در عبارت جبری، نمادی که مقدار ثابتی ندارد، متغیر (Variable) نام دارد. متغیر هر مقداری میتواند داشته باشد. از نمادهای متداولی که بهعنوان متغیر در ریاضی استفاده میشوند، میتوان به و و و و و و اشاره کرد.
همچنین، به نمادی که مقدار عددی ثابتی دارد، ثابت (Constant) میگویند. همانطور که میدانیم، همه اعداد ثابت هستند. چند مثال از ثابتها عبارتاند از و و و . یک جمله یک متغیر بهتنهایی یا یک ثابت بهتنهایی یا ترکیبی از ضرب و تقسیم متغیرها و ثابتهاست. برای مثال، و و و و امثال اینها جمله هستند. جملهها با علامت جمع یا تفریق از هم جدا میشوند. اعدادی که در متغیرها ضرب میشوند، ضریب (Coefficient) نام دارند.
ساده کردن عبارت جبری چیست؟
در بخش قبل، با مفهوم عبارت جبری آشنا شدیم. اما ساده کردن عبارت جبری چیست؟ به زبان ساده، میتوان چنین گفت که ساده کردن عبارت جبری فرایند نوشتن یک عبارت به فشردهترین و مؤثرترین شکل ممکن است، بدون آنکه تغییری در ماهیت عبارت جبری اصلی ایجاد شود.
بهعبارت دیگر، ساده کردن عبارت جبری یعنی اینکه آن را بهگونهای ساده کنیم که جملات متشابه در عبارت وجود نداشته باشند. برای سادهسازی عبارات جبری، جملات متشابه را با هم جمع یا تفریق میکنیم و اگر ضرب عبارتها وجود داشته باشد، آن را انجام میدهیم. در نهایت، پس از سادهسازی، باید یک عبارت داشته باشیم که از مجموع جملات غیرمتشابه تشکیل شده است.
در ادامه، با جملات متشابه و سایر مفاهیم مهم در ساده کردن عبارت های جبری آشنا میشویم.
مفاهیم مهم در ساده کردن عبارت های جبری
پیش از بیان روشهای ساده کردن عبارت های جبری، باید با برخی از مفاهیم مهم آشنا شویم.
جملات متشابه
در جبر، «جملههای متشابه» به جملاتی گفته میشود که پیکربندی متغیرهای آنها مشابه بوده و توانهای یکسانی نیز دارند. بهعبارت دیگر، برای آنکه دو جمله مشابه باشند، باید متغیر یا متغیرهای یکسانی داشته باشند و هر متغیر به توان مشابهی رسیده باشد.
برای مثال، و جملات مشابهی هستند، زیرا هر کدام شامل متغیر بوده و توان متغیر نیز است. اما جملات و مشابه نیستند، زیرا هر توانهای آنها با هم تفاوت دارد. بهعنوان یک مثال دیگر، و جملات مشابهی نیستند، زیرا ساختار متغیرهای دو جمله با هم یکسان نیست.
در واقع، جملات متشابه جملاتی هستند که عوامل (متغیرهای) جبری یکسانی دارند. در طرف مقابل، جملات غیرمتشابه جملاتی هستند که عوامل جبری متفاوتی دارند. برای مثال، در عبارت جبری ، جملات و جملات متشابه هستند، زیرا هر دو دارای عامل مشترک هستند. اما دو جمله و غیرمتشابه هستند، زیرا عوامل مشترکی ندارند و عوامل آنها بهترتیب و است.
فاکتورگیری
فاکتورگیری مفهومی است که براساس آن یک عدد با ضرب دو عدد دیگر بیان میشود. برای مثال، عدد را میتوان بهعنوان حاصلضرب نوشت. همین کار را میتوان برای جملات جبری نیز انجام داد. برای مثال، را میتوان بهصورت نوشت.
وقتی عبارت را بهصورت مینویسیم، در واقع از فاکتور گرفتهایم.
روش های ساده کردن عبارت های جبری
برای ساده کردن عبارت های جبری میتوان کارهای مختلفی را انجام داد که در ادامه با آنها آشنا میشویم.
جمع یا تفریق جملات متشابه
میتوانید یک عبارت جبری را با جمع یا تفریق جملات متشابه اینگونه ساده کنید:
- عبارت را طوری بازنویسی کنید که همه جملات متشابه در کنار هم باشند. هنگامی که این کار را انجام میدهید، به علامت + یا - که قبل از عبارت است، دقت کنید.
- جملات را با جمع یا تفریق عبارتهای متشابه ساده کنید.
برای مثال، میخواهیم عبارت جبری را ساده کنیم.
با توجه به آنچه که گفتیم، ابتدا بازنویسی عبارت را بهگونهای انجام میدهیم که همه جملات مشابه در کنار هم قرار گیرند: . (یا میتوانیم آن را به روشهای دیگری بنویسید، تا همه جملات کنار هم باشند و همه جملات شامل در کنار هم باشند؛ میبینیم که جمله شامل هیچ جمله مشابهی ندارد)
در ادامه، با اضافه کردن و کم کردن جملات مشابه و بازآرایی عبارت به میرسیم. با توجه به و ، عبارت سادهشده خواهد بود.
ضرب و تقسیم جملات
توجه داشته باشید که چند نوع نماد متفاوت برای نشان دادن اینکه دو (یا بیشتر) جمله باید در هم ضرب شوند وجود دارد. برای مثال، اگر قرار باشد و در هم ضرب شوند، ممکن است به صورت یا یا یا یا یا نوشته شود.
صرفنظر از نحوه نشان دادن ضرب، میتوانید یک عبارت جبری را با ضرب یا تقسیم جملات بهصورت زیر ساده کنید:
- عبارت (یا هر قسمت از عبارت، برای تقسیم) را به عنوان حاصلضرب عوامل آن بازنویسی کنید.
- در صورت لزوم، عبارت (یا هر قسمت از عبارت) را بازنویسی کنید تا همه جملات متشابه در کنار یکدیگر قرار گیرند.
- ثابت ها را ضرب/تقسیم کنید و در صورت لزوم متغیرها را ضرب/تقسیم کنید. وقتی این کار را انجام میدهید، فراموش نکنید که وقتی یک منفی در منفی ضرب (یا تقسیم) میشود، نتیجه مثبت است (به عنوان مثال ).
برای مثال، میخواهیم عبارت را ساده کنیم.
برای ساده کردن این عبارت، ابتدا عبارت را بهصورت ضرب عوامل آن بازنویسی میکنیم:
سپس، جملات مشابه را در کنار هم مینویسیم:
از آنجا که و ، عبارت بهشکل ساده میشود.
توجه داشته باشید که نمونهای از یک متغیر تواندار است (توان بهعنوان نما نیز شناخته میشود).
ضرب پرانتزها
یک عبارت یا معادله جبری اغلب دارای پرانتز یا براکت است. وقتی در یک معادله پرانتز داشته باشیم، گاهی اوقات بسط دادن آنها برای حل معادله و سادهسازی عبارت میتواند مفید باشد. در این بخش نحوه انجام این کار را توضیح میدهیم (توجه داشته باشید که مثالها به عبارات جبری اشاره دارند نه معادلات).
یک عبارت جبری متشکل از ضرب یک عبارت در یک پرانتز را میتوان به صورت زیر انجام داد:
- هر یک از ضربهایی را که باید انجام دهید، با قرار دادن عبارت خارج از پرانتز همراه با هر جمله در داخل پرانتز، بنویسید. اگر هنگام انجام این کار از نماد ضرب در قرار دادن پرانتز در اطراف هر عبارت استفاده کنید، میتوانید به سادگی هر جفت عبارت را با هم اضافه کنید و بعداً کار مربوط به علامت منفی را انجام دهید.
- هر یک از ضربهای مورد نیاز را با استفاده از روشی که قبلاً توضیح داده شد، انجام دهید و دوباره هر نتیجه را در پرانتز بگذارید تا علائم منفی را اعمال کنید. در ادامه به این موارد پرداخته خواهد شد.
- پرانتزها را از هر جمله بردارید و اگر در مجموعه پرانتزهای مربوطه وجود دارد، علامت مثبت را با علامت منفی جایگزین کنید.
مثال زیر این گامها را روشن میسازد.
میخواهیم عبارت جبری را با گسترش پرانتزها ساده کنیم.
1. ابتدا باید ضرب را انجام دهیم و را در تکتک جملات داخل پرانتز ضرب کنیم:
2. ضربها را تکتک انجام میدهیم و حاصل آنها را مینویسیم:
3. اکنون پرانتزها را حذف میکنیم و نتیجه نهایی را مینویسیم:
ضرب دو پرانتز در هم
یک عبارت جبری متشکل از دو مجموعه داخل پرانتزِ ضرب در هم را میتوان بهصورت زیر بسط داد:
- جمله اول پرانتز اول را تکتک در جملههای پرانتز دوم ضرب کنید و بین آنها علامت جمع بگذارید.
- جمله دوم پرانتز اول را تکتک در جملههای پرانتز دوم ضرب کنید و بین آنها علامت جمع بگذارید.
- برای جملههای سوم و به بعد نیز نیز همین کار را انجم دهید.
- جمله آخر پرانتز اول را تکتک در جملههای پرانتز دوم ضرب کنید و بین آنها علامت جمع بگذارید.
- جمع حاصلضربها را بنویسید.
- عبارت را با اضافه کردن و/یا کم کردن عبارات متشابه در صورت لزوم (همانطور که در بخش بالا توضیح داده شد) ساده کنید.
برای مثال، میخواهیم ضرب را انجام دهیم.
برای انجام این کار، گامهایی را که گفتیم طی و تکتک جملات را در هم ضرب میکنیم:
شکل زیر این کار را بهخوبی نشان میدهد.
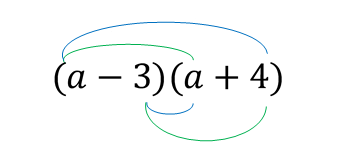
نتیجه ضربها را مینویسیم و خواهیم داشت:
پرانتزها را حذف میکنیم و خواهیم داشت:
در نهایت، جملههای متشابه را در کنار هم نوشته و ساده میکنیم و عبارت ساده نهایی را بهدست میآوریم:
بهعنوان یک مثال دیگر، فرض کنید میخواهیم عبارت را ساده کنیم. برای این کار، مینویسیم:
اتحادهای جبری
یکی از مهمترین ابزارهایی که میتوانند ما را در ساده کردن عبارتهای جبری کمک کنند، اتحادهای جبری هستند. اتحادها فرمولهای معادل ضرب پرانتزها را به ما میدهند و دیگر نیاز نیست ضربهای زمانبر را انجام دهیم.
مهمترین اتحادهایی که از آنها در ساده کردن عبارت های جبری استفاده میشود، به عبارتند از:
- اتحاد مربع دوجملهای:
- اتحاد مربع سهجملهای:
- اتحاد بسط دوجملهای نیوتن:
- اتحاد لاگرانژ:
- اتحاد اویلر:
مثالهای ساده کردن عبارت های جبری
در این بخش، مثالهایی را از ساده کردن عبارتهای جبری بیان میکنیم.
مثال اول ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: کافی است عدد پشت پرانتز را در پرانتز ضرب کنیم:
مثال دوم ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: با ضرب جمله در پرانتز، خواهیم داشت:
مثال سوم ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: با ضرب دو پرانتز در هم، خواهیم داشت:
مثال چهارم ساده کردن عبارت های جبری
عبارت را ساده کنید.
حل: برای سادهسازی این عبارت، دو پرانتز را در هم ضرب کرده، سپس جملات متشابه را با هم ساده میکنیم:
مثال پنجم ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: این عبارت بهصورت زیر ساده میشود:
مثال ششم ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: این عبارت اینگونه ساده میشود:
مثال هفتم ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: این عبارت بهصورت زیر ساده میشود:
مثال هشتم ساده کردن عبارت های جبری
عبارت را ساده کنید.
حل: عبارت پشت پرانتز را در عبارت داخل پرانتز ضرب میکنیم و داریم:
مثال نهم ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: دو پرانتز را در هم ضرب کرده و جملات متشابه را با هم ساده میکنیم:
مثال دهم ساده کردن عبارت های جبری
عبارت را ساده کنید.
حل: با ضرب پرانتزها در هم، خواهیم داشت:
مثال یازدهم ساده کردن عبارت های جبری
عبارت را ساده کنید.
حل: این عبارت بهصورت زیر ساده میشود:
مثال دوازدهم ساده کردن عبارت های جبری
عبارت را سادع کنید.
حل: برای سادهسازی این عبارت، کافی است جملههای پرانتزها را در هم ضرب کنیم:
یک راه سادهتر برای ساده کردن این عبارت، استفاده از اتحاد جمله مشترک است.
مثال سیزدهم ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: گامهای زیر را طی میکنیم:
1. عبارت را بهصورت زیر بازنویسی میکنیم:
2. جملات مشابه از قبل در کنار یکدیگر قرار دارند، بنابراین نیازی به بازنویسی نیست.
3. از آنجا که و و ، عبارت در نهایت بهشکل ساده میشود.
توجه داشته باشید که تقسیم فوق با ساده کردن کسرها انجام شده است و برای متغیرها به همان روشی عمل میکنیم که برای ثابتها.
مثال چهاردهم ساده کردن عبارت های جبری
عبارت جبری زیر را ساده کنید:
حل: در سه گام ساده این کار را انجام میدهیم.
1. ابتدا میتوانیم عبارت را اینگونه بنویسیم:
۲. در گام بعدی، عبارتهای درون پرانتزها را بیرون میآوریم و جایی که علامت پشت پرانز منفی است، جملههای داخل آن را قرینه میکنیم:
۳. جملههای متشابه را ساده میکنیم و خواهیم داشت:
مثال پانزدهم ساده کردن عبارت های جبری
عبارت جبری زیر را ساده کنید.
حل: طبق آنچه گفتیم، این عبارت بهصورت زیر ساده میشود:
مثال شانزدهم ساده کردن عبارت های جبری
عبارت جبری را ساده کنید.
حل: ابتدا به صورت و مخرج نگاهی میاندازیم. صورت را سعی میکنیم تجزیه کنیم. به سراغ اتحاد جمله مشترک میرویم. باید دو عدد پیدا کنیم که جمعشان برابر با و ضربشان برابر با شود. این دو عدد و هستند. بنابراین، میتوان صورت کسر را اینگونه نوشت:
بهطور مشابه، برای مخرج کسر، داریم:
بنابراین، میتوان نوشت:
مثال هفدهم ساده کردن عبارت های جبری
پس از بررسی مثالهای بالا، عبارات جبری زیر را ساده کردهایم. سعی کنید خودتان از ابتدا راه راه ساده کردن را بپیمایید:
معرفی فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی
یکی از آموزشهای ویدیویی دوره دبیرستان فرادرس، «آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی» است که به طور ویژه مربوط به دانشآموزان رشته علوم انسانی است. این آموزش ویدیویی در قالب چهار درس و در زمان ۶ ساعت و ۱۹ دقیقه تدوین شده است. در درس یکم، معادله درجه دوم مورد بحث قرار گرفته که شامل مطالب اصلی درس، نکات مهم و مثالهای حل شده است. در درس دوم، موضوع مهم تابع ارائه شده و در آن، به موارد مهمی از قبیل تعریف ضابطه و تابع، رسم آن، دامنه و برد تابع و... پرداخته شده است. کار با دادههای آماری موضوع درس سوم است. در نهایت، در درس چهارم به طور کامل، مطالب کتاب درسی درباره نمایش دادهها ارائه شده است.
- برای مشاهده فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی + اینجا کلیک کنید.
معرفی فیلم آموزش ریاضی پایه دانشگاهی
یکی از آموزشهایی که برای آشنایی بیشتر با مبحث اتحاد و تجزیه میتوانید به آن مراجعه کنید، آموزش ریاضی پایه دانشگاهی است. این آموزش که مدت آن ۱۲ ساعت و ۴۶ دقیقه است، در قالب ۱۰ درس تهیه شده است.
در درس اول، مجموعهها، مجموعه اعداد، توان، ب.م.م و ک.م.م معرفی شدهاند. موضوعات درس دوم، چندجملهایها و اتحاد و تجزیه است. در درس سوم، نامساویها، نامعادلات، طول پارهخط، ضریب زاویه و معادله خط مورد بحث قرار گرفتهاند. مثلثات موضوع مهم درس چهارم است. تصاعد حسابی و هندسی در درس پنجم بررسی شدهاند. تابع و دامنه و برد آن موضوعات مهم درس ششم هستند. در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع ارائه شدهاند. در درس هشتم به توابع زوج و فرد، تابع یک به یک و تابع وارون پرداخته شده است. انواع توابع از قبیل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح موضوع درس نهم هستند. در نهایت، در درس دهم توابع نمایی و لگاریتمی مورد بحث قرار گرفتهاند.
- برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.
جمعبندی
در این آموزش، عبارت جبری و اجزای آن را بهطور اجمالی معرفی کردیم. همچنین، با روشهای ساده کردن عبارتهای جبری آشنا شدیم و مثالهای متنوعی را حل کردیم.
آزمون ساده کردن عبارتهای جبری
۱. کدام مورد تعریف صحیحی از عبارت جبری ارائه میدهد؟
ترکیبی از عددهای ثابت بدون استفاده از متغیرها تشکیل شده است.
فقط شامل متغیرها و بدون هیچ عددی نوشته میشود.
ترکیبی از جملههاست که با عملگرهای ریاضی مانند جمع، تفریق، ضرب و تقسیم به هم پیوستهاند.
شامل عبارتهایی است که فقط ضرب و تقسیم را به کار میبرند.
عبارت جبری به ترکیبی از جملهها گفته میشود که با عملگرهای ریاضی مثل جمع، تفریق، ضرب و تقسیم به هم پیوستهاند.
۲. در عبارت جبری 5x + 2y − 7، اجزای ضریب، متغیر و ثابت کدامند؟
ضریب: 7، متغیر: 5x و 2y، ثابت: x
ضریب: 5 و 2، متغیر: 7، ثابت: x و y
ضریب: x و y، متغیر: 5 و 2، ثابت: 7
ضریب: 5 و 2، متغیر: x و y، ثابت: 7-
در عبارت جبری، عددهایی که کنار متغیرها هستند ضریب نام دارند و در اینجا 5 و 2 هستند. x و y نقش متغیر را دارند و 7- هم عددی بدون متغیر است که ثابت است.
۳. کدام مورد اجزای اصلی عبارت جبری را تشکیل میدهد؟
متغیر، ثابت و ضریب
نماد، جمع و تقسیم
عدد صحیح، کسر و نماد
پرانتز، توان و جذر
در ساختار عبارت جبری، بهطور مشخص سه جزء اصلی وجود دارد: «متغیر» (variable)، «ثابت» (constant) و «ضریب» (coefficient).
۴. در عبارت جبری ، کدام مورد درباره تشخیص متغیر، ضریب و ثابت صحیح است؟
متغیر x، ضرایب ۱ و ۳، ثابت صفر
متغیر x، ضرایب ۱ و ۳، ثابت ۳
متغیر x، ضرایب ۱ و ۳، ثابت منفی ۴
متغیر x، ضرایب ۱ و ۳، ثابت ۴
در عبارت ، متغیر همان x است، ضریب جمله اول ۱ و ضریب جمله دوم ۳ در نظر گرفته میشود و عدد منفی ۴ عددی است که کنار هیچ متغیری قرار ندارد، پس ثابت نام دارد.
۵. تفاوت اصلی جملات متشابه و غیرمتشابه در عبارات جبری چیست؟
جملات غیرمتشابه همیشه بدون علامت هستند.
جملات غیرمتشابه فقط شامل ضرایب مختلفاند.
جملات متشابه تعداد متغیرهای بیشتری دارند.
جملات متشابه دارای ساختار متغیر و توان یکسان هستند.
جملات متشابه در عبارات جبری آنهایی هستند که ساختار متغیرها و توانها در آنها یکسان است، یعنی متغیر و مقدار توان در هر دو جمله مانند هم باشد..
۶. هدف اصلی سادهسازی یک عبارت جبری در ریاضیات پایه چیست؟
افزایش تعداد جملات موجود در عبارت
رسیدن به عبارتی با جملات غیرمتشابه و کوتاهتر
تبدیل همه متغیرها به اعداد
تغییر معنی و مقدار عبارت جبری
منظور از سادهسازی عبارت جبری این است که آن را به صورتی فشرده و موثر بازنویسی کنیم که فقط جملات غیرمتشابه باقی بماند و تعداد جملات تکراری یا مشابه حذف شود. سادهسازی به معنای تبدیل متغیرها به اعداد یا افزایش تعداد جملات نیست و نباید معنی یا مقدار اصلی عبارت تغییر کند. بنابراین، رسیدن به بیان کوتاه و بدون جملات تکراری هدف نهایی این کار است.
۷. دلیل اینکه فقط جملات متشابه در سادهسازی عبارت جبری با هم جمع یا تفریق میشوند چیست؟
به دلیل اینکه ضریبهای ثابت فقط روی جملات متفاوت تاثیر میگذارند.
زیرا جملات متشابه ساختار متغیر یکسان دارند و ترکیبشان ماهیت را تغییر نمیدهد.
چراکه تنها جملات نامتشابه به صورت مستقیم قابل جمع هستند.
چون فقط جملات نامتشابه قابل ضرب با یکدیگر هستند و جمع امکانپذیر نیست.
در سادهسازی عبارت جبری، تنها جملات متشابه یعنی آنهایی که دقیقا متغیر و توان یکسان دارند، قابل جمع یا تفریق هستند.
۸. در سادهسازی عبارات جبری، در چه وضعیتی کاربرد جمع یا تفریق جملههای موجود باعث تغییر در ساختار عبارت نمیشود و عبارت همچنان به شکل ابتدایی باقی میماند؟
هنگامی که فقط یک متغیر در تمام جملهها وجود داشته باشد.
زمانی که جملههای موجود متشابه نباشند.
هنگامی که جملهها دارای عدد ثابت باشند.
زمانی که همه ضرایب جملهها یکسان باشند.
اگر جملههای موجود در یک عبارت جبری متشابه نباشند (یعنی ساختار متغیرها و توانهای آنها یکسان نباشد)، جمع یا تفریق آنها ممکن نیست و عبارت سادهتر نمیشود و به همان شکل اولیه باقی میماند.
۹. برای سادهسازی عبارتی که هم جمله متشابه دارد و هم جمله غیرمتشابه، چه روندی باید طی شود؟
تمام جملات با هم جمع میشوند و عبارت کوتاه میشود.
جملات غیرمتشابه حذف میشوند تا فقط متشابه باقی بماند.
همه ضرایب برابر یک قرار میگیرند تا عبارت ساده شود.
ابتدا جملات متشابه با هم جمع یا تفریق میشوند و سپس فقط جملات غیرمتشابه باقی میماند.
در این فرآیند، ابتدا باید جملات متشابه را با هم جمع یا تفریق کرد تا تکراریها حذف شوند و هر متغیر فقط یک بار با حاصلجمع ضرایب ظاهر شود. پس از پایان این مرحله، جملات غیرمتشابه دستنخورده باقی میمانند و چون ساختار متفاوتی دارند ترکیب نمیشوند.
۱۰. در زمان گسترش پرانتزها در عبارات جبری، کدام نکته مهم باید رعایت شود تا نتیجه صحیح باشد؟
تمام جملات داخل هر پرانتز باید با هم جمع شوند.
ضرایب جملات هنگام گسترش حذف شوند.
پرانتزها باید فقط زمانی باز شوند که جملات متشابه باشند.
هر جمله از پرانتز اول باید در هر جمله پرانتز دوم ضرب شود.
برای گسترش صحیح پرانتزها در عبارات جبری، لازم است هر جمله از پرانتز اول در هر جمله پرانتز دوم ضرب شود تا حاصل کامل و درست به دست آید. جمع کردن جملات داخل یک پرانتز، روش سادهسازی نیست و ممکن است اشتباه باشد. حذف ضرایب، نادرست است چون ضرایب نقش کلیدی در مقدار عبارت دارند. باز کردن پرانتزها فقط هنگام وجود جملات متشابه نیز صحیح نیست.
۱۱. استفاده از اتحاد مربع دو جملهای بیشتر برای ساده کردن کدام یک از عبارات زیر مناسب است؟
عبارتهایی با جمع دو جمله مشابه و بدون توان
عبارتهایی با ضرب دو پرانتز متفاوت
عبارتهایی به شکل جمع یا تفریق دو جمله همراه با توان دو
عبارتهایی با ضرب جمله و پرانتز بدون توان
استفاده از اتحاد مربع دو جملهای برای عباراتی مناسب است که دو جمله با توان دو به صورت جمع یا تفریق دارند، مانند . فقط در این ساختار میتوان با استفاده از اتحاد، عبارت را به صورت فشردهتر بازنویسی کرد.
۱۲. اگر ضرایب دو جمله با متغیرهای یکسان متفاوت باشند، این جملهها از چه نوعی هستند و چه اثری بر روند ساده کردن دارند؟
این جملهها متشابه هستند و در سادهسازی باید با هم جمع یا تفریق شوند.
این جملهها باید فاکتورگیری شوند تا ساده شوند.
این جملهها را میتوان مستقیما تقسیم کرد تا سادهسازی انجام شود.
این جملهها غیرمتشابه هستند و نمیتوان آنها را با هم ترکیب کرد.
زمانی که ضرایب جملات متفاوت باشد اما متغیر و توان یکسان نداشته باشند، این دو جمله غیرمتشابه تلقی میشوند. در سادهسازی، جملات غیرمتشابه قابل جمع یا تفریق با یکدیگر نیستند و هر کدام باید به شکل جداگانه در عبارت باقی بماند. برخلاف جملات متشابه که قابل ترکیب هستند، جملات غیرمتشابه فقط در پاسخ نهایی ساده نشده حضور دارند.
۱۳. برای ساده کردن کسرهای جبری، کدام روشهای زیر معمولا به کار میروند و نقش اصلی آنها چیست؟
گسترش حاصلضرب پرانتزها برای سادهسازی توانها
جمع و تفریق برای تجمیع جملات متشابه و ساماندهی صورت و مخرج
استفاده از اتحادها فقط برای جمع جملات متشابه
فاکتورگیری برای تجزیه صورت و مخرج و حذف عوامل مشترک
در ساده کردن کسرهای جبری، معمولا فاکتورگیری به کار میرود تا بتوان صورت و مخرج را به عوامل سادهتر تجزیه و عوامل مشترک را حذف کرد.


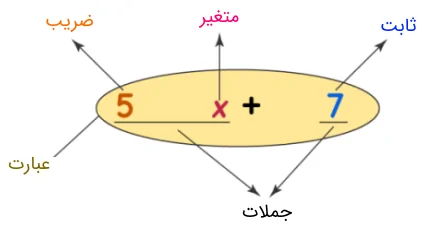











5⁴×3⁴عبارت زیر را ساده کنید
چون پایه ها متفاوتن ولی توان ها یکین ، یکی از توان ها رو مینویسیم و بعد عملیات ضرب رو انجام میدیم . 15⁴=5⁴×3⁴