خواص دترمینان — به زبان ساده

در آموزش‌های پیشین مجله فرادرس، با دترمینان و همچنین روش‌های محاسبه دترمینان ماتریس‌های ۳ در ۳ آشنا شدیم. در این آموزش، برخی از مهم‌ترین خواص دترمینان را معرفی می‌کنیم.

۱. دترمینان ماتریس مربعی $$\left[ {{a_{ij}}} \right]$$‌ با اندازه $$n$$، یک چندجمله‌ای متشکل از درایه‌های این ماتریس شامل $$n !$$ جمله به فرم $${ \left ( { – 1 } \right ) ^ s } { a _ { 1 { k _ 1 } } } { a _ { 2 { k _ 2 } } } \cdots { a _ { n { k _ n } } }$$ است. هر یک از این جملات متناظر با یکی از $$n!$$ ترتیب $$k_ 2$$، ... و $$k _ n$$ از $$s$$ از زوج جایگشت‌های عناصر مجموعه $$1$$، $$2$$، ... و $$n$$ است. مقدار دترمینان با ترکیب‌های خطی از سطرها یا ستون‌ها یا ترانهاده ماتریس تغییری نمی‌کند.

۲. دترمینان یک ماتریس مرتبه $$n$$ به صورت زیر نوشته می‌شود:

$$ \large \det A = \left | { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 11 } } } & { { a _ { 1 2 } } } & \ldots & { { a _ { 1j } } } & \ldots & { { a _ { 1 n } } } \\<br /> { { a _ { 2 1 } } } & { { a _ { 2 2 } } } & \ldots & { { a _ {2 j } } } & \ldots & { { a _ { 2n } } } \\<br /> \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\<br /> { { a _ { i 1 } } } & { { a _ { i 2 } } } & \ldots & { { a _ { ij } } } & \ldots & { { a _ { i n } } } \\<br /> \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\<br /> { { a _ { n 1 } } } & { { a _ { n 2 } } } & \ldots & { { a _ { n j } } } & \ldots & { { a _ { n n } } }<br /> \end {array} } \right | $$

۳. دترمینان ماتریس مرتبه دوم شامل دو جمله است که هریک از آن‌ها شامل ضرب دو درایه ماتریس هستند:

$$ \large \det A = \left | { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } } } & { { a _ { 1 2 } } } \\<br /> { { a _ { 2 1 } } } & { { a _ { 2 2 } } }<br /> \end {array} } \right | = { a _ { 1 1 } } { a _ { 2 2 } } – { a _ { 1 2 } } { a _ { 2 1 } } $$

۴. دترمینان ماتریس مرتبه سوم شامل ۶ جمله است که هریک از آن‌ها شامل ضرب سه درایه ماتریس هستند:

$$ \large \begin {align*} \det A = \left | { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } } } & { { a _ { 1 2 } } } & { { a _ { 1 3} } } \\<br /> { { a _ { 2 1 } }} & { { a _ { 2 2 } } } & { { a _ { 2 3 } } } \\<br /> { { a _ { 3 1 } } } & { { a _ {3 2 } } } & { { a _ { 3 3 } }}<br /> \end {array} } \right | & = { a _ { 1 1 } } { a _ { 2 2 } } { a _ { 3 3 } } + \; { a _ { 1 2 } } { a _ { 2 3 } } { a _ { 3 1 } } + \; { a _ { 1 3 } } { a _ { 2 1 } } { a _ { 3 2 } } \\ & \;\;\;\;\; - \; { a _ { 1 1 } } { a _ {2 3 } } { a _ { 32 } } - \; { a _ { 1 2 } }{ a _ { 2 1 } } { a _ { 3 3 } } - \; { a _ { 1 3 } } { a _ { 2 2 } } { a _ { 3 1 } } \end {align*} $$

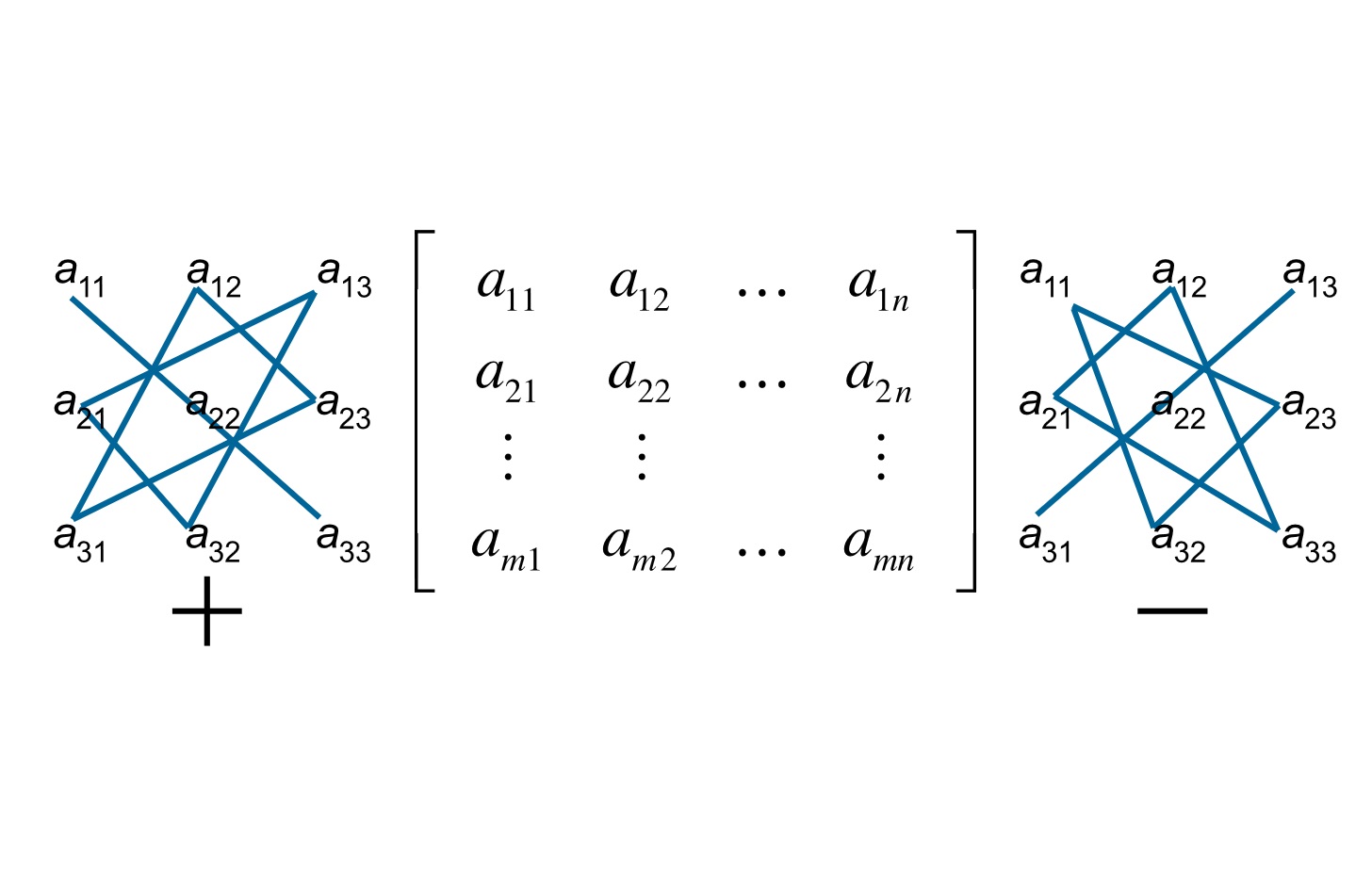
۵. دترمینان ماتریس مرتبه سوم را می‌توان با استفاده از روش ساروس نیز محاسبه کرد. سه تا از شش جمله با علامت مثبت درج شده و سه جمله دیگر با علامت منفی در نظر گرفته می‌شوند. درایه‌های سه‌تایی با هم به صورت شماتیک در شکل نشان داده شده‌اند.

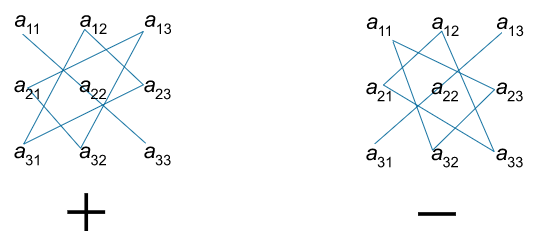
۶. کهاد $$M _ { i j }$$ متناظر با درایه $$a _ { i j }$$ از ماتریس مرتبه $$n$$اُم $$A$$، دترمینان مرتبه $$(n - 1 )$$ به دست آمده از ماتریس $$A$$ با حذف سطر $$i$$اُم و ستون $$j$$اُم است.

7. الحاقی $$A _ { i j }$$ کهاد $$M _ { i j }$$ ضرب در $$- 1$$ به توان $$( i + j )$$ است:

$$\large { A _ { i j } } = { \left ( { – 1 } \right ) ^ { i + j } } { M _ { i j } }$$

۸. دترمینان مرتبه $$n$$ را می‌توان با استفاده از فرمول لاپلاس نیز محاسبه کرد. در این صورت، با گسترش دترمینان در سطر $$i$$اُم، فرمول آن به صورت زیر است:

$$\large \det A = \sum \limits _ { j = 1 } ^ n { { a _ { i j } }{ A _ { i j } } } , \; i = 1 , 2 , \ldots , n$$

هنچنین، با گسترش دترمینان در ستون $$j$$اُم، خواهیم داشت:

$$\large \det A = \sum \limits _ { i = 1 } ^ n { { a _ { i j } } { A _ { i j } } } , \; \; j = 1 , 2 , \ldots , n$$

۹. دترمینان ترانهاده یک ماتریس مربعی برابر با دترمینان ماتریس اصلی است:

$$ \large \left | { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } } & { { a _ 2 } } \\<br /> { { b _ 1 } } & { { b _ 2 } }<br /> \end {array} } \right | = \left | { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } } & { { b _ 1 } } \\<br /> { { a _ 2 } } & { { b_ 2 } }<br /> \end {array} } \right | $$

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

۱۰. اگر جای دو سطر یا ستون را تعویض کنیم، علامت دترمینان تغییر می‌کند:

$$ \large \left | { \begin {array} { * { 2 0 } {c } }<br /> { { a _ 1 } } & { { b _ 1 } } \\<br /> { { a _ 2 } } & { { b _ 2 } }<br /> \end {array} } \right | = - \left | { \begin {array} { * { 20 } { c } }<br /> { { a _ 2 } } & { { b _ 2 } } \\<br /> { { a _ 1 } } & { { b _ 1 } }<br /> \end {array}} \right |$$

۱۱. اگر یک ماتریس دو سطر یا ستون برابر داشته باشد، دترمینان آن صفر خواهد بود:

$$ \large \left | { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } } & { { a _ 1 } } \\<br /> { { a _ 2 } } & { { a _ 2 } }<br /> \end {array} } \right | = 0 $$

۱۲. ضرب درایه‌های یک سطر (یا ستون) در یک عدد، معادل با ضرب دترمینان در آن عدد است. به عبارت دیگر، یک عامل ثابت از درایه‌های هر سطر (یا ستون) را می‌توان از دترمینان بیرون آورد:

$$ \large \left | { \begin {array} { * { 2 0 } { c } }<br /> { k { a _ 1 } } & { k {b _ 1 } } \\<br /> { { a _ 2 }} & { { b _ 2 } }<br /> \end {array} } \right | = k \left | { \begin {array} { * { 2 0 } {c } }<br /> { { a _ 1 } } & { { b _ 1 } } \\<br /> { { a _ 2 } } & { { b _ 2 } }<br /> \end {array} } \right | $$

13. اگر درایه‌های هر سطر (یا ستون) در یک عدد ثابت ضرب شده و با درایه‌های متناظر سطر (یا ستون) دیگر جمع شوند، آنگاه مقدار دترمینان تغییری نخواهد کرد:

$$ \large \left | { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } + k { b _ 1 } } & { { b _ 1 } } \\<br /> { { a _ 2 } + k { b _ 2 } } & { { b _ 2 } }<br /> \end {array} } \right | = \left | { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } } & { { b _ 1 } } \\<br /> { { a _ 2 } } & { { b _ 2 } }<br /> \end {array} } \right | $$

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش جبر خطی با متلب
• مجموعه آموزش‌های مهندسی کنترل
• آموزش کنترل مدرن به همراه پیاده سازی در متلب​‎
• تجزیه مقادیر منفرد (SVD) — به زبان ساده
• خواص ماتریس ها — به زبان ساده
• تقلب نامه (Cheat Sheet) جبر خطی برای یادگیری ماشین — راهنمای سریع و کامل

^^