جمع و تفریق اعداد مرکب – به زبان ساده + حل تمرین

در آموزش‌های پیشین مجله فرادرس، با اعداد مخلوط و جمع و تفریق آن‌ها آشنا شدیم. در این آموزش از مجموعه آموزش‌های ریاضی مجله فرادرس، با جمع و تفریق اعداد مرکب آشنا می‌شویم.

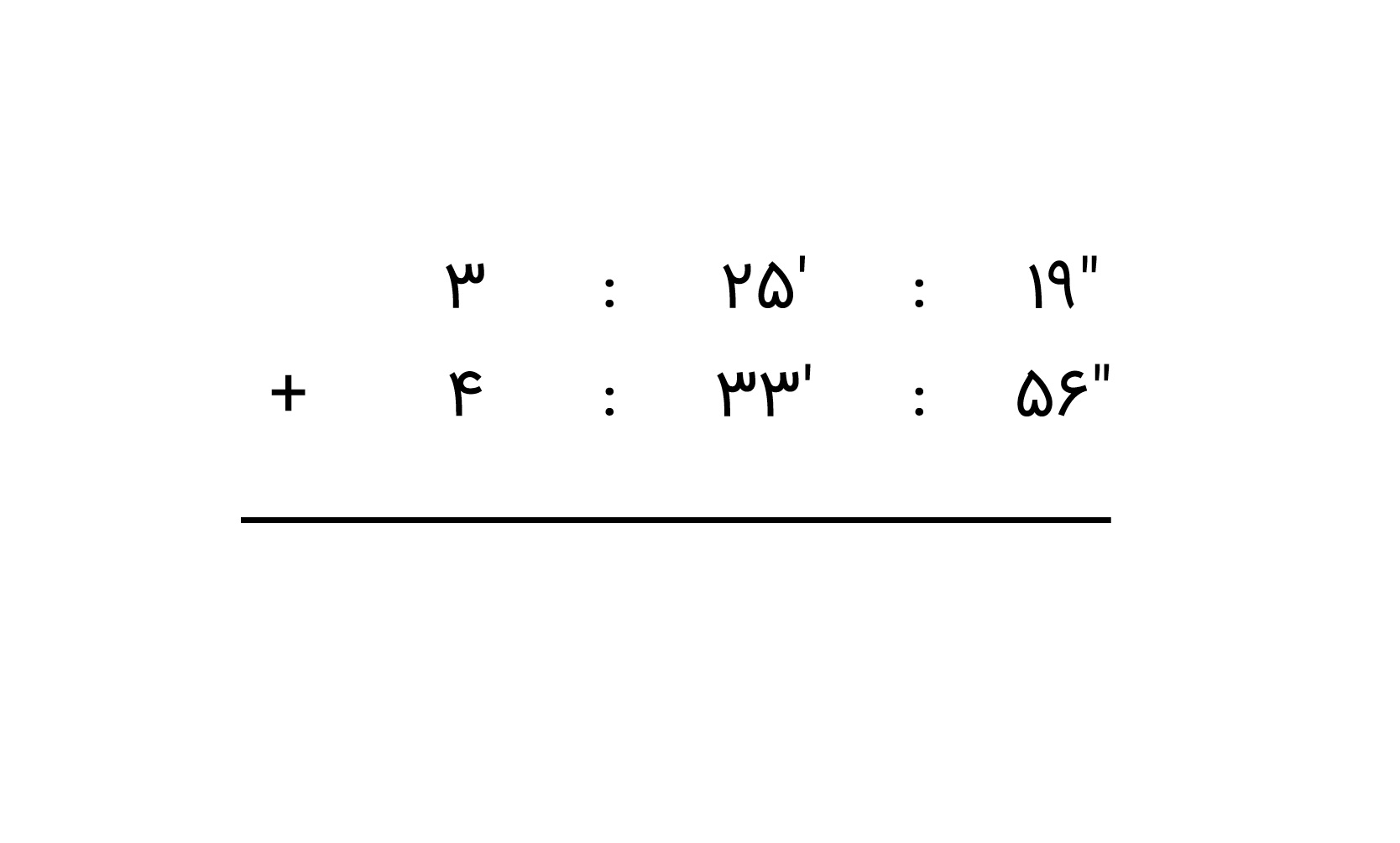
قبل از اینکه به آموزش جمع و تفریق اعداد مرکب را آغاز کنیم، باید بدانیم که عدد مرکب در ریاضیات به دو نوع عدد گفته می‌شود و باید بین آن‌ها تفکیک قائل شویم. در ادامه، این اعداد را معرفی می‌کنیم.

عدد مرکب (اعداد طبیعی مقابل اعداد اول)

همان‌طور که در آموزش‌ «اعداد اول — به زبان ساده (+ دانلود فیلم آموزش رایگان)» دیدیم، عدد اول عددی است که تنها بر خودش و یک بخش‌پذیر است. عدد مرکب (Composite Number) در مقابل عدد اول قرار می‌گیرد. در نظریه اعداد، عدد مرکب عددی است که می‌توان آن را به‌صورت ضرب دو عدد طبیعی کوچک‌تر خودِ آن عدد و بزرگ‌تر از یک نوشت. برای مثال، اعداد زیر را در نظر بگیرید:

$$8, 9, 11, 17, 23, 24$$

سعی می‌کنیم این اعداد را به‌صورت حاصل‌ضرب شمارنده‌هایشان (عواملشان) بنویسیم:

$$\large \begin {align} 8 & : 1 , 2 , 4 , 8 \\ 9 & : 1 , 3 , 9 \\ 11 & : 14 , 11 \\ 17 & : 1 , 17 \\ 23 & : 1 , 23 \\ 24 & : 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24 \end {align}$$

همان‌طور که می‌بینیم، اعداد اولِ $$11$$ و $$17$$ و $$23$$ تنها بر دو عدد (خودشان و یک) بخش‌پذیرند. اما اعداد مرکبِ $$8$$ و $$9$$ و $$2 4$$ بر بیش از دو عدد بخش‌پذیرند.

به‌عنوان یک مثال، می‌خواهیم شمارنده‌های عدد $$28$$ را بررسی کنیم. می‌دانیم که برای بررسی شمارنده‌های یک عدد، کافی است اعداد کوچک‌تر از نصف آن را بررسی کنیم. نصف عدد $$28$$ می‌شود $$14$$. عدد $$28$$ بر $$2$$ بخش‌پذیر است، بنابراین، $$2$$ شمارنده آن است. بنابراین، $$14$$ نیز شمارنده آن است. عدد $$28$$ بر $$3$$ بخش‌پذیر نیست، زیرا مجموع رقم‌هایش $$2 + 8=10$$ است که بر $$3$$ بخش‌پذیر نیست. عدد $$4$$ و $$7$$ نیز شمارنده $$28$$ هستند. عدد $$5$$ شمارنده $$28$$ نیست. اگر از ماشین‌حساب استفاده کنیم، می‌بینیم که اعداد $$8$$ و $$9$$ و $$10$$ و $$11$$ و $$12$$ و $$13$$ نیز شمارنده $$28$$ نیستند. بنابراین، شمارنده‌های عدد $$28$$‌به‌‌صورت زیر هستند و این عدد یک عدد مرکب است:

$$\large \begin {align} 28 & : 1 , 2 , 4 , 7 , 14 , 28 \end {align}$$

برای آشنایی بیشتر با این نوع از اعداد مرکب، به آموزش‌های زیر مراجعه کنید:

• اعداد مرکب چیست و چه اعدادی هستند؟ | به زبان ساده و با مثال
• عدد مرکب چیست ؟ — خواص عدد — به زبان ساده

جمع و تفریق اعداد مرکب (در مقابل اعداد اول)

همان‌طور که دیدیم، اعداد مرکب، دسته‌ای از اعداد طبیعی هستند و جمع و تفریق آن‌ها نیز به‌سادگی مانند همه اعداد طبیعی دیگر انجام می‌شود. معمولاً‌ اعداد طبیعی را به سه دسته اعداد اول، اعداد مرکب و عدد استثنا تقسیم می‌کنند. عدد استثنا همان عدد یک است.

برای مثال، دو عدد مرکب $$28$$ و $$6$$ را در نظر بگیرید. جمع و تفریق این دو عدد به‌سادگی به‌صورت زیر انجام می‌شود.

$$\large \begin {align} 28 + 6 & = 34 \\ 2 8 - 6 & = 22 \end {align}$$

آنچه بیشتر در مورد جمع و تفریق اعداد مرکب بیان می‌شود، مربوط به اعداد مرکب دیگری است که در ادامه با آن‌ها آشنا می‌شویم.

اعداد مرکب (اعدادی با واحدهای متفاوت)

به زبان ساده، این نوع اعداد مرکب اعدادی هستند که از چند واحد تشکیل شده‌اند. برای مثال، وقتی می‌گوییم ۲ ساعت و ۴۵ دقیقه، یعنی با یک عدد مرکب مواجه هستیم که هم واحد ساعت دارد و هم واحد دقیقه. یا وقتی که می‌گوییم جرم میوه ۱ کیلوگرم و ۲۰۰ گرم است یا وقتی می‌گوییم طول اتاق ۳ متر و ۳۵ سانتی‌متر است، از اعداد مرکب استفاده کرده‌ایم.

اعداد مرکب معمولاً به موارد زیر مربوط هستند:

• زمان
• جرم
• طول

البته موارد دیگری نیز وجود دارند که از واحدهای عدد مرکب برای آن‌ها استفاده می‌شود، اما رایج‌ترین موارد سه موردی هستند که بیان شد.

اعداد مرکب مربوط به زمان

واحدهای مختلفی برای زمان وجود دارد که احتمالاً آن‌ها را شنیده‌اید:

• سال: هر سال ۱۲ ماه است.
• ماه: همان‌طور که می‌دانیم، ۱۲ ماه داریم که می‌توان آن‌ها را به شش ماه اول سال و شش ماه دوم سال تفسیم کرد. این تقسیم‌بندی به این علت است که شش ماه اول سال ۳۱ روز دارند و شش ماه دوم سال ۳۰ روز.
  • شش ماه اول سال که فروردین، اردیبهشت، خرداد، تیر، مرداد، شهریور هستند، ۳۱ روز دارند.
  • شش ماه دوم سال که مهر، آبان، آذر، دی، بهمن، اسفند هستند، ۳۰ روز دارند.
  • نکته: ماه اسفند هر چهار سال یک‌بار ۳۰ روزه است که به آن سال سال کبیسه می‌گوییم.
  • ماه‌ها را این‌گونه با اعداد نشان می‌دهیم: ماه اول یا ۱ (فروردین)، ماه دوم یا ۲ (اردیبهشت)، ماه سوم یا ۳ (خرداد)، ماه چهارم یا ۴ (تیر)، ماه پنجم یا ۵ (مرداد)، ماه ششم یا ۶ (شهریور)، ماه هفتم یا ۷ (مهر)،‌ ماه هشتم یا ۸ (آبان)، ماه نهم یا ۹ (آذر)، ماه دهم یا ۱۰ (دی)، ماه یازدهم یا ۱۱ (بهمن)، ماه دوازدهم یا ۱۲ (اسفند).
  • هر ماه، به‌طور تقریبی، ۴ هفته است.
• هفته: هر هفته ۷ روز است.
• روز: هر روز ۲۴ ساعت است.
• ساعت: هر ساعت ۶۰ دقیقه است.
• دقیقه: هر دقیه ۶۰ ثانیه است.
• ثانیه: ثانیه را به‌عنوان کوچک‌ترین واحد در نظر می‌گیریم. البته واحدهای کوچک‌تر از آن وجود دارند که موضوع بحث این آموزش نیستند.

دقت کنید که دانستن این واحدها برای جمع و تفریق ضروری است. برای آشنایی بیشتر با واحدهای زمان، به آموزش «تبدیل واحد زمان — به زبان ساده (+ دانلود فیلم آموزش رایگان)» مراجعه کنید.

جمع و تفریق اعداد مرکب مربوط به زمان

فرض کنید که زمان زیر مدتی است که احمد در یک هفته درس خوانده است:

$$\large 10 \;\;\; 34'\;\;\; 15^{''}$$

که می‌توان آن را این‌گونه نیز نوشت:

$$\large 10 : 34' : 15^{''}$$

چنین نوع نوشتار زمان، این‌گونه خوانده می‌شود: ده و سی‌وچهار دقیقه و پانزده ثانیه.

اکنون، فرض کنید او پنج ساعت و چهل‌وچهار دقیقه و پنجاه ثانیه را در یک هفته به ورزش اختصاص داده است:

$$\large 5 : 44' : 50^{''}$$

می‌خواهیم ببینیم مجموع زمانی را که احمد درس خوانده و ورزش کرده است، محاسبه کنیم.

ابتدا این‌گونه دو زمان را می‌نویسیم:

$$\large \begin {align} 10 : 34' : 15^{''} \\ + \;\;\;\;\;\;\;5 : 44' : 50^{''} \end {align}$$

در ادامه، ثانیه‌ها، دقیقه‌ها و ساعت‌ها را جداگانه با هم جمع می‌کنیم:

$$\large \begin {align} 10 : 34' : 15^{''} \\ + \;\;\;\;\;\;\;5 : 44' : 50^{''} \\ \_ \_\_ \_\_ \_\_ \_\_ \_\_ \_\_ \_\_ \\ 15 : 78' : 65^{''} \end {align}$$

می‌بینیم که برای مجموع ثانیه‌ها عدد $$65$$ و برای مجموع دقیقه‌ها عدد $$78$$ به‌دست آمده است.

چون عدد $$65$$ بزرگ‌تر از $$60$$ است، می‌توانیم آن را به دقیقه تبدیل کنیم.

$$\large \begin {align} 10 : 34' : 15^{''} \\ + \;\;\;\;\;\;\;5 : 44' : 50^{''} \\ \_ \_\_ \_\_ \_\_ \_\_ \_\_ \_\_ \_\_ \\ 15 : 78' : 65^{''} \\ \;\;\;\;\;\;\; - 60 ^{''} \\ \;\;\;\;\;\;\;\_ \_\_\_ \\ 15 : (78+1)' : 5^{''} \\=15 : 79' : 5^{''} \end {align}$$

اکنون به این زمان رسیده‌ایم:

$$\large 15 : 79' : 5^{''}$$

همان‌طور که مشاهده می‌کنید، از ثانیه‌ها $$60$$ تا کم شد و به دقیقه‌های $$1$$ واحد اضافه.

می‌بینیم که دقیقه عدد $$79$$ است و عددی بزرگ‌تر از $$60$$ را نشان می‌دهد. بنابراین، می‌توانیم آن را به ساعت تبدیل کنیم:

$$\large \begin {align} 15 : 79' : 5^{''} \\ \;\;\;-60'\;\;\;\;\;\;\; \\ \_ \_\_ \_\_ \_\_ \_\_ \_\_ \_\_ \_\_ \\ \;\;\;\;\;\;\;(5+1) : 19' : 5^{''} \\ = 16 : 19' : 5^{''} \end {align}$$

مشاهده می‌کنیم که از دقیقه‌ها $$60$$ تا کم شده است و به ساعت‌ها یکی اضافه. بنابراین، جواب جمع دو زمان به‌صورت زیر خواهد بود:

$$\large 16 : 19' : 5^{''}$$

به‌عنوان یک مثال دیگر، فرض کنید ساعت کل زمان تفریح احمد در یک هفته دوازده ساعت و بیست‌وپنج دقیقه و چهل ثانیه بوده است. در این مدت او فیلم دیده و بازی کرده است. می‌خواهیم ببینیم اگر مدت بازی او هشت ساعت و پنجاه دقیقه و چهل‌وپنج ثانیه باشد، او چقدر از زمان تفریحش را به فیلم دیدن اختصاص داده است.

زمان‌ها را این‌گونه می‌نویسیم:

کل زمان تفریح:

$$\large \begin {align} 12 : 25' : 40^{''} \end {align}$$

مدت‌زمان بازی:

$$\large \begin {align} 8 : 45' : 50^{''} \end {align}$$

برای به‌دست آوردن مدت‌زمان فیلم دیدن احمد، باید آن را از کل زمان تفریحش کم کنیم. بدین منظور، تفریق را این‌گونه می‌نویسیم:

$$\large \begin {align} 12 : 25' : 40^{''} \\ - \;\;\;8 : 45' : 50^{''} \end {align}$$

دقت کنید که برای انجام عملیات جمع و تفریق، ثانیه‌ها، دقیقه‌ها و ساعت‌ها را به تفکیک و در یک راستا نوشته‌ایم.

اکنون از تفریق ثانیه‌ها شروع می‌کنیم. می‌بینیم که نمی‌توان $$50$$ ثانیه را از $$40$$ ثانیه کم کرد. برای حل این مشکل، از دقیقه‌ها کمک می‌گیریم. بدین صورت که یکی از دقیقه‌ها کم می‌کنیم، و معادلش، یعنی $$60$$ ثانیه را به ثانیه‌ها اضافه می‌کنیم. بدین ترتیب، تفریق به‌صورت زیر درمی‌آید و می‌توانیم $$50$$ را از $$10$$ کم کنیم که حاصلش را نوشته‌ایم:

$$ \large \begin {align}<br /> 12 : 24' : 100^{''} \\<br /> - \;\;\;8 : 45' : 50^{''} \;\; \\<br /> \_ \_ \_ \_\_ \_ \_\_ \_\_\_\_\_\ \\<br /> : \;\;\;' : 50^{''} \\<br /> \end {align} $$

اما این‌بار که می‌خواهیم دقیقه‌ها را از هم کنیم، می‌بینیم که $$45$$ از $$24$$ بیشتر است. مانند آنچه برای ثانیه‌ها انجام دادیم، $$60$$ واحد به دقیقه‌ها اضافه می‌کنیم و معادلش، یعنی $$1$$ ساعت، را از ساعت‌ها کم می‌کنیم. این یعنی به‌جای $$24$$ دقیقه، $$24+60=84$$ دقیقه ر ا قرار می‌دهیم و به‌جای $$12$$‌ساعت، $$11$$ ساعت را جایگذاری می‌کنیم. بنابراین، می‌توان نوشت:

$$\large \begin {align} 11 : 84' : 100^{''} \\ - \;\;\;8 : 45' : 50^{''} \;\; \\ \_ \_ \_ \_\_ \_ \_\_ \_\_\_\_\_\ \\ 3: 39' : 50^{''}\;\; \\ \end {align}$$

بنابراین، مدت زمانی که احمد به به فیلم دیدن اختصاص داده است، سه ساعت و سی‌ونه دقیقه و پنجاه ثانیه است.

اعداد مرکب مربوط به طول

طول نیز واحدهای زیادی دارد که اعداد مرکب را می‌سازند. از مهم‌ترین و رایج‌ترین واحدهای طول می‌توان به موارد زیر اشاره کرد:

• کیلومتر: هر کیلومتر ۱۰۰۰ متر است.
• متر: هر متر برابر با ۱۰۰ سانتی‌متر است.
• سانتی‌متر: هر سانتی‌متر برابر با ۱۰ میلی‌متی است.
• میلی‌متر: میلی‌متر کوچک‌ترین واحدی است ک هدر زندگی روزمره با آن سر و کار داریم. البته واحدهای کوچک‌تر از میلی‌متر نیز وجود دارند که موضوع این آموزش نیستند.

برای مثال، اگر ۵ کیلومتر پیاده‌روی کنیم، معادل با ۵۰۰۰ متر است. یا اگر قطر یک کتاب ۳ سانتی‌متر باشد، یعنی ۳۰ میلی‌متر است. برای آشنایی بیشتر با واحدهای طول، پیشنهاد می‌کنیم به آموزش «تبدیل واحد طول — به زبان ساده (+ دانلود فیلم آموزش رایگان)» مراجعه کنید.

جمع و تفریق اعداد مرکب مربوط به طول

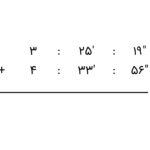
اکنون مثالی را از اعداد مرکب مربوط به طول بررسی می‌کنیم. فرض کنید نسترن و نیکو باید یک نقاشی خیابانی آماده کنند. در طول یک روز، نسترن ۲ متر و ۲۰ سانتی‌متر از آن را آماده کرده است. همچنین، نیکو ۱ متر و ۳۳ سانتی‌متر را رنگ‌آمیزی کرده است. مجموع طولی از دیوار را که نسترین و نیکو با هم رنگ‌ زده‌اند چقدر است؟

برای پاسخ این مثال، باید هر دو مقدار را با هم جمع کنیم. بدین منظور، متر و سانتی‌متر را با کمی فاصله نوشته و جمع را به‌شکل زیر می‌نویسیم:

$$\large \begin {align} 2 \;\;\;\; \; 20 \\ + \;\;\;\;1 \;\;\;\; \; 33 \\ \end {align}$$

برای انجام جمع، ابتدا دو عدد مربوط به سانتی‌متر را با هم جمع می‌کنیم، سپس دو عدد مربوط به متر را. بنابراین، خواهیم داشت:

$$\large \begin {align} 2 \;\;\;\; \; 20 \\ + \;\;\;\;1 \;\;\;\; \; 33 \\ \_\_\_ \_\_\_\_\_\ \\ 3 \;\;\;\; \; 53 \end {align}$$

بنابراین، مجموع طولی که نیکو و نسترن رنگ زده‌اند، ۳ متر و ۵۳ سانتی‌متر است.

اعداد مرکب مربوط به جرم

جرم نیز، مانند کمیت‌های دیگر، واحدهای متنوعی دارد که در ادامه، رایج‌ترین آن‌ها را معرفی می‌کنیم:

• تن: هر تُن برابر با ۱۰۰۰ کیلوگرم است.
• کیلوگرم: هرکیلوگرم برابر با ۱۰۰۰ گرم است.
• گرم: گرم در زندگی روزمره معمولاً کوچک‌ترین واحد جرم است. البته واحدهای دیگری نیز وجود دارند که خارج از موضوع این آموزش هستند.

برای آشنایی بیشتر با واحدهای اندازه‌گیری جرم، به آموزش «تبدیل واحد وزن و جرم — به زبان ساده (+ دانلود فیلم آموزش رایگان)» مراجعه کنید.

جمع و تفریق اعداد مرکب مربوط به جرم

اکنون مثالی را در رابطه با جرم بررسی می‌کنیم.

فرض کنید یک قنادی مقدار ۲۳ کیلوگرم و ۳۵۰ گرم آرد دارد و از آن، مقدار ۷ کیلوگرم و ۵۰۰ گرم را مصرف کرده است. می‌خواهیم محاسبه کنیم که چه مقدار آرد برای قنادی باقی مانده است.

بدین منظور، اعداد مربوط به کیلوگرم و گرم را جدا می‌نویسیم و تفریق زیر را می‌نویسیم:

$$\large \begin {align} 23 \;\;\;\; \; 350 \\ - \;\;\;\; 7 \;\;\;\; \; 500 \end {align}$$

از کوچک‌ترین واحد، یعنی گرم، شروع می‌کنیم. می‌بینیم که $$350$$ از $$500$$ کوچک‌تر است و نمی‌توان تفریق را انجام داد. به همین دلیل، از عدد $$23$$ مربوط به کیلوگرم کمک می‌گیریم. بدین منظور، از $$23$$ کیلوگرم یک کیلوگرم را کم می‌کنیم و معادل آن یک کیلوگرم، یعنی $$1000$$ گرم را به $$350$$ گرم اضافه می‌کنیم. در نتیجه، تفریق به‌صورت زیر درمی‌آید:

$$\large \begin {align} 22 \;\;\;\; \; 1350 \\ - \;\;\; 7 \;\;\;\; \;\;\;\; 500 \end {align}$$

اکنون می‌توانیم گرم‌ها را تفریق کنیم و خواهیم داشت:

$$\large \begin {align} 22 \;\;\;\; \; 1350 \\ - \;\;\; 7 \;\;\;\; \;\;\;\; 500 \\ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ 15 \;\;\;\; \; 850 \;\; \end {align}$$

بنابراین، آنچه از آرد برای قنادی باقی می‌ماند، پانزده کیلوگرم و هشتصد و پنجاه گرم است.

مثال‌های جمع و تفریق اعداد مرکب

در این بخش، چند مثال را از اعداد مرکب حل می‌کنیم.

مثال اول جمع و تفریق اعداد مرکب

احمد ساعت هشت و هفت دقیقه و سی‌وپنج ثانیه وارد کتابخانه شد و ساعت یک و بیست‌وپنج دقیقه و چهل‌وپنج ثانیه از آنجا خارج شد. مدت زمانی را که احمد در کتابخانه بوده است، محاسبه کنید.

حل: برای محاسبه مدت زمان ماندن احمد در کتابخانه، باید زمان ورود او را از زمان خروجش کم کنیم. اول از همه باید دقت کنیم که برای هماهنگ بودن ساختار زمان‌ها، به‌جای ساعت $$1$$ بعدازظهر باید از عدد $$13$$ استفاده کنیم تا در محاسبات به مشکل مواجه نشویم.

نکته مهمی که باید به آن دقت کنید، این است که برای ساعت‌های بعد‌ازظهر که کوچک‌تر از ۱۲ هستند، آن‌ها را با ۱۲ جمع می‌کنیم. برای مثال، ساعت ۳ بعد‌ازظهر معادل $$3 + 12 = 15$$ است.

اکنون به محاسبه تفریق برمی‌گردیم. گفتیم که باید ساعت ورود را از ساعت خروج کم کنیم:

$$\large \begin {align} 13 : 25' : 45^{''} \\ - \;\;\;8 : 7' : 35^{''} \;\; \\ \_ \_ \_ \_\_ \_ \_\_ \_\_\_\_\_\ \\ 5: 18' : 10^{''}\;\; \\ \end {align}$$

می‌بینیم که مدت زمان حضور احمد در کتابخانه ۵ ساعت و ۱۸ دقیقه و ۱۰ ثانیه بوده است.

از این مثال دریافتیم که اگر زمان شروع و پایان چیزی را در اختیار داشته باشیم، می‌توانیم مدت زمان را با استفاده از تفاضل زمان شروع از زمان پایان به‌دست آوریم.

مثال دوم جمع و تفریق اعداد مرکب

نرگس برای درس ریاضی یک ساعت و بیست‌وشش دقیقه و پانزده ثانیه وقت گذاشته است. او همچنین، یک ساعت و سی‌وپنج دقیقه و ده ثانیه را به درس علوم اختصاص داده است. مجموع زمان‌هایی را که نرگس به دو درس اختصاص داده است، محاسبه کنید.

حل: این دو زمان را با هم جمع می‌کنیم و خواهیم داشت:

$$\large \begin {align} 1 : 26' : 15^{''} \\ + \;\;\;\;\;1 : 35' : 10^{''} \\ \_ \_ \_ \_\_ \_ \_\_ \_\_\_\_\_\ \\ \;\;2: 61' : 25^{''} \\ \end {align}$$

می‌بینیم که عدد مربوط به دقیقه از $$61$$ بیشتر شده است. با توجه به اینکه هر $$60$$ دقیقه برابر با $$1$$ ساعت است، $$60$$ دقیقه را از $$61$$ دقیقه کم می‌کنیم و معادل آن، یعنی $$1$$ ساعت را به $$2$$ ساعتی که داریم اضافه می‌کنیم. بنابراین، خواهیم داشت:

$$\large \begin {align} 1 : 26' : 15^{''} \\ + \;\;\;\;\;1 : 35' : 10^{''} \\ \_ \_ \_ \_\_ \_ \_\_ \_\_\_\_\_\ \\ \;\;2: 61' : 25^{''} \\ \;\;=(2+1): (61-60)' : 25^{''} \\ \;\; =3 : 1' : 25^{''} \end {align}$$

در نتیجه، مدت زمانی که نرگس دو درس را مطالعه کرده است، سه ساعت و یک دقیقه و بیست‌وپنج ثانیه بوده.

از این مثال درمی‌یابیم که اگر مدت زمان انجام چند کار داشته باشیم و بخواهیم کل زمانی را که صرف شده محاسبه کنیم، باید مدت‌زمان‌ها را با هم جمع کنیم.

مثال سوم جمع و تفریق اعداد مرکب

فرض کنید می‌خواهیم غذایی برای یک مهمانی بپزیم و به ۱۰ کیلوگرم و ۳۵۹ گرم برنج نیاز داریم. از این مقدار، ۴ کیلوگرم و ۷۴۸ گرم در خانه موجود است. چقدر دیگر باید برنج بخریم تا مقدار مورد نظر را تأمین کنیم؟

حل: برای حل این مثال، باید مقداری که داریم را از مقداری که می‌خواهیم به آن داشته باشیم، کم کنیم. بدین منظور، تفریق زیر را می‌نویسیم:

$$\large \begin {align} 10 \;\;\;\; \; 359 \\ - \;\;\; 4 \;\;\;\; \;\;\;\; 748 \end {align}$$

برای حل این تفریق، باید از واحد کوچک‌تر، یعنی گرم، شروع کنیم و تفریق را انجام دهیم. می‌بینیم که $$359$$ از $$748$$ کوچک‌تر است. بنابراین، باید از کیلوگرم‌ها یک واحد قرض بگیریم. برای این کار، $$1$$ کیلوگرم از $$10$$ کیلوگرم را کم می‌کنیم و معادل آن، یعنی $$1000$$ گرم را به $$359$$ گرم اضافه می‌کنیم. بنابراین، تفریق به‌صورت زیر درمی‌آید:

$$\large \begin {align} 9 \;\;\;\; \; 1359 \\ - \;\;\; 4 \;\;\;\; \;\;\;\; 748 \end {align}$$

اکنون می‌توان تفریق را به‌راحتی انجام داد و نوشت:

$$\large \begin {align} 9 \;\;\;\; \; 1359 \\ - \;\;\; 4 \;\;\;\; \;\;\;\; 748 \\ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ 5 \;\;\;\; \; 611 \;\; \end {align}$$

مثال چهارم جمع و تفریق اعداد مرکب

احمد و حسن زمان مطالعه‌شان در یک هفته را این‌گونه اندازه گرفته‌اند:

• احمد: ۵۰۰ دقیقه
• حسن: ۶ ساعت و نیم

مجموع زمان مطالعه آن‌ها را محاسبه کنید.

حل: همان‌طور که می‌بینیم، زمان مربوط به احمد کاملاً برحسب دقیقه و زمان مربوط به حسن برحسب ساعت است. این دو مدت زمان را به اعداد مرکب تبدیل می‌کنیم، سپس جمع را انجام می‌دهیم.

برای تبدیل $$500$$ دقیقه به عدد مرکب، باید آن را بر $$60$$ دقیقه (معادل یک ساعت) تقسیم کنیم و خارج قسمت را به‌عنوان ساعت و باقیمانده را به‌عنوان دقیقه بنویسیم. اگر این تقسیم را انجام دهیم، می‌بینمیم که به $$8$$ ساعت و $$20$$ دقیقه می‌رسیم.

برای زمان حسن نیز، $$6$$‌ ساعت و نیم را داریم. همان‌طور که می‌دانیم، نیم ساعت برابر با $$30$$ دقیقه است.

بنابراین، جمع و جواب زیر را داریم:

$$\large \begin {align} 8 : 20' \\ + \;\;\;\;\;6 : 30' \\ \_ \_ \_ \_\_ \_ \_\_ \_\_\_\_\_\ \\ \;\;14: 50' \end {align}$$

می‌بینیم که مجموع برابر با $$14$$‌ ساعت و $$50$$‌ دقیقه است.

معرفی فیلم آموزش ریاضی پایه هفتم

یکی از آموزش‌های دوره متوسطه اول فرادرس، آموزش ریاضی پایه هفتم است. این آموزش در ۱۳ ساعت و ۳ دقیقه و در قالب ۹ فصل تهیه و تدوین شده  است. موضوع فصل اول این آموزش راهبردهای حل مساله است. در فصل دوم به عددهای صحیح پرداخته شده است. جبر و معادله موضوع فصل سوم این آموزش ویدیویی است. در فصل چهارم، درباره هندسه و استدلال بحث شده است. شمارنده‌ها و اعداد اول در فصل پنجم معرفی شده‌اند. فصل ششم درباره سطح و حجم است و فصل هفتم به توان و جذر اختصاص یافته است. در فصل هشتم، موضوع بردار و مختصات مورد بررسی قرار گرفته است. در نهایت، در فصل نهم، به مبحث آمار و احتمال پرداخته شده است.

لازم به ذکر است در درس‌های این فیل آموزشی، مثال‌های تکمیلی نیز حل شده است.

• برای مشاهده فیلم آموزش ریاضی پایه هفتم + اینجا کلیک کنید.

جمع‌بندی

در این آموزش، با اعداد مرکب برای زمان، جرم و طول آشنا شدیم. همچنین، با بیان مثال‌های متنوع، نحوه محاسبه جمع و تفریق اعداد مرکب را بیان کردیم.