انتگرال لبگ در ریاضیات | به زبان ساده

در ریاضیات، انتگرال‌گیری (Integration) روی یک تابع با مقادیر نامنفی، در ساده‌ترین حالت، به عنوان سطح زیر منحنی آن تابع (یعنی مساحت بین منحنی و محور مربوط به متغیر) در نظر گرفته می‌شود. «انتگرال لبگ» (Lebesgue Integral) این مفهوم را توسعه داده و انتگرال یک تابع را برحسب یک اندازه (Measure) تعیین می‌کند. از آنجایی که این گونه محاسبه انتگرال در ریاضیات مدرن، «نظریه احتمال» (Probability Theory) و «آنالیز ریاضی» (Mathematical Analysis) اهمیت دارد این نوشتار را به موضوع انتگرال لبگ در ریاضیات اختصاص داده‌ایم.

به منظور آشنایی با نظریه اندازه و اندازه لبگ بهتر است نوشتارهای اندازه لبگ در نظریه اندازه | به زبان ساده و  نظریه اندازه در ریاضیات — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن نوشتارهای فضای متریک و نامساوی مثلثی — به زبان ساده و قضیه تفکیک لبگ در نظریه اندازه — به زبان ساده نیز خالی از لطف نیست.

انتگرال لبگ در ریاضیات

زمانی که انتگرال و مشتق معرفی شدند، برای محاسبه سطح زیر منحنی هموار (مشتق‌پذیر) از انتگرال استفاده کردند، بخصوص زمانی که تابع مربوط به منحنی، یک تابع نامنفی باشد، مساحت بخش پایین منحنی تا محور افقی، همان انتگرال تابع در نظر گرفته می‌شد.

فیلم آموزش مبانی آنالیز حقیقی – جامع و با نکات کاربردی در فرادرس

کلیک کنید

برای توابع شناخته شده، انتگرال براساس قواعد موجود به شکل انتگرال معین معرفی و برای توابع دیگر، نحوه محاسبه انتگرال به صورت عددی و تقریبی ارائه و مورد بهره‌برداری قرار گرفت.

ولی در بعضی از مواقع مانند فرآیندهای حدی در آنالیز ریاضی و تئوری احتمالات، نوع خاصی از انتگرال مورد احتیاج بود که توسط «هنری لبگ» (Henri Lebesgue) ریاضیدان فرانسوی، مبانی آن توسعه یافت، بطوری که حتی در فضاهایی خارج از اعداد حقیقی نیز قابل استفاده است.

به طور کلی، انتگرال لبگ به انتگرال یک تابع نسبت به یک اندازه (Measure) اطلاق می‌شود، بخصوص اگر این اندازه، همان «اندازه لبگ» (Lebesgue Measure) باشد.

مقدمه‌ای بر انتگرال ریمان

همانطور که گفته شد، انتگرال تابع مثبت $$f$$ روی بازه $$(a,b)$$ را می‌توان به صورت سطح زیر منحنی $$f$$‌ تا محور افقی در نظر گرفت. این موضوع بخصوص برای خانواده توابع چند جمله‌ای به خوبی محسوس است.

سطح زیر منحنی برای همه توابع نمی‌تواند موید، انتگرال باشد. روش‌های انتگرال‌گیری پاسخی به این پرسش است که چگونه باید انتگرال را محاسبه کرد. «انتگرال ریمان» (Riemann Integral) یکی از پاسخ‌ها به این مسئله است که توسط «برنارد ریمان» (Bernhard Riemann)، ریاضیدان آلمانی، در قرن ۱۹ ارائه شد. او توسط مجموع دنباله‌ای از مساحت مستطیل‌هایی که بین منحنی تابع و محور افقی تعریف کرد، تقریبی برای انتگرال معرفی نمود. موفقیت تعریفی که او ارائه داد، به علت همخوانی با انتگرال‌های توابع خوش تعریف و همچنین حل انتگرال برای توابع جدید بود. هر چند ریمان به محاسبه حد و همگرایی این دنباله نپرداخت ولی به کمک مطالعات در زمینه «سری‌های فوریه» (Fourier Series) و «تبدیل فوریه» (Fourier Transform) می‌توان همگرایی این دنباله‌ها را مشخص و اثبات کرد.

در مقابل، انتگرال لبگ نشان می‌دهد چه زمانی می‌توانیم حد را به داخل انتگرال برده یا از آن خارج کنیم. این موضوع توسط قضیه‌های موسوم به «همگرایی یکنوا» (Monotone Convergence Theorem) و «همگرایی مغلوب» (Dominated Convergence Theorem) اثبات می‌شود. این قضایا در ادامه متن مورد بررسی قرار خواهند گرفت.

تفسیر شهودی انتگرال از دیدگاه ریمان و لبگ

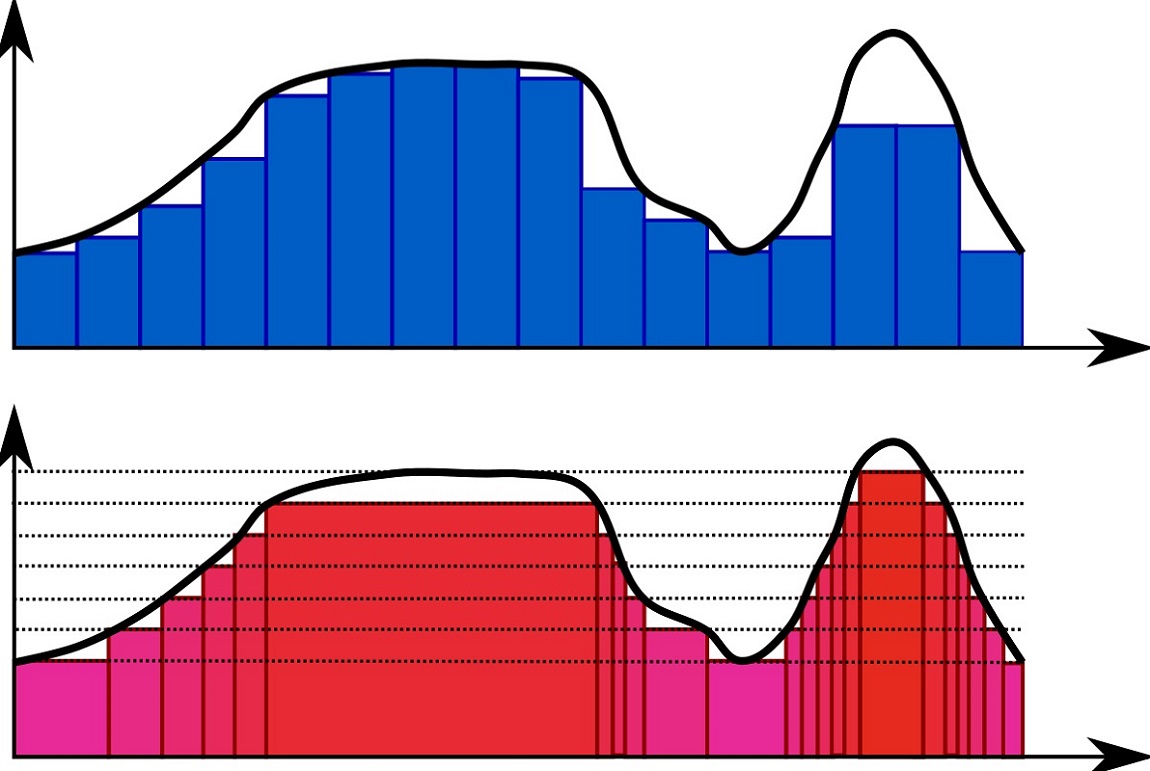
برای درک بهتر روشی که انتگرال ریمان و انتگرال لبگ برای محاسبه انتگرال به کار بردند به سطح زیر منحنی برای یک تابع مثبت با دو رویکرد ریمان و لبگ توجه می‌کنیم. فرض کنید تابعی هموار و دارای پادمشتق (انتگرال‌پذیر) مانند $$f$$ داریم و می‌خواهیم انتگرال آن را روی بازه $$a$$‌ تا $$b$$‌ با شرط $$a$$ بدست آوریم.

در تصویر ۱، نگرش «ریمان-داربکوس» (Reimann-Darbux) برای محاسبه انتگرال چنین تابعی را مشاهده می‌کنید.

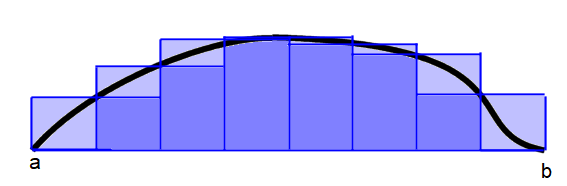
در نظر بگیرید که می‌خواهیم حجم یک کوه را به کمک انتگرال ریمان محاسبه کنیم. سطح دریا را به عنوان مبدا یا همان سطح افق در نظر داشته باشید.

سطح زیرین کوه را به شبکه‌هایی با مساحت ۱ متر مربع تقسیم بندی کنید. ارتفاع کوه در مرکز هر یک از این مربع‌ها در نظر گرفته می‌شود. به این ترتیب حجم یک قطعه از کوه به وسیله ضرب سطح مقطع در ارتفاع، تخمین زده می‌شود. بر همین اساس حجم کوه برابر با مجموع ارتفاع‌ها خواهد بود. پس اگر ارتفاع را با $$f_i$$ در سطح مقطع $$i$$ام در نظر بگیریم، خواهیم داشت:

$$ \large Volume = 1 \text{m^2} \times \sum f_i $$

این بار با رویکرد لبگ به مسئله نگاه می‌کنیم. ابتدا نمودار کانتور (Contour Map) از کوه را ترسیم می‌کنیم. اگر هر یک از این کانتورها با یکدیگر ۱ متر فاصله داشته باشند، سطح هر یک از کانتورها تقریبا برابر با حجم بخشی از کوه خواهد بود. در نتیجه حجم کوه با جمع کردن سطوح کانتور محاسبه می‌شود.

$$\large Volume = \sum \text{Contour's  area } \times 1$$

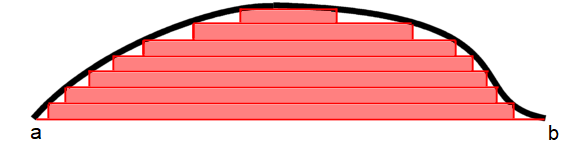
همانطور که دیده می‌شود، در انتگرال ریمان، مقادیر دامنه تابع $$f$$، افراز (Partition) شده در حالیکه در انتگرال لبگ، برد تابع $$f$$‌ افراز خواهد شد.

تعریف رسمی انتگرال لبگ

برای تعریف انتگرال ریمان در اینجا از نماد اندازه $$\mu$$ روی یک مجموعه مثل $$A$$ استفاده می‌کنیم. می‌دانیم که اندازه روی یک مجموعه از اعداد حقیقی، نامنفی است. در نتیجه $$\mu(A)$$ را اندازه $$A$$ می‌نامیم. این اندازه برای مجموعه اعداد حقیقی همان اندازه لبگ (طول فاصله) است.

فیلم آموزش مبانی آنالیز ریاضی – جامع و کاربردی در فرادرس

کلیک کنید

به این ترتیب با افراز برد تابع $$f$$، انتگرال تابع $$f$$ روی بازه یا مجموعه $$A$$ به صورت مجموع سطوح منحنی در هر بازه $$y=t$$ و $$y=t-dt$$ قرار می‌گیرد. به صورت ابتدایی اندازه برای چنین مجموعه‌ای را به صورت زیر نشان می‌دهیم.

$$\large \mu \left(\{ x \mid f(x) > t \}\right)\, d t$$

فرض کنید که

$$\large f^{*}(t) = \mu \left(\{ x \mid f(x) > t \}\right)$$

در این صورت انتگرال لبگ برای تابع $$f$$ به شکل زیر تعریف می‌شود.

$$\large \int f \, d \mu = \int _{0}^{\infty }f^{*}(t) \, d t$$

طرف راست تساوی بالا، انتگرال ریمان و طرف چپ، نشانگر انتگرال لبگ تحت اندازه $$\mu$$ است.

توجه داشته باشید که $$f^*$$ یک تابع نانزولی و نامنفی است. در نتیجه برای انتگرال ریمان یک تابع خوش‌تعریف است که در بازه $$[0,\infty)$$ تغییر می‌کند. برای کلاس توابع خوش‌تعریف (توابع اندازه‌پذیر) تساوی بالا برقرار خواهد بود.

در حالتی که تابع $$f$$ ضرورتا مثبت نباشد، تابع اندازه‌پذیر $$f$$ دارای انتگرال لبگ است اگر سطح بین منحنی $$f$$ و محور افقی، متناهی باشد.  به این ترتیب خواهیم داشت:

$$\large \int |f| \, d \mu < + \infty$$

با وجود این شرط درست به مانند انتگرال ریمان، مقدار انتگرال لبگ روی دو ناحیه محاسبه شده و انتگرال کلی بدست می‌آید.

$$\large \int f \, d \mu = \int f^{+} \, d \mu - \int f^{-} \, d \mu$$

در رابطه بالا، $$f = f^+ - f^-$$ و $$f^-$$ و $$f^+$$ تفکیک تابع $$f$$ به دو تابع نامنفی است که به صورت زیر ساخته می‌شوند.

$$\large {\displaystyle {\begin{alignedat}{3}f^{ + }(x) & = \max\{ f(x), 0 \}&{} = {} & { \begin{cases} f(x),&{\text{if }} f(x) > 0 ,\\ 0 , &{\text{otherwise}} \end{cases}}\\ \\f^{-}(x)& = \max\{-f(x),0\} & {} = {} & {\begin{cases} - f(x),&{\text{if }}f(x) < 0 , \\ 0 , & {\text{otherwise}} \end{cases}} \end{alignedat}}}$$

ساختار انتگرال لبگ

همانطور که گفتیم، در انتگرال لبگ از اندازه لبگ در نظریه اندازه استفاده می‌شود. در نتیجه ابتدا براساس توابع ساده اندازه پذیر لبگ، محاسبه انتگرال آغاز و تعریف شده، سپس مفهوم انتگرال لبگ برای توابع دیگر تعریف و به کار گرفته می‌شود. ساده‌ترین تابع در نظریه اندازه، «تابع نشانگر» (Indicator Function) است که محل آغاز تعریف انتگرال لبگ محسوب می‌شود.

هر تابع ساده (Simple Function) را به کمک ترکیب خطی از تابع نشانگر می‌توان ایجاد کرد. می‌توان نشان داد که تابع نشانگر، لبگ-اندازه‌پذیر است در نتیجه ترکیب خطی از تابع نشانگر که تابع ساده را می‌سازد، نیز اندازه‌پذیر لبگ است.

انتگرال لبگ برای تابع نشانگر

برای تابع مشخصه یا نشانگر $$1_S$$ که در آن $$S$$ یک مجموعه $$\mu$$-اندازه‌پذیر است، مقدار انتگرال لبگ به صورت زیر تعیین می‌شود.

$$\large {\displaystyle \int 1_{S} \, d \mu = \mu (S)}$$

توجه داشته باشید که نتیجه ممکن است شامل $$+\infty$$ نیز باشد مگر آنکه اندازه $$\mu$$‌، متناهی در نظر گرفته شود.

در ادامه به کمک یک مثال، تفاوت انتگرال ریمان و انتگرال لبگ را برای تابع نشانگر روشن‌تر می‌کنیم.

مثال: در این مثال تابع نشانگر اعداد گویا $$1_Q$$ را در نظر می‌گیریم و نشان می‌دهیم که این تابع، انتگرال‌پذیر لبگ بوده ولی انتگرال‌پذیر ریمان نیست.

$$1_Q$$ را تابع نشانگر اعداد گویا در نظر بگیرید. مقدار این تابع برای هر عدد گویا برابر با ۱ و برای اعداد غیرگویا، صفر خواهد بود. چنین تابع را گاهی با نام «تابع دریکله» (Dirichlet Function) نیز می‌شناسند. واضح است که این تابع در هیچ نقطه‌ای پیوسته نیست.

• تابع نشانگر اعداد گویا، انتگرال‌پذیر ریمان روی بازه $$[0,1]$$ نیست. اگر به هر شکل ممکن، بازه $$[0,1]$$ را افراز کنید، به هر حال یک عدد گویا و یک عدد غیرگویا (اصم) در داخل افراز قرار می‌گیرند. زیرا مجموعه اعداد گویا و اصم هر دو فشرده (Dense) در اعداد حقیقی هستند. به این ترتیب «مجموع بالایی داربوکس» (Upper Darboux Sums) همگی برابر با ۱ بوده و مقادیر «جمع پایینی داربوکس» (Lower Darboux Sums) هم صفر هستند. در نتیجه انتگرال ریمان موجود نخواهد بود، زیرا این دو مجموع با یکدیگر برابر نیستند.
• تابع نشانگر اعداد گویا، انتگرا‌ل‌پذیر لبگ روی بازه $$[0,1]$$ است. اندازه لبگ را در نظر بگیرید. در این صورت رابطه زیر برقرار است:

$$\large \int _{[0,1]}1_{\mathbf {Q} } \, d \mu = \mu (\mathbf {Q} \cap [0,1] ) =0$$

رابطه اخیر به این علت برابر با صفر است که مجموعه اعداد گویا، شمارش‌پذیر بوده و می‌دانیم برای چنین مجموعه‌ای، اندازه لبگ صفر است.

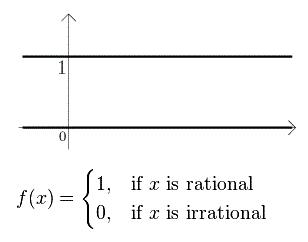
انتگرال لبگ برای تابع ساده

یک تابع ساده به صورت ترکیب خطی از توابع نشانگر ساخته می‌شود. به این ترتیب بین تابع نشانگر یا مشخصه و تابع ساده رابطه زیر برقرار است.

$$\large \sum _{k}a_{k}1_{S_{k}}$$

ضرایب $$a_k$$ مقادیر حقیقی و $$S_k$$ مجموعه‌های $$\mu$$-اندازه‌پذیر و جدا از هم هستند. به این ترتیب با در نظر گرفتن ضرایب مثبت $$a_k$$ می‌توانیم انتگرال توابع ساده را به صورت زیر مشخص کنیم.

$$\large \int \left(\sum _{k}a_{k} 1_{S_{k}} \right) \, d \mu =\sum _{k}a_{k}\int 1_{S_{k}} \, d \mu =\sum _{k}a_{k}\,\mu (S_{k})$$

به این نکته نیز توجه داشته باشید که $$0 \times \infty = 0$$.

نکته: مشخص است که نمایش یک تابع ساده به کمک توابع نشانگر منحصر به فرد نیست ولی خوشبختانه نتیجه انتگرال همیشه یکسان خواهد بود. از طرفی برای آنکه به مشکل $$\infty-\infty$$ دچار نشویم، فرض می‌کنیم که $$\mu(S_k)<\infty$$ و $$a_k \neq 0$$

$$\large f = \sum _{k}a_{k} 1_{S_{k}}$$

اگر $$B$$ یک زیرمجموعه اندازه‌پذیر از مجموعه $$E$$ و $$S$$ نیز یک تابع اندازه‌پذیر ساده باشد، می‌توانیم رابطه زیر را برای محاسبه انتگرال در نظر بگیریم.

$$\large \int _{B} s \, d \mu = \int 1_{B} \, s \, d \mu = \sum _{k} a_{k} \, \mu (S_{k} \cap B)$$

انتگرال لبگ برای توابع نامنفی

فرض کنید که تابع $$f$$، اندازه‌پذیر و نامنفی روی $$E$$ باشد بطوری که مقدار $$+\infty$$ را هم می‌پذیرد. به این ترتیب دامنه تابع نامنفی $$f$$، «مجموعه اعداد حقیقی توسعه یافته» (Extended Real Number Line) است.

انتگرال لبگ تابع $$f$$ را به صورت زیر تعریف می‌کنیم.

$$\large \int _{E}f \, d \mu = \sup \left\{ \, \int _{E} s \, d \mu :0 \leq s \leq f,\ s\ { \text{simple}} \, \right\}$$

حال فرض کنید که $$s_n(x)$$ یک تابع ساده باشد که مقدار آن برابر با $$k/2^n$$‌ است. حال اگر تابع $$f(x)$$ در بازه $$k/2^n$$ و $$(k+1)/2^n$$ قرار داشته باشد، می‌توان نشان داد رابطه انتگرال و حدی زیر برقرار است.

$$\large {\displaystyle \int f\,d\mu = \lim _{n \to \infty } \int s_{n} \, d \mu }$$

رابطه بالا، ارتباط بین انتگرال لبگ و توابع ساده را مشخص می‌کند و انگیزه برای نمایش انتگرال لبگ با استفاده از افراز روی برد تابع را نمایان می‌سازد.

تابع علامت و انتگرال لبگ

برای مشخص کردن انتگرال لبگ توابع علامت، احتیاج به چند تعریف جدید داریم. فرض کنید تابع $$f$$ یک تابع اندازه‌پذیر روی مجموعه اعداد حقیقی توسعه یافته باشد. آنگاه چنین تابعی را به صورت زیر می‌توان نوشت:

$$\large f = f^{+} - f^{-}$$

بطوری که هر یک از این توابع به صورت زیر تعریف می‌شوند. در حقیقت $$f^+$$ و $$f^-$$ تفکیکی از تابع $$f$$ هستند.

$$\large f^{+}( x ) = \begin{cases} f(x) & { \text{if }} f ( x ) > 0 \\ 0 &{ \text{otherwise}} \end{cases}$$

همچنین

$$\large f^{-}(x) = \begin{cases} - f( x ) & { \text{ if }} f( x ) < 0 \\ 0 &{ \text{ otherwise }} \end{cases}$$

توجه داشته باشید که هر دو تابع $$f^-$$ و $$f^+$$، نامنفی بوده و اندازه‌پذیر لبگ هستند. همچنین قدرمطلق تابع $$f$$ نیز به صورت زیر درخواهد آمد.

$$\large | f | = f^{ + } + f^{ - }$$

در این حالت می‌گوییم انتگرال تابع لبگ-اندازه‌پذیر $$f$$ موجود بوده و به صورت مجموعه انتگرال توابع $$f^+$$ و $$f^-$$ محاسبه خواهد شد.

$$\large \min \left( \int f^{ + } \, d \mu , \int f^{ - } \, d \mu \right) < \infty$$

البته موجود بودن انتگرال بالا به شرطی است که یکی از انتگرال‌های زیر، متناهی باشند.

$$\large \int f^{ + } \, d \mu ,\;\;\; \int f^{ - } \, d \mu$$

در این حالت انتگرال $$f$$ را نسبت به اندازه $$\mu$$ به صورت زیر در نظر می‌گیریم.

$$\large { \displaystyle \int f \, d \mu = \int f^{+}\, d \mu - \int f^{ - } \, d \mu }$$

اگر قدرمطلق تابع $$f$$ دارای انتگرال متناهی باشد، آنگاه می‌گوییم تابع $$f$$، انتگرال‌پذیر لبگ است. این موضوع خصوصیات مورد نظر برای انتگرال را درست مانند حالت انتگرال ریمان به ارمغان خواهد آورد.

$$\large \int | f | \, d \mu < \infty$$

انتگرال لبگ برای توابع مختلط

برای توابع مختلط به همین شکل می‌توان انتگرال لبگ را تعریف و مورد استفاده قرار داد. به این ترتیب با تفکیک قسمت حقیقی و موهومی تابع، انتگرال لبگ به صورت زیر تعریف می‌شود.

$$\large \int h \, d \mu = \int f \, d \mu + i \int g \, d \mu$$

که در آن $$h = f+ig$$ بوده و $$f$$ و $$g$$، توابع حقیقی انتگرال‌پذیر هستند.

نکته: یک تابع را انتگرال‌پذیر لبگ گوییم اگر قدرمطلق آن انتگرال‌پذیر لبگ باشد.

خواص اصلی انتگرال لبگ

در ادامه به بعضی از خواص جالب برای انتگرال لبگ خواهیم پرداخت. در اینجا فرض بر این است که توابع $$f$$ و $$g$$، لبگ-اندازه‌پذیر بوده و انتگرال لبگ آن‌ها نیز موجود است.

فیلم آموزش مبانی آنالیز ریاضی – مرور و حل مساله در فرادرس

کلیک کنید

انتگرال توابع یکسان (تقریبا همه جا برابر)

اندازه لبگ و در نتیجه انتگرال لبگ دو تابع را که در مجموعه نقاطی با اندازه لبگ صفر با یکدیگر تفاوت دارند، یکسان در نظر می‌گیرد. به طور دقیق‌تر دو تابع $$f$$ و $$g$$ تقریبا همه جا (Almost Everywhere) یکسان یا برابر هستند اگر رابطه زیر برقرار باشد.

$$\large \mu ( \{ x \in E : f(x) \neq g(x) \} ) = 0$$

رابطه بالا نشان می‌دهد که مجموعه نقاطی که در آن، این دو تابع با یکدیگر تفاوت دارند، دارای اندازه (اندازه لبگ) صفر است.

پس اگر دو تابع لبگ-اندازه‌پذیر نامنفی $$f$$ و $$g$$ (با مقدار $$+\infty$$) تقریبا همه‌جا یکسان باشند ($$f = g , \;a.e$$)، آنگاه:

$$\large \int f \, d \mu = \int g \, d \mu$$

توجه داشته باشید که برابری انتگرال‌ها نیز باید به صورت تقریبا همه‌جا در نظر گرفته شود.

اگر دو تابع $$f$$ و $$g$$ تقریبا همه جا با هم برابر باشند و $$f$$ انتگرال‌پذیر لبگ باشد، آنگاه $$g$$‌ نیز انتگرال‌پذیر لبگ بوده و برعکس. همچنین حاصل انتگرال $$f$$ و $$g$$ نیز با یکدیگر برابر خواهند بود.

ویژگی خطی بودن انتگرال لبگ

دو مقدار حقیقی $$a$$ و $$b$$ را در نظر بگیرید. آنگاه انتگرال رابطه خطی توابع انتگرال‌پذیر $$f$$ و $$g$$ نیز انتگرال‌پذیر بوده و داریم:

$$\large {\displaystyle \int (a f + b g) \, d \mu = a \int f \, d \mu + b \int g \, d \mu }$$

ویژگی یکنوا بودن انتگرال لبگ

فرض کنید که $$f\leq g$$، آنگاه

$$\large \int f \, d \mu \leq \int g \, d \mu$$

خاصیت هم‌گرایی یکنوا در انتگرال لبگ

دنباله $$\{f_k\}_{k \in N}$$ را که از توابع نامنفی اندازه‌پذیر تشکیل شده در نظر بگیرید که به صورت صعودی مرتب شده. به این ترتیب رابطه زیر بین آن‌ها برقرار خواهد بود.

$$\large f_{k}(x) \leq f_{ k + 1 }(x) \quad \forall k \in \mathbb {N} ,\, \forall x \in E$$

آنگاه حد این دنباله در صورت وجود با $$f$$ نشان داده شده و انتگرال‌پذیر لبگ است و همچنین بین انتگرال لبگ آن‌ها نیز می‌توان رابطه زیر را در نظر گرفت.

$$\large {\displaystyle \lim _{k} \int f_{k} \, d \mu = \int \lim_{k} f_k\, d \mu = \int f \, d \mu }$$

البته این موضوع را هم در نظر بگیرید که ممکن است مقدار انتگرال هر کدام از طرفین تساوی، بی‌نهایت باشد. می‌توان به کمک این قضیه نتیجه گرفت که انتگرال حد دنباله‌ای از توابع برابر با حد انتگرال آن دنباله خواهد بود.

لم فاتو برای انتگرال لبگ

باز هم دنباله $$\{f_k\}_{k \in N}$$ را که از توابع نامنفی اندازه‌پذیر تشکیل شده، در نظر بگیرید. آنگاه:

$$\large \int \liminf _{k}f_{k} \, d \mu \leq \liminf_{ k } \int f_{k} \, d \mu$$

باز هم ممکن است هر یک از انتگرال‌های بالا، نامتناهی (بی‌نهایت) باشند.

قضیه همگرایی مغلوب

در قضیه همگرایی مغلوب ابتدا دنباله $$\{f_k\}_{k \in N}$$ که از توابع مختلط اندازه‌پذیر تشکیل شده در نظر گرفته شده و فرض بر این است که این توابع به صورت نقطه‌ای، دارای حد هستند. همچنین تابع انتگرال‌پذیر لبگ $$g$$ نیز با شرط $$|f_k|$$ برای هر $$k$$ را نیز منظور می‌کنند. در نتیجه قدر مطلق توابع این دنباله به $$g$$ کراندار هستند. واضح است که $$g$$ متعلق به فضای $$L^1$$ است.

با شرایط ذکر شده، $$f$$ انتگرال‌پذیر لبگ بوده و داریم:

$$\large \lim _{k}\int f_{k} \, d \mu = \int f\,d \mu$$

تناقض در انتگرال لبگ

از آنجایی که هر تابعی، انتگرال‌پذیر لبگ نیست، گاهی نمی‌توان انتگرال لبگ را محاسبه کرد. ولی البته این موضوع همیشه صحیح نیست. برای مثال تابع $$\frac{\sin x }{x}$$ را روی مجموعه اعداد حقیقی درنظر بگیرید. این تابع انتگرال‌پذیر لبگ نیست، زیرا انتگرال قدرمطلق این تابع متناهی نیست.

$$\large { \displaystyle \int _{- \infty }^{+ \infty } \left| { \frac {\sin(x)}{x}}\right| d x = \infty }$$

فیلم آموزش مبانی آنالیز ریاضی – مرور، حل مثال و تست کنکور ارشد – بخش یکم در فرادرس

کلیک کنید

ولی از طرف دیگر می‌دانیم که انتگرال زیر موجود بوده و به صورت یک انتگرال نامعین قابل محاسبه و متناهی است.

$$\large { \displaystyle \int_{- \infty}^{ + \infty} \dfrac{\sin x}{x} } d x$$

انتگرال بالا برابر با دو برابر «انتگرال دریکله» (Dirichlet Integral) است.

خلاصه و جمع‌بندی

در این نوشتار با انتگرال لبگ در ریاضیات آشنا شدیم. همچنین خصوصیات و اصطلاحاتی که برای مجموعه‌های اندازه‌پذیر لبگ و انتگرال آن وجود دارد، نیز مورد بحث قرار گرفت. با توجه به تعریف انتگرال ریمان و لبگ، مزایا و معایب هر یک از آن‌ها نیز مرور شد. از آنجایی که کاربرد زیادی برای انتگرال لبگ در نظریه احتمال وجود دارد، آگاهی از تعریف اولیه این انتگرال و کاربردهای مربوط به قضیه‌های آن نیز امری مهم برای کسانی است که در آنالیز ریاضی و احتمال دست به قلم هستند. همین موضوع می‌تواند باعث ایجاد انگیزه در نزد کسانی شود که در حوزه احتمال درگیر هستند.