آنالیز واریانس با مقادیر تکراری — از صفر تا صد

تحلیل یا آنالیز واریانس با مقادیر تکراری روشی برای بالا بردن دقت محاسبات و همچنین آزمون فرض روی مقادیر وابسته از چند تیمار است. این تکنیک را می‌توان معادل با «تحلیل واریانس یک طرفه» (One-way ANOVA) در نظر گرفت. ولی با توجه به این نکته که مشاهدات در این حالت، از یکدیگر مستقل نبوده و وابستگی دارند، تفاوت بین آنالیز واریانس یک طرفه با آنالیز واریانس با مقادیر تکراری مشخص می‌شود. در حالتی که از یک عامل یا تیمار در دو سطح استفاده شود، آزمون آنالیز واریانس با مقادیر تکراری را می‌توان همان «آزمون t وابسته زوجی» (Paired sample t -test) محسوب کرد. به دلیل اهمیت بررسی تیمار یا شرایط مختلف روی آزمودنی‌ها، محاسبات و نحوه انجام آزمون در آنالیز واریانس با مقادیر تکراری را موضوع این نوشتار از مجله فرادرس قرار داده‌ایم.

برای آشنایی بیشتر با نحوه تجزیه واریانس و به کارگیری آن برای آزمون فرض بهتر است نوشتارهای دیگر مجله فرادرس مانند تحلیل واریانس (Anova) — مفاهیم و کاربردها و آزمون فرض میانگین جامعه در آمار — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی و متغیر فاکتور (Factor) یا متغیر عامل در R — راهنمای کاربردی نیز خالی از لطف نیست.

آنالیز واریانس با مقادیر تکراری

هر گاه یک «طرح آزمایش» (Experimental Design) را براساس مشاهدات تکراری در سطوح مختلف یک تیمار روی یک آزمودنی انجام دهیم، روش به کار رفته را با «مقادیر تکراری» (Repeated Measure) می‌نامند. از آنجایی که مقدار مشاهده شده برای حالت‌های مختلف تیمار برای هر فرد، وابسته به ویژگی‌های اوست، وابستگی بین مقادیر حاصل بوجود خواهد آمد.

فیلم آموزش آنالیز واریانس با اس پی اس اس SPSS در فرادرس

کلیک کنید

به همین علت تفاوت عمده‌ای که بین تحلیل‌های با مقادیر تکراری نسبت به آزمون‌های بدون تکرار وجود دارد، به کار گرفتن ماتریس همبستگی یا کوواریانس است. به این ترتیب تحلیل واریانس با مقادیر تکراری پیچیده‌تر بوده ولی دقت بیشتری دارد. در این نوشتار به حالت ساده‌ای از آنالیز واریانس خواهیم پرداخت که یک «متغیر وابسته» (Dependent Variable) و یک «متغیر مستقل» (Independent Variable) یا «عامل» (Factor) وجود دارد.

در این آزمون یا روش تحلیلی، متغیر وابسته به صورت «داده‌های کمی» (Quantitative) و متغیر مستقل نیز به شکل «مقادیر کیفی» (Qualitative) از نوع «اسمی» (Nominal) یا «ترتیبی» (Ordinal) در نظر گرفته می‌شوند.

چه وقت از آنالیز واریانس با مقادیر تکراری استفاده کنیم؟

از تحلیل یا آنالیز واریانس با مقادیر تکراری (Repeated Measures ANOVA) برای دو نوع طراحی مطالعه تجزیه و تحلیل استفاده می‌شود. مطالعاتی که یا (1) تغییر در میانگین نمرات بیش از سه یا چند اندازه یا مقدار را در زمان‌های مختلف بررسی می‌کنند، یا (2) اختلاف در میانگین مقادیر یک متغیر کمی، در شرایط مختلف که توسط متغیر عامل تعیین می‌شوند.

به عنوان مثال، برای حالت 1، فرض کنید در مورد تأثیر برنامه تمرین ورزشی 6 ماهه بر فشار خون تحقیق کرده و بخواهید فشار خون را در 3 نقطه زمانی جداگانه (قبل از انجام تمرین، حین و بعد از ورزش) بسنجید. به این ترتیب آنالیز واریانس با مقادیر تکراری به شما امکان می‌دهد یک دوره زمانی را برای هر نوع تمرین ورزشی در نظر گرفته و آزمون یکسان بودن اثر تمرین ورزشی را بر فشار خون، تعیین کنید.

برای حالت 2، ممکن است موضوع در تمایل به خوراک خاصی مورد نظر باشد. فرض کنید افرادی، انواع کیک مختلف (شکلات، کارامل و لیمو) را خورده و به هر کدام براساس طعم و خوشمزگی امتیاز داده‌اند. به یاد داشته باشید که این موضوع متفاوت با دسته‌بندی کردن افراد به سه دسته است که در هر دسته نوع خاصی از کیک مورد آزمون قرار گرفته باشد.

نکته: موضوع مهم مورد این دو طرح تحقیقی، این است که افراد مشابه بیش از یک بار در همان متغیر وابسته اندازه‌گیری می‌شوند. به همین علت این نوع تحلیل را با مقادیر تکراری می‌نامند.

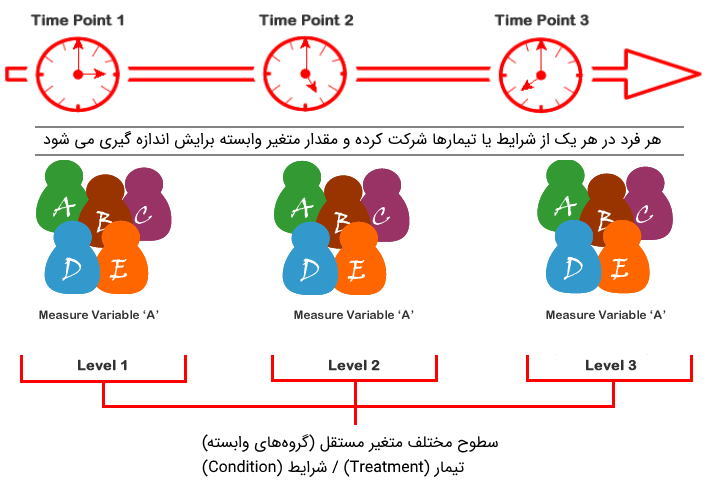
در تجزیه و تحلیل واریانس با مقادیر تکراری، متغیر مستقل دارای مقادیری به نام‌ سطوح (Levels) یا گروه‌های مرتبط (Related Groups) است. در جایی که اندازه‌گیری‌ها با گذشت زمان تکرار شوند، مانند زمان اندازه‌گیری تغییرات فشار خون به دلیل برنامه تمرینی، متغیر مستقل مقاطع زمانی است. هر سطح (یا گروه مرتبط) یک نقطه زمانی خاص را نشان می‌دهد. از این رو، برای مطالعه اثر تمرین ورزشی، سه نقطه زمان وجود خواهد داشت و هر نقطه زمانی یک سطح از متغیر مستقل است. تصویر ۱، چنین طرحی را با مقادیر تکراری با سه دوره زمانی نشان داده است.

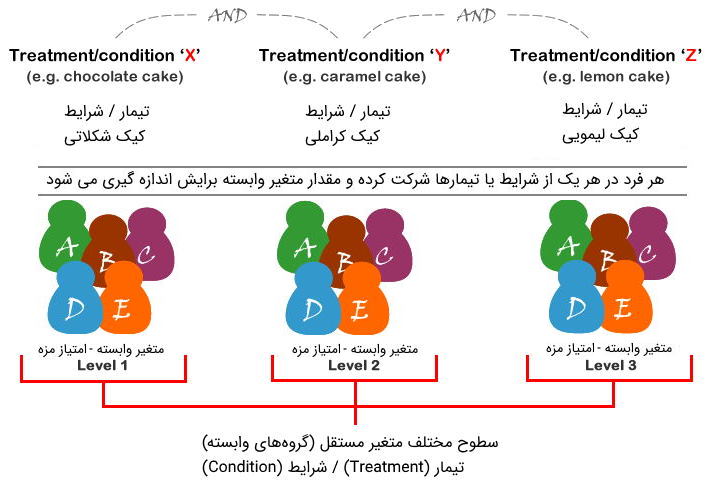
در جایی که اندازه‌گیری‌ها در شرایط مختلف انجام می‌شود، شرایط یا گروه‌های مرتبط، توسط سطوح مختلف متغیر مستقل تعیین می‌شوند. به عنوان مثال، نوع کیک، متغیر مستقل با مقادیر یا سطوح «شکلاتی»، «کاراملی »و «کیک لیمو» محسوب شده و در طرح آنالیز واریانس با مقادیر تکراری به کار گرفته می‌شوند. در تصویر ۲، ارتباط سطوح متغیر عامل (متغیر مستقل) و متغیر وابسته (کمی) دیده می‌شود.

نکته: لازم به ذکر است که اغلب به سطوح متغیر مستقل شرایط (Conditions) یا تیمار (Treatment) گفته می‌شود. همچنین چنین تحلیل اغلب به عنوان «تحلیل درون آزمودنی» (Within Subject Analysis) مورد بحث قرار می‌گیرد.

در تصویر ۲، مثالی از یک طرح آنالیز واریانس با مقادیر تکراری خاص را دیدیم و ارتباط بین متغیر عامل و وابسته را درک کردیم. نحوه در نظر گرفتن مقادیر در یک جدول اطلاعاتی نیز در جدول ۱ نمایش داده شده است. معمولا چنین ساختاری را برای به کارگیری نرم‌افزارهای محاسبات آماری برای حل مسئله آنالیز واریانس با مقادیر تکراری به کار می‌برند.

جدول ۱، اطلاعاتی برای آنالیز واریانس با مقادیر تکراری

جدول 1، مطالعه‌ای را با شش آزمودنی (Experiments) یا Case با نشانگرهایی S1 تا S6  انجام می‌دهد که تحت سه نوع شرط یا در سه نقطه زمانی (T1 تا T3) به عنوان سطوح مختلف متغیر عامل اجرا می‌شود. همانطور که قبلاً اشاره شد، عامل نیز می توانست به جای «زمان یا شرایط»، دارای برچسب «تیمار» باشد. واضح است که همه آنها به یک چیز مربوط می‌شوند: «افراد تحت اندازه‌گیری‌های مکرر در هر سه زمان مختلف و یا تحت شرایط/ تیمارهای مختلف قرار گرفته‌اند.»

فرض‌های آماری در آنالیز واریانس با مقادیر تکراری

همانطور که در قبل نیز اشاره شد، آنالیز واریانس، تکنیکی برای درک تفاوت گروه‌ها است. در نتیجه اگر $$k$$ گروه (تیمار یا جامعه) را در نظر گرفته باشیم، آزمون فرض (Null Hypothesis) در این حالت به شکل زیر نوشته می‌شود. واضح است که $$k$$ تعداد جامعه‌ها یا تعداد سطوح تیمار (متغیر عامل) بوده و $$\mu_i$$ نیز میانگین گروه یا سطح تیمار $$i$$ام است.

$$\large H_0: \mu_1 = \mu_2 = \mu_3 = \ldots = \mu_k$$

فیلم آموزش آمار ریاضی 2 – آزمون فرض در فرادرس

کلیک کنید

فرض صفر در اینجا نشانگر یکسان بوده میانگین گروه‌ها یا بی‌تاثیری عامل (تیمار) در تغییر میانگین $$\mu$$ جامعه‌ها، برای هر سطح از تیمار است. از طرفی فرض مقابل (Alternative Hypothesis) به شکل زیر نوشته می‌شود.

$$\large H_1: \mu_i \neq \mu_j, \;\;\text{ for some i , j }$$

برای مثال برای تمرینی ورزشی، فرضیه صفر ($$H_0$$) این است که فشار خون در تمام نقاط زمان (قبل، 3 ماه و 6 ماه بعد از تمرین) یکسان است. فرضیه مقابل ($$H_a$$ یا $$H_1$$) در این صورت می‌تواند تفاوت در میانگین فشار خون در یک یا چند نقطه زمانی باشد.

متاسفانه، آنالیز واریانس با مقادیر تکراری در صورت رد فرض صفر، توضیحی در مورد گروه‌های دارای اختلافات در اختیارمان قرار نمی‌دهد. زیرا این تحلیل، یک آزمون در مورد وجود یا عدم تساوی میانگین‌ها است. پس از آنکه فرض صفر توسط آنالیز واریانس رد شد، می‌توانیم آزمون‌های دنباله‌ای یا تعقیبی را که به مقایسه‌های دوتایی می‌پردازد، اجرا کنیم. همانطور که در مثال مربوط به تمرین ورزشی گفته شد، شرایط یا روش‌های مختلف تمرینی و نه نقاط زمانی تحقیق صورت می‌گیرد. اگر آنالیز واریانس با مقادیر تکراری اختلاف بین گروه‌ها را از نظر آماری معنادار تشخیص دهد، می‌توان آزمون‌های تعقیبی (Pos-Hoc) را اجرا کرده تا دقیقاً مشخص می‌شود که اختلافات معنی‌دار، بین چه گروه یا تیمارها رخ داده است.

پشت پرده و منطق به کارگیری آنالیز واریانس با مقادیر تکراری

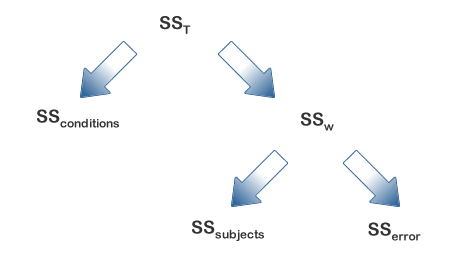
همانطور که می‌دانید تحلیل واریانس یا ANOVA بر تجزیه پراکندگی کل (تغییر پذیری) استوار است. از این رو آنالیز واریانس با مقادیر تکراری نیز به همین شکل عمل خواهد کرد. به یاد بیاورید که ANOVA پراکندگی کل را به دو بخش «تغییرپذیری بین گروه‌ها» ($$SS_b$$) و «تغییرپذیری درون گروه‌ها» ($$SS_w$$)، افراز می‌کند. در تصویر ۳، شیوه اجرای این افراز را به خوبی نمایش داده شده است.

در این طرح، «پراکندگی درون گروهی» ($$SS_w$$) به عنوان مولفه خطا ($$SS_{error}$$) تعریف شده است. پس از تقسیم کردن هر یک از مقادیر مربوط به «مجموع مربعات» (Sum of Squares)، بر درجه‌های آزادی (Degree of Freedom) مناسب هر یک از افرازها، «میانگین مربعات بین گروه‌ها» ($$MS_b$$) و «درون گروه‌ها» ($$MS_w$$) تعیین می‌شوند و آماره $$F$$ به عنوان نسبت $$MS_b$$ به $$MS_w$$ (یا $$MS_{error}$$) محاسبه شده و به عنوان آماره آزمون مورد استفاده قرار می‌گیرد.

$$\large \text{Independent ANOVA}: \;\;F = \dfrac{MS_b}{MS_w} = \dfrac{MS_b}{MS_{error}}$$

آماره $$F$$ برای حالتی که از تحلیل واریانس با مقادیر تکراری استفاده می‌کنیم به صورت زیر محاسبه خواهد شد.

$$\large \text{Repeated Measures ANOVA}: \;\; F = \dfrac{MS_{conditions}}{MS_{error}}$$

مزیت استفاده از ANOVA با اندازه‌های مکرر (تکراری) این است که «پراکندگی درون گروهی» ($$SS_w$$)، یا همان «پراکندگی خطاها» ($$SS_{error}$$) را در یک طرح آنالیز واریانس مستقل (بین آزمودنی‌ها) بیان را به دو بخش تفکیک می‌کند. به این ترتیب عبارت خطا در ANOVA با اندازه‌های تکراری باعث کاهش خطا شده و بخشی از آن توسط «پراکندگی درون آزمودنی‌ها» ($$SS_{subjects}$$)، افراز می‌شود.

این موضوع را در تصویر 4 به خوبی مشاهده خواهید کرد. این امر به معنای افزایش مقدار آماره $$F$$ است زیرا مخرج کسر مربوط به این آماره کاهش یافته و منجر به افزایش قدرت آزمایش برای تشخیص تفاوت‌های مهم بین آزمودنی‌ها است. در ادامه این متن به کمک یک مثال، جزئیات بیشتری مورد بحث قرار خواهد گرفت.

از جنبه محاسباتی باید توجه داشت که پارامترهای تغییرپذیری یا پراکندگی ناشی از تفاوت بین گروه‌ها ($$SS_{conditions}$$) و تغییرپذیری یا پراکندگی در گروه‌ها ($$SS_W$$) را دقیقاً به مانند ANOVA بین آزمودنی‌ها (مستقل) انجام می‌دهیم.

با این وجود، با تحلیل واریانس با مقادیر تکراری (تحلیل واریانس با اندازه مکرر)، از آنجا که در هر گروه یا سطح از متغیر مستقل، اندازه‌گیری متغیر وابسته برای همه آزمودنی‌ها صورت می‌گیرد، می‌توانیم به دلیل تفاوت‌های فردی یا بین آزمودنی‌ها، مقدار «پراکندگی بین آزمودنی‌ها» که در $$SS_{subjects}$$ باز تاب می‌یابد را از پراکندگی «درون گروهی» ($$SS_w$$) حذف کنیم.

هر سطح از متغیر عامل یا مستقل را یک بلوک در نظر بگیرید. یعنی هر آزمودنی به سطحی از عامل تبدیل می‌شود. سپس پراکندگی خطا را برحسب پراکندگی درون گروهی و پراکندگی آزمودنی‌ها بدست می‌آوریم. این کار باعث کاهش پراکندگی درون گروهی (یا عبارت خطا) شده و در نتیجه مدل حاصل، خطای کمتری خواهد داشت.

آنالیز واریانس با مقادیر مستقل: $$SS_{error} = SS_W$$

آنالیز واریانس با مقادیر تکراری: $$SS_{error} = SS_W - SS_{subjects}$$

حال اگر «پراکندگی بین آزمودنی‌ها» (Between-Subjects) را حذف کنیم، جمله مربعات خطا ($$SS_{error}$$، بازتاب تغییرات هر مشاهده را در هر سطح از متغیر عامل، خواهد بود. به این ترتیب این میزان تغییرپذیری را می‌توان تقابل اثر عامل روی آزمودنی‌ها به شکل شرطی در نظر گرفت. به بیان دیگر $$SS_{error}$$ میزان تاثیرپذیری آزمودنی‌ها را نسبت به شرایط یا متغیر عامل نشان می‌دهد.

با توجه به اینکه ما پراکندگی بین آزمودنی‌ها را حذف کرده‌ایم، $$SS_{error}$$ جدید، فقط نشانگر تنوع یا پراکندگی آزمودنی‌ها در هر یک از شرایط است. ممکن است این موضوع را به عنوان اثر متقابل آزمودنی تحت شرایط تشخیص داد. یعنی برای مثال این مقدار مشخص می‌کند که چگونه افراد نسبت به شرایط مختلف واکنش نشان می‌دهند.

به یاد داشته باشید که آزمودنی (مشاهدات) بیشتری در طرح ANOVA مستقل وجود دارد در حالیکه با همین تعداد مشاهدات درجه آزادی در تحلیل واریانس با مقادیر تکراری متفاوت است.

توجه داشته باشید که در طرح ANOVA مستقل، درجه آزادی جمله خطا برابر با ($$n-k$$) است در حالیکه برای طرح ANOVA با مقادیر تکراری به شکل $$(n-1)(k-1)$$ خواهد بود.

در تصویر 4، نمودار تفکیک پراکندگی کل را برای آنالیز واریانس با اندازه‌های تکراری مشاهده می‌کنید.

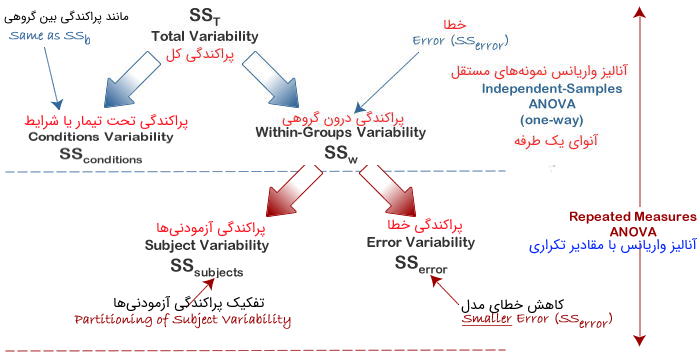
محاسبات مربوط به آنالیز واریانس با مقادیر تکراری

برای آنکه نمایشی از نحوه محاسبات در تحلیل یا آنالیز واریانس با مقادیری تکراری را نمایش دهیم، از یک مثال کمک خواهیم گرفت. این مثال به بررسی با ۶ آزمودنی و سه سطح از متغیر مستقل می‌پردازد.

جدول اطلاعاتی را به صورت جدول ۲، در نظر بگیرد. میزان تناسب اندام برحسب دو نوبت یا دوره ورزشی برای شش نفر اندازه‌گیری شده است. قبل از انجام تمرینات ورزشی امتیاز تناسب اندام این آزمودنی‌ها، اندازه‌گیری شده و در ستون «قبل از تیمار» ثبت شده، بعد از گذشت سه ماه از تمرین ورزشی نیز میزان امتیاز تناسب اندام آن‌ها در ستون‌های سه ماهه و شش ماهه قرار گرفته است.

جدول ۲: محاسبات مربوط به آزمودنی‌ها در آنالیز واریانس با مقادیر تکراری

در ادامه، بسیاری از محاسبات را بر طبق جدول ۲ انجام داده و به همین جهت به آن زیاد مراجعه خواهیم کرد.

در قسمت قبلی با مفهوم $$SS_{conditions}$$ آشنا شده‌اید. از آنجایی که در این مثال زمان یا دوره‌های زمانی فعالیت ورزشی به عنوان متغیر مستقل در نظر گرفته شده، آن را به صورت $$SS_{time}$$‌ می‌نامیم.

برای محاسبه آماره F، باید $$SS_{conditions}$$ و $$SS_{error}$$ را محاسبه کنیم. بخش اول یعنی $$SS_{conditions}$$ یا همان $$SS_{time}$$ را می‌توان مستقیماً و به راحتی محاسبه کرد (همانطور که در ANOVA مستقل با عنوان $$SS_b$$ این کار صورت می‌پذیرد).

اگرچه $$SS_{error}$$ را نیز می توان مستقیماً محاسبه کرد، ولی در مقایسه با بدست آوردن آن از طریق اطلاعات مربوط به سایر مجموع مربع‌ها روش مستقیم سخت‌تر است. $$SS{error}$$ را می‌توان به هر دو روش زیر محاسبه کرد:

$$\large SS_{error} = SS_w - SS_{subjects}$$

یا

$$\large SS_{error} = SS_T - SS_{conditions} - SS_{subjects}$$

هر دو روش برای محاسبه آماری F مستلزم محاسبه $$SS_{conditions}$$ و $$SS_{subjects}$$ است، اما در این صورت می‌توان $$SS_{error}$$ را با محاسبه اولیه $$SS_T$$ یا $$SS_w$$ تعیین کرد.

محاسبه $$SS_{time}$$

همانطور که قبلاً ذکر شد، محاسبه $$SS_{time}$$ همانند $$SS_b$$ در ANOVA مستقل است و می‌تواند به صورت زیر بیان شود:

$$\large SS_{time} = SS_b = \sum_{i = 1}^k n_i (\overline{x}_i \ - \overline{x})^2$$

مشخص است که در رابطه بالا، $$\overline{x_i}$$‌، میانگین تیمار $$i$$ام و $$\overline{x}$$ هم میانگین کل است. $$k$$ نیز تعداد تیمارها را نشان می‌دهد. همچنین $$n_i$$ هم، تعداد آزمودنی‌ها در سطح $$i$$ام تیمار یا شرایط $$i$$ام است.

با توجه به مقادیر مربوط به مثال گفته شده، نتیجه محاسبه $$SS_{time}$$ به شکل زیر خواهد بود.

$$SS_{time} = SS_b = 6 [ (42.8-45.9)^2 + (45.3-45.9)^2 + (49.7-45.9)^2 ] \\ = 6[9.61 + 0.36 + 14.44 ] = 143.44$$

توجه کنید در مثال ما، با یک «طرح اندازه‌گیری مکرر» (Repeated Measures) مواجه هستیم، که به شکل متوازن اجرا شده، به این معنی که $$n_i$$ در هر سطح از متغیر عامل یکسان فرض شده. به بیان دیگر، تعداد آزمودنی‌ها در سطوح مختلف، یکسان در نظر گرفته شده است.

از این رو، ما به راحتی می‌توانیم نتیجه مربع تفاضل‌ها هر گروه را در این تعداد ضرب کنیم. برای تجسم بهتر محاسبات فوق، ارقام جدول زیر به کار می‌آید.

محاسبه $$SS_w$$

پراکندگی درون گروهی (Within Group) نیز طبق جدول ۲ و محاسبات مشابه در ANOVA‌ به صورت زیر خواهد بود.

$$\large SS_w = \sum_1 (x_{i1}-\overline{x}_1)^2 + \sum_2 (x_{i2} - \overline{x}_2)^2 + \cdots + \sum_k (x_{ik} - \overline{x}_k)^2$$

به یاد داشته باشید که $$x_{i1}$$ مشاهده $$i$$ام از سطح تیمار اول است. به این ترتیب $$xـ{ij}$$‌، مشاهده $$i$$ام از تیمار $$j$$ام خواهد بود. واضح است که $$i$$ از یک تا $$n_i$$ تغییر کرده و $$j$$ نیز از ۱ تا $$k$$ مقدار دهی می‌شود. طبق جدول ۲، نتیجه محاسبات برای $$SS_w$$ به صورت زیر خواهد بود،

$$\large SS_w = \sum_1 (x_{i1} - \overline{x}_1)^2 + \sum_2 (x_{i2} - \overline{x}_2)^2 + \sum_3 (x_{i3}-\overline{x}_3)^2$$

که مقدار آن به شکل زیر محاسبه می‌شود.

$$SS_w = [(45 - 42.8)^2 +(42 42.8)^2 +( 36 - 42.8)^2 + (39 - 42.8)^2 + (51 - 42.8)^2 + (44 - 42.8)^2 ] + \\ [(50 - 45.3)^2 + (42-45.3)^2 + (41 - 45.3)^2 + (35 - 45.3)^2 + (55 - 45.3)^2 + (49 - 45.3)^2 + \\ [ (55 - 49.7)^2 + (45- 49.7)^2 + (43 - 49.7)^2 + (40 - 49.7)^2 + (59 - 49.7)^2 + (56 - 49.7)^2 = 715.5$$

جدول زیر، مولفه‌های مهم در این محاسبه را مطابق با جدول ۲، نشان می‌دهد.

محاسبه $$SS_{subjects}$$

همانطور که در قبل نیز توضیح داده شد، هر آزمودنی را به صورت یک بلوک در نظر می‌گیریم. به بیان دیگر هر تیمار را به عنوان سطوح مختلف یک متغیر مستقل یا فاکتور فرض کرده که در اینجا به آن «آزمودنی‌ها» (Subjects) می‌گوییم. به این ترتیب مجموع مربعات آزمودنی‌ها به صورت زیر حاصل می‌شود.

$$\large SS_{subjects} = k \cdot \sum(\overline{x_i} - \overline{x}) ^2$$

با توجه به مثال گفته شده، مقدار $$SS_{subjects}$$ به صورت زیر محاسبه خواهد شد.

$$SS_{subjects} = 3 [(50 - 45.9)^2 + (43 - 45.9)^2 + (40 - 45.9)^2 + (38 - 45.9)^2 + (55 - 45.9)^2 + (49.7 - 45.9)^2 ] = 658.3$$

جدول زیر، مولفه‌های مهم در این محاسبه را مطابق با جدول ۲، نشان می‌دهد.

محاسبه $$SS_{error}$$

با توجه به محاسبات قبلی و ارتباطی که بین «مجموع مربعات خطا» ($$SS_{error}$$) و «مجموع مربعات آزمودنی‌ها» ($$SS_{subjects}$$) و «مجموع مربعات درون آزمودنی» ($$SS_w$$) برقرار است، خواهیم داشت:

$$\large SS_w = SS_{subjects} + SS_{error}$$

به این ترتیب مجموع مربعات خطا برابر است با:

$$\large SS_{error} = SS_w - SS_{subjects}$$

پس برای مثال ذکر شده نتیجه به صورت زیر خواهد بود.

$$\large SS_{error} = 715.5 - 658.3 = 57.2$$

محاسبه میانگین مربعات پراکندگی و آماره $$F$$

برای تعیین میانگین مربعات برای زمان ($$MS_{time}$$) کافی است مجموع پراکندگی برحسب این عامل را بر درجه آزادی مرتبط با آن، یعنی $$(k - 1)$$ تقسیم کنیم. البته توجه دارید که $$k$$ در اینجا نشانگر مقاطع زمانی مختلف است.

فیلم آموزش درس رگرسیون 1 – رگرسیون خطی در فرادرس

کلیک کنید

در این حالت با توجه به مثال گفته شده، خواهیم داشت:

$$\large MS_{times} = \dfrac{SS_{times}}{(k-1)}$$

که به توجه به مقادیر بدست آمده در جدول۲، به نتیجه زیر خواهیم رسید.

$$\large MS_{times} = \dfrac{143.44}{(2)} = 71.72$$

به همین ترتیب نیز میانگین پراکندگی خطا ($$MS_{error}$$) را بدست خواهیم آورد. فقط توجه داشته باشید که درجه آزادی در این بخش برابر با $$(k-1)(n-1)$$ است. واضح است که $$n$$ تعداد آزمودنی‌ها و $$k$$ نیز تعداد سطوح متغیر عامل (زمان) است.

$$\large MS_{error} = \dfrac{SS_{error}}{(n-1)(k-1)}$$

اگر مقادیر محاسبه برای پراکندگی آزمودنی‌ها را طبق محاسبه قبلی در رابطه بالا به کار ببریم، نتیجه به شکل زیر در خواهد آمد.

$$\large MS_{error} = \dfrac{71.72}{(5 \times 2)} = 5.72$$

در انتها نیز محاسبه آماره $$F$$ به شکل زیر خواهد بود.

$$\large F = \dfrac{MS_{time}}{MS_{error}}$$

به در نظر گرفتن نتایج حاصل در صورت و مخرج این کسر، آماره $$F$$ برای مثال به شکل زیر حاصل می‌شود.

$$\large F = \dfrac{71.72}{5.72} = 12.53$$

حال زمان آن فرا رسیده است که مقدار آماره حاصل از مثال را با توزیع $$F$$ با درجه آزادی‌ها محاسبه شده، مقایسه کنیم. چنانچه مقدار آماره $$F$$ حاصل از نمونه تصادفی، بزرگتر از صدک ($$1-\alpha/2$$)ام توزیع $$F$$ باشد، نتیجه آماره در ناحیه بحرانی قرار گرفته و فرض صفر را رد می‌کنیم. در غیر اینصورت دلیلی بر رد فرض صفر نخواهیم داشت.

پیدا کردن صدک توزیع $$F$$ را از طریق نرم‌افزارهای محاسبات آماری یا جدول‌های این توزیع می‌توان صورت داد. ولی اغلب به کمک مقدار احتمال (p-Value) نسبت به فرض صفر تصمیم‌گیری می‌کنیم.

گزارش نتایج حاصل از ANOVA با مقادیر تکراری

در بیشتر مواقع، خروجی محاسباتی در ANOVA، مقدار آماره $$F$$ و درجه‌های آزادی آن است. البته بهتر است «مقدار احتمال» (p-Value) نیز در کنار آن گزارش شود. در این صورت معمولا مقادیر زیر را در گزارش تحقیق آماری، ذکر می‌کنیم.

$$\large F(df_{time}, df_{error}) = F - value, \;\;\; p = p-value$$

به این ترتیب با توجه به مثال گفته شده نتایج را به صورت زیر بیان خواهیم کرد.

$$\large F(2,10) = 12.53 , \;\;\; p = 0.002$$

این مقادیر نشان دهنده رد فرض صفر در سطح آزمون ۵٪ هستند. در نتیجه فرض مقابل یعنی نابرابری حداقل یکی از میانگین‌ها مورد پذیرش قرار می‌گیرد. در گزارش آماری می‌توان این موضوع را به دو شکل گزارش کرد.

• از لحاظ آماری، اثر طول زمان ورزش بر کاهش وزن معنی‌دار است، $$F(2,10) = 12.53, \;\; p = 0.002$$.

یا

• برنامه ورزش ۶ ماهه در میزان کاهش وزن معنی‌دار است زیرا، $$F(2,10) = 12.53, \;\; p = 0.002$$.

نمایش جدولی نتایج آنالیز واریانس با مقادیر تکراری

به طور معمول، نتیجه ANOVA با مقادیر تکراری به جای یک گزاره نوشتاری یا متنی، به صورت یک جدول ارائه می‌شود که براساس آن به راحتی می‌توان نسبت به تایید یا رد فرض صفر، اقدام کرد. البته در گزارشات علمی نتیجه را به صورت متنی نیز ذکر می‌کنند ولی در آن به جدول ANOVA استناد می‌شود.

بیشتر نرم‌افزارهای آماری مانند SPSS، نتیجه ANOVA را به صورت جداول گزارش می‌دهند که تقریبا مشابه با جدول ۳ است. انجام این عمل به کاربر امکان می‌دهد درک کاملی از تمام محاسباتی که توسط این نرم افزارها انجام شده است، بدست آورد. جدول ۳، جدول آنالیز واریانس را برای مقادیر تکراری نشان می‌دهد.

جدول ۳: آنالیز واریانس با مقادیر تکراری و جدول ANOVA

گاهی سطر مربوط به آزمودنی‌ها (Subjects) و تغییرات کل از جدول تحلیل واریانس حذف می‌شوند. به این ترتیب فقط عناصر اصلی در محاسبات ظاهر شده و کاربر خود باید بقیه شاخص‌ها را به کمکم مقادیر ظاهر شده، محاسبه کند. جدول ۴ نظیر چنین جدولی را نمایش داده است.

جدول ۴: جدول آنالیز واریانس برای مثال

بیشتر نرم‌افزارهای محاسبات آماری نیز خروجی مشابه جدول ۴، برای آنالیز واریانس تولید می‌کنند.

افزایش توان در آنالیز واریانس با مقادیر تکراری

همانطور که در قبل نیز بیان شد، یکی از مزایایی استفاده از ANOVA با مقادیر تکراری افزایش دقت و توان آزمون در مقایسه‌های چندتایی به شکل ANOVA با مشاهدات مستقل است. این امر با کاهش میانگین مربعات خطا ($$MS_{error}$$) صورت می‌گیرد که در مخرج کسر آماره $$F$$ قرار دارد. به یاد دارید که در تحلیل واریانس با مقادیر تکراری، «اختلاف بین گروهی» ($$SS_{subject}$$) بوسیله رابطه‌ای که با «اختلاف درون گروهی» ($$SS_{within}$$) دارد، مجموع مربعات خطا ($$SS_{error}$$) را به صورت زیر مشخص می‌کنند.

$$\large SS_{error} = SS_{within} - SS_{subject}$$

بر طبق مثالی که ارائه کردیم، $$F(2,10) = 12.53 , \;\; p = 0.02$$ بدست آمد. در نتیجه فرض صفر، یعنی برابری میانگین‌ها، رد می‌شود.

فیلم آموزش آزمون های فرض میانگین جامعه در اس پی اس اس SPSS در فرادرس

کلیک کنید

حال تصور کنید که به جای استفاده از آزمون ANOVA با مقادیر تکراری، از طرح ANOVA یک طرفه استفاده می‌کردیم. آنگاه درجه‌های آزادی آماره $$F$$ و مقدار احتمال به صورت $$F(2,15) = 1.504 , \;\; p= 0.254$$ حاصل می‌شدند. واضح است که در این حالت برابری میانگین‌ها که فرض صفر را تشکیل می‌دهد، رد نخواهد شد. به تصویر ۶ توجه کنید. این تصویر به خوبی برتری آزمون ANOVA با مقادیر تکراری را نسبت به ANOVA یک طرفه (One-way ANOVA) نشان می‌دهد. حتی دیده می‌شود که نتایج این دو روش آزمون، ممکن است کاملا با یکدیگر تناقض داشته باشند.

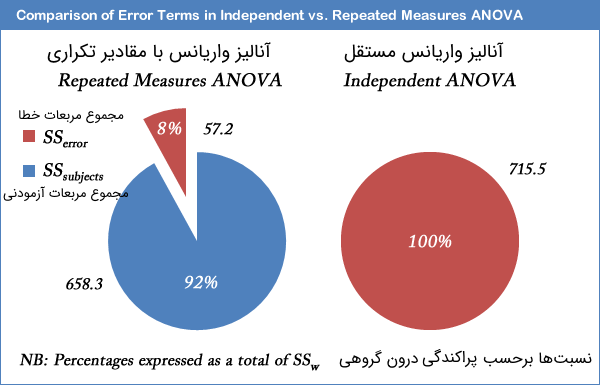
به این موضوع توجه داشته باشید که افزایش درجه آزادی $$SS_W$$‌ نسبت به $$SS_{error}$$، لزوما باعث افزایش مقدار آماره $$F$$ نخواهد شد. به هر حال افزایش مقدار $$SS_{subject}$$ باعث کاهش سهم تغییرات توسط $$SS_{error}$$ خواهد شد که این خود بیانگر مناسب بودن مدل انتخابی (نسبت به مدل تحت فرض صفر) است.

اندازه اثر در ANOVA با مقادیر تکراری

یکی از شاخص‌هایی که در صورت رد فرض صفر، یعنی رد برابری میانگین در سطوح مختلف متغیر تیمار، مورد استفاده قرار می‌گیرد، «اندازه اثر» (Effect Size) است. به این ترتیب مشخص می‌شود که میزان مطابقت با فرض صفر چقدر است. هر چه اندازه اثر زیادتر باشد، نشانه دهنده دوری از فرض صفر است.

فیلم آموزش متاآنالیز یا فراتحلیل Meta-Analysis با SPSS در فرادرس

کلیک کنید

معمولا برای نمایش اثر بخشی تیمارها، از اندازه اثر در گزارشات علمی استفاده می‌شود. برای مثال «مربع اتا جزئی» (Partial Eta-Squared) یکی از شاخص‌های سنجش اندازه اثر است. نحوه محاسبه آن به صورت زیر است.

$$\large {\displaystyle \eta^2_p = \dfrac{SS_{effect} }{SS_{effect} + SS_{error} } }$$

البته اگر گروه‌ها یا سطوح متغیر عامل را به صورت شرایط (Conditions) در نظر بگیریم، شیوه محاسبه به صورت زیر نمایش داده می‌شود.

$$\large {\displaystyle \eta^2_p = \dfrac{SS_{conditions} }{SS_{conditions} + SS_{error} } }$$

همچنین اگر متغیر مستقل، مقاطعی از زمان را مشخص کرده باشد که در آن اندازه‌گیری متغیر وابسته رخ داده، شیوه محاسبه اندازه اثر به شکل زیر خواهد بود.

$$\large {\displaystyle \eta^2_p = \dfrac{SS_{time} }{SS_{time} + SS_{error} } }$$

پیش‌فرض‌های آنالیز واریانس با مقادیر تکراری

به مانند دیگر آزمون‌های آماری، پیش‌فرض‌هایی نیز برای ANOVA با مقادیر تکراری وجود دارد. وجود چنین شرایطی به نتایج حاصل از این آزمون قوت بیشتری می‌دهد. هر چند در بیشتر نرم‌افزارهای محاسبات آماری، ممکن است آزمون بدون توجه به این گونه پیش‌فرض‌ها صورت می‌گیرد، ولی کاربر باید خود پس از اجرای آزمون، از صحت این ویژگی‌ها در داده‌ها اطمینان حاصل کند. در صورتی که این شرایط برای داد‌ه‌ها وجود نداشته باشد، نمی‌توان فرضیه‌های حاصل از آزمون فرض را به جامعه آماری نسبت داد. در ادامه به دو پیش‌فرض مهم در این رابطه پرداخته‌ایم.

پیش‌فرض نرمال بودن در آنالیز واریانس با مقادیر تکراری

یکی از پیش‌فرض‌های مهم در اجرای ANOVA و بخصوص ANOVA با مقادیر تکراری، وجود «توزیع نرمال» (Normal Distribution) برای متغیر وابسته در هر سطح از متغیر مستقل است. روش‌های مختلفی برای مشخص کردن یا مطابقت توزیع جامعه آماری به کمک نمونه‌گیری وجود دارد. اغلب چنین آزمون‌هایی را به «آزمون نرمالیتی» (Normality Test) می‌شناسیم.

به کمک این آزمون‌ها، مشخص می‌شود که آیا متغیر وابسته در هر یک از تیمارها، توزیع نرمال داشته یا خیر. البته شاید کمی انحراف از توزیع نرمال را بتوان برای انجام آزمون تحلیل واریانس نادیده گرفت، ولی باید «چولگی» (Skewness) و «کشیدگی» (Kurtosis) در نمودار فراوانی متغیر وابسته مورد بررسی قرار گیرد تا مطمئن شد که این انحراف شدید نیست.

برای بررسی توزیع متغیر وابسته (یا باقی‌مانده‌های مدل) بهتر است نوشتارهای آزمون نرمال بودن داده (Normality Test) — پیاده سازی در پایتون یا آزمون شاپیرو ویلک (Shapiro-Wilk Test) — به زبان ساده را مطالعه کنید.

پیش‌فرض کروی بودن در آنالیز واریانس با مقادیر تکراری

مفهوم «کروی بودن» (Sphercity)، برای ANOVA با مقادیر تکراری به همان معنی «همگنی» (Homogenity) در آنالیز واریانس است. به این ترتیب مشخص می‌شود که آیا واریانس بین گروه‌ها یکسان است یا خیر. در حقیقت ماتریس کوواریانس تفکیک شده باید دارای مقادیر یکسانی روی قطر اصلی باشد.

در نرم‌افزار محاسبات آماری علوم اجتماعی SPSS، هنگام استفاده از ANOVA با مقادیر تکراری امکان به کارگیری «آزمون کرویت موچلی» (Mauchly's Test of Sphercity)، به عنوان یک روش برای اندازه‌گیری کروی بودن متغیر وابسته (یا باقی‌مانده‌ها) وجود دارد. «آزمون کرویت موچلی» با مقادیر بزرگ برای آماره، فرض یکسان بودن واریانس (یا ماتریس کوواریانس) را در بین گروه‌ها رد می‌کند. در صورتی که فرض کرویت رد شود، برای اجرای آنالیز واریانس با مقادیر تکراری، به آماره «گرینهاوس-گیسر» (Greenhouse-Geisser) توجه کرده و طبق آن آزمون تساوی بین گروه‌های تیمار را انجام می‌دهیم.

برای مثالی که در بالا به آن پرداختیم، همین وضعیت رخ داده است. از آنجا که فرض کرویت نقض شده است، $$\chi^2 (2) = 22.115 ، p <.0005$$، بنابراین، از آماره تصحیح شده «گرینهاوس-گیسر» استفاده شده است. اثر معنی‌داری از زمان بر غلظت کلسترول وجود داشت. واضح است که مقدار آماره $$F$$ برابر با، $$F (171.1,38) = 21.032, \;\; p < 0.0005$$ است.

خلاصه و جمع‌بندی

در این نوشتار با اصول اولیه و نحوه به کارگیری و محاسبات مربوط به آنالیز واریانس با مقادیر تکراری آشنا شدیم. همانطور که دیدید، طرحی که برمبنای اندازه‌های تکراری اجرا شود، از دقت بیشتری نسبت به طرح‌های ساده برخوردار است ولی پیچیدگی طرح و محاسبات آن، ممکن است باعث شود که کمتر محققان از این گونه طرح‌ها استفاده کنند.

پیش فرض‌های اولیه برای اجرای چنین آزمونی نیز تقریبا با آزمون ANOVA یکسان است. ولی به یاد داشته باشید که در اینجا مشاهدات ممکن است به یکدیگر وابسته بوده و در نتیجه به جای ماتریس واریانس به ماتریس کوواریانس بین متغیرهای عامل، مواجه هستیم. از طرفی تجزیه ماتریس کوواریانس به جای ماتریس واریانس صورت گرفته و در صورت استقلال مشاهدات، نتیجه‌ای مشابه با آزمون ANOVA پدید خواهد آمد. در نوشتار دیگری از مجله فرادرس به انجام آزمون آنالیز واریانس با مقادیر تکراری در SPSS خواهیم پرداخت.