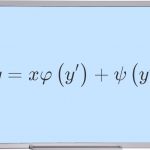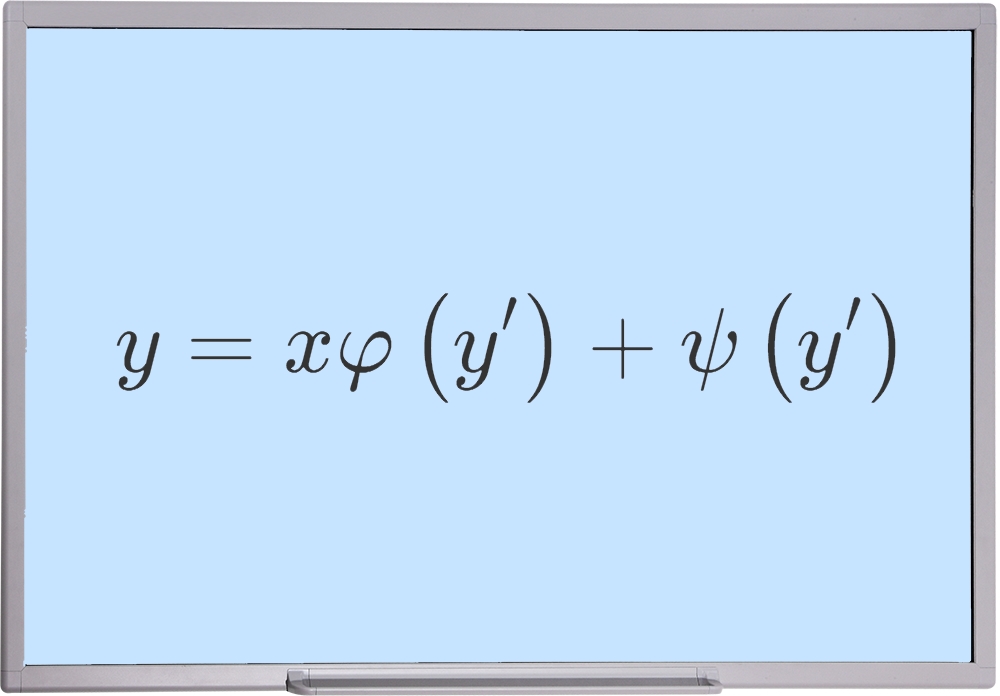معادله لاگرانژ — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های پیشین مجله فرادرس، درباره معادلات دیفرانسیل بحث و روش‌های حل معادلات دیفرانسیل مرتبه اول را بررسی کردیم. معادله لاگرانژ نوع خاصی از معادلات دیفرانسیل مرتبه اول است که در این آموزش به معرفی آن می‌پردازیم.

معادله لاگرانژ

معادله‌ای به فرمِ زیر را در نظر بگیرید:

$$\large y = x \varphi \left ( { y ’ } \right ) + \psi \left ( { y ’ } \right )$$

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

که در آن، $$\varphi \left( {y’} \right)$$ و $$\psi \left( {y’} \right)$$ توابعی معلوم و در بازه‌ای مشخص مشتق‌پذیرند. این معادله، «معادله لاگرانژ» (Lagrange Equation) نامیده می‌شود.

با قرار دادن $$y’ = p$$ و مشتق‌گیری نسبت به $$x$$، جواب عمومی معادله به فرم پارامتری زیر است:‌

$$\large \left\{ \begin {array} {l} x = f \left ( { p , C } \right) \\ y = f \left ( { p , C } \right ) \varphi \left ( p \right ) + \psi \left ( p \right ) \end{array} \right .$$

به شرط اینکه:

$$\large \varphi \left ( p \right ) – p \ne 0$$

که در آن، $$p$$ یک پارامتر است.

اگر شرط $$\varphi \left ( p \right ) – p \ne 0$$ نقض شود، ممکن است معادله لاگرانژ‌ یک جواب تکین داشته باشد. جواب تکین به صورت زیر بیان می‌شود:

$$\large y = \varphi \left ( c \right ) x + \psi \left ( c \right )$$

که در آن، $$c$$ ریشه معادله $$\varphi \left ( p \right ) – p=0$$ است.

مثال‌ها

در این بخش، دو مثال مربوط به معادله دیفرانسیل لاگرانژ بیان می‌کنیم.

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

مثال ۱

جواب‌های عمومی و تکین معادله دیفرانسیل $$y = 2 x y ’ – 3 { \left ( { y ’ } \right ) ^ 2 }$$ را بیابید.

حل: این معادله، یک معادله لاگرانژ است و آن را با استفاده از دیفرانسیل‌گیری حل می‌کنیم.

تساوی $$y’ = p$$ را در نظر می‌گیریم. بنابراین، معادله را می‌توان به صورت زیر نوشت:

$$\large y = 2 x p – 3 { p ^ 2 } .$$

با دیفرانسیل‌گیری از دو سمت معادله بالا، داریم:

$$\large { d y = 2 x d p + 2 p d x } - { 6 p d p . }$$

می‌توانیم $$dy$$ را با $$pdx$$ جایگزین کنیم:

$$\large { { p d x = 2 x d p } + { 2 p d x – 6 p d p , \; \; } } \Rightarrow { – p d x = 2 x d p – 6 p d p . }$$

با تقسیم تساوی بالا بر $$p$$، می‌توان معادله زیر را نوشت (بعد از آن باید جواب بودن $$p=0$$ را برای معادله اصلی بررسی کنیم):

$$\large { - d x = \frac { { 2 x } } { p } d p – 6 d p , \; \; } \Rightarrow { \frac { { d x } } { { d p } } + \frac { 2 } { p } x – 6 = 0 . }$$

همان‌طور که می‌بینیم، یک معادله خطی برای $$x(p)$$ به دست می‌آید. عامل انتگرال‌ساز به صورت زیر است:

$$\large { u \left ( p \right ) = \exp \left ( { \int { \frac { 2 }{ p } d p } } \right ) } = { \exp \left ( { 2 \ln \left | p \right | } \right ) } = { \exp \left ( { \ln { { \left | p \right | } ^ 2 } } \right ) } = { { \left | p \right | ^ 2 } } = { { p ^ 2 } . }$$

جواب عمومی معادله خطی برابر است با:

$$\large { x \left ( p \right ) } = { \frac { { \int { { p ^ 2 } \cdot 6 d p } + C } } { { { p ^ 2 } } } } = { \frac { { \frac { { 6 { p ^ 3 } } } { 3 } + C } } { { { p ^ 2 } } } } = { 2 p + \frac { C } { { { p ^ 2 } } } . }$$

با قرار دادن عبارت بالا به جای $$x$$ در معادله لاگرانژ، داریم:

$$\large { y } = { 2 \left ( { 2 p + \frac { C } { { { p ^ 2 } } } } \right ) p – 3 { p ^ 2 } } \\ \large = { 4 { p ^ 2 } + \frac { { 2 C } } { p } – 3 { p ^ 2 } } = { { p ^ 2 } + \frac { { 2 C } } { p } . }$$

بنابراین، جواب عمومی پارامتری، با دستگاه معادلات زیر تعریف می‌شود:

$$\large \left \{ \begin {array} {l} x \left ( p \right ) = 2 p + \frac { C } { { { p ^ 2 } } } \\ y \left ( p \right ) = { p ^ 2 } + \frac { { 2 C } } { p } \end {array} \right . .$$

علاوه بر این، ممکن است معادله لاگرانژ یک جواب تکین داشته باشد. با حل معادله $$\varphi \left ( p \right ) – p = 0$$، ریشه زیر به دست می‌آید:

$$\large { 2 p – p = 0 , \; \; } \Rightarrow { p = 0 . }$$

در نتیجه، جواب تکین با تابع خطی زیر بیان می‌شود:

$$\large { y = \varphi \left ( 0 \right ) x + \psi \left ( 0 \right ) } = { 0 \cdot x + 0 } = { 0 . }$$

مثال ۲

جواب‌های عمومی و تکین معادله دیفرانسیل $$2 y – 4 x y ’ - \ln y ’ = 0$$ را بیابید.

فیلم آموزش ریاضیات مهندسی پیشرفته – جامع و با نکات مهم در فرادرس

کلیک کنید

حل: با در نظر گرفتن $$y’ = p$$، می‌توان نوشت:

$$\large 2 y = 4 x p + \ln p .$$

با دیفرانسیل گرفتن از دو طرف معادله بالا داریم:

$$\large { 2 d y = 4 x d p + 4 p d x } + { \frac { { d p } } { p } . }$$