معادلات دیفرانسیل حاکم بر پدیده های فیزیکی — به زبان ساده

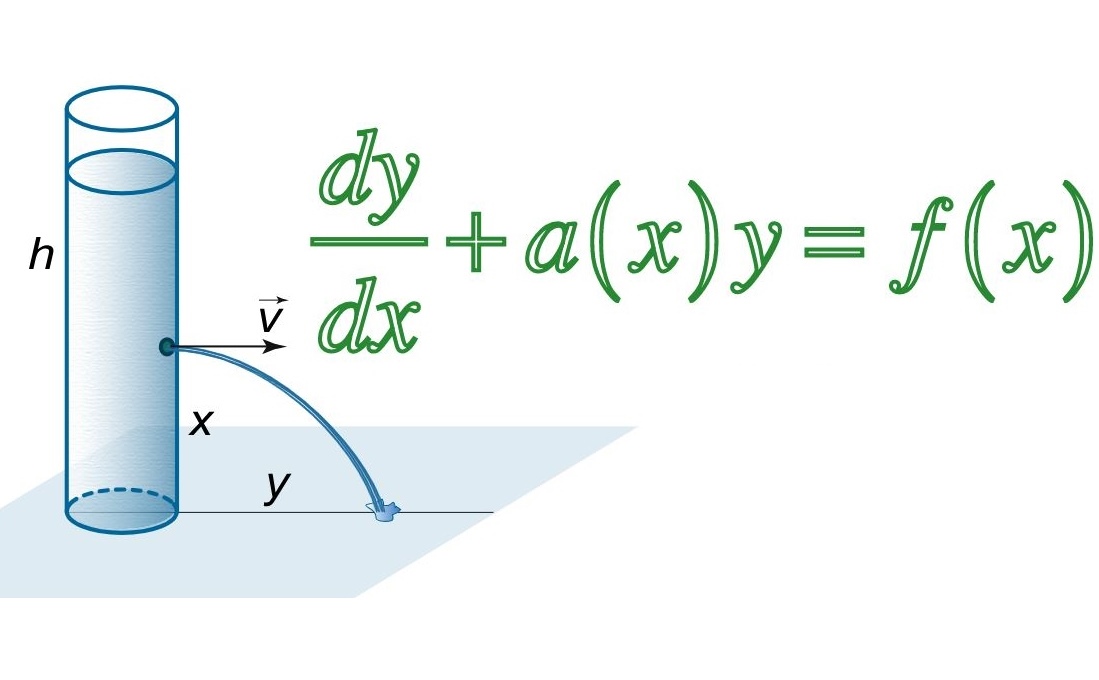
پیش‌تر در وبلاگ فرادرس مفاهیم مربوط به معادلات دیفرانسیل توضیح داده شدند. اما همان‌طور که از فیزیک دبیرستان نیز می‌دانیم برای برخی از پدیده‌های طبیعی می‌توان یک رابطه بیان کرد. واقعیت آن است که این روابط، پاسخ‌های معادله دیفرانسیلی هستند که بر پدیده حاکم است. اما اکثر پدیده‌های فیزیکی غیرخطی هستند. از این رو بدست آوردن پاسخ آن‌ها مشکل بوده و معمولا به صورت عددی این معادلات حل شده و پاسخ آن‌ها بدست می‌آید. در این مطلب قصد داریم تا در مورد معادلات دیفرانسیل حاکم در مدل‌سازی پدیده‌های فیزیکی صحبت کنیم.

پدیده‌های فیزیکی و معادلات دیفرانسیل

پیش‌تر در وبلاگ فرادرس در مورد روابط حاکم به حرکت پرتابی صحبت کردیم. این روابط در ادامه بیان شده‌اند:

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

$$ \begin {gather*} \large x = x _ 0 + \bar {v} t \\~\\ \large \bar {v} = \frac { v _ 0 + v } { 2 }
& \\~\\ \large v = v _ 0 + a t & \\~\\ \large x = x _ 0 v _ 0 + v _ 0 t + \frac { 1 } { 2 } a t ^ 2 & \\~\\ \large v ^ 2=v _ 0 ^ 2 + 2 a ( x - x _ 0 ) \end {gather*} $$

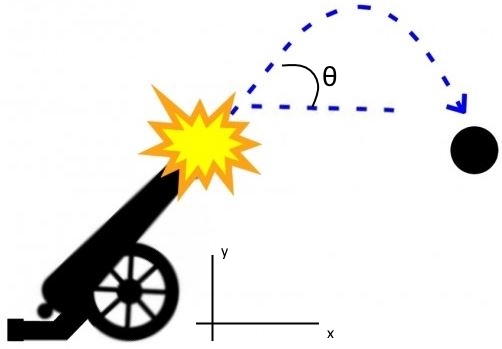
اما این سوال مطرح می‌شود که آیا همواره می‌توان یک پدیده فیزیکی را به صورت تابعی مشخص نوشت؟ اگر پاسخ این سوال مثبت بود تنها با استفاده از توابع ریاضی می‌شد یک هواپیما، خودرو و یا هر وسیله دیگری را طراحی کرد. باید بدانید که برای هر پدیده فیزیکی می‌توان یک معادله دیفرانسیل نوشت؛ اما برای هر پدیده فیزیکی الزاما نمی‌توان یک تابع واضح بیان کرد؛ در حقیقت روابط مربوط به حرکت پرتابی نیز پاسخ‌های معادله دیفرانسیل حرکت هستند.

تعیین میزان نمک حل شده

در این مسئله مقدار ماده‌ای معین -و احتمالا جامد- را بررسی خواهیم کرد که در مایعی (معمولا آب) حل شده باشد. خودِ مایع می‌تواند از یک محفظه خارج شده یا به محفظه وارد شود. فرض کنید $$Q(t)$$ نشان دهنده میزان ماده حل شده در مایع باشد. بدیهی است $$Q$$ وابسته به زمان است. بنابراین هدف بدست آوردن تابع $$ Q ( t ) $$ است.

فیلم آموزش ریاضی فیزیک ۱ در فرادرس

کلیک کنید

مهم‌ترین فرضی که در این‌جا صورت گرفته، یکنواخت بودن توزیع ماده در سیال است. البته در صورت غیریکنواخت بودن توزیع ماده در سیال نیز می‌توان مسئله را بررسی کرد، اما بدست آوردن معادله و پاسخ آن دشوارتر خواهد شد.

در ابتدا فرض کنید آبی که ماده‌ای نیز در آن حل شده با نرخ مشخصی به یک مخزن وارد شده و با نرخی دیگر از آن خارج می‌شود. در این صورت قانون پایستگی جرم را می‌توان به صورت زیر بیان کرد:

 نرخ مایع خارج شده از مخزن - نرخ مایع وارد شده به مخزن = نرخ تغییرات

تنها با استفاده از مفهوم بیان شده در بالا می‌توان معادله دیفرانسیل حاکم بر این پدیده را بدست آورد. البته در ادامه نحوه بدست آوردن معادلات دیفرانسیل حاکم بر پر و خالی شدن مخزن را بررسی خواهیم کرد.

مثال ۱

سوال: مخزنی به ظرفیت $$1500$$ لیتر را در نظر بگیرید که حجم اولیه آب موجود در آن برابر با $$600$$ لیتر است. هم‌چنین فرض کنید مقدار نمک حل شده در آن برابر با $$ 5 $$ کیلوگرم باشد.

فیلم آموزش ریاضی فیزیک ۲ در فرادرس

کلیک کنید

با فرض این‌که آب با نرخ $$ \begin {gather*} 9 \ kg/h \end {gather*} $$ به مخزن وارد شده و با نرخ $$ \begin {gather*} 6 \ kg/h \end {gather*} $$ از آن خارج شود،  هنگامی که مخزن از آب پر شود، میزان نمک موجود در مخزن چقدر خواهد بود؟ هم‌چنین فرض کنید میزان چگالی نمک موجود در آبِ ورودی مطابق با رابطه $$ \begin {gather*} \frac { 1 } { 5 } \left ( { 1 + \cos \left ( t \right ) } \right ) \end {gather*} $$ تغییر می‌کند.

پاسخ: در اولین قدم باید بگوییم که چگالی نمک به صورت نسبت جرم نمک به حجم آب در نظر گرفته می‌شود. بنابراین جرم نمک وارد شده به مخزن برابر است با:

$$ \begin {gather*} \left( 9 \right)\left( {\frac{1}{5}\left( {1 + \cos \left( t \right)} \right)} \right) \end {gather*} $$=نرخ نمک ورودی به مخزن

بدیهی است که عدد $$9$$ در رابطه فوق نشان دهنده نرخِ جرم آبِ ورودی به مخزن است. هم‌چنین می‌توان گفت چگالی جرمی نمک در مخزن، در لحظه $$t$$ برابر است با:

$$ \begin {gather*} \large \frac {Q ( t ) } { 600 + 3 t } \end {gather*} $$

بنابراین نرخ نمک خارج شده از مخزن برابر است با:

$$ \begin {gather*} \large ( 6 ) * \frac {Q ( t ) } { 600 + 3 t } \end {gather*} $$= نرخ نمک خارج شده

لذا معادله دیفرانسیل توصیف کننده نرخ تغییرات خالص جرم نمک در مخزن را می‌توان به صورت زیر بیان کرد:

$$ \begin {align*} \large Q ^ { \prime } \left( t \right) & \large = \left( 9 \right)\left( {\frac{1}{5}\left( {1 + \cos \left( t \right)} \right)} \right) - \left( 6 \right)\left( {\frac{{Q\left( t \right)}}{{600 + 3t}}} \right)\hspace{0.25in} , \ \ Q \left ( 0 \right ) = 5 \\ \large Q ^ {\prime} \left ( t \right) & \large = \frac{9}{5}\left( {1 + \cos \left( t \right ) } \right ) - \frac{{2Q\left( t \right)}}{{200 + t}}\hspace{0.25in} , \ \ Q\left( 0 \right) = 5 \end {align*}$$

عبارت فوق، معادله‌ دیفرانسیلی خطی از مرتبه اول محسوب شده و حل آن مشکل نخواهد بود. در مطلب معادله دیفرانسیل خطی نحوه بدست آوردن پاسخ این گونه از معادلات توضیح داده شده است. در ادامه پاسخ معادله فوق بدست آمده است.

$$ \large Q ^ { \prime } \left ( t \right ) + \frac { { 2 Q \left ( t \right ) } } { { 200 + t } } = \frac {9} {5} \left ( { 1 + \cos \left ( t \right ) } \right ) $$

$$ \large \mu \left( t \right) = {{e}^ {\LARGE {\int{{\frac{2} { { 200 + t } } d t } } } }} = { { \Large { { e } } ^ { 2 \ln \left( { 200 + t} \right) } } } = { \left ( { 200 + t } \right ) ^ 2 } $$

$$ \large \int { { { { \left ( { { { \left ( { 200 + t } \right ) } ^ 2 } Q \left ( t \right ) } \right ) } ^ \prime } \, d t } } \, = \int{{\frac {9} {5} { { \left ( { 200 + t } \right ) } ^ 2 } \left ( { 1 + \cos \left ( t \right ) } \right ) d t } } $$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

$$\begin {align*} \large { \left ( { 200 + t } \right)^2}Q\left( t \right) & = \large \frac{9}{5}\left( {\frac{1}{3}{{\left( {200 + t} \right ) } ^ 3 } + {{\left( {200 + t} \right)}^2}\sin \left( t \right ) + 2 \left ( { 200 + t } \right ) \cos \left ( t \right ) - 2\sin \left( t \right)} \right) + c \\ Q \left ( t \right) & = \large \frac { 9 } { 5 } \left( {\frac { 1 } { 3 }\left( {200 + t } \right ) + \sin \left( t \right) + \frac { { 2 \cos \left( t \right ) } }{ { 200 + t}} - \frac { { 2 \sin \left( t \right ) } } { { { { \left( {200 + t} \right)} ^ 2 } } } } \right) + \frac { c } { { { { \left( {200 + t} \right)}^ 2 } } }\end{align*} $$

به منظور بدست آوردن ثابت $$c$$، می‌توان زمان $$t=0$$ را در رابطه فوق قرار داده و ثابت را بدست آورد. با انجام این کار ثابت $$c$$ برابر می‌شود با:

$$\begin {align*} \large 5 = Q\left( 0 \right) = \frac {9} {5} \left ( { \frac {1} {3}\left ( {200} \right) + \frac { 2 } { { 200}}} \right) + \frac{c}{{{{\left( {200} \right)}^2 } } }\hspace {0.25in}c = - 4600720 \end{align*} $$

نهایتا مقدار نمک موجود در آب، در لحظه $$t$$ برابر است با:

$$\begin {align*} \large Q\left( t \right) = \frac{9}{5}\left( {\frac{1}{3}\left( {200 + t} \right) + \sin \left( t \right) + \frac { { 2 \cos \left( t \right ) } } { { 200 + t}} - \frac { {2\sin \left( t \right)}} { { {{\left( {200 + t} \right)}^2 } } } } \right) - \frac{{4600720}} { { {{\left( {200 + t} \right)}^2}}} \end{align*} $$

از طرفی واضح است که میزان آب موجود در مخزن در لحظه $$t$$ برابر با $$\begin {align*} 600+3t \end{align*} $$ است. با برابر قرار دادن این رابطه با $$1500$$ مشخص می‌شود که پس از $$300$$ ساعت مخزن پر می‌شود. با قرار دادن این عدد در رابطه فوق، مقدار نمک در این لحظه برابر می‌شود با:

$$\begin {align*} \large Q \left( { 300 } \right ) = 279.797{\mbox{ kg}} \end{align*} $$

نمودار زیر مقدار نمک موجود در مخزن را با گذشت زمان نشان می‌دهد.

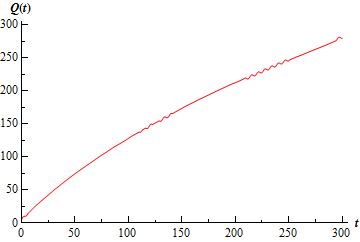
مثال ۲

سوال: جسمی به جرم $$50 \ kg$$ با سرعت اولیه‌ $$10 \ m/s$$ از سطحی که در ارتفاع $$100 \ m$$ قرار گرفته، به سمت بالا پرتاب می‌شود. اگر نیروی وارد به جسم طبق رابطه $$5 v^2$$ بدست آید، در این صورت سرعت جسم را نسبت به زمان $$t$$ بدست آورید.

فیلم آموزش ریاضی فیزیک ۳ در فرادرس

کلیک کنید

پاسخ: این مسئله از دو بخش تشکیل شده است. بخش اول زمانی است که جسم به سمت بالا حرکت می‌کند. در این مرحله نیروی آیرودینامیکی به سمت پایین خواهد بود. در شکل زیر نیرو‌های وارد به جسم در دو حالتِ حرکت به سمت بالا و پایین، نشان داده شده‌اند.

از طرفی تغییرات تکانه نسبت به زمان، معادل با نیروی وارد به یک سیستم است. بنابراین معادلات دیفرانسیل حاکم بر جسم در هر یک از حالات به صورت زیر بدست می‌آیند.

$$\begin {align*} \begin{array} \large \begin{aligned}&\hspace{0.5in}{\mbox{Up}}\\ & mv ^ {\prime} = mg + 5{v^2}\\ & v ^ { \prime } = 9.8 + \frac{1}{{10}}{v^2}\\ & v\left( 0 \right) = -10\end{aligned}&\begin{aligned}&\hspace{0.35in}{\mbox{Down}}\\ & mv ^ {\prime} = m g – 5 { v ^ 2 } \\ & v ^ { \prime } = 9.8 – \frac { 1 }{ { 1 0 } }{ v ^ 2 } \\ & v\left( { { t _ 0} } \right) = 0\end {aligned}\end{array} \end{align*}$$

همان‌طور که می‌بینید معادلات دیفرانسیل در دو حالت حرکت به سمت بالا و پایین نسبت به یکدیگر متفاوت هستند. بنابراین نمی‌توان تنها با استفاده از یکی از معادلات فوق، کل پدیده را مدل‌سازی کرد. در ابتدا معادلاتِ حرکت به سمت بالا را به صورت زیر بدست می‌آوریم.

$$\begin{align*} \large \int{{\frac{1}{{9.8 + \frac{1}{{10}}{v^2}}}\,dv}} & = \int{{ d t } }\\ 10\int{{\frac{1}{{98 + { v^ 2 } } } \, d v } } & = \int { { d t} } \\ \frac { { 10 } } { { \sqrt {98} }}{\tan ^{ - 1 } } \left ( { \frac { v } { { \sqrt {98} } } } \right) & = t + c\end{align*} $$

بنابراین نهایتا رابطه مربوط به سرعت جسم در حرکت بالارونده مطابق با رابطه فوق بدست می‌آید. توجه داشته باشید که جهت مثبت محور $$y$$ به سمت پایین در نظر گرفته شده، به همین دلیل سرعت اولیه برابر با $$\begin{align*} v\left( 0 \right) = - 10 \end{align*} $$ در نظر گرفته شده است. با استفاده از این مقدار و به صورت زیر می‌توان مقدار $$c$$ را بدست آورد.

$$\begin{align*} c = \frac { { 10 } } { { \sqrt {98} } } { \tan ^ { - 1 } } \left ( { \frac { { - 10} } { { \sqrt {98} }}} \right) \end{align*} $$

بنابراین نهایتا رابطه مربوط به سرعت جسم در هنگام حرکت رو به بالا به صورت زیر بدست می‌آید.

$$\begin{align*} \large \frac { { 10 } } { { \sqrt {98} } } { \tan ^{ - 1}}\left( {\frac{v}{{\sqrt {98} }}} \right) & = t + \frac { { 10 } } { { \sqrt {98} } } { \tan ^{ - 1}}\left( {\frac{{ - 10}}{{\sqrt {98} }}} \right) \\ {\tan ^{ - 1}}\left( {\frac{v}{{\sqrt {98} }}} \right) & = \frac { { \sqrt {98} } } { { 10}} t + {\tan ^{ - 1}}\left( {\frac{{ - 10}}{{\sqrt {98} }}} \right) \\~\\ v\left( t \right) & = \sqrt {98} \tan \left( {\frac{{\sqrt {98} } } { {10 } } t + { {\tan } ^ { - 1} } \left( {\frac{{ - 10 } } { { \sqrt {98} } } } \right)} \right)\end{align*}$$

حال باید زمانی را بدست آوریم که در آن جسم به بیشترین ارتفاعش می‌رسد. بدین منظور رابطه مربوط به سرعت را برابر با صفر قرار می‌دهیم. بنابراین با صفر قرار دادن رابطه فوق، زمانی که جسم در اوج حرکتش است، برابر با عدد زیر بدست می‌آید (اثبات این قسمت را به خودتان می‌سپاریم).

$$\begin{align*} \large t = \frac { { 10 } } { { \sqrt {98} } } \left [ { { { \tan } ^ { - 1 } } \left( {\frac{{10}}{{\sqrt {98} } } } \right) + \pi n} \right]\hspace{0.25in}n = 0, \pm 1, \pm 2, \pm 3, \ldots \end {align*}$$

بدیهی است که تمامی مقادیر بدست آمده در بالا نیاز نبوده و تنها کوچک‌ترین مقدار مثبت را می‌توان به عنوان پاسخ نهایی در نظر گرفت. نهایتا زمان اوج جسم برابر با $$\begin{align*} t = 0.79847 \end{align*}$$ بدست می‌آید. بنابراین معادله مقدار اولیه را می‌توان به صورت زیر بیان کرد:

$$\begin{align*} \large v ^ { \prime } = 9.8 - \frac{1}{{10}}{v^2}\hspace{0.25in} , \ \ v \left( {0.79847} \right ) = 0 \end{align*} $$

در ابتدا با جداسازی معادله و انتگرال‌گیری از آن داریم:

$$\begin{align*} \large \int { { \frac { 1 }{{9.8 - \frac{1}{{10}} { v ^ 2 }} } \, d v } } = 10\int{{\frac{1}{{98 - { v ^ 2 } } } \, d v }} = \int{{ d t } } \end{align*} $$

در مطلب انتگرال‌گیری به روش‌ کسر‌های جزئی نحوه محاسبه انتگرال چنین توابعی را توضیح دادیم. البته در روش انتگرال به روش تغییر متغیر مثلثاتی نیز روش‌ حل انتگرال این گونه توابع را توضیح داده‌ایم. نهایتا با استفاده از تجزیه عبارت تحت انتگرال به صورت $$\begin{align*} 98 - { v ^ 2 } = \left ( { \sqrt {98} - v } \right ) \left( {\sqrt { 98 } + v } \right) \end{align*} $$، می‌توان کسر را ساده‌تر کرده و انتگرال را به صورت زیر بدست آورد.

$$ \large \begin{align*}10\left( {\frac { 1 } { { 2\sqrt {98} } } } \right)\int{{\frac{1 } { { \sqrt {98} + v } } + \frac { 1 } { { \sqrt {98} - v}}\,dv}} & = \int {{ d t } } \\ \frac{5}{{\sqrt { 98 } } } \left[ {\ln \left| { \sqrt {98} + v} \right| - \ln \left| {\sqrt {98} - v } \right| } \right] & = t + c \\ \frac { 5 }{ { \sqrt {98} } } \ln \left| {\frac { { \sqrt {98} + v } } { { \sqrt {98} - v} } } \right| & = t + c \end{align*} $$

فیلم مجموعه آموزش ریاضیات – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

در حالتی که جسم به سمت پایین حرکت می‌کند نیز همانند حالت بالارونده، با اعمال شرایط اولیه، مقدار ثابتِ $$c$$ بدست خواهد آمد.

$$ \large \begin {align*} \frac { 5 } { { \sqrt {98} } } \ln \left| {\frac{{\sqrt {98} + v \left( {0.79847 } \right ) } } { { \sqrt {98} - v(0.79847}}} \right| & = 0.79847 + c\\ \frac { 5 } { { \sqrt { 98 } } } \ln \left| { \frac { { \sqrt {98} + 0 } } { { \sqrt { 98 } - 0 } } } \right| & = 0.79847 + c \\ \frac { 5 } { { \sqrt {98} } } \ln \left| 1 \right| & = 0.79847 + c\\ c & = - 0.79847\end{align*} $$

نهایتا رابطه توصیف کننده سرعت در هنگام پایین آمدن جسم برابر می‌شود با:

$$ \large \begin {align*} \frac { 5 } { { \sqrt { 98 } } } \ln \left| { \frac { { \sqrt {98} + v } }{ { \sqrt {98} - v } } } \right| = t - 0.79847 \end{align*} $$

رابطه فوق را می‌توان به صورت زیر نیز بازنویسی کرد.

$$ v \left( t \right) = \large \sqrt {98} \frac { { { { { e } } ^ {\frac { 1 } { 5 } \sqrt {98} \left( {t - 0.79847} \right ) } } - 1 } } { { { {{ e } } ^ { \frac { 1 } {5 } \sqrt {98} \left( {t - 0.79847} \right ) } } + 1}}$$

بنابراین نهایتا رابطه کلی توصیف کننده حرکتِ جسم را می‌توان به صورت زیر بیان کرد:

$$ \large v \left ( t \right ) = \left \{ { \begin {array} {ll}{\sqrt {98} \tan \left( {\frac { { \sqrt {98} } } { {10 } } t + {{\tan }^{ - 1}}\left( {\frac{{ - 10 } } { { \sqrt {98} } } } \right)} \right ) } & { 0 \le t \le 0.79847\, \, \, \left( { { \mbox{upward motion}}} \right ) } \\ { \sqrt {98} \frac { { { { \bf { e } } ^ {\LARGE { \frac { 1 } {5 } \sqrt {98} \left( {t - 0.79847} \right)}}} - 1} } { { {{ \bf { e } } ^ { \LARGE { \frac { 1} { 5 } \sqrt {98} \left ( {t - 0.79847} \right) } } } + 1 } } } & { 0.79847 \le t \le { t _ { { \mathop{\rm end} \nolimits} } } \, \, \left ( {{\mbox{downward motion} } } \right)}\end{array}} \right. $$

توجه داشته باشید که $$ {t_{{\mbox{end}}}} $$ نشان دهنده زمانی است که جسم به زمین برخورد می‌کند. توجه داشته باشید که همانند دو مثال مطرح شده، برای اکثر پدیده‌های فیزیکی معادله‌ای وجود دارد که برای برخی از آن‌ها پاسخ‌های تحلیلی نیز وجود دارد. برای نمونه معادله‌ای در مکانیک سیالات وجود دارد که می‌توان با استفاده از آن مسیر حرکت دود سیگار را مدل‌سازی کرد! شاید برایتان جالب باشد اگر جست و جو کرده و با این معادله آشنا شوید.