مساحت انواع مثلث چگونه بدست می آید؟ — حل تمرین و مثال های متنوع

فرمول کلی برای محاسبه مساحت تمام مثلث‌ها، قاعده ضربدر ارتفاع تقسیم بر دو است. البته فرمول هرون و روابط مثلثاتی نیز در حالت‌های مختلف، به منظور محاسبه مساحت مثلث مورد استفاده قرار می‌گیرند. با این وجود، برخی از انواع مثلث مانند مثلث‌های قائم الزاویه، متساوی الساقین و متساوی الاضلاع، از ویژگی‌های متفاوتی برخوردار هستند. در این مثلث‌ها، علاوه بر فرمول‌های کلی، امکان به کارگیری فرمول‌‌های اختصاصی نیز وجود دارد. در این مقاله از مجله فرادرس، به معرفی فرمول‌ها و نحوه محاسبه مساحت انواع مثلث به همراه حل چندین مثال می‌پردازیم.

مثلث چیست؟

مثلث، یکی از شکل‌های هندسی پایه است که از سه راس، سه قاعده، سه زاویه داخلی، سه زاویه خارجی و سه ارتفاع تشکیل می‌شود.

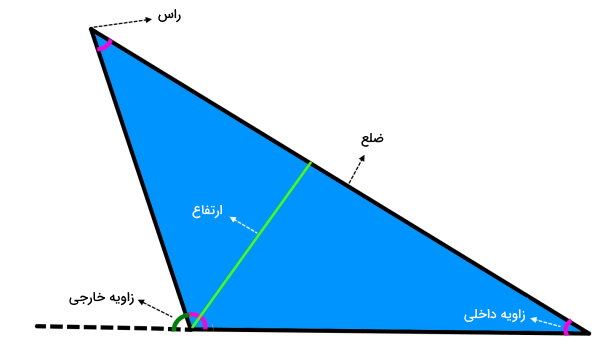
مساحت مثلث چیست؟

مساحت مثلث، اندازه سطح محدود به ضلع‌های این شکل هندسی است.

سطح درون اضلاع مثلث‌ها، با توجه به مقادیر اجزای آن‌ها، مخصوصا ارتفاع و قاعده تعیین می‌شود.

فرمول مساحت انواع مثلث چیست؟

مساحت مثلث، از ضرب قاعده در ارتفاع تقسیم بر 2 به دست می‌آید.

فرمول مساحت مثلث بر حسب قاعده و ارتفاع به صورت زیر نوشته می‌شود:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

$$A = \frac {h \times b } { 2 }$$

• A: مساحت
• h: ارتفاع
• b: قاعده

در صورت معلوم بودن اندازه تمام اضلاع، فرمول مساحت مثلث با سه ضلع (فرمول هرون) مورد استفاده قرار می‌گیرد:

$$A = \sqrt { s ( s - a ) ( s - b ) ( s- c ) }$$

• A: مساحت
• s: نصف محیط مثلث
• a: طول ضلع اول
• b: طول ضلع دوم
• c: طول ضلع سوم

اگر اندازه یک ضلع و دو زاویه یا یک زاویه و دو ضلع از مثلث معلوم باشد، می‌توان از فرمول مساحت مثلث با سینوس استفاده کرد:

$$Area=\frac{1}{2} a b \sin A$$

$$\text { Area }=\frac{c^{2} \sin A \sin B}{2 \sin C}$$

• Area: مساحت
• a: طول ضلع CB
• b: طول ضلع AC
• c: طول ضلع AB
• A: زاویه راس A
• B:‌زاویه راس B
• C: زاویه راس C

در آموزش‌های ریاضی پیشین از مجله فرادرس با محاسبه مساحت مثلث آشنا شدیم. سه روش معرفی شده، فرمول‌های مساحت برای تمام مثلث‌ها هستند. برای انواع مثلث با ویژگی‌های منحصر به فرد (زاویه قائمه یا ضلع‌های برابر)، معمولا از فرمول‌های مخصوص استفاده می‌شود.

مثال: محاسبه مساحت مثلث به سه روش کلی

مساحت سه مثلث نمایش داده شده در تصویر زیر را حساب کنید.

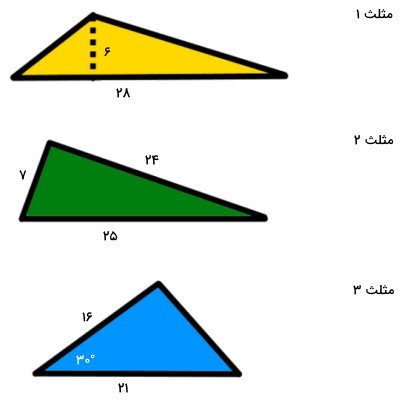
برای مثلث شماره 1، اندازه‌های قاعده و ارتفاع نظیر مثلث داده شده‌اند. بنابراین، فرمول مناسب برای محاسبه مساحت این مثلث، عبارت است از:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

$$A = \frac {h \times b } { 2 }$$

• A₁: مساحت مثلث شماره ۱
• b: قاعده برابر 28
• h: ارتفاع برابر 6

اندازه‌های معلوم را درون فرمول قرار می‌هیم و مقدار مساحت مثلث شماره 1 را محاسبه می‌کنیم:

$$A = \frac {6 \times 28 } { 2 }$$

$$A = 3 \times 28$$

$$A = 84$$

مساحت مثلث شماره 1 برابر 84 است. در ادامه، مساحت مثلث شماره 2 را به دست می‌آوریم. اندازه‌های هر سه ضلع این مثلث معلوم و متفاوت هستند. در نتیجه، استفاده از فرمول هرون، بهترین گزینه برای محاسبه مساحت است. این فرمول را به همراه اندازه هر ضلع یادداشت می‌کنیم:

$$A = \sqrt { s ( s - a )( s - b ) ( s - c ) }$$

• A₂: مساحت مثلث شماره ۲
• a: اندازه ضلع a برابر 7
• b: اندازه ضلع b برابر 25
• c: اندازه ضلع c برابر 24

نصف محیط مثلث، عبارت است از:

$$s = \frac { 7 + 25 + 24 } { 2 }$$

$$s=\frac{56}{2}$$

$$s=28$$

نصف محیط را به همراه دیگر اندازه‌های معلوم، درون فرمول هرون قرار می‌هیم:

$$A = \sqrt { 28 ( 28 - 7 )( 28 - 25 ) ( 28 - 24 ) }$$

$$A = \sqrt { 28 ( 21 )( 3 ) ( 4 ) }$$

$$A = \sqrt { 7056 }$$

$$A = 84$$

مساحت مثلث شماره ۲ نیز برابر 84 است. همان طور که مشاهده می‌کنید، با وجود اندازه‌های متفاوت، مساحت‌های دو مثلث 1 و 2 برابر هستند. در مثلث سوم، اندازه دو ضلع و زاویه بین آن‌ها داده شده است. برای محاسبه مساحت این مثلث، فرمول زیر را می‌نویسیم:

$$A=\frac{1}{2} a \cdot b \cdot sin C$$

• A₃: مساحت مثلث شماره ۳
• a: اندازه ضلع اول برابر 16
• b: اندازه ضلع دوم برابر 21
• C: زاویه بین اضلاع اول و دوم برابر 30 درجه

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم:

$$A=\frac{1}{2} \times 16 \times 21 \times \sin 30°$$

$$A = 8 \times 21 \times 0.5$$

$$A = 4 \times 21$$

$$A = 84$$

مساحت مثلث شماره ۳ نیز مانند مثلث‌های ۱ و ۲ برابر 84 است. به منظور محاسبه مساحت برای مثلث‌های معرفی شده در این مثال، تمام اندازه‌های مورد نیاز داده شده بود. اگر حتی یکی از این اندازه‌ها مشخص نبود، امکان تعیین مساحت وجود نداشت. با این وجود، در مثلث‌های خاص، نیازی به دانستن تمام انداز‌ه‌ها نیست. به عنوان مثال، مساحت مثلث متساوی الاضلاع، فقط با داشتن اندازه یکی از ضلع‌ها یا اندازه یکی از ارتفاع‌ها به دست می‌آید.

انواع مثلث چه هستند؟

مثلث‌ها، بر اساس اندازه زوایای داخلی و اضلاع، به انواع حاده، قائم الزاویه، منفرجه، مختلف الاضلاع، متساوی الساقین و متساوی الاضلاع تقسیم می‌شوند.

• انواع مثلث بر اساس اندازه زوایای داخلی
  • مثلث حاده (با زاویه بسته)
  • مثلث قائم الزاویه (با زاویه 90 درجه)
  • مثلث منفرجه (با زاویه باز)
• انواع مثلث بر اساس اندازه اضلاع
  • مثلث مختلف الاضلاع (بدون ضلع هم اندازه)
  • مثلث متساوی الساقین (دو ضلع هم اندازه)
  • مثلث متساوی الاضلاع (سه ضلع هم اندازه)

از بین موارد بالا، مثلث‌های قائم الزاویه، متساوی الساقین و متساوی الاضلاع، معمولا با استفاده از فرمول‌های مخصوص به خود محاسبه می‌شوند. در بخش‌های بعدی، به معرفی فرمول‌های این مثلث‌ها و حل مثال‌های مربوط به آن‌ها می‌پردازیم.

مثلث قائم الزاویه چیست و مساحت آن چگونه بدست می آید ؟

مثلث قائم الزاویه، مثلثی با یک زاویه راست یا 90 درجه است. ضلع‌های تشکیل دهنده زاویه راست، با عنوان «ساق» و ضلع مقابل این زاویه، با عنوان «وتر» شناخته می‌شوند. ساق‌ها، ارتفاع و قاعده نظیر یکدیگر هستند.

به این ترتیب، در صورت مشخص بودن اندازه این دو ضلع، مساحت مثلث، توسط فرمول «قاعده ضربدر ارتفاع تقسیم بر دو» به دست می‌آید. علاوه بر این، اگر اندازه یکی از ساق‌ها و وتر در این مثلث مشخص باشد، امکان تعیین مساحت با استفاده از فرمول مخصوص و بدون نیاز به ارتفاع وجود دارد.

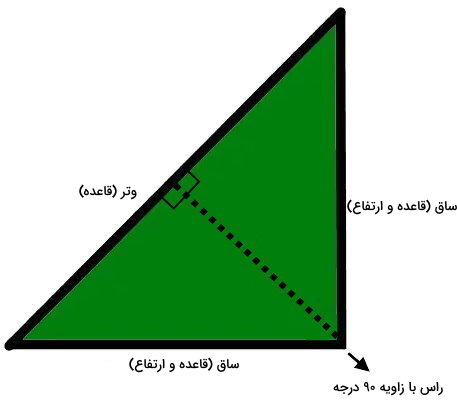
مثلث قائم الزاویه از قضیه فیثاغورس پیروی می‌کند. فرم ریاضی این قضیه عبارت است از:

$$c^ { 2 } = a^ { 2 } + b^ {2}$$

• c: وتر مثلث قائم الزاویه
• a: یکی از ساق‌های مثلث
• b: ساق دیگر مثلث

بر اساس رابطه بالا، فرمول مخصوص مثلث قائم الزاویه، به صورت زیر نوشته می‌شود:

$$A = \frac { a \sqrt { c^{ 2 } - a^{ 2 }} } {2}$$

• c: وتر
• a: یکی از ساق‌ها

توجه داشته باشید که در صورت داشتن اندازه دو ضلع مثلث قائم الزاویه، می‌توان اندازه ضلع سوم را توسط قضیه فیثاغورس به دست آورد و مساحت مثلث را به کمک فرمول هرون محاسبه کرد. فرمول مخصوص مثلث قائم الزاویه، هنگام مشخص بودن وتر و یکی از ساق‌ها کاربرد دارد.

مثال: محاسبه مساحت مثلث قائم الزاویه با دو ضلع

مساحت مثلث قائم الزاویه با وتر 13 سانتی‌متر و ساق 5 سانتی‌متر را محاسبه کنید.

به دلیل مشخص بودن اندازه وتر و یکی از ساق‌ها، می‌توانیم از فرمول مخصوص مثلث قائم الزاویه استفاده کنیم. برای شروع محاسبات، این فرمول را به همراه اطلاعات مسئله می‌نویسیم:

$$A = \frac { a \sqrt { c^{ 2 } - a^{ 2 }} } {2}$$

• c: اندازه وتر مثلث برابر 13 سانتی‌متر
• a: اندازه یکی از ساق‌ها برابر 5 سانتی‌متر

اندازه‌ها را درون فرمول قرار می‌دهیم:

$$A = \frac { 5 \sqrt { 13^{ 2 } - 5^{ 2 }} } {2}$$

$$A = \frac { 5 \sqrt { 169 - 25} } {2}$$

$$A = \frac { 5 \sqrt { 144} } {2}$$

$$A = \frac { 5 \times 12} {2}$$

$$A = 5 \times 6$$

$$A = 30$$

مساحت مثلث برابر 30 سانتی‌متر مربع است. برای اطمینان از نتیجه، مساحت مثلث را توسط روش‌های دیگر محاسبه کنید. در بخش مثال‌ها، مساحت این مثلث را به روش‌های مختلف تعیین می‌کنیم.

مثلث متساوی الساقین چیست و مساحت آن چگونه بدست می آید ؟

مثلث متساوی الساقین، یکی دیگر از حالت‌های خاص مثلث با دو ضلع برابر است.

ضلع‌های هم اندازه در این مثلث، با عنوان «ساق» شناخته می‌شوند. به ضلع سوم مثلث متساوی الساقین، «قاعده» می‌گویند.

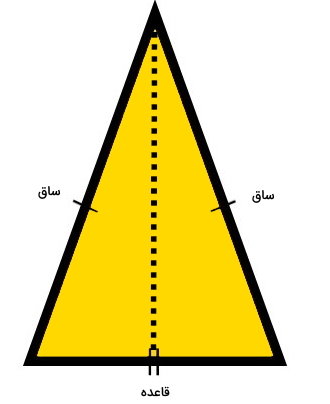
در صورت رسم ارتفاع نظیر قاعده در مثلث بالا، دو مثلث قائم الزاویه به وجود می‌آید. به این ترتیب، با کمک قضیه فیثاغورس، می‌توان فرمول مخصوص مساحت متساوی الساقین را بر اساس اندازه ساق و قاعده به دست آورد. این فرمول، به صورت زیر نوشته می‌شود:

$$A = \frac {1} {2} b \sqrt {a^2 -(\frac {b} {2})^2}$$

• A: مساحت
• a: اندازه ساق
• b: اندازه قاعده

مثال: محاسبه مساحت انواع مثلث متساوی الساقین با دو ضلع

مساحت مثلث متساوی الساقین با اندازه ساق 6 و قاعده 4 را به دست آورید.

مطابق با فرمول مخصوص مساحت متساوی الساقین بر اساس قاعده و ساق، داریم:

$$A = \frac {1} {2} b \sqrt {a^2 -(\frac {b} {2})^2}$$

• A: مساحت
• a: اندازه ساق برابر 6
• b: اندازه قاعده برابر 4

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم:

$$A = \frac {1} {2} \times 4 \times \sqrt {6^2 -(\frac {4} {2})^2}$$

$$A = 2 \times \sqrt {6^2 -(2)^2}$$

$$A = 2 \times \sqrt {36 -4}$$

$$A = 2 \times \sqrt {32}$$

$$A = 2 \times \sqrt {16 \times 2}$$

$$A = 2 \times 4 \sqrt {2}$$

$$A = 8 \sqrt {2}$$

مساحت مثلث برابر $$8 \sqrt {2}$$ است.

مثلث متساوی الساقین قائم الزاویه چیست و مساحت آن چگونه بدست می آید ؟

اگر زاویه بین دو ساق مثلث متساوی الساقین برابر 90 درجه باشد، مثلث از نوع متساوی الساقین قائم الزاویه خواهد بود. در این مثلث خاص، امکان محاسبه مساحت با استفاده از یکی از اضلاع (ساق و یا وتر) وجود دارد.

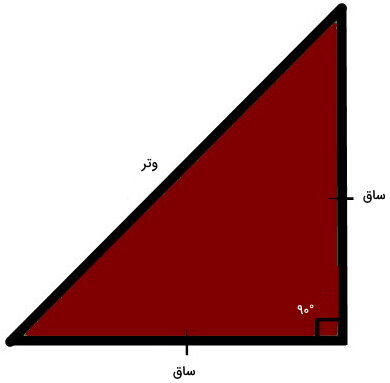
فرمول‌های مخصوص مثلث متساوی الساقین قائم الزاویه عبارت هستند از:

$$A=\frac{ a^ {2} }{2}$$

• a: ساق مثلث

$$A=\frac{ c^ {2} }{4}$$

• c: وتر مثلث

مثال: محاسبه مساحت انواع مثلث قائم الزاویه با یک ضلع

مساحت مثلث متساوی الساقین قائم الزاویه با وتر 7 متر را محاسبه کنید.

به دلیل قائم الزاویه بودن مثلث متساوی الساقین، دانستن اندازه یکی از ضلع‌های آن برای محاسبه مساحت کفایت می‌کند. فرمول مساحت این مثلث بر اساس اندازه وتر، به صورت زیر نوشته می‌شود:

$$A=\frac{ c^ {2} }{4}$$

$$A=\frac{ 7^ {2} }{4}$$

$$A=\frac{ 49 }{4}$$

$$A=12.25$$

مساحت مثلث برابر 12.25 متر مربع است.

مثلث متساوی الاضلاع چیست و مساحت آن چگونه بدست می آید ؟

مثلث متساوی الاضلاع، مثلثی با سه ضلع برابر است. علاوه بر اضلاع (قاعده‌ها)، اجزای دیگر این مثلث مانند زوایای داخلی و ارتفاع‌ها نیز دارای اندازه‌های یکسان هستند.

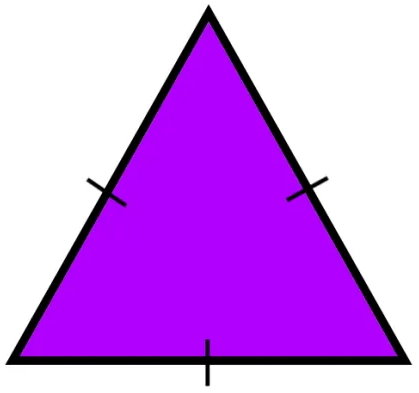
به دلیل هم اندازه بودن قاعده‌ها و ارتفاع‌های مثلث متساوی الاضلاع، فرمول‌های محاسبه مساحت انواع مثلث، در این حالت خاص، ساده‌سازی می‌شوند. فرمول‌های مخصوص مساحت مثلث متساوی الاضلاع عبارت هستند از:

$$A=\frac{\sqrt{3}}{4} a^{2}$$

• a: اندازه ضلع

$$A=\frac{\sqrt{3}}{3} h^{2}$$

• h: اندازه ارتفاع

بر اساس فرمول‌های بالا، در صورت داشتن یکی از اندازه‌های ضلع یا ارتفاع مثلث متساوی الاضلاع، می‌توان مساحت این نوع مثلث را به دست آورد.

مثال: محاسبه مساحت انواع مثلث متساوی الاضلاع با یک ضلع

مساحت مثلث متساوی الاضلاع با قاعده 5 چقدر است؟

از آنجایی که در صورت سوال، فقط به قاعده مثلث اشاره شده است، فرمول مخصوص مساحت مثلث متساوی الاضلاع بر اساس اندازه ضلع را می‌نویسیم:

$$A=\frac{\sqrt{3}}{4} a^{2}$$

• a: اندازه ضلع مثلث برابر 5

$$A=\frac{\sqrt{3}}{4} 5^{2}$$

$$A=\frac{\sqrt{3}}{4} \times 25$$

$$A=6.25\sqrt{3}$$

مساحت مثلث برابر $$6.25\sqrt{3}$$ است.

مثلث با زاویه باز چیست و مساحت آن چگونه بدست می آید ؟

مثلث با زاویه باز یا مثلث منفرجه، مثلثی است که یک زاویه بزرگ‌تر از 90 درجه دارد. ویژگی متفاوت این مثلث نسبت به انواع دیگر مثلث‌ها، قرارگیری دو ارتفاع آن در خارج از محدوده اضلاع است.

محاسبه مساحت انواع مثلث منفرجه با استفاده از روش‌های کلی (روش قاعده و ارتفاع، روش هرون و روش سینوس) انجام می‌گیرد.

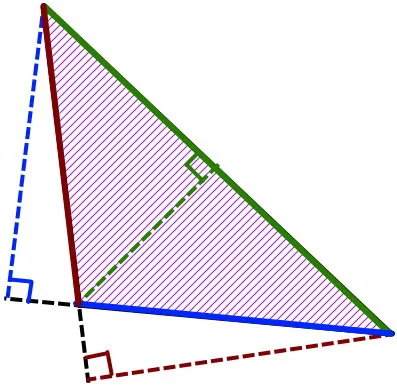
در صورت استفاده از روش قاعده و ارتفاع، باید توجه داشت که بخش بیرونی امتداد قاعده (از راس تا محل تقاطع با ارتفاع)، به عنوان اندازه قاعده در نظر گرفته نمی‌شود.

مثال های مساحت انواع مثلث

در این بخش، به حل چهار مثال متنوع در زمینه محاسبه مساحت انواع مثلث می‌پردازیم. علاوه بر فرمول‌های معرفی شده در بخش‌های قبلی، روابط کلی مساحت مثلث را نیز مورد بررسی و مقایسه قرار می‌دهیم.

مثال اول: تعیین مساحت مثلث و اجزای آن

مثلث زیر را در نظر بگیرید. مساحت این مثلث را به سه روش تعیین کنید. سپس، اندازه هر سه ارتفاع آن را به دست بیاورید.

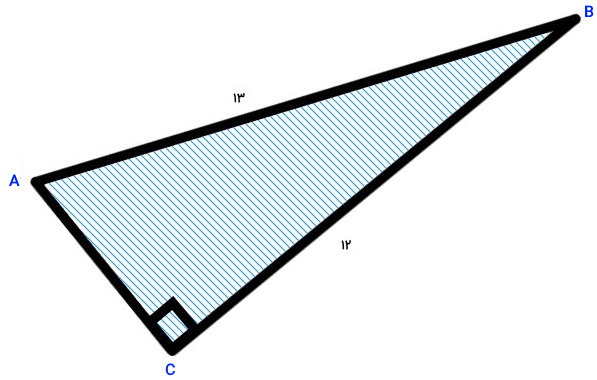
همان طور که مشاهده می‌کنید، مثلث بالا در راس C، یک زاویه 90 درجه دارد. بنابراین، این مثلث از نوع قائم الزاویه است. به این ترتیب، ضلع مقابل راس 90 درجه به عنوان وتر و دو ضلع دیگر به عنوان ساق در نظر گرفته می‌شوند.

روش اول: فرمول مساحت مثلث قائم الزاویه با وتر و یک ساق

به دلیل مشخص بودن اندازه وتر و یکی از ساق‌ها، مقدار مساحت مثلث، از فرمول زیر به دست می‌آید:

$$A = \frac { b \sqrt { c^{ 2 } - b^{ 2 }} } {2}$$

• c: اندازه وتر مثلث برابر 13
• b: اندازه ساق مقابل راس B برابر 12

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم:

$$A = \frac { 12 \sqrt { 13^{ 2 } - 12^{ 2 }} } {2}$$

$$A = \frac { 12 \sqrt { 169 - 144} } {2}$$

$$A = \frac { 12 \sqrt { 25} } {2}$$

$$A = \frac { 12 \times 5} {2}$$

$$A = 6 \times 5$$

$$A = 30$$

مساحت مثلث برابر 30 است.

روش دوم: فرمول مساحت مثلث قائم الزویه با دو ساق

وتر و یکی از ساق‌های مثلث مشخص هستند. با استفاده از قضیه فیثاغورس، اندازه ساق دوم را تعیین می‌کنیم. قضیه فیثاغورس برای مثلث مورد سوال عبارت است از:

$$c^ { 2 } = a^ { 2 } + b^ {2}$$

• c: اندازه وتر برابر 13 سانتی‌متر
• a: اندازه ساق مقابل راس A
• b: اندازه ساق مقابل راس B برابر 12 سانتی‌متر

اندازه‌های معلوم را درون رابطه بالا قرار می‌دهیم:

$$13^ { 2 } = a^ { 2 } + 12^ {2}$$

$$169 = a^ { 2 } + 144$$

$$169 - 144 = a^ { 2 }$$

$$25 = a^ { 2 }$$

$$\sqrt {25} = a$$

$$5 = a$$

اندازه دیگر ساق مثلث برابر 5 است. از آنجایی که در مثلث‌های قائم الزاویه، ساق‌ها، ارتفاع و قاعده نظیر یکدیگر هستند، می‌توان از فرمول کلی زیر برای محاسبه مساحت آن‌ها استفاده کرد:

$$A = \frac {h \times b } { 2 }$$

• A: مساحت
• h: ارتفاع
• b: قاعده

فرمول بالا را به شکل زیر بازنویسی می‌کنیم:

$$A = \frac {a \times b } { 2 }$$

• A: مساحت
• a: اندازه یکی از ساق‌ها برابر 5
• b: اندازه ساق دیگر برابر 12

با قرار دادن اندازه‌های معلوم در فرمول بالا، داریم:

$$A = \frac {5 \times 12 } { 2 }$$

$$A = 6 \times 5$$

$$A = 30$$

با استفاده از این روش نیز به مساحت 30 رسیدیم.

روش سوم: فرمول مساحت مثلث قائم الزاویه با سه ضلع

در روش قبلی، نحوه محاسبه ضلع سوم مثلث قائم الزاویه توسط قضیه فیثاغورس را توضیح دادیم. در صورت مشخص بودن اندازه هر سه ضلع مثلث، مساحت آن از طریق رابطه زیر (فرمول هرون) به دست می‌آید:

$$A=\sqrt{s(s-a)(s-b)(s-c)}$$

• A: مساحت
• s: نصف محیط مثلث
• a: اندازه ضلع اول برابر 5
• b: اندازه ضلع دوم برابر 12
• c: اندازه ضلع سوم برابر 13

نصف محیط مثلث، از رابطه زیر محاسبه می‌شود:

$$s=\frac{a+b+c}{2}$$

$$s=\frac{5+12+13}{2}$$

$$s=\frac{30}{2}$$

$$s=15$$

نصف محیط مثلث را به همراه دیگر اندازه‌های معلوم در فرمول هرون قرار می‌دهیم:

$$A=\sqrt{15(15-5)(15-12)(15-13)}$$

$$A=\sqrt{15(10)(3)(2)}$$

$$A=\sqrt{15(60)}$$

$$A=\sqrt{900}$$

$$A=30$$

مساحت مثلث با این روش نیز برابر 30 به دست آمد. همان طور که مشاهده می‌کنید، روش‌های مختلفی برای محاسبه مساحت انواع مثلث وجود دارد. با به دست آوردن مقدار مساحت، می‌توانیم اجزای دیگر مثلث نظیر ارتفاع‌های آن را تعیین کنیم.

تعیین ارتفاع‌های مثلث قائم الزاویه

در مثلث قائم الزاویه، ساق‌ها، ارتفاع و قاعده نظیر یکدیگر هستند. به دلیل مشخص بودن اندازه ساق‌ها، نیازی به محاسبه آن‌ها در این بخش از مثال نداریم. به این ترتیب، فقط ارتفاع نظیر وتر مثلث برای محاسبه باقی می‌ماند:

• h_a: ارتفاع نظیر ساق 5 برابر 12
• h_b: ارتفاع نظیر ساق 12 برابر 5
• h_c: ارتفاع نظیر وتر

بر اساس فرمول کلی مساحت مثلث، داریم:

$$A = \frac {c \times h_c } { 2 }$$

• A: مساحت مثلث برابر 30
• c: وتر (قاعده) برابر 13
• h_c: ارتفاع نظیر وتر

با قرار دادن اندازه‌های معلوم و حل فرمول بالا، ارتفاع نظیر وتر به دست می‌آید:

$$30 = \frac {13 \times h_c } { 2 }$$

$$30 \times 2 = 13 \times h_c$$

$$60 = 13 \times h_c$$

$$\frac {60} {13} = h_c$$

$$4.61 = h_c$$

ارتفاع نظیر وتر، برابر 4.61 است.

مثال دوم: محاسبه مساحت

مساحت مثلث زیر را به روش دلخواه محاسبه کنید. مساحت به دست آمده را با روش سینوس تایید کنید.

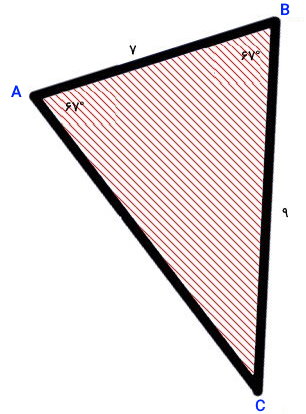
به دلیل برابر بودن زوایای دو راس A و B. مثلث بالا به عنوان یک مثلث متساوی الساقین در نظر گرفته می‌شود. بنابراین، دو ضلع BC و AC نیز هم اندازه هستند. پیش از شروع حل مسئله، اطلاعات موجود را یادداشت می‌کنیم:

• A: زاویه راس A برابر 67 درجه
• B: زاویه راس B برابر 67 درجه
• C: زاویه راس C برابر 46 درجه (جمع زوایای داخلی مثلث برابر 180 درجه است.)
• AB: اندازه قاعده AB برابر 7
• BC: اندازه ساق BC برابر 9
• AC: اندازه ساق AC برابر 9

اندازه‌های تمام اضلاع و زوایای مثلث ABC مشخص هستند. اکنون می‌توانیم با استفاده از روش دلخواه، مساحت آن را به دست بیاوریم. فرمول مخصوص مساحت انواع مثلث متساوی الساقین را می‌نویسیم:

$$A = \frac {1} {2} b \sqrt {a^2 -(\frac {b} {2})^2}$$

• A: مساحت
• a: اندازه ساق برابر 9
• b: اندازه قاعده برابر 7

$$A = \frac {1} {2} \times 7 \times \sqrt {9^2 -(\frac {7} {2})^2}$$

$$A = \frac {7} {2} \sqrt {81 -\frac {49} {4}}$$

$$A = \frac {7} {2} \sqrt {\frac {(4\times81)-49} {4}}$$

$$A = \frac {7} {2} \times \frac{\sqrt {324-49}} {\sqrt {4}}$$

$$A = \frac {7} {2} \times \frac{\sqrt {275}} {2}$$

$$A = \frac {7 \times 16.58} {4}$$

$$A ≅ 29$$

مساحت مثلث تقریبا برابر 29 است. برای تایید این مقدار، مساحت مثلث را به روش سینوس (دو ضلع و زاویه بین) محاسبه می‌کنیم. فرمول مساحت انواع مثلث با سینوس، به صورت زیر نوشته می‌شود:

$$Area=\frac{1}{2} a b \sin C$$

• Area: مساحت
• a: طول ضلع CB برابر 9
• b: طول ضلع AC برابر 9
• C: زاویه راس C برابر 46 درجه

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم:

$$Area=\frac{1}{2} \times 9 \times 9 \times \sin 46°$$

سینوس زاویه 46 حدودا برابر 0.72 است. بنابراین:

$$Area=\frac{1}{2} \times 81 \times 0.72$$

$$Area=\frac{1}{2} \times 58.3$$

$$A ≅ 29$$

مثال سوم: محاسبه مساحت مثلث متساوی الساقین با یک ضلع

مساحت مثلث زیر را به سریع‌ترین روش ممکن محاسبه کنید.

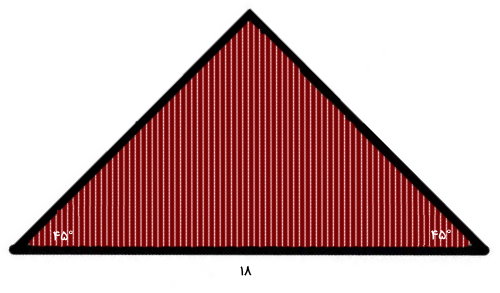
به دلیل وجود دو زاویه هم اندازه، مثلث بالا، به عنوان یک مثلث متساوی الساقین در نظر گرفته می‌شود. بر اساس اصل جمع زوایای داخلی، اندازه زاویه سوم این مثلث برابر 90 درجه خواهد بود. از این‌رو، مثلث بالا، یک مثلث متساوی الساقین قائم الزاویه است. برای شروع محاسبات، فرمول مخصوص محاسبه مساحت انواع مثلث متساوی الساقین قائم الزاویه را می‌نویسیم:

$$A=\frac{ c^ {2} }{4}$$

• c: اندازه وتر مثلث برابر 18

$$A=\frac{ 18^ {2} }{4}$$

$$A=\frac{ 324 }{4}$$

$$A=81$$

این مثال، با استفاده از روش محاسبه مساحت مثلث با دو زاویه و ضلع بین نیز قابل حل بود. با این وجود، آن روش به محاسبات بیشتر و پیچیده‌تری نیاز داشت.

مثال چهارم: مساحت قسمت رنگی مثلث

مساحت قسمت رنگی مثلث قائم الزاویه زیر را به دست آورید.

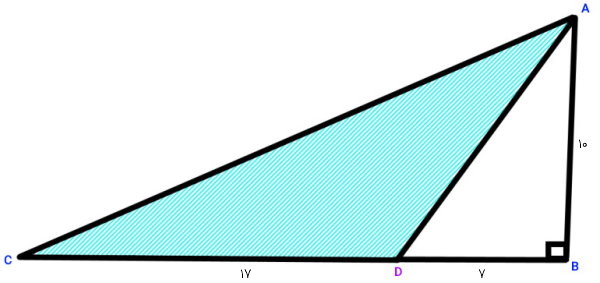
تصویر بالا از سه مثلث ABC (مثلث قائم الزاویه بزرگ)، ABD (مثلث قائم الزاویه کوچک) و ADC (مثلث منفرجه) تشکیل می‌شود. محاسبه مساحت بخش رنگی، با استفاده از دو روش قابل محاسبه است.

روش اول: تفریق مساحت دو مثلث قائم الزاویه

اولین روش برای محاسبه مساحت بخش رنگی کم کردن مساحت مثلث قائم الزاویه کوچک (ABD) از مساحت مثلث قائم الزاویه بزرگ (ABC) است. مساحت مثلث‌های قائم الزاویه از ضرب ساق‌ها تقسیم بر دو به دست می‌آید:

$$A = \frac {a \times b } { 2 }$$

• A: مساحت
• a: اندازه یکی از ساق‌ها
• b: اندازه ساق دیگر

مساحت بخش رنگی برابر است با:

مساحت مثلث ABD - مساحت مثلث ABC = مساحت بخش رنگی

مساحت مثلث ABC به صورت زیر محاسبه می‌شود:

$$A_{ABC} = \frac {a_{ABC} \times b_{ABC} } { 2 }$$

• A_ABC: مساحت
• a_ABC: اندازه ساق BC برابر 24 (جمع 17 و 7)
• b_ABC: اندازه ساق AB برابر 10

$$A_{ABC} = \frac {24 \times 10 } { 2 }$$

$$A_{ABC} = \frac {240 } { 2 }$$

$$A_{ABC} = 120$$

برای مثلث ABD، داریم:

$$A_{ABD} = \frac {a_{ABD} \times b_{ABD} } { 2 }$$

• A_ABD: مساحت
• a_ABD: اندازه ساق BD برابر 7
• b_ABD: اندازه ساق AB برابر 10

$$A_{ABD} = \frac {7 \times 10 } { 2 }$$

$$A_{ABD} = \frac {70 } { 2 }$$

$$A_{ABD} = 35$$

در نتیجه، مساحت قسمت رنگی، برابر است با:

$$A_{ABC}-A_{ABD}$$

$$120-35$$

$$85$$

مساحت بخش رنگی (مثلث ADC) برابر 85 است.

روش دوم: مساحت مثلث منفرجه

اگر به شکل مسئله دقت کنید، بخش رنگی (مثلث ADC) مانند یک مثلث منفرجه است. امتداد ضلع CD در این مثلث، در نقطه B به یکی از ساق‌های مثلث قائم الزاویه (ساق AB) برخورد کرده و یک زاویه 90 ساخته است. در واقع، ساق AB را می‌توان به عنوان ارتفاع نظیر قاعده CD در نظر گرفت. مطابق با فرمول کلی مساحت انواع مثلث داریم:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

$$A = \frac {h \times b } { 2 }$$

• A: مساحت
• h: اندازه ارتفاع برابر 10
• b: اندازه قاعده برابر 17

اندازه‌های قاعده و ارتفاع مثلث ADC را درون فرمول بالا قرار می‌گیریم:

$$A_{ADC} = \frac {AB \times CD } { 2 }$$

$$A_{ADC} = \frac {10 \times 17 } { 2 }$$

$$A_{ADC} = \frac {170 } { 2 }$$

$$A_{ADC} = 85$$

با استفاده از این روش نیز مقدار مساحت بخش رنگی، برابر با 85 به دست آمد.

سوالات متداول مساحت انواع مثلث

ذر این مطلب از مجله فرادرس فهمیدیم چگونه مساحت انواع مثلث‌ها را به‌دست آوریم. در این بخش، به برخی از سوالات پرتکرار در زمینه مساحت انواع مثلث پاسخ می‌دهیم.

مساحت انواع مثلث چگونه بدست می آید ؟

مساحت انواع مثلث، مخصوصا مثلث‌های مختلف الاضلاع، با استفاده از روش‌های کلی نظیر قاعده و ارتفاع، هرون و سینوس به دست می‌آید.

فرمول اصلی مساحت انواع مثلث چیست؟

شناخته شده‌ترین و رایج‌ترین فرمول مورد استفاده برای محاسبه مساحت انواع مثلث، «قاعده ضربدر ارتفاع تقسیم بر دو» است. این فرمول برای تمام مثلث‌ها قابل استفاده است.

چه اندازه‌هایی برای محاسبه مساحت انواع مثلث قائم الزاویه نیاز است؟

به منظور محاسبه مساحت انواع مثلث قائم الزاویه، دانستن اندازه یک ساق و وتر کفایت می‌کند.

آیا امکان محاسبه مساحت انواع مثلث با یک ضلع وجود دارد؟

از بین انواع مثلث، فقط امکان محاسبه مساحت مثلث‌های متساوی الاضلاع و متساوی الساقین قائم الزاویه با یک ضلع وجود دارد.