مبدل باک بوست (Buck–Boost) — به زبان ساده

در آموزش‌های پیشین مجله فرادرس، با مبدل‌های DC/DC نوع باک و بوست آشنا شدیم. دیدیم که مبدل باک یا کاهنده، ولتاژ‌ DC ورودی را به یک ولتاژ DC کوچکتر در خروجی کاهش می‌دهد. همچنین با مبدل بوست ولتاژ‌ DC ورودی را به یک ولتاژ DC بزرگتر در خروجی افزایش می‌دهد. در این آموزش، با مبدل باک بوست (Buck–Boost) آشنا می‌شویم. مدار این مبدل به گونه‌ای است که هم می‌تواند ولتاژ را افزایش و هم کاهش دهد.

مبدل باک بوست

مبدل‌های DC/DC به عنوان چاپر نیز شناخته می‌شوند. ویژگی بارز مبدل باک بوست این است که می‌تواند بسته به چرخه وظیفه $$D$$ به عنوان یک مبدل کاهنده یا یک مبدل افزاینده DC/DC کار کند.

فیلم آموزش الکترونیک صنعتی و مبدل ها در فرادرس

کلیک کنید

شکل زیر، مدار یک مبدل باک بوست را نشان می‌دهد.

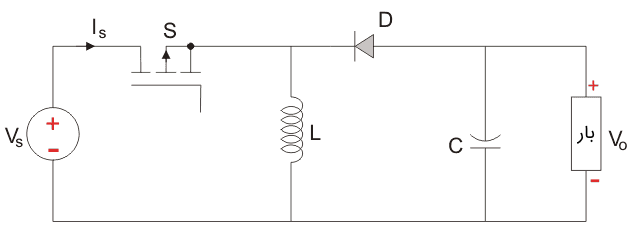
منبع ولتاژ ورودی به یک کلید حالت جامد وصل شده است. کلید دوم یک دیود است. دیود به صورت معکوس در جهت عبور توان از منبع به خازن و در نتیجه بار قرار گرفته است. همان‌طور که می‌بینیم، بار و خازن نیز با یکدیگر موازی هستند.

کلیدِ کنترل شده با استفاده از مدولاسیون پهنای پالس (PWM) روشن و خاموش می‌شود. مدولاسیون پهنای پالس می‌تواند مبتنی بر زمان یا فرکانس باشد. مدولاسیون مبتنی بر فرکانس معایبی از جمله محدوده گسترده فرکانس‌ها برای دستیابی به کنترل کلید برای رسیدن به ولتاژ خروجی مطلوب دارد. در مبدل‌های DC/DC اغلب از مدولاسیون مبتنی بر زمان استفاده می‌شود. پیاده‌سازی این مدولاسین ساده‌تر است. در این نوع مدولاسیون، فرکانس ثابت می‌ماند.

مدهای کاری مبدل باک بوست

مبدل باک بوست دو مد کاری دارد. مد اول وقتی اتفاق می‌افتد که کلید وصل بوده و جریان از آن عبور کند. مد دوم نیز در حالتی است که کلید قطع باشد. در ادامه، عملکرد مبدل را در این دو مد شرح می‌دهیم.

فیلم آموزش مدارهای الکتریکی ۱ در فرادرس

کلیک کنید

مد اول:‌ کلید وصل و دیود قطع

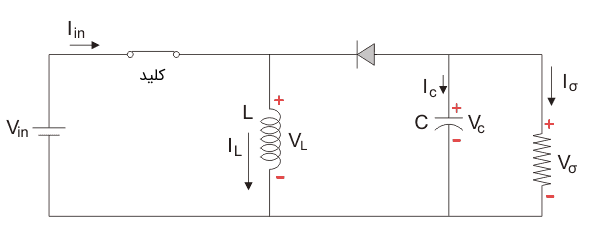
در این مد، کلید وصل بوده و به همین دلیل، همه جریان از آن عبور کرده و به سلف وارد می‌شود و پس از آن به منبع DC باز می‌گردد. در زمان وصل بودن سوئیچ، سلف انرژی ذخیره می‌کند و وقتی کلید قطع می‌شود، پلاریته آن معکوس شده و جریان این بار به بار منتقل شده و از طریق دیود به سلف بر می‌گردد. بنابراین، جهت جریان سلف تغییری نمی‌کند.

زمان وصل بودن کلید را $$ T _ {ON}$$ و زمان قطع بودن آن را $$ T_ {OFF}$$ در نظر می‌گیریم. دوره زمانی را $$T$$ تعریف می‌کنیم که برابر با $$ T = T_{ON}+T_{OFF}$$ است و فرکانس سوئیچینگ به صورت زیر خواهد بود:

$$ \large f _\text{switching} = \frac { 1 } { T} $$

چرخه وظیفه را به صورت زیر تعریف می‌کنیم:

$$ \large D = \frac {T_{ON}}{T}$$

حال، مبدل باک بوست را در حالت مانا برای این مد با استفاده از KVL تحلیل می‌کنیم. در این صورت، معادلات زیر را خواهیم داشت:

$$ \large
\therefore V _ { i n } = V _ { L } \\ \large
\therefore V _ { L } = L \frac { d i _ { L } } { d t } = V _{ i n } \\ \large \frac { d i _ { L } } { d t } = \frac { \Delta i _ { L } } { \Delta t } = \frac { \Delta i _ { L } } { D T } = \frac { V _ { i n } } { L } $$

از آنجایی که کلید به مدت $$ T_{ON} = D T $$ وصل است، می‌توان گفت که $$ \Delta t = D T $$ و داریم:

$$ \large (\Delta i _ L ) _{closed} = \left (\frac {V _{in}}{L} \right ) D T $$

هنگام تحلیل مبدل باک بوست باید به نکات زیر توجه کنیم:

1. جریان سلف پیوسته است و این موضوع را می‌توان با انتخاب مقدار صحیح $$L$$ تحقق بخشید.
2. جریان سلف در حالت مانا از یک مقدار با شیب مثبت شروع به افزایش می‌کند و به یک مقدار بیشینه در حالت وصل می‌رسد، سپس با یک شیب منفی به مقدار اولیه کاهش می‌یابد. بنابراین، تغییرات خالص جریان سلف در هر دوره کامل صفر است.

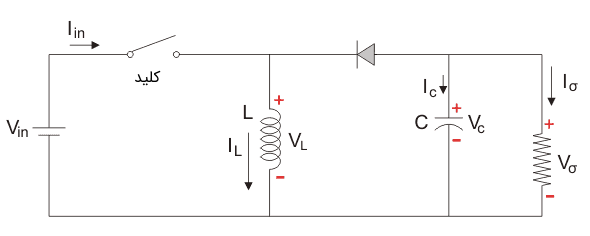
مد دوم: کلید قطع و دیود وصل

در این مد، پلاریته سلف معکوس شده و انرژی ذخیره شده در آن، در مقاومت بار تخلیه شده و این موضوع به برقراری جریان در یک جهت در بار و همچنین افزایش ولتاژ خروجی کمک می‌کند. دلیل این امر آن است که اکنون سلف مانند یک منبع عمل می‌کند.

حال مبدل باک بوست را در مد دوم با استفاده از KVL تحلیل می‌کنیم:

$$ \large \therefore V _ { L } = V _ { o } \\ \large
\therefore V _ { L } = L \frac { d i _ { L } } { d t } = V _ { o } \\
\large \frac { d i _ { L } } { d t } = \frac { \Delta i _ { L } }{ \Delta t } = \frac { \Delta i _ { L } } { ( 1 - D ) T } = \frac { V _ { o } } { L } $$

از آنجایی که کلید در زمان $$ T_ {OFF} = T - T_ {ON} = T - DT = (1- D)T$$ قطع است، خواهیم داشت: $$ \Delta t = ( 1 - D) T $$.

قبلاً گفتیم که تغییرات خالص جریان سلف در هر دوره برابر با صفر است:

$$ \large \therefore \left( \Delta i _ { L } \right ) _ { \text {closed}} + \left ( \Delta i _ { L } \right ) _ { \text {open}} = 0 \\ \large
\left( \frac { V _{ o } } { L } \right ) ( 1 - D ) T + \left ( \frac { V _ { \text {in}}} { L } \right ) D T = 0 \\ \large
\frac { V _ { o } } { V _ { \text {in}} } = \frac { - D } { 1 - D } $$

می‌دانیم که $$ D $$ بین ۰ و ۱ تغییر می‌کند. اگر $$ D > 0.5$$ باشد، آنگاه ولتاژ خروجی بزرگ‌تر از ولتاژ‌ ورودی خواهد بود و وقتی $$ D < 0.5$$ باشد، خروجی کوچک‌تر از ورودی است. اما اگر $$ D = 0.5 $$ باشد، ولتاژ خروجی برابر با ولتاژ ورودی است.

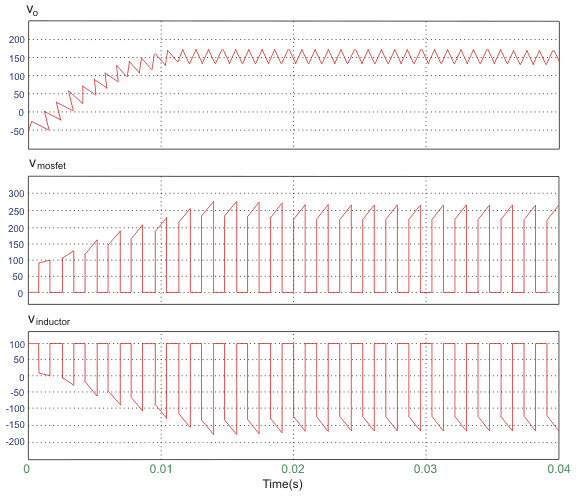
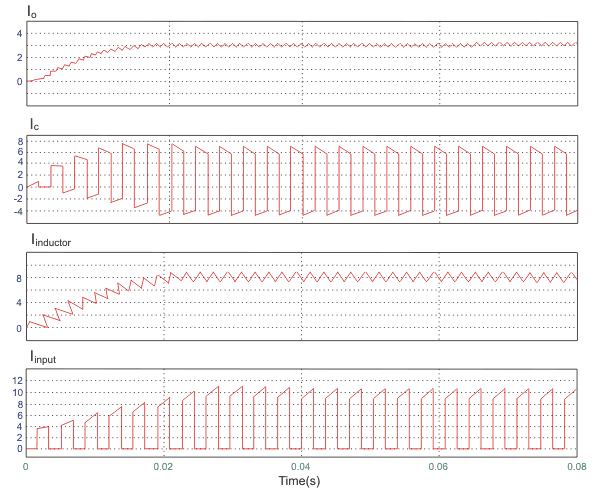
مدار یک مبدل باک بوست همراه با مقادیر عناصر آن در شکل زیر نشان داده شده است.

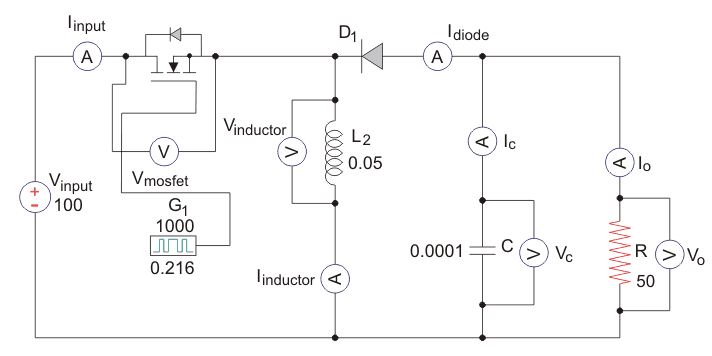
همان‌طور که می‌بینیم، اندازه اندوکتانس برابر با ۵۰ میلی‌هانری، خازن ۱۰۰ میکروفاراد و مقاومت بار ۵۰ اهم است. فرکانس سوئیچینگ نیز برابر با ۱ کیلو هرتز در نظر گرفته شده است. ولتاژ‌ ورودی ۱۰۰ ولت و چرخه وظیفه نیز برابر با ۰٫۵ در نظر گرفته شده‌اند.

شکل موج ولتاژ خروجی، ولتاژ کلید و ولتاژ سلف در شکل زیر نشان داده شده‌اند.

شکل موج‌های جریان خروجی، جریان خازن، جریان سلف و جریان ورودی نیز در شکل‌های زیر قابل مشاهده هستند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی قدرت
• آموزش الکترونیک صنعتی و مبدل ها
• مجموعه آموزش های مهندسی برق
• آموزش الکترونیک قدرت – شبیه سازی در متلب و سیمولینک
• شبیه‌سازی اینورتر در متلب — به همراه کد
• تبدیل AC به DC — راهنمای کاربردی
• یکسوساز تمام موج — به زبان ساده

^^