ماتریس هرمیتی و خصوصیات آن – به زبان ساده

در ریاضیات، ماتریس‌ها و خصوصیات آن‌ها، کاربردهای زیادی در حل مسائل بخصوص مسائل حوزه مهندسی دارند. زمانی که یک نقطه دارای بیش از یک مولفه باشد، مباحث جبر خطی و روش‌های چند متغیره به کار می‌رود. زمانی که با نقاطی یا مقادیری سر و کار دارید که دارای چند بُعد هستند، باید از ماتریس برای نمایش آن‌ها استفاده کنید. موضوع این نوشتار، ماتریس هرمیتی و خصوصیات آن است که نوع خاصی از ماتریس‌ها محسوب می‌شود که در فضای اعداد مختلط به کار می‌رود.

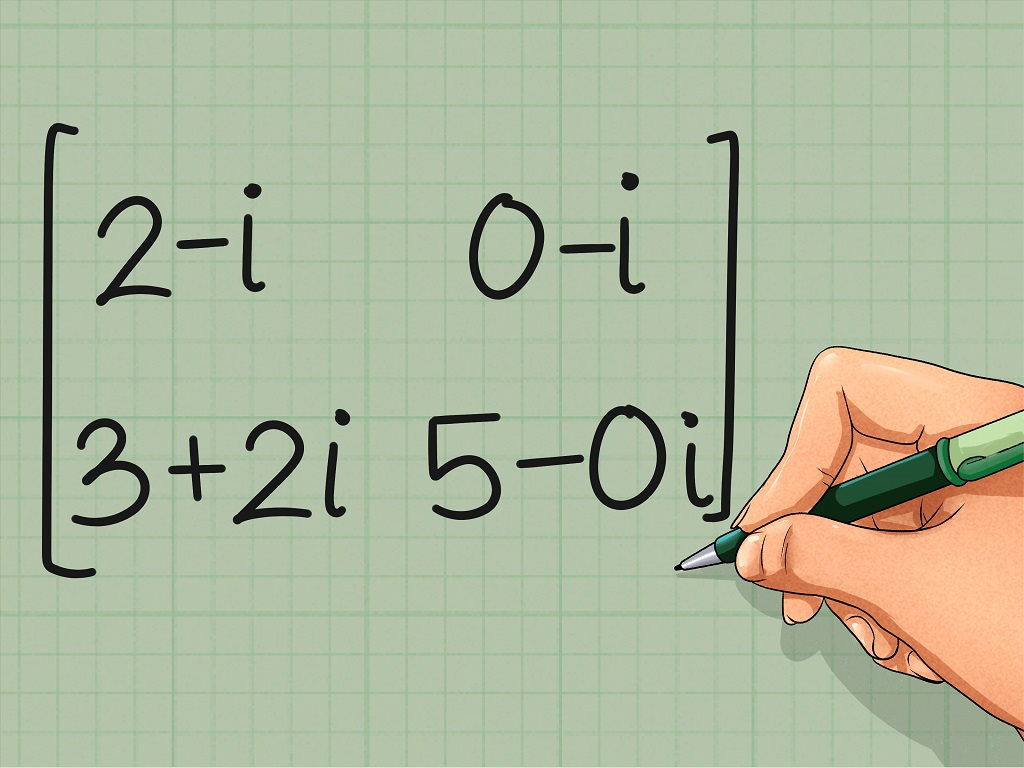
برای آشنایی بیشتر با مفاهیم اولیه در مورد ماتریس‌ها بهتر است نوشتارهای ماتریس‌ها — به زبان ساده و ترانهاده ماتریس — به زبان ساده را بخوانید. از طرفی برای درک اعداد مختلط و محاسبات روی آن‌ها مطلب اعداد مختلط – به زبان ساده را مطالعه کنید. همچنین مباحث پیچیده‌تر در حوزه محاسبات ماتریسی در مطالب ماتریس معکوس ۳×۳ — به زبان ساده و اثر ماتریس (Trace) در جبر خطی — به زبان ساده آمده است.

ماتریس هرمیتی و خصوصیات آن

در ریاضیات، ماتریس هرمیتی (Hermitan Matrix) یا «ماتریس خودالحاقی» (Self-adjoint Matrix) یک ماتریس مربعی با مقادیر مختلط است بطوری که با ترانهاده مزدوخ مختلط خود، برابر است.

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

به این ترتیب درایه سطر $$i$$ام و ستون $$j$$ام ماتریس هرمیتی برابر با مزدوج مختلط درایه سطر $$j$$ام از ستون $$i$$ام است. در نتیجه به نظر می‌رسد که ماتریس خودالحاقی، پس از ترانهاده شدن تشکیل یک ماتریس هرمیتی را می‌دهد اگر درایه‌های ماتریس اولیه با ترانهاده ماتریس خودالحاقی ‌برابر باشند.

ماتریس زیر را در نظر بگیرید.

$$\large {\displaystyle {\begin{bmatrix}2&2+i&4\\2-i&3&i\\4&-i&1\\\end{bmatrix}}}$$

همانطور که مشخص است، عناصر قطر اصلی یک ماتریس هرمیتی باید اعداد حقیقی باشند. زیرا باید با مزدوج مختلط خود برابر باشند، در نتیجه جزء موهومی در آن‌ها از بین می‌رود و تبدیل به یک عدد حقیقی می‌شوند.

از طرفی عناصر خارج از قطر اصلی باید مزدوج مختلط عنصر متناظر خود در ماتریس ترانهاده نیز باشند. به این ترتیب مشخص است که یک ماتریس هرمیتی با درایه‌های مختلط باید یک فضای برداری حقیقی-مقدار را ایجاد کند.

در ادامه به نحوه بررسی هرمیتی بودن یک ماتریس می‌پردازیم. همانطور که در زیر شاهد هستید، تعریف ماتریس هرمیتی بر حسب درایه‌های آن نوشته شده است.

$$\large {\displaystyle A{\text{ Hermitian}}\quad \iff \quad a_{ij}={\overline {a_{ji}}}}$$

رابطه ۱

اگر این رابطه را به فرم ماتریسی مشخص کنیم، می‌توانیم بنویسیم:

$$\large {\displaystyle A{\text{ Hermitian}}\quad \iff \quad A=\overline{A}^{\mathsf{T}}={\overline {A^{\mathsf {T}}}}}$$

رابطه ۲

همانطور که در تصویر زیر مشاهده می‌کنید، نحوه بررسی هرمیتی بودن ماتریس $$A$$ دیده می‌شود. ابتدا مزدوج مختلط ماتریس $$A$$، محاسبه می‌شود. سپس ترانهاده ماتریس حاصل بدست می‌آید. اگر نتیجه با خود ماتریس $$A$$ برابر باشد، ماتریس $$A$$ یک ماتریس هرمیتی است.

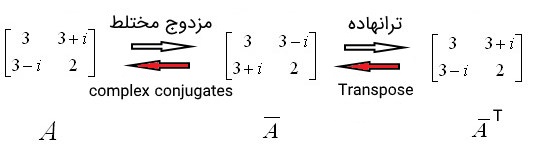
نکته: اگر $$A$$ یک ماتریس هرمیتی باشد، آنگاه $$\overline{A}^{\mathsf{T}}$$ نیز یک ماتریس هرمیتی است.

به این ترتیب می‌توانیم ماتریس هرمیتی را حالت تعمیم یافته ماتریس‌های متقارن در فضای مقادیر مختلط در نظر بگیریم. یک ماتریس متقارن در فضای اعداد حقیقی، ماتریسی است که ترانهاده آن با خود ماتریس برابر باشد. مشخص است که تعمیم این مفهوم همان ماتریس هرمیتی را در فضای مختلط بازتاب می‌دهد.

اگر ماتریس هرمیتی $$A$$ را با $$A^H$$ نشان دهیم، رابطه بالا را به صورت زیر نمایش می‌‌دهیم.

$$\large {\displaystyle A{\text{ Hermitian}}\quad \iff \quad A=A^{\mathsf {H}}}$$

رابطه ۳

تعریف و بررسی خصوصیات ماتریس‌های هرمیتی توسط چارلز هرمیت (Charles Hermite) دانشمند و ریاضی‌دان فرانسوی در سال 1855 صورت گرفت. به همین دلیل، این گونه ماتریس‌ها را به ماتریس‌های هرمیتی می‌شناسیم. این ماتریس‌ها را گاهی با نمادهای دیگری نیز نشان می‌دهند.

$$\large {\displaystyle A^{\mathsf {H}}=A^{\dagger }=A^{\ast }}$$

نکته: در فیزیک کوانتم، $$A^{\ast}$$ را به عنوان ماتریس الحاقی مختلط می‌شناسند و نه ترانهاده ماتریس الحاقی مختلط.

در ادامه مثال‌هایی ارائه می‌شود که در آن‌ها به بررسی چند ماتریس می‌پردازیم و با توجه به تعریف، هرمیتی بودن ماتریس‌ها را مشخص می‌کنیم.

مثال ۱

ماتریس $$A$$ را به شکل زیر در نظر بگیرید.

$$\large A=\begin{bmatrix}0 & -i \\i & 0 \end{bmatrix}$$

این ماتریس هرمیتی است، زیرا:

$$\large A=\begin{bmatrix}0 & -i \\i & 0 \end{bmatrix}\xrightarrow{\text{Complex Conjugates}}\begin{bmatrix}0 & i \\-i & 0 \end{bmatrix}\xrightarrow{\text{Transpose}}\begin{bmatrix}0 & -i \\i & 0 \end{bmatrix}=A$$

مثال ۲

ماتریس $$B$$ را به صورت زیر در نظر بگیرید.

$$\large B=\begin{bmatrix}1& 1&5 \\1 & 2&3\\ 5&3 &3 \end{bmatrix}$$

از آنجایی که مزدوج مختلط هر عدد حقیقی، با خودش برابر است، داریم:

$$\large \overline{B}=\begin{bmatrix}1& 1&5 \\1 & 2&3\\ 5&3 &3 \end{bmatrix}$$

حال ترانهاده ماتریس حاصل را بدست می‌آوریم.

$$\large \overline{B}^{\mathsf{T}}=\begin{bmatrix}1& 1&5 \\1 & 2&3\\ 5&3 &3 \end{bmatrix}$$

واضح است که ماتریس $$\overline{B}^{\mathsf{T}}$$ با $$B$$ برابر است. پس ماتریس $$B$$‌، هرمیتی است. البته مشخص است که ماتریس $$B$$ در فضای حقیقی، یک ماتریس متقارن است زیرا ترانهاده آن با خودش برابر است.

مثال ۳

ماتریس $$A$$ که در زیر معرفی شده است، یک ماتریس هرمیتی نیست.

$$\large A=\begin{bmatrix}0 & -i \\i & i \end{bmatrix}$$

زیرا عناصر روی قطر اصلی آن، حقیقی-مقدار نیستند.

مثال ۴

ماتریس $$A$$ که در زیر معرفی شده است، یک ماتریس هرمیتی نیست. زیرا مربعی نیست.

$$\large A=\begin{bmatrix}0 & 1&i \\i & 0&1 \end{bmatrix}$$

مثال ۵

ماتریس $$B$$ به صورت زیر تعریف شده است.

$$\large B=\begin{bmatrix}1& i&1-i \\i & 1&0\\ 1-i&0 &1 \end{bmatrix}$$

نشان می‌دهیم که $$B$$، یک ماتریس هرمیتی است. ابتدا مزدوج مختلط آن یعنی $$\overline{B}$$ را محاسبه می‌کنیم.

$$\large \overline{B}=\begin{bmatrix}1& -i&1+i \\i & 1&0\\ 1-i&0 &1 \end{bmatrix}$$

حال ترانهاده (Transpose) ماتریس $$\overline{B}$$ را بدست می‌آوریم.

$$\large \overline{B}^{\mathsf{T}}=\begin{bmatrix}1& i&1-i \\i & 1&0\\ 1-i&0 &1 \end{bmatrix}$$

از آنجایی که $$\overline{B}^{\mathsf{T}}$$ با $$B$$ برابر است، ماتریس $$B$$، هرمیتی است.

عملیات جبری روی ماتریس‌های هرمیتی

خاصیت هرمیتی برای ماتریس‌هایی که شامل مقادیر مختلط هستند، باعث ساده‌تر شدن محاسبات روی چنین ماتریس‌هایی خواهد شد. در ادامه در مورد جمع، ضرب و معکوس ماتریس‌های هرمیتی صحبت خواهیم کرد.

مجموع دو ماتریس هرمیتی

فرض کنید $$A$$ و $$B$$ دو ماتریس هرمیتی باشند، نشان می‌دهیم که مجموع این دو ماتریس نیز هرمیتی خواهد بود. به این ترتیب با توجه به تعریف جمع دو ماتریس که توسط مجموع مولفه‌های متناظر آن‌ها بدست می‌آید، خواهیم داشت:

$$\large {\displaystyle (A+B)_{ij}=A_{ij}+B_{ij}}=$$

$$\large {\overline {A}}_{ji}+{\overline {B}}_{ji}={\overline {(A+B)}}_{ji}$$

تساوی مربوط به خط دوم رابطه بالا، با توجه به هرمیتی بودن ماتریس $$A$$ و $$B$$ نوشته شده است. به این معنی که عناصر پایین قطر اصلی، مزدوج مقادیر متناظرشان در بالای قطر اصلی هستند. این موضوع در رابطه ۱ نشان داده شده است.

ضرب دو ماتریس هرمیتی

شرط لازم و کافی برای آنکه ضرب دو ماتریس هرمیتی، یک ماتریس هرمیتی باشد، آن است که $$AB=BA$$ باشد. این امر به واسطه روابط زیر حاصل می‌شود.

$$\large {\displaystyle (AB)^{\mathsf {H}}={\overline {(AB)^{\mathsf {T}}}}={\overline {B^{\mathsf {T}}A^{\mathsf {T}}}}={\overline {B^{\mathsf {T}}}}{\overline {A^{\mathsf {T}}}}=B^{\mathsf {H}}A^{\mathsf {H}}=BA}$$

با توجه به رابطه ۲، شرط آن که $$BA$$ ماتریس هرمیتی باشد آن است که $$BA=AB$$ باشد و برعکس.

به این ترتیب اگر ضرب دو ماتریس هرمیتی، خاصیت جابجایی داشته باشد، آنگاه حاصل‌ضرب آن‌ها نیز هرمیتی خواهد بود.

معکوس یک ماتریس هرمیتی

حال به بررسی ماتریس معکوس $$A$$ و شرایط هرمیتی بودن آن‌ها خواهیم پرداخت. فرض کنید $$A^{-1}$$ معکوس ماتریس $$A$$ باشد. همچنین می‌دانیم که ماتریس $$A$$، هرمیتی است. از طرفی چون ماتریس یکه $$I$$، قطری بوده و عناصر خارج از قطر همگی صفر هستند، یک ماتریس هرمیتی محسوب می‌شود. پس داریم:

$$\large {\displaystyle I=I^{H}=(A^{-1}A)^{H}=A^{H}(A^{-1})^{H}=A(A^{-1})^{H}}$$

به این ترتیب اثبات می‌شود که معکوس یک ماتریس هرمیتی نیز هرمیتی است. به بیان دیگر مطابق با رابطه ۲ داریم:

$$\large {\displaystyle A^{-1}=(A^{-1})^{H}}$$

خصوصیات ماتریس هرمیتی

مشخصه و ویژگی‌ها ماتریس هرمیتی در ادامه مورد بررسی قرار می‌گیرند.

• مطابق با تعریف ارائه شده برای ماتریس هرمیتی، مشخص است که ماتریس مربع $$A$$، یک ماتریس هرمیتی است اگر و فقط اگر با ترانهاده همسازه خود برابر باشد. به بیان ریاضی اگر $$v$$ و $$w$$ دو بردار و $$\langle\cdot,\cdot \rangle$$ عملگر ضرب داخلی باشند، خواهیم داشت:

  $$\large {\displaystyle \langle w,Av\rangle =\langle Aw,v\rangle }$$
  رابطه ۴

• اگر $$A$$ یک ماتریس هرمیتی باشد، آنگاه رابطه زیر برقرار است و برعکس.

  $$\large {\displaystyle \langle v,Av\rangle \in \mathbb {R} ,\quad v\in V}$$

• درایه‌های قطر اصلی یک ماتریس هرمیتی حتما حقیقی هستند.
• ماتریس‌های هرمیتی، یک ماتریس نرمال هستند به این معنی که حاصل ضرب‌ آن‌ها در ترانهاده‌شان، خاصیت جابجایی دارد.

  $$\large AA^{\mathsf{T}}=A^{\mathsf{T}}A$$

• مقادیر ویژه ماتریس هرمیتی A، مقادیر حقیقی هستند.
• بردارهای ویژه ماتریس هرمیتی A، بر یکدیگر متعامدند.

برای روشن شدن این خصوصیات، در ادامه توضیحاتی ارائه می‌شود.

نرمال بودن ماتریس هرمیتی

همانطور که گفته شد هر ماتریس هرمیتی، نرمال نیز هست. این ویژگی را به صورت زیر اثبات می‌کنیم.

فرض کنید $$A$$ یک ماتریس هرمیتی است. در نتیجه خواهیم داشت:

$$\large \overline{A}^{\mathsf{T}}= A$$

دو طرف این تساوی را در ماتریس $$A$$ ضرب می‌کنیم. (توجه دارید که ماتریس $$A$$‌ مربعی است).

$$\large A\overline{A}^{\mathsf{T}}= AA$$

از آنجایی که ماتریس $$A$$ هرمیتی است، طرف راست تساوی بالا را تغییر می‌دهیم. در نتیجه رابطه به صورت زیر در می‌آید.

$$\large A\overline{A}^{\mathsf{T}}= AA=\overline{A}^{\mathsf{T}}A$$

پس خواهیم داشت:

$$\large A\overline{A}^{\mathsf{T}}=\overline{A}^{\mathsf{T}}A$$

برای مثال ماتریس زیر یک ماتریس نرمال است، زیرا یک ماتریس هرمیتی است.

$$\large A= \begin{bmatrix}2 & 1-2i \\1+2i & 3 \end{bmatrix}$$

مقادیر ویژه ماتریس هرمیتی

برای نشان دادن این موضوع، از تعریف مقدار ویژه ماتریس استفاده می‌کنیم. اگر $$\lambda$$‌، مقدار ویژه ماتریس $$A$$ باشد، آنگاه داریم:

$$\large Av=\lambda v$$

رابطه ۵

که در آن $$v$$ بردار ویژه ماتریس $$A$$ خواهد بود. حال فرض کنید که $$A$$ یک ماتریس هرمیتی است. نشان می‌دهیم که مقدارهای $$\lambda$$ که بیان‌گر مقدارهای ویژه ماتریس $$A$$ هستند، همگی حقیقی خواهند بود. برای این کار ابتدا دو طرف رابطه بالا را در  $$\overline{v}^{\mathsf{T}}$$ ضرب می‌کنیم.

$$\large \overline{v}^{\mathsf{T}}(Av)=\overline{v}^{\mathsf{T}}(\lambda v)=\lambda \overline{v}^{\mathsf{T}}v=\lambda||v||$$

رابطه 6

به این ترتیب براساس رابطه ۶، می‌توان نوشت:

$$\large \overline{v}^{\mathsf{T}}(Av)=(Av)^{\mathsf{T}}\overline{v}=(v^{\mathsf{T}}A)\overline{v}$$

رابطه ۷

رابطه ۷ از آنجا ناشی می‌شود که $$Av$$ و $$v$$ هر دو بردار بوده و ضرب ترانهاده بردار ستونی در همان بردار، یک عدد خواهد شد. حال مزدوج مقدار رابطه ۷ را محاسبه می‌کنیم. از آنجایی که اگر دو عدد برابر باشند، مزدوج آن‌ها هم برابر خواهند بود، خواهیم داشت:

$$\large \overline{\overline{v}^{\mathsf{T}}(Av)}=v^{\mathsf{T}}\overline{(Av)}=\overline{\lambda}||v||$$

رابطه ۸

با توجه به رابطه ۶، ۷ و ۸ داریم:

$$\large\overline{\lambda}||v||= \lambda||v||$$

پس دو مقدار $$\lambda$$ و $$\overline{\lambda}$$ برابرند. این امر برای دو عدد مختلط فقط زمانی رخ می‌دهد که هر دو عدد، جزء موهومی نداشته باشند. در نتیجه مقادیر ویژه ماتریس هرمیتی، اعداد حقیقی هستند.

متعامد بودن بردارهای ویژه ماتریس هرمیتی

یکی دیگر از خصوصیات جالب برای ماتریس‌های هرمیتی، متعامد بودن بردارهای ویژه آن‌ها است. به این ترتیب فضایی که از بردارهای ویژه ماتریس‌های هرمیتی ایجاد می‌شود، یک فضای متعامد است. در این قسمت به بررسی این موضوع می‌پردازیم.

فیلم آموزش ریاضی فیزیک ۱ + مفاهیم کلیدی در فرادرس

کلیک کنید

فرض کنید $$\lambda_1$$ و $$\lambda_2$$ دو مقدار ویژه متمایز از ماتریس هرمیتی $$A$$ باشند و همچنین در نظر بگیرید که بردارهای ویژه متناظر با این مقادیر نیز با $$v$$ و $$v'$$ مشخص شده‌اند و از یکدیگر متمایز باشند.

در قسمت قبل نشان دادیم که مقادیر ویژه ماتریس هرمیتی، حقیقی هستند. پس باید داشته باشیم:

$$\large\lambda_1\langle v,v'\rangle=\langle \lambda_1v,v'\rangle=\langle Av,v'\rangle\\ \large \overset{\text{A Hermitian}} =\langle v,Av'\rangle =\langle v,\lambda_2v'\rangle=\lambda_2\langle v,v'\rangle$$

توجه داشته باشید که تساوی دوم و سوم به علت خاصیت هرمیتی ماتریس $$A$$ نوشته شده است.

از آنجایی که مقادیر ویژه $$\lambda_1$$ و $$\lambda_2$$‌ و بردارهای ویژه متناظر آن‌ها متمایز هستند، تساوی بالا فقط زمانی برقرار است که ضرب داخلی $$v$$ و $$v'$$ صفر باشد. این موضوع بیانگر متعامد بودن این دو بردار است. در نتیجه فضای تشکیل شده توسط بردارهای ویژه‌ متمایز یک ماتریس هرمیتی، تشکیل یک فضای متعامد می‌دهد.

مثال ۶

فرض کنید که ماتریس $$A$$ به صورت زیر باشد.

$$\large \begin{bmatrix}1 & 1-i \\1+i & 2 \end{bmatrix}$$

با توجه به شیوه محاسبه بردار و مقادیر ویژه این ماتریس داریم:

$$\large A-\lambda I=\begin{bmatrix}1-\lambda & 1-i \\1+i & 2-\lambda \end{bmatrix}$$

حال با مساوی قرار دادن دترمینان ماتریس حاصل، مقادیر ویژه را محاسبه می‌کنیم.

$$\large \det( A-\lambda I)=(1-\lambda)(2-\lambda)-(1-i)(1+i)=\lambda^2-3\lambda=0$$

پس $$\lambda_1=0$$ و $$\lambda_2=3$$. حال بردارهای ویژه را با توجه به تعریف بردارهای ویژه ماتریس $$A$$، مورد محاسبه قرار می‌دهیم.

ابتدا بردار ویژه متناظر با مقدار ویژه $$\lambda_1=0$$ را بدست می‌آوریم.

$$\large Av=\lambda_1v\;\xrightarrow{\lambda_1=0} \begin{bmatrix}1 & 1-i \\1+i & 2\end{bmatrix}(v_1,v_2)^{\mathsf{T}}=0\rightarrow \begin{bmatrix}v_1+v_2(1-i) \\v_1(1+i)+2v_2\end{bmatrix}$$

از آنجایی که بردار باید صفر باشد، مولفه اول و دوم آن، صفر خواهد بود. در نتیجه می‌توان با صفر قرار دادن هر یک از مولفه‌ها، بردار ویژه متناظر با $$\lambda_1=0$$ را بدست آورد.

$$\large v_1+v_2(1-i)= 0 \rightarrow v_1=-(1-i)v_2$$

نکته: اگر مولفه دوم را هم برابر با صفر قرار دهیم، به همین نتیجه برای بردار ویژه خواهیم رسید. واضح است که به علت سادگی محاسبات، از مولفه اول استفاده کرده‌ایم.

$$\large v_1(1+i)+2v_2=0 \rightarrow v_1=-\dfrac{2v_2}{(1+i)}=\\ \large v_1=-\dfrac{2v_2}{(1+i)}\times \dfrac{(1-i)}{(1-i) }=-\dfrac{2(1-i)v_2}{(1+i)(1-i)}=\\ \large -\dfrac{2(1-i)v_2}{2}=-(1-i)v_2$$

در ادامه بردار ویژه متناظر با مقدار $$\lambda_2=3$$ را محاسبه می‌کنیم.

$$\large Av=\lambda_2v'\;\xrightarrow{\lambda_2=3}\; \begin{bmatrix}1 & 1-i \\1+i & 2\end{bmatrix}(v_1,v_2)^{\mathsf{T}}=3(v_1,v_2)^{\mathsf{T}}\\ \large\rightarrow \begin{bmatrix}v_1+v_2(1-i) \\v_1(1+i)+2v_2\end{bmatrix}=\begin{bmatrix}3v_1\\3v_2\end{bmatrix}$$

با مساوی قرار دادن هر یک از مولفه‌ها خواهیم داشت:

$$\large v_1+v_2(1-i)=3v_1\\ \large v_1(1+i)+2v_2=3v_2$$

از تساوی اول، به رابطه $$v_1=\frac{v_2}{2}(1-i)$$‌ خواهیم رسید. البته اگر از رابطه دوم نیز استفاده می‌کردیم، باز هم همین بردار بدست می‌آمد.

حال، ضرب داخلی بردار ویژه اول (حاصل از مقدار ویژه $$\lambda_1=0$$) و بردار ویژه دوم (حاصل از مقدار ویژه $$\lambda_2=3$$) را محاسبه کرده و نشان می‌دهیم که حاصل صفر خواهد بود.

$$\large \langle v,v'\rangle =-(1-i)v_2\times \dfrac{v_2}{2}\overline{(1-i)}+v_2^2=\\ \large-(1-i)v_2\times \dfrac{v_2}{2}(1+i)+v_2^2=\\ \large-v_2^2+v_2^2=0$$

نکته: از آنجایی که ضرب داخلی دو بردار با مولفه‌های مختلط به صورت مجموع حاصل ضرب مولفه‌های بردار اول با مزدوج مولفه‌های بردار دوم حاصل می‌شود، رابطه مربوط به سطر اول و دوم را نوشته‌ایم.

خلاصه و جمع‌بندی

در این نوشتار با ماتریس هرمیتی و خواص آن آشنا شدیم. همچنین نحوه محاسبات جبری روی چنین ماتریس‌هایی نیز مورد بحث قرار دادیم. مشخص است که ماتریس هرمیتی تعمیم یافته ماتریس متقارن در فضای مختلط است. به این ترتیب در چنین فضاهایی محاسبات ماتریس هرمیتی اهمیت پیدا کرده و مورد استفاده قرار می‌گیرد.

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ریاضیات مهندسی
• مجموعه آموزش‌های آمار و احتمالات
• آموزش جبر خطی با متلب
• بردار و اسکالر — به زبان ساده
• ماتریس متعامد — از صفر تا صد
• بردار ویژه و مقدار ویژه — از صفر تا صد

^^