ماتریس مجاورت چیست؟ – به زبان ساده + انواع گراف و حل مثال
ماتریس مجاورت یا Adjacency Matrix در ریاضیات عمومی نوعی ماتریس مربعی است و با نمایش اینکه کدام راسها یا گرهها به هم متصل هستند، به توصیف یک گراف میپردازد. اگر دو راس گرافی توسط یک یال به هم متصل شده باشند، موقعیت متناظر در این ماتریس عدد است، در غیر این صورت عدد را داریم. در این مطلب از مجله فرادرس توضیح میدهیم ماتریس مجاورت چیست، چه فرمولی دارد و چگونه میتوان از آن در زمینه نمایش انواع گراف استفاده کرد.
- با تعریف و کاربرد ماتریس مجاورت آشنا میشوید.
- یاد میگیرید چگونه انواع گراف را توسط ماتریس مجاورت توصیف کنید.
- کاربردهای این نوع ماتریس در تشخیص ویژگیهای گراف مانند درجه هر راس را خواهید شناخت.
- انواع ماتریس مجاورت را خواهید دانست.
- محاسبات مربوط به توانهای ماتریس مجاورت را میآموزید.
- با جزئیات مربوط به این ماتریسها در پایتون و سی پلاس پلاس آشنا میشوید.


ماتریس مجاورت چیست و چه فرمولی دارد؟
ماتریس مجاورت یک ماتریس مربعی است که اتصالات در یک گراف متناهی را نشان میدهد. در این ماتریس، هر سطر و هر ستون مربوط به یک راس یا گره است. همچنین درایههای این ماتریس که معمولا یا هستند، وجود یا عدموجود یال بین راسها را مشخص میکنند. به این ترتیب برای گرافی به نام با راس که به شکل نامگذاری شدهاند، ماتریس مجاورت ماتریسی است که هر درایه آن به شکل زیر تعریف میشود:
در رابطه بالا اگر یالی از تا وجود داشته باشد، است و در غیر این صورت .
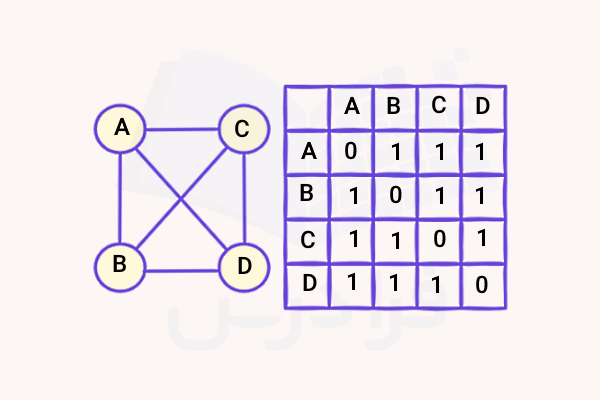
برای نمونه، تصویر بالا نوعی ماتریس مجاورت را نشان میدهد که برای توصیف یک گراف کامل بکار میرود. مفهوم ماتریس مجاورت کاربردهای گستردهای در نظریه گراف، ریاضیات گسسته، ساختارهای داده و بسیاری از مسائل شبکهای دارد.
همچنین در سطوح پایه بکارگیری این ماتریس به دانشآموزان کمک میکند تا روابط بین اشیا را بهتر درک کنند. به علاوه ماتریس مجاورت ارتباط نزدیکی با موضوعاتی مانند ماتریس متقارن و ماتریس رخداد یا ماتریس وقوع دارد. تسلط بر ماتریس مجاورت، به یادگیری الگوریتمها و ساختارهای دادهای پیچیدهتر در آینده کمک میکند.
نمایش ماتریس مجاورت
اگر بخواهیم ماتریس مجاورت متناظر با یک گراف را رسم کنیم، کافی است به ویژگیهای آن گراف از جمله تعداد و نام راسها، تعداد و نام یالها و همچنین جهتدار یا بیجهت بودن یالهای آن توجه کنیم. برای مثال، فرض کنید برای گرافی رئوسی با نامهای و یالهایی به شکل و و و را داریم که همگی بدون جهت هستند.
در این صورت ماتریس مجاورت متناظر با آن به شکل زیر نمایش داده میشود:
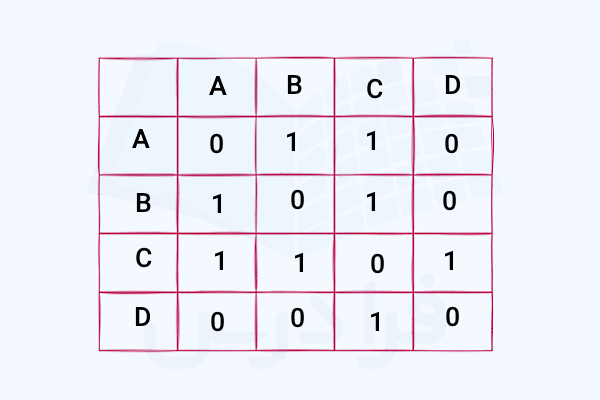
هر درایه با مقدار در این ماتریس نشان دهنده این است که دو راس توسط یک یال به هم متصل شدهاند. از آنجایی که در توصیف این گراف این نکته ذکر شده است که یالها جهت ندارند، پس لازم است برای مثال در مورد یال درایه متناظر با جهت معکوس یعنی را نیز برابر با در نظر بگیریم. در حالی که اگر این گراف جهتدار بود، یکی از این دو درایه صفر میشد. در بخشهای بعد با ویژگی جهتدار بودن، انواع گراف و ماتریسهای مجاورت متناظر با آنها بیشتر آشنا میشوید.
یادگیری ماتریس و هندسه تحلیلی با فرادرس
پیش از توضیح انواع ماتریس مجاورت، ابتدا قصد داریم چند فیلم آموزشی در زمینه مباحث مطرح شده در کتاب هندسه تحلیلی متوسطه دوم را معرفی کنیم. مشاهده این دورهها به شما کمک میکند تا از طریق مشاهده تصاویر، یادگیری عمیقتری داشته باشید. ضمن اینکه اغلب این آموزشها همراه با حل مثالها و تمرینهای متنوعی است که به درک بهتر شما از موضوعات مختلف از جمله ماتریسها کمک خواهد کرد:
- فیلم آموزش هندسه پایه دوازدهم رشته ریاضی و فیزیک فرادرس
- فیلم آموزش ریاضی پایه دوازدهم علوم تجربی فرادرس
انواع ماتریس مجاورت
از ماتریسهای مجاورت برای توصیف یا نمایش گرافهای جهتدار و بیجهت استفاده میشود. در مورد گرافهای بیجهت این ماتریس متقارن است، چون هر یال در دو جهت عمل میکند. اما در مورد گرافهای جهتدار ماتریس ممکن است متقارن نباشد:
- گرافهای بیجهت: در یک گراف بیجهت اگر راس به راس متصل باشد، درایه و هر دو مساوی خواهند شد. در نتیجه ماتریس متقارن است.
- گرافهای جهتدار: در یک گراف جهتدار درایه در صورتی برابر با است که یک یال از راس به راس وجود داشته باشد. در این حالت ممکن است ماتریس نامتقارن باشد.
- گرافهای وزندار: برای گرافهایی که یالها دارای وزن (مانند مسافت) هستند، درایه میتواند به جای مقدار وزن یال را نشان دهد.
عملکرد و ویژگی های ماتریس مجاورت
بهطور خلاصه عملکرد ماتریس مجاورت توسط دو مورد زیر تعریف میشود:
- راسها به عنوان سطر و ستون: برای گرافی با راس، ماتریس مجاورت یک ماتریس خواهد شد.
- درایهها نشاندهنده اتصالات: درایه در موقعیت نشان میدهد که یک یال بین راس و راس وجود دارد، در حالی که درایه نشاندهنده عدموجود یالی مستقیم بین آن دو راس است.
همچنین ویژگیهای زیر را میتوانیم از جمله مهمترین ویژگیهای یک ماتریس مجاورت در نظر بگیریم:
- اگر گراف بیجهت باشد، ماتریس مجاورت متقارن است، یعنی داریم: .
- درایههای روی قطر اصلی حلقههای خودی یا Self Loops را نشان میدهند، به این معنا که اگر در آن راس حلقه وجود داشته باشد، درایه برابر با میشود و در غیر این صورت آن درایه است.
- جمع درایههای یک سطر یا ستون درجه یا Degree راس را نشان میدهد.
- ضرب ماتریس در خودش (به توان رساندن) اطلاعاتی درباره مسیرهایی با طول بیشتر را به ما نشان میدهد.
- در مورد گرافهای وزندار، مقدار با وزن یال جایگزین میشود.
نظریه گراف و ارتباط آن با ماتریس مجاورت
در این بخش مروری داریم بر نظریه گراف تا بهتر متوجه شوید مبنای ارتباط گرافها و ماتریس مجاورت چیست. یک گراف عموما توسط نموداری مانند شکل سمت چپ در تصویر زیر نمایش داده میشود. همچنین این گراف را میتوان در قالب ماتریسی به نام ماتریس مجاورت (شکل سمت راست) نمایش داد:
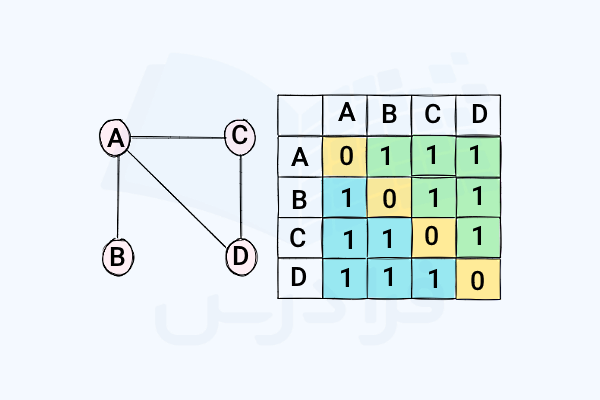
ماتریس مجاورت اطلاعات نمودار گراف را به شکل دیگری اما بهطور دقیق بیان میکند. اصولا رسم نمودار گراف برای تجسم سادهتر است، اما شکل ماتریسی گراف نیز مفید است، چون امکان تحلیل و انجام محاسبات ریاضیاتی را برای ما فراهم میکند. همچنین با توجه به اینکه ماتریس در واقع جدولی از اعداد است، پس میتوانیم آن را بهراحتی توسط یک برنامه کامپیوتری پردازش کنیم. در ادامه با انواع گراف و ماتریس مجاورت هر کدام بیشتر آشنا خواهیم شد.
گراف ساده
گرافی که در ابتدای این بخش رسم شد، یک گراف ساده یا Simple Graph با چهار راس است که بین آنها یالهای سادهای وجود دارد. در ماتریس مجاورت این گراف ساده، مقدار را داریم که نشان میدهد دو راس به هم متصل هستند و مقدار را برای حالتی داریم که راسها به هم متصل نیستند. برای مثال، درایه متناظر با سطر و ستون برابر با است، چون بین این دو راس یک یال وجود دارد. اما درایه متناظر با سطر و ستون برابر با است، چون بین این دو راس هیچ یالی وجود ندارد.
نکته جالب توجه در نمایش ماتریسی این گراف این است که تمام درایههای روی قطر اصلی (با زمینه رنگ زرد) صفر هستند، چون هیچ راسی به خودش متصل نیست. برای نمونه، درایه متناظر با سطر و ستون صفر است، چرا که راس به خودش متصل نیست. همچنین توجه کنید که این ماتریس نسبت به قطر اصلی متقارن است، به این معنا که ناحیه آبی رنگ انعکاسی از ناحیه سبز رنگ است. تقارن به این دلیل است که در یک گراف ساده، هر یال در هر دو جهت عمل میکند. برای مثال، اگر به متصل باشد، این به معنی آن است که هم به توسط همان یال متصل است.
گراف ساده با حلقه
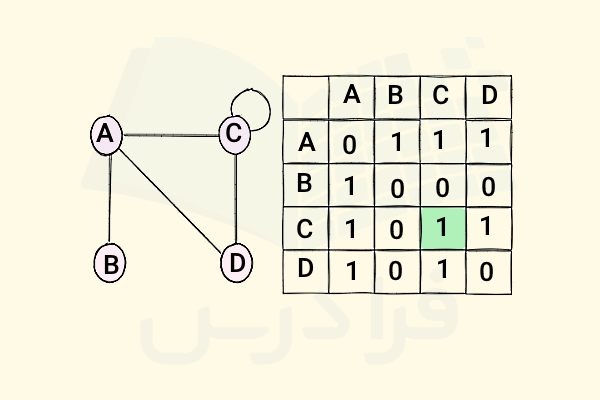
این نوع گراف همان گراف ساده است، با این تفاوت که حداقل روی یک راس آن یک حلقه وجود دارد. برای مثال مطابق تصویر زیر، حلقهای روی راس داریم، به این معنا که راس به خودش متصل است. به این ترتیب درایه متناظر با سطر و ستون برابر است با مقدار که نشان میدهد در گراف متناظر با این ماتریس مجاورت یک حلقه وجود دارد:
گراف جهت دار
تصویر زیر نمودار یک گراف جهتدار را نمایش میدهد. در گراف جهتدار، هر یال فقط در یک جهت عمل میکند. برای مثال در گراف زیر یک یال از به وجود دارد، اما یالی از به وجود ندارد. دقت کنید یک گراف جهتدار لزوما نسبت به قطر اصلی متقارن نیست، چون وجود یک یال در یک جهت لزوما به معنای وجود یال در جهت مخالف آن نیست.
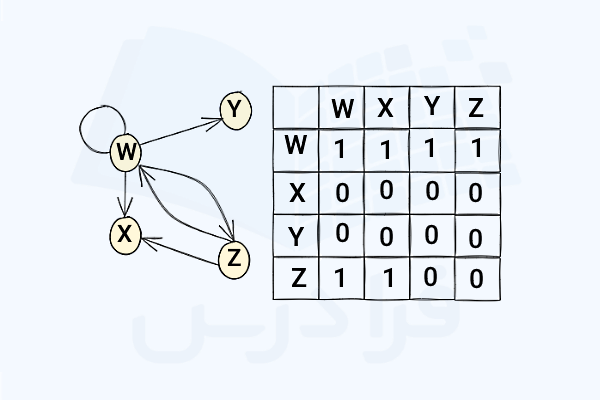
اگر اتصال دو راس دو طرفه باشد، این موضوع با دو یال نشان داده میشود. برای مثال یال بین دو راس و دو طرفه است. در این حالت در هر دو جایگاه ماتریس مقدار قرار میگیرد. همچنین یک حلقه نیز نشان داده شده است که طبق آن راس به خودش متصل است. این موضوع نیز با عدد مشخص میشود. باید دقت داشته باشید که حتی در یک ماتریس جهتدار، حلقه جهت ندارد. در حقیقت حلقه را به متصل میکند، بنابراین هیچ جهتی برای آن در نظر گرفته نمیشود.
گراف چندگانه
در یک گراف چندگانه یا Multigraph میتوانیم بین دو راس، بیش از یک یال داشته باشیم. این گراف میتواند جهتدار یا بدون جهت باشد. در تصویر زیر نمونهای از یک گراف چندگانه بدون جهت را ملاحظه میکنید. در این حالت، بین راسهای و دو یال وجود دارد. همچنین ماتریس مجاورت در مورد این گراف کمی با ماتریس مجاورت گراف ساده متفاوت است، زیرا در اینجا هر درایه تعداد یالها را نشان میدهد. چون تعداد یالهای بین دو راس و برابر است با ، پس درایه متناظر نیز است.
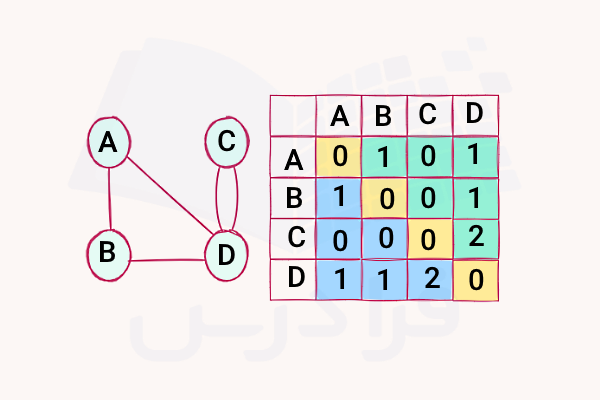
همچنین اگر بین دو راس هیچ یالی وجود نداشته باشد، مقدار آن است (مشابه گراف ساده). به عنوان مثال، درایه متناظر با یالی که بین دو راس و وجود دارد، برابر با است زیرا و به هم متصل نیستند. نکته دیگر این است که ماتریس بالا متقارن است، چون یک گراف بدون جهت را نمایش میدهد. اگر گراف جهتدار بود، ماتریس میتوانست نامتقارن باشد. قطر اصلی این ماتریس نیز کاملا شامل مقادیر است، مگر اینکه گراف دارای حلقه باشد. این ویژگی نیز مشابه گراف ساده است.
گراف وزن دار
در یک گراف وزندار یا Weighted Graph هر یال دارای مقداری است که به آن وزن گفته میشود. گرافهای وزندار نیز میتوانند جهتدار یا بدون جهت باشند، اما در اینجا فقط حالت بدون جهت را بررسی میکنیم. ماتریس مجاورت در گراف وزندار، وزن یالها را نشان میدهد. برای مثال، درایههای متناظر برای دو راس و و همچنین رئوس و هر دو برابر با است، زیرا یال بین و وزنی برابر با دارد.
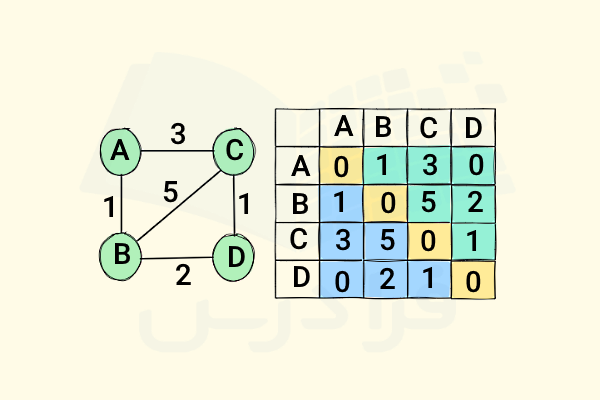
برای حالتی که هیچ یالی وجود ندارد، باید از یک مقدار ویژه استفاده کنیم. در این مثال، از مقدار برای نشان دادن عدم وجود یال استفاده میکنیم، با این فرض که اگر یالی وجود داشته باشد، وزن آن نمیتواند صفر باشد. برای مثال، اگر گرافی نمایانگر یک شبکه جادهای باشد و وزنها نشاندهنده فاصلهها باشند، منطقی است که بگوییم هیچ جادهای طول صفر ندارد، بنابراین میتوانیم از برای نشان دادن عدم وجود جاده استفاده کنیم.
البته در برخی سیستمها ممکن است داشتن یالی با وزن صفر معتبر باشد. در این صورت لازم است از مقدار دیگری برای نشان دادن عدم وجود یال استفاده شود (برای مثال اگر وزنهای منفی معتبر نباشند). گرافهای چندگانه وزندار را نمیتوان بهراحتی با ماتریس مجاورت نمایش داد، زیرا یک جفت راس میتواند چند مقدار (چند یال با وزنهای متفاوت) داشته باشد.
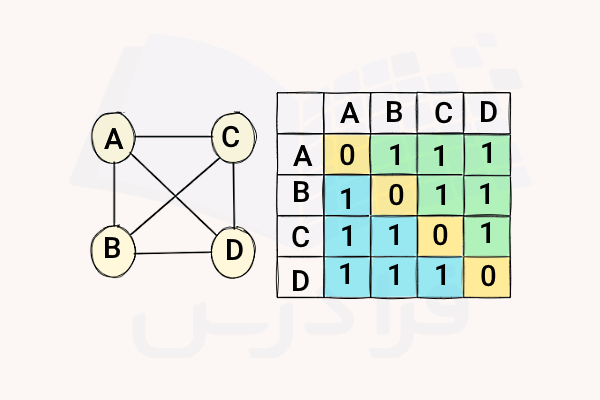
گراف کامل
گراف کامل یا Complete Graph گرافی است که در آن هر راس به تمام راسهای دیگر متصل است. در این نوع گراف، به جز درایههای روی قطر اصلی سایر درایهها مخالف صفر هستند. این به این معنا است که بین هر جفت راس غیرمشابه یک یال وجود دارد. تصویر زیر این نوع گراف و ماتریس مجاورت آن را بهخوبی نشان میدهد:
گراف ایزومورف و ماتریس جابجایی
به دو گراف در تصویر زیر ایزومورف یا یکریخت گفته میشود، چنانچه گرافهایی معادل باشند که تنها تفاوت آنها در نامگذاری راسها و / یا نحوه نمایش آنهاست. در حقیقت اگر به ماتریسهای مجاورت دو گراف ایزومورف نگاه کنیم، آنها یکسان هستند، به جز اینکه ممکن است ترتیب سطرها و ستونهای آنها متفاوت باشد.
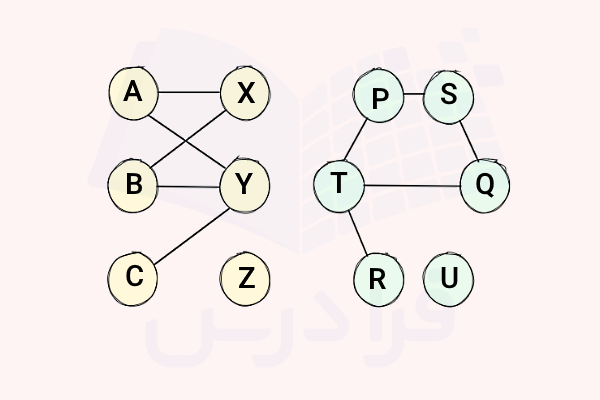
همچنین در همین زمینه مفهومی به نام ماتریس جایگشت یا Permutation Matrix را داریم که یک ماتریس خاص است و وظیفه آن تغییر ترتیب سطرها و ستونها است. برای هر دو گراف ایزومورف، میتوان با اعمال یک ماتریس جایگشت مناسب به یکی از آنها دو ماتریس را کاملا یکسان کرد. در انتهای این بخش پیشنهاد میکنیم جهت آشنایی با انواع گرافها مطلب زیر از مجله فرادرس را مطالعه نمایید:
بررسی ویژگی های گراف به کمک ماتریس مجاورت
در این بخش توضیح میدهیم یکی از کاربردهای مهم ماتریس مجاورت چیست. به کمک ماتریس مجاورت میتوانیم ویژگیهای مختلف یک راس را تعیین کنیم. توضیحات این بخش مربوط به گرافهای ساده است، اما میتوان این روشها را برای گرافهای جهتدار، وزندار یا گرافهای چندگانه نیز بکار برد.
به ماتریس مجاورت گراف ساده حلقهدار در تصویر زیر توجه کنید. همانطور که قبلا اشاره کردیم، قطر اصلی ماتریس مجاورت نشان میدهد که آیا گراف ما دارای حلقه است یا خیر. در این مثال، درایههای روی قطر اصلی صفر نیستند، بنابراین راس دارای یک حلقه است. همچنین میتوانیم بهراحتی درجه یک راس، یعنی تعداد یالهایی که به آن متصل هستند را با توجه به ماتریس مجاورت بررسی کنیم. برای رسیدن به این هدف، کافی است تعداد یکها را در سطر مربوط به آن راس جمع کنیم (در تصویر بالا میتوانیم از ستون نیز استفاده کنیم، چون ماتریس داده شده متقارن است).
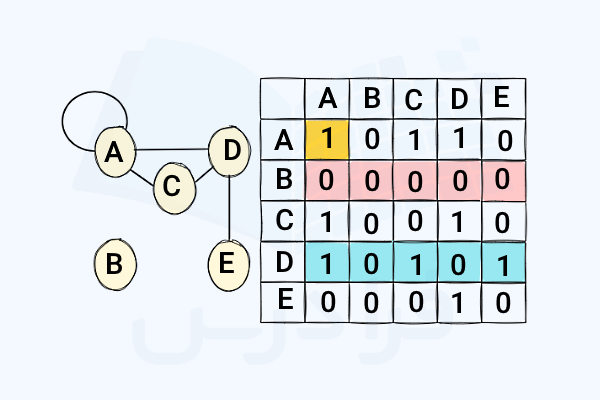
برای مثال راس درجه دارد، زیرا سه عدد را در سطر داریم که در شکل با رنگ آبی مشخص شدهاند. همچنین درجه راس نیز است، چون هیچ عدد برابر با یکی در سطر وجود ندارد (در شکل با رنگ صورتی مشخص شده است). این جمله به این معنا است که راس جدا افتاده است. با نگاه کردن به شکل گراف نیز این موضوع را مشاهده خواهید کرد.
از طرفی راس را داریم که یک حالت خاص است، چون حلقه دارد. حلقه به عنوان دو اتصال شمرده میشود، چون دو بار به همان راس وصل میشود. بنابراین هنگام جمع زدن تعداد یکهای موجود در سطر، اگر درایه قطر اصلی مقداری مخالف صفر داشته باشد، باید آن را بهجای عدد در نظر بگیریم. پس در این مثال، راس درجهای برابر با مقدار دارد. پس تا حدی یاد گرفتیم که چگونه میتوان از ماتریس مجاورت برای تعیین ویژگیهای یک گراف استفاده کرد. در همین راستا، اینکه آیا گراف ما درخت است یا خیر، متصل است یا خیر، دو بخشی است یا خیر و ... نیز با استفاده از الگوریتمهای ساده و قابلاجرا روی ماتریس مجاورت مشخص میشوند.
توان های ماتریس مجاورت
در این بخش توضیح میدهیم منظور از توانهای ماتریس مجاورت چیست. میدانیم ماتریس مجاورت یک گراف ساده را میتوان به این صورت تفسیر کرد که مقدار درایه متناظر برای هر دو راس نوعی برابر با یک است، اگر بین آن دو راس یک یال وجود داشته باشد. بر این اساس، مجذور ماتریس مجاورت یعنی ماتریسی که در خودش ضرب شده است، ویژگی جالب دیگری ارائه میدهد. اگر مقدار عددی درایه متناظر برای دو راس نوعی و را با نشان دهیم، در این صورت برابر است با تعداد مسیرهای ممکن بین راس و که طول آنها دقیقا برابر با است.
به همین شکل، توان سوم ماتریس مجاورت نیز الگوی مشابهی دارد. پس مقدار برابر است با تعداد مسیرهای ممکن بین راس و راس که طول آنها دقیقا برابر با است. برای توانهای بالاتر نیز روند به همین صورت است. البته توجه داشته باشید که این ویژگی به عبورها یا Walks مربوط میشود، نه به مسیرها یا Paths. گذر یا عبور مسیری بین دو راس است که اجازه دارد از یک راس بیشتر از یک بار عبور کند. برای مثال اگر بین دو راس و یک یال وجود داشته باشد، یک گذر با طول از به وجود دارد. اما ممکن است در کنار آن، یک گذر با طول هم وجود دارشته باشد که از به میرود، سپس به برمیگردد و دوباره به میرود.
حل مثال از ماتریس مجاورت
در بخشهای قبل آموختیم مارتیس مجاورت چیست و چه ویژگیهایی دارد. در این بخش با بکارگیری نکات بیان شده، به حل چند نمونه مثال میپردازیم.
مثال ۱
ابتدا یک گراف بدون جهت با راس و یال رسم کنید:
- سپس ماتریس مجاورت آن را بنویسید.
- در این ماتریس مجاورت عدد به چه معنا است؟
- این ماتریس مجاورت را به یک لیست مجاورت تبدیل کنید:
پاسخ
دقت کنید برای رسم چنین گرافی میتوان حالتهای دلخواه متفاوتی را در نظر گرفت. اما مهم این است که ماتریس مجاورت آن به درستی نمایش داده شود. ما گراف زیر را در نظر گرفتهایم که دارای چهار راس با شمارههای و و و است و سه یال و و در آن دیده میشود:
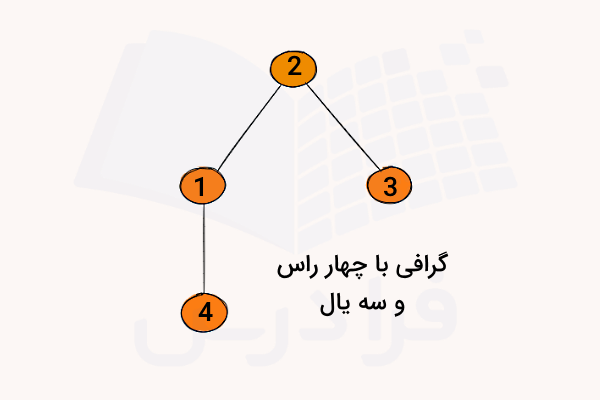
سپس ماتریس مجاورت متناظر با چنین گرافی را به شکل زیر خواهیم داشت، تعداد سطرها و ستونها چهار است و با توجه به اینکه گراف بدون جهت است، ماتریس مجاورت متقارن خواهد بود:
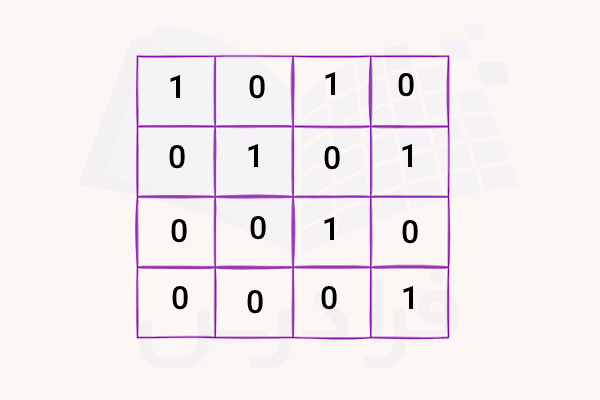
میدانیم در این نمایش مقدار به معنای وجود یال و مقدار به معنای عدموجود یال بین دو راس است. پس یعنی در گراف بدون جهت ما یک یال بین هر دو راس موردنظر وجود دارد یا به بیانی دیگر، آن دو راس مجاور هم هستند. در مورد سوال سوم، لیست مجاورت برای هر راس عبارت است از لیست راسهایی که به آن راس متصلاند. این لیست به شکل زیر است:
- : راس و
- : راس و
- : راس
- : راس
مثال ۲
اگر گراف چندگانهای با مشخصات زیر داشته باشیم، ماتریس مجاورت آن به چه صورت است؟ در ادامه ویژگیهای رئوس آن را بررسی کنید:
راسها:
یالها:
پاسخ
در این گراف چهار راس داریم، پس ماتریس مجاورت ما که یک ماتریس مربعی است، ماتریس چهار در چهاری خواهد بود که با توجه به یالهای داده شده مقادیر عددی درایههای متناظر با این یالها برابر با هستند. همچنین پیش از شروع دقت کنید، یالهایی به شکل و متناظراند با حلقه روی راسهای و . با توجه به اینکه در صورت سوال به جهتدار بودن گراف اشارهای نشده است، بنابراین یالها جهتدار نیستند و لازم است اگر درایه متناظر با را برابر با در نظر میگیریم، درایه متناظر با را نیز فرض کنیم. به این ترتیب ماتریس مجاورت برای این گراف به شکل زیر خواهد شد:
| D | C | B | A | |
| A | ||||
| B | ||||
| C | ||||
| D |
حالا ویژگیهای رئوس را به ترتیب بررسی میکنیم:
- راس : درایه قطر اصلی متناظر با این راس برابر است با . پس روی راس یک حلقه داریم. همچنین مجموع درایههای سطر برابر است با ، اما چون روی این راس یک حلقه داریم، پس اولین دو مرتبه شمرده میشود و درجه راس برابر است با .
- راس : تمام مقادیر روی سطر برابر با صفر هستند. بنابراین درجه این راس نیز برابر است با صفر. به عبارت دیگر، میتوانیم بگوییم راس یک راس جدا افتاده است.
- راس : مجموع درایههای سطر برابر است با و حلقهای نداریم. پس درجه این راس برابر است با .
- راس : درایه قطر اصلی متناظر با این راس برابر است با . پس روی راس یک حلقه داریم. همچنین مجموع درایههای سطر برابر است با ، اما چون روی این راس یک حلقه داریم، پس اولین دو مرتبه شمرده میشود و درجه راس برابر است با .
مثال ۳
فرض کنید گرافی با مشخصات زیر داریم:
راسها:
یالها:
ماتریس مجاورت این گراف به همراه ویژگیهای هر راس آن چگونه است؟
پاسخ
در این گراف پنج راس داریم، پس ماتریس مجاورت ما یک ماتریس مربعی پنج در پنج خواهد بود:
| E | D | C | B | A | |
| A | |||||
| B | |||||
| C | |||||
| D | |||||
| E |
حالا ویژگیهای رئوس را به ترتیب بررسی میکنیم:
- راس : مجموع درایههای سطر برابر است با و حلقهای نداریم. پس درجه این راس برابر است با .
- راس : مجموع درایههای سطر برابر است با و حلقهای نداریم. پس درجه این راس برابر است با .
- راس : مجموع درایههای سطر برابر است با و حلقهای نداریم. پس درجه این راس برابر است با .
- راس : مجموع درایههای سطر برابر است با و حلقهای نداریم. پس درجه این راس برابر است با .
- راس : مجموع درایههای سطر برابر است با و حلقهای نداریم. پس درجه این راس برابر است با .
مقایسه ماتریس مجاورت با سایر روش های نمایش گراف
جدول زیر سه روش اصلی برای نمایش گرافها در علوم کامپیوتر و ریاضیات را مقایسه میکند که عبارتاند از ماتریس مجاورت، لیست مجاورت و ماتریس وقوع یا Incidence Matrix. هر کدام از این روشها مزایا و معایب خاص خود را دارند و همین مسئله موجب شده است که آنها را برای انواع مختلفی از گرافها و الگوریتمها مناسب بدانیم.
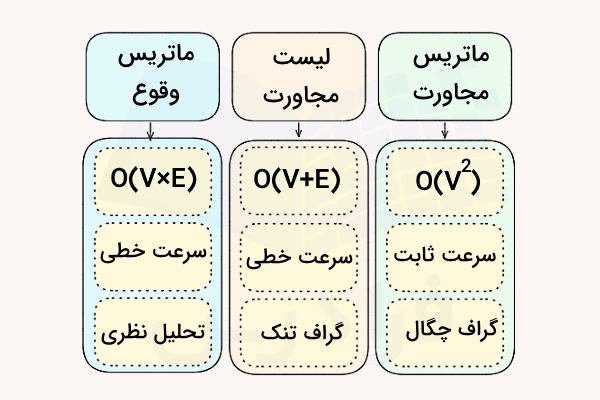
نمایش گراف توسط ماتریس مجاورت
در بخشهای قبل گفتیم که ماتریس مجاورت یک آرایه دو بعدی مربعی به شکل است که در آن تعداد رئوس گراف است. هر درایه در این ماتریس نشاندهنده وجود یا عدموجود یک یال بین راس و راس است. فضای موردنیاز برای کار با این ماتریس فضای است، به این معنا که فضای ذخیرهسازی موردنیاز به شکل مجذور تعداد رئوس رشد میکند.
این روش برای گرافهایی با تعداد رئوس زیاد اما یالهای کم بسیار ناکارآمد است، زیرا بخش زیادی از ماتریس با صفر پر میشود. در همین زمینه اگر تمایل دارید اطلاعات بیشتری بهدست آورید، میتوانید فیلم آموزش ریاضیات گسسته – پایه دوازدهم فرادرس را مشاهده کنید که لینک آن نیز برای دسترسی شما در ادامه قرار داده شده است:
همچنین سرعت یافتن یال در مورد ماتریس مجاورت ثابت است، یعنی داریم و این یکی از بزرگترین مزایای ماتریس مجاورت است. برای بررسی اینکه آیا یالی بین دو راس و وجود دارد یا خیر، کافی است به درایه مراجعه کنیم و این کار در زمان ثابتی انجام میشود. بنابراین این ویژگی برای الگوریتمهایی که نیاز دارند مکررا وجود یال را بررسی کنند، بسیار بهینه است. بیشترین کاربرد برای ماتریس مجاورت در مورد گرافهای چگال است. گراف چگال گرافی است که تعداد یالهای آن به تعداد حداکثر یالهای ممکن نزدیک است. در چنین گرافهایی ماتریس مجاورت فضای ذخیرهسازی را بهخوبی توجیه میکند و سرعت بالای جستجوی یال، آن را به گزینهای عالی تبدیل میکند.
نمایش گراف توسط لیست مجاورت
لیست مجاورت یا Adjacency List آرایهای از لیستها است که در آن هر خانه آرایه (با اندیس ) یک لیست پیوندی دارد که شامل تمام رئوس مجاور با راس است. این روش به جای یک ماتریس بزرگ، از ساختارهای داده پویا استفاده میکند. فضای موردنیاز برای لیست مجاورت به شکل است، به این مفهوم که این روش به مجموع تعداد رئوس و یالها بستگی دارد. این مسئله باعث میشود که لیست مجاورت برای گرافهایی با تعداد یالهای کم بسیار مناسب باشد، زیرا فقط یالهای موجود ذخیره میشوند.
سرعت یافتن یال در مورد لیست مجاورت به شکل خطی، یا است. برای بررسی وجود یال بین دو راس و ، باید لیست مربوط به راس را بهطور کامل جستجو کنیم. در بدترین حالت، این زمان به تعداد یالهای متصل به راس (درجه آن) وابسته است که در نهایت میتواند به یا برسد. به این ترتیب کاربرد لیست مجاورت در مورد گرافهایی با تعداد یالهای کم است. از آنجایی که لیست مجاورت از فضای ذخیرهسازی بهینهتری استفاده میکند و الگوریتمهای پیمایشی مانند BFS و DFS بهطور طبیعی با آن سازگار هستند، این روش انتخاب اول برای اکثر مسائل گراف است.
نمایش گراف توسط ماتریس وقوع
در نهایت ماتریس وقوع یا Incidence Matrix را داریم که یک ماتریس است و در آن تعداد رئوس و تعداد یالها است. یک درایه در این ماتریس نشان میدهد که آیا راس با یال در ارتباط است یا خیر. همچنین فضای موردنیاز در این نوع ماتریس است. بنابراین این روش میتواند به فضای زیادی نیاز داشته باشد، بهویژه در مورد گرافهای بزرگ. سرعت یافتن یال برای ماتریس وقوع خطی یا است. برای یافتن یال بین دو راس، باید کل ماتریس را جستجو کنیم که زمان زیادی میبرد. بنابراین این روش برای اجرای عملیات روزمره روی گراف ناکارآمد است.
در عین حال کاربرد ماتریس وقوع بیشتر در زمینه تحلیلهای نظری و اثباتهای ریاضی در نظریه گراف است و کاربرد عملی آن در الگوریتمها کمتر است. پس انتخاب بین این سه روش به نوع گرافی که با آن سر و کار داریم، بستگی دارد. اگر گراف چگال است (یالهای زیادی دارد)، ماتریس مجاورت به دلیل سرعت بالای جستجوی یال انتخاب بهتری است. اگر گراف تنک است یا یالهای کمی دارد، لیست مجاورت به دلیل کارآمدی در فضای ذخیرهسازی انتخاب برتر است و در عمل، در اکثر مسائل گراف از همین روش استفاده میشود. ماتریس وقوع نیز بیشتر جنبه نظری دارد و کاربردهای عملی آن محدود است.
همچنین پس از اینکه یاد گرفتیم تفاوتهای دو روش دیگر نمایش گراف با ماتریس مجاورت چیست، بهتر است به نکات زیر حتما توجه کنیم:
- فراموش کردن وارد کردن هر دو خانه برای گرافهای بدون جهت.
- فرض اینکه برای گرافهایی با تعداد راس بالا ولی یالهای کم باید از ماتریس مجاورت استفاده شود، در حالی که برای گرافهای تنک بهتر است از لیست مجاورت استفاده کنید.
- اشتباه برچسبگذاری یا Labeling راسها هنگام ساختن ماتریس، به این مفهوم که سعی کنید همیشه از یک ترتیب مشخص و واضح برای شمارهگذاری استفاده کنید.
یادگیری گراف ها و ریاضیات گسسته با فرادرس
یکی از مهمترین مباحث درس ریاضی مقطع متوسطه دوم و بهویژه برای دانشآموزان رشته ریاضی، درس ریاضیات گسسته است. ریاضیات گسسته یا Discrete Mathematics بخشی از علم ریاضی است که به مطالعه ساختارها و عناصر گسسته میپردازد. مباحث مهمی که در ریاضیات گسسته مطرح میشوند عبارتاند از نظریه مجموعهها، ترکیبیات و نظریه گراف که ماتریس مجاروت بخشی از این نظریه محسوب میشود. به همین علت در این بخش میخواهیم چند فیلم آموزشی از مجموعه فرادرس را به شما معرفی کنیم که در تمام آنها بخشی از این مباحث توضیح داده شده است:
- فیلم آموزش رایگان گراف در ریاضیات گسسته
- فیلم آموزش ریاضیات گسسته پایه دوازدهم
- فیلم آموزش ریاضیات گسسته پایه دوازدهم – مرور و حل مساله
ماتریس مجاورت و برنامه نویسی
در این بخش نشان میدهیم در محیطهای برنامهنویسی از جمله پایتون یا ++C، روش استفاده از ماتریس مجاورت چیست. الگوریتمهایی مانند BFS و DFS میتوانند از ماتریس مجاورت برای پیمایش گراف در مسائل کدنویسی استفاده کنند.
مثال ماتریس مجاورت در پایتون
در محیط پایتون میتوانید از کد زیر برای استفاده از ماتریس مجاورت استفاده کنید:
# n = number of nodes adj_matrix = [[0 for _ in range(n)] for _ in range(n)] # Add an edge from node i to node j adj_matrix[i][j] = 1مثال ماتریس مجاورت در ++C
همچنین در سی پلاس پلاس نیز کد زیر در زمینه محاسبه ماتریس مجاورت به شما کمک خواهد کرد:
// n = number of nodes vector<vector> adj_matrix(n, vector(n, 0)); // Add an edge from node i to node j adj_matrix[i][j] = 1;سایر کاربردهای ماتریس مجاورت
در انتهای این مطلب از مجله فرادرس، کاربردهای ماتریس مجاورت را با هم مرور میکنیم. بهطور کلی بخش عمدهای از کاربرد این نوع ماتریس در نظریه گراف و علوم کامپیوتر است. برای مثال محاسبات مربوط به تحلیل اتصالپذیری، درجه رئوس (تعداد یالهای متصل به یک راس که با جمع زدن یک سطر یا ستون به دست میآید) و یافتن مسیر در نظریه گراف را میتوان با استفاده از ماتریس مجاورت انجام داد.
همچنین در حوزههایی از علوم کامپیوتر مانند نمایش شبکه، پیادهسازی الگوریتمهای گراف و تحلیل روابط در ساختارهای داده میتوان مفاهیم و محاسبات ماتریس مجاورت را بکار برد. بنابراین ماتریس مجاورت فقط در ریاضیات کاربرد ندارد، بلکه نقش مهمی در علم فیزیک (تحلیل شبکه)، علوم کامپیوتر (الگوریتمهای گراف مانند BFS و DFS) و حتی استدلال منطقی در زندگی روزمره ایفا میکند.












