لگاریتم و خصوصیات آن — به زبان ساده

در ریاضیات و جبر، خصوصیات زیادی برای عملگرهای مختلف وجود دارد. برای مثال خاصیت جابجایی برای عمل جمع نشان می‌دهد که ترتیب قرارگیری اعداد در نتیجه عمل جمع تاثیرگذار نیست. یا خاصیت پخشی ضرب در جمع نیز از این جمله‌اند. در این متن به تابع لگاریتم و خصوصیات آن خواهیم پرداخت. هر چند ممکن است که گستردگی کاربرد تابع لگاریتم، به میزان عمل جمع و ضرب نباشد، ولی در بسیاری از موارد، عملیات ضرب توسط لگاریتم ساده‌تر صورت می‌گیرند.

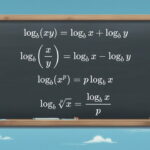
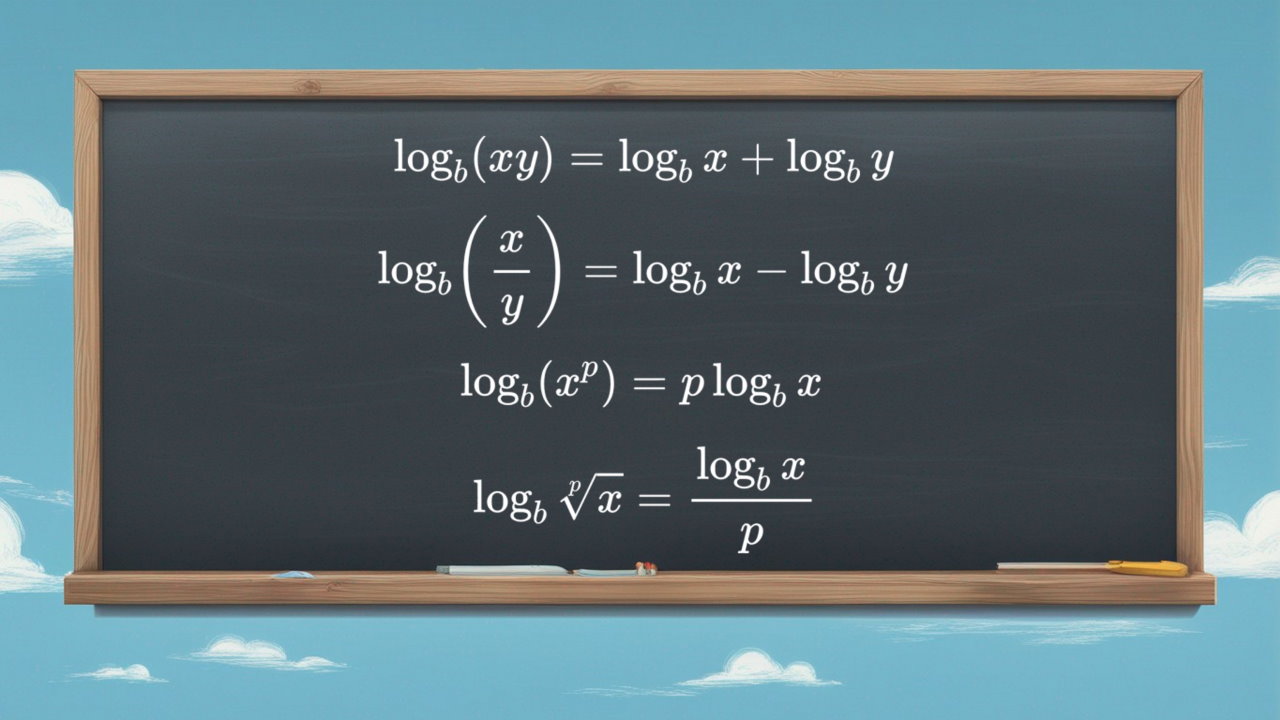
برای آشنایی با تابع لگاریتم و نحوه محاسبه و کاربردهای آن بهتر است مطلب لگاریتم و هر آنچه باید درباره‌ آن بدانید – به زبان ساده و کاربرد لگاریتم — به زبان ساده را مطالعه کنید. از آنجایی که تابع لگاریتم معکوس تابع نمایی است، آگاهی از خصوصیات تابع نمایی نیز در درک ویژگی‌های تابع لگاریتم موثر است. بنابراین خواندن نوشتار ویژگی های تابع نمایی — به زبان ساده نیز خالی از لطف نیست.

لگاریتم و خصوصیات آن

شاید بتوان انگیزه اصلی برای ایجاد تابع لگاریتم (یا عملگر لگاریتم) را ساده کردن عملیات پیچیده ضرب در نظر گرفت. از طرفی لگاریتم‌گیری از اعداد، مقیاس آن‌ها را کوچکتر می‌کند. در نتیجه به نظر می‌رسد علت بوجود آمدن مفهومی به نام لگاریتم برای ساده‌سازی عملیات با مقادیر بزرگ صورت گرفته است.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

در سال 1614 میلادی «جان نپر» (John Napier) دانشمند اسکاتلندی، واژه لگاریتم را برای عملگر ابداعی خودش به کار برد که به صورت عکس عمل توان یا ضرب‌های متوالی محاسبه می‌شد. البته قبل از او نیز دانشمندان دیگر در زمینه لگاریتم و خصوصیات آن فعالیت‌هایی داشته‌اند ولی اولین بار جان نپر نام لگاریتم را استفاده کرد. به طور معمول تعریفی که از عملگر لگاریتم در حساب و جبر به کار می‌رود، ساده کردن حاصل ضرب توان‌هایی از عدد ۱۰ است. به این ترتیب لگاریتم را برمبنای ۱۰ می‌نامند. البته اگر این ضرب‌ها را برمبنای عدد دیگری در نظر بگیریم، مبنای لگاریتم را هم تغییر داده‌ایم. یکی دیگر از عملگرهای این چنینی، لگاریتم برمبنای عدد نپر است که به آن لگاریتم طبیعی نیز گفته می‌شود. لگاریتم برمبنای ۲ نیز کاربردهای خود را بخصوص در محاسبات دو دویی (دیجیتالی) دارد. برای روشن شدن موضوع به چند مثال توجه کنید.

نکته: دقت داشته باشید که با توجه به ارتباطی که بین توان و لگاریتم وجود دارد، برای اعداد منفی لگاریتم تعریف نشده است.

مثال ۱

می‌توانیم عدد ۱۰۰ را به صورت حاصل ضرب ۱۰ در ۱۰ بنویسیم:

$$\large 100 = 10 \times 10 = 10^2$$

تعداد این ضرب‌ها (یا توانی از ۱۰) که عدد ۱۰۰ را تولید کند برابر با ۲ است در نتیجه خواهیم داشت:

$$\large \log_{10}(100)=2$$

مشخص است که در اینجا مبنای لگاریتم عدد ۱۰ است که به صورت اندیس در زیر عملگر $$\log$$ قرار گرفته است. به این ترتیب می‌گوییم، لگاریتم عدد ۱۰۰ برمبنای ۱۰ برابر است با ۲.

نکته: لگاریتم هر عدد بر مبنای خود برابر با ۱ خواهد بود زیرا تساوی زیر برای هر عدد نامنفی برقرار است:

$$\large a= a^1\; \rightarrow \log_a a =1$$

مثلا، لگاریتم ۱۰ برمبنای ۱۰ برابر است با ۱.

مثال ۲

عدد ۳۲ را می‌توان به صورت حاصل‌ضرب متوالی ۲ به صورت زیر نوشت:

$$\large 32= 2 \times 2\times 2 \times 2 \times 2 = 2^5$$

با توجه به اینکه عمل ضرب عدد ۲، به تعداد پنج‌ بار صورت گرفته است، می‌توانیم بگوییم که لگاریتم عدد ۳۲ برمبنای ۲ برابر با ۵ است و بنویسیم:

$$\large \log_2 32 = 5$$

مثال ۳

عدد $$e^4$$ را در نظر بگیرید. در اینجا منظور از $$e$$ عدد نپر (عدد اویلر) است که متعلق به مجموعه اعداد اصم (گنگ) بوده و مقدار تقریبی آن 2٫۷۱۸۲ است. بر این اساس می‌توانیم بگویم که لگاریتم عدد  $$e^4$$ برمبنای $$e$$ نیز برابر است با ۴ و آن را به صورت زیر نمایش دهیم:

$$\large \log_{e}e^4=4$$

لگاریتم برمبنای $$e$$ را به صورت $$\ln$$ نیز نشان می‌دهند در نتیجه عبارت بالا را به صورت زیر می‌نویسیم:

$$\large \ln e^4=4$$

مشخص است که در عملگر $$\ln$$ دیگر مبنای لگاریتم نوشته نمی‌شود زیرا مشخص است که مبنا عدد $$e$$‌ است.

نکته: گاهی به مبنای لگاریتم، پایه لگاریتم نیز می‌گویند زیرا مبنای لگاریتم همان پایه تابع نمایی است. در مثال ۱، عدد ۱۰ پایه توان $$10^2$$‌ است و همینطور مبنا یا پایه لگاریتم $$\log_{10}(100)$$ نیز محسوب می‌شود.

مثال ۴

لگاریتم ۱۵۰ برمبنای ۱۰ بین ۲ و ۳ قرار دارد زیرا رابطه زیر بین توان‌های ۱۰ برقرار است:

$$\large 10^2=100 < 150 <10^3$$

پس

$$\large \log_{10}(100)=2 < \log_{10}(150) <3=\log_{10}(1000)$$

مثال ۵

لگاریتم اعداد کوچکتر از یک، منفی هستند. برای مثال لگاریتم $$\frac{1}{2}$$ را به صورت زیر می‌توانیم محاسبه کنیم.

$$\large {\displaystyle \quad \log _{2}\!{\frac {1}{2}}=\log_22^{-1}=-1\quad }$$

زیرا

$$\large {\displaystyle \quad 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}}$$

رابطه معکوس لگاریتم

ابتدا اشاره کردیم که عمل به توان رساندن با لگاریتم در ارتباط است. طبق تعریفی که از لگاریتم ارائه کردیم می‌توانیم این ارتباط را به صورت زیر نمایش دهیم.

$$\large {\displaystyle \log _{b}\left(b^{x}\right)=x\log _{b}b=x}$$

این رابطه بیان می‌کند که ترکیب دو تابع لگاریتم و تابع نمایی، یک تابع همانی است. این مسئله نشان می‌دهد که تابع لگاریتم معکوس تابع نمایی است و البته تابع نمایی نیز معکوس تابع لگاریتم محسوب می‌شود.

در این قسمت با لگاریتم و خصوصیات اصلی آن آشنا شدیم. در ادامه به معرفی دیگر ویژگی‌های لگاریتم در ارتباط با عملگرهای دیگر خواهیم پرداخت.

نکته: توجه داشته باشید که لگاریتم هر عدد برمبنای خودش برابر با ۱ است.

$$\large  a^1=a \rightarrow \log_a(a)=1$$

رابطه بین ضرب و جمع در لگاریتم و خصوصیات آن

با توجه به ارتباطی که بین عملگر توان و لگاریتم وجود دارد، می‌توان خصوصیاتی که برای توان داریم را به لگاریتم نیز تعمیم دهیم.

فیلم آموزش تبدیل لگاریتمی و تفاضل گیری در پیش پردازش سری های زمانی (رایگان) در فرادرس

کلیک کنید

فرض کنید دو عدد A و B داریم که می‌توانیم آن‌ها را به صورت زیر بنویسیم:

$$\large A=a^x, \;\;\; B=a^y$$

حاصلضرب این دو عدد به صورت زیر نوشته خواهد شد.

$$\large A\times B= a^x \times a^y = \overbrace{a \times \cdots \times a}^x \times \overbrace{a \times \cdots \times a}^y= a^{(x+y)}$$

با توجه به اینکه پایه همه این توان‌ها، برابر است، می‌توانیم مبنای لگاریتم را هم $$a$$ در نظر بگیریم. پس

$$\large \log_a{A\times B}= x+y=\log_aA+\log_aB$$

به این ترتیب می‌توان گفت:

لگاریتم حاصلضرب دو عدد، برابر است با حاصل جمع لگاریتم آن‌ها

مثال ۶

لگاریتم عدد ۲۴۳ را بر مبنای ۳ می‌توان براساس حاصل‌ضرب لگاریتم اعداد ۳ و ۹ برمبنای ۳ به صورت زیر نوشت:

$$\large {\displaystyle \log _{3}243=\log _{3}(9\times 27)=\log _{3}9+\log _{3}27=2+3=5}$$

نکته: در عملگر توان می‌دانیم که توان منفی به معنی تقسیم یا معکوس یک عدد است. برای مثال $$x^{-1}=\frac{1}{x}$$ و یا $$x^{-3}=\frac{1}{x^3}$$ است. از این خاصیت برای لگاریتم تقسیم دو عدد نیز می‌توان استفاده کرد.

مثال ۷

لگاریتم عدد ۱۶ برمبنای ۲ را می‌توان به صورت زیر بدست آورد:

$$\large {\displaystyle \log _{2}16=\log _{2}\!{\frac {64}{4}}= \log_2 (64 \times 4^{-1})=\log _{2}64-\log _{2}4=6-2=4}$$

مشخص است که لگاریتم تقسیم دو عدد به صورت تفاضل لگاریتم مخرج از صورت بدست می‌آید. به این ترتیب لگاریتم و خصوصیات آن در رابطه با ضرب و تقسیم مورد بررسی قرار گرفت.

لگاریتم تقسیم دو عدد یا یک کسر، برابر است با، لگاریتم عدد صورت منهای لگاریتم عدد مخرج کسر

رابطه توان و جذر در لگاریتم و خصوصیات آن

فرض کنید عدد مثبت $$A$$ به توان $$p$$ رسیده باشد. حاصل لگاریتم $$A^p$$ بر مبنای $$b$$ به صورت زیر قابل محاسبه است (فرض کنید $$p$$ یک عدد طبیعی باشد).

$$\large \log_b A^p = \log_b (\overbrace {A \times \cdots A}^p)=\overbrace{\log_2A+\cdots+\log_2A}^p=p\log_bA$$

مثال ۸

لگاریتم ۶۴ برمبنای ۲ را می‌توان به صورت زیر محاسبه کرد:

$$\large {\displaystyle \log _{2}64=\log _{2}\left(2^{6}\right)=6\log _{2}2=6}.$$

از آنجایی که بین توان و جذر نیز رابطه‌ای وجود دارد، لگاریتم جذر یک عدد را نیز می‌توان مطابق با مثال زیر بدست آورد.

مثال ۹

لگاریتم ریشه دوم ۱۰۰۰ براساس رابطه زیر برابر با 1٫5 خواهد بود.

$$\large {\displaystyle \log _{10}{\sqrt {1000}}=\log_{10}(1000)^{\frac{1}{2}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$$

به این ترتیب می‌توان گفت:

لگاریتم توان یک عدد برابر است با حاصل ضرب توان در لگاریتم آن عدد

جدول زیر به منظور خلاصه‌سازی خصوصیات ضرب، تقسیم، توان و ریشه لگاریتم اعداد تهیه شده است.

جدول ۱

به این ترتیب لگاریتم و خصوصیات آن در رابطه با ضرب و تقسیم مورد بررسی قرار گرفت.

تغییر مبنا در لگاریتم و خصوصیات آن

گاهی در انجام محاسبات لگاریتمی، لازم است که مبنای لگاریتم تغییر کند از رابطه زیر برای تغییر مبنای لگاریتم $$x$$ از $$k$$ به $$b$$ می‌توانید استفاده کنید.

$$\large {\displaystyle \log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.\,}$$

برای نشان دادن این موضع، فرض کنید لگاریتم $$x$$ برمبنای $$b$$ برابر با $$y$$‌ باشد.

$$\large \log_b x = y\; \rightarrow\; b^y=x$$

پس داریم

$$\large \log_k x = \log_k b^y= y \log_k b$$

از طرفی $$y=\log_b x$$ پس

$$\large y = \log_b x= \dfrac{\log_k x}{\log_k b}$$

به این ترتیب می‌توانیم لگاریتم یک عدد را برحسب مبنای ۱۰ یا لگاریتم طبیعی به صورت زیر بدست آوریم.

$$\large {\displaystyle \log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}}$$

مثال ۱۰

لگاریتم ۱۰۰ برمبنای ۲ برابر است با تقسیم لگاریتم ۱۰۰ برمبنای ۱۰ و لگاریتم ۲ برمبنای ۱۰، یعنی

$$\large \log_2 100 = \dfrac{\log_{10} 100}{\log_{10} 2}=\dfrac{2}{0.3}=6.64$$

نکته: یکی دیگر از ویژ‌گی‌های لگاریتم را می‌توان به صورت زیر نوشت:

$$x = a ^ { \log ^x _ a }$$

مثال ۱۱

لگاریتم عدد ۱۰۰ برمبنای نامشخصی برابر است با ۲، پس می‌توانیم مبنا را به کمک رابطه بالا بدست آوریم.

$$$$x = a ^ { \log ^x _ a }\\ \log ^ { 100 = x } _ a = 2 \\ 100 = a ^ { \log ^ { 100 } _ 2 } = a ^ 2 \\ 10 ^ 2 = a ^ 2 \rightarrow a = 10

تابع لگاریتم و خصوصیات آن

در ادامه موضوع محاسبه لگاریتم یک عدد، حال می‌خواهیم با تابع لگاریتم بیشتر آشنا شویم.

$$\large f(x)=\log_k(x), \;\;x\geq 0$$

تابع $$f(x)$$ در اینجا به صورت لگاریتم یک عدد نامنفی مشخص شده است. همانطور که دیده می‌شود، دامنه این تابع مجموعه مقادیر نامنفی از اعداد حقیقی است. با توجه به نحوه محاسبه لگاریتم، برد این تابع نیز اعداد حقیقی خواهد بود. زیرا

$$\large \log_k(0)=undifine,\;\;\; \log_k(+\infty)=+\infty$$

نمودار مربوط به این تابع در تصویر زیر دیده می‌شود.

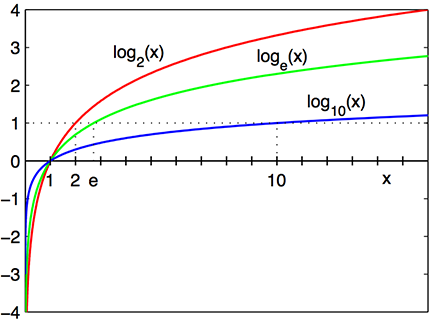
شکل ۱: نمودار تابع لگاریتم براساس مبناهای مختلف

همانطور که مشخص است، زمانی که مقدار روی محور افقی، از یک کوچکتر باشد، مقدار لگاریتم (روی محور عمودی) منفی خواهد شد. تابع لگاریتم یک تابع مقعر (Concave) محسوب می‌شود درست برعکس تابع نمایی (Exponential Function) که تابعی محدب (Convex) است. اغلب تابع لگاریتم را به عنوان تابع معکوس (Inverse Function) تابع نمایی در نظر می‌گیرند.

تابع لگاریتم با توجه به نمودارهای ترسیم شده، تابعی صعودی از $$x$$ است اگر مبنای آن بزرگتر از ۱ باشد.

$$\large x_1, x_2 \in D_f,\; x_11$$

همچنین این تابع برای مقادیر مبنای کوچکتر از ۱، نزولی خواهد بود.

$$\large x_1, x_2 \in D_f,\;x_1 \log_k(x_2), \;\;0$$

برای مثال، لگاریتم ۱0۰ برمبنای 10 برابر است با ۲ و لگاریتم ۱۰ برمبنای 10 نیز برابر است با 1، ولی لگاریتم $$100$$ برمبنای $$\frac{1}{2}$$ برابر است با $$-2.86$$ در حالیکه لگاریتم ۱۰ برمبنای $$\frac{1}{2}$$ برابر است با $$-1.43$$ که از مقدار لگاریتم ۱۰۰ برمبنای $$\frac{1}{2}$$ بزرگتر است.

نکته: اگر جای مبنا و متغیر را در لگاریتم عوض کنیم، مقدار لگاریتم معکوس می‌شود. به این ترتیب خواهیم داشت:

$$\large \log_a{x} = \dfrac{1}{\log_x(a)}$$

زیرا اگر فرض کنیم که $$\log_a x=A$$ و $$\log_x a=B$$ آنگاه رابطه‌های زیر برقرار است:

$$\large \log_ax=A, \rightarrow a^A=x$$

$$\large \log_xa=B, \rightarrow x^B=a$$

پس می‌توانیم بنویسیم:

$$\large a^A\times x^B=x\times a$$

در نتیجه برای این که تساوی بالا برقرار باشد، توان‌های $$a$$ در هر دو طرف تساوی باید یکسان باشند. همین موضوع هم باید برای $$x$$ صادق باشد. بنابراین باید $$A=1$$ و $$B=1$$ در نظر گرفته شوند. به این ترتیب حاصل ضرب $$A$$ و $$B$$ هم باید برابر با ۱ شده و براین اساس خواهیم داشت:

$$\large \log_a x \times \log_xa =1 \rightarrow \log_ax = \dfrac{1}{\log_xa}$$

نحوه محاسبه لگاریتم

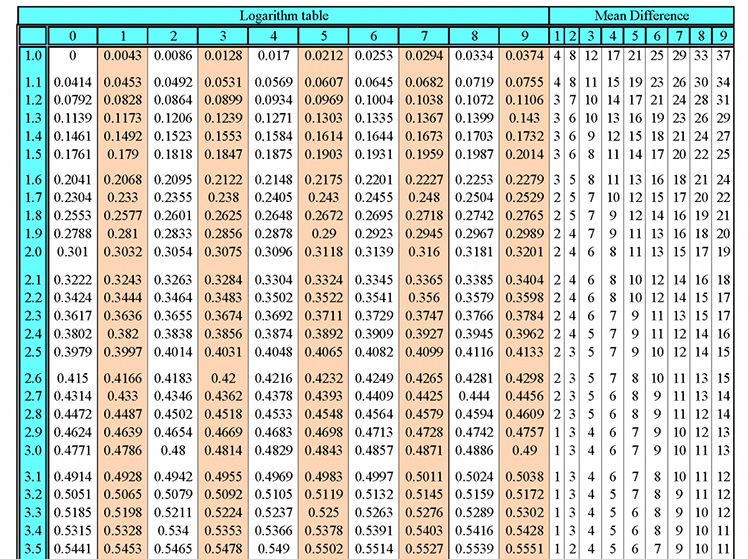
در گذشته برای محاسبه لگاریتم اعداد از جدول‌های لگاریتمی که قبلا محاسبه و منتشر شده بود استفاده می‌کردند ولی بعدها از خط‌کش محاسباتی لگاریتمی، برای این گونه محاسبات بهره گرفتند. امروزه محاسبه لگاریتم با استفاده از ماشین حساب بسیار ساده شده است.

فیلم آموزش تابع در حل مسائل ریاضی دبیرستان با میپل Maple (رایگان) در فرادرس

کلیک کنید

به این ترتیب می‌توانیم لگاریتم و خصوصیات آن را مورد بررسی قرار دهیم.

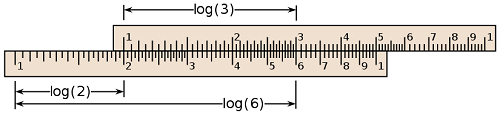
آنچه که در لگاریتم و خصوصیات آن مهم است، تغییری است که این تابع، روی اعداد صورت می‌دهد و موجب فشردن شدن مقیاس آن‌ها می‌شود.. با توجه به نموداری که برای تابع لگاریتم در شکل ۱ وجود دارد، مشخص است که همیشه برای مبناهای بزرگتر از یک، مقدار لگاریتم یک عدد از خود عدد کوچکتر است، پس به نظر می‌رسد که عملگر لگاریتم، باعث تغییر مقیاس اعداد می‌شود. به این ترتیب برای نمایش اعداد خیلی بزرگ یا ترسیم آن‌ها روی نمودارها، می‌توان از تغییر مقیاس لگاریتمی استفاده کرد.

خلاصه و جمع‌بندی

در این نوشتار با نحوه محاسبه لگاریتم و خصوصیات آن آشنا شدیم. ارتباط بین ضرب و تقسیم برای لگاریتم و همچنین تغییر مبنای لگاریتم نیز مورد بحث واقع شد. با ارائه مثال‌هایی در این زمینه‌ها، موضوعات مربوط به لگاریتم واضح‌تر ارائه شدند و مفاهیم مربوط به آن مورد بررسی قرار گرفتند. همانطور که دیدید، استفاده از روابط لگاریتم و خصوصیات آن، باعث می‌شود بسیاری از محاسبات ساده‌تر انجام شوند.