اعداد برنولی و خصوصیات آن | به زبان ساده

در نوشتارهای دیگر مجله فرادرس با «مجموعه اعداد گویا» (Rational Numbers) و همچنین ویژگی آنها آشنا شدهاید. نوع خاصی از اعداد گویا به نام اعداد برنولی وجود دارند که ویژگیهای جالبی داشته و در بسیاری از شاخههای دیگر علوم مانند فیزیک به کار میروند. به همین علت این مطلب را به اعداد برنولی و خصوصیات آن اختصاص دادهایم.
به منظور آشنایی بیشتر با مباحث مطرح شده در این حوزه، بهتر است مطالب چند جملهایها — به زبان ساده و تابع زتای ریمان — از صفر تا صد را مطالعه کنید. همچنین خواندن نوشتارهای سری بینهایت — به زبان ساده و رابطه بازگشتی — از صفر تا صد نیز خالی از لطف نیست.
اعداد برنولی و خصوصیات آن
در ریاضیات، «اعداد برنولی» (Bernoulli Numbers) که با نماد $$B_n$$ نمایش داده میشوند، دنبالهای از اعداد گویا هستند که اغلب در نظریه اعداد به کار میروند. اعداد برنولی را میتوان در بسط یا دنباله تابع «تانژانت» (Tangent) و «تانژانت هایپربولیک» (Hyperbolic Tangent) مشاهده کرد. همچنین در مجموع توان $$m$$ام اعداد صحیح مثبت نیز از اعداد برنولی صحبت به میان میآید. از طرفی در «تابع زتای ریمان» (Riemann Zeta Function) نیز با اعداد برنولی برخورد خواهیم کرد.
در جدول زیر، ۲۰ عدد اول برنولی را مشاهده میکنید. واضح است که این مقادیر هم میتوانند مثبت باشند و هم منفی، ولی به هر حال به صورت یک کسر بیان میشوند.
| n | کسر | عدد برنولی |
| 0 | $$1$$ | +1.000000000 |
| 1 | $$ \pm \frac{1}{2} $$ | ±0.500000000 |
| 2 | $$ \frac{1}{6} $$ | +0.166666666 |
| 3 | $$0$$ | +0.000000000 |
| 4 | $$−\frac{1}{30}$$ | −0.033333333 |
| 5 | $$0$$ | +0.000000000 |
| 6 | $$\frac{1}{42}$$ | +0.023809523 |
| 7 | $$0$$ | +0.000000000 |
| 8 | $$−\frac{1}{30}$$ | −0.033333333 |
| 9 | $$0$$ | +0.000000000 |
| 10 | $$\frac{5}{66}$$ | +0.075757575 |
| 11 | $$0$$ | +0.000000000 |
| 12 | $$−\frac{691}{2730}$$ | −0.253113553 |
| 13 | $$0$$ | +0.000000000 |
| 14 | $$\frac{7}{6}$$ | +1.166666666 |
| 15 | $$0$$ | +0.000000000 |
| 16 | $$−\frac{3617}{510}$$ | −7.092156862 |
| 17 | $$0$$ | +0.000000000 |
| 18 | $$\frac{43867}{798}$$ | +54.97117794 |
| 19 | $$0$$ | +0.000000000 |
| 20 | $$−\frac{174611}{330}$$ | −529.1242424 |
همانطور که در جدول بالا مشاهده میکنید، فقط عدد برنولی $$B_1$$ است که هم علامت مثبت داشته و هم منفی. ترتیب علامتها در اعداد برنولی $$ n \geq 3$$ به صورت، صفر، منفی، صفر و مثبت است. به این معنی که برای $$n>1$$ و فرد، مقدار عدد برنولی صفر است. سپس اعداد برنولی به صورت تناوبی تغییر علامت داده و برای اعداد برنولی با $$n$$ زوج، یکی در میان منفی و مثبت هستند.
این خاصیت را میتوان به این صورت نیز در نظر گرفت که برای $$n$$های زوج، اگر $$n$$ بر چهار بخشپذیر باشد، مقدار عدد برنولی منفی و در غیر اینصورت مثبت است. برای مثال $$B_4 = -0.03333$$ و $$B_6 = +0.02380$$.
نکته: از آنجایی که $$B_n$$ها برای مقادیر فرد $$n$$، برابر با صفر هستند، گاهی اعداد برنولی را با نماد $$B_{2n}$$ نشان میدهند.
تاریخچه اعداد برنولی
اعداد برنولی ریشه در تاریخ قدیم دارند، جایی که ریاضیدانان میخواستند مجموع اعداد صحیح تواندار را بدست آورند. مجموع $$n$$ عدد اول صحیح، مجموع مربعات یا مکعب آنها ذهن دانشمندان عصر قدیم را به خود مشغول کرده بود. ولی در این بین فرمولی که بتواند برای همه آنها چاره ساز باشد، کشف نشد.
در بین دانشمندانی مانند الکرجی، فرما و پاسکال، تنها «ژاکوب برنولی» (Jakob Bernoulli) بود که توانست یک فرمول برای بدست آوردن مجموع توانهای $$n$$ عدد اول صحیح بدست آورد. او دنبالهای به صورت $$B_0, B_1, B_2 , \cdots$$ یافت که میتوانستند مجموع توانهای اعداد صحیح را مشخص کنند.
فرمول برنولی برای جمع توانی، مفیدترین و قابل تعمیمترین فرمول تا به امروز است. ضرایب موجود در فرمول برنولی به دنبال پیشنهادی از «آبراهام د مویر» (Abraham de Moivre)، اعداد برنولی نامیده شد. طبق اعداد برنولی، مجموع اعداد صحیح تواندار به صورت زیر محاسبه میشود.
$$ \large {\displaystyle \sum_{k = 1 }^{ n } k^{c} = { \frac {n^{c + 1}}{c + 1}} + {\frac {1}{2}}n^{c} + \sum _{k = 2}^{c}{ \frac {B_{ k }}{ k !}}c^{ \underline {k - 1}}n^{c - k + 1 }} $$
که در آن $$B_1 = \frac{1}{2}$$ است. همچنین نماد $$c^{\underline{k−1}}$$ نیز نشانگر «فاکتوریل نزولی» (Falling Factorial) است که برای «چند جملهایها» (Polynomials) صورت زیر نوشته میشود.
$$ \large {\displaystyle (x)_{n} = x^{\underline {n}} = x(x - 1)(x - 2) \cdots (x - n + 1 ) = \prod _{k = 1}^{n}(x - k + 1 ) = \prod _{ k = 0 }^{n - 1}(x - k)} $$
نکته: در محاسبه جمع اعداد تواندار صحیح، مقدار $$c^{\underline{−1}}$$ برابر با $$\frac{1}{c+1}$$ است. بنابراین میتوانیم فرمول برنولی را به صورت زیر بنویسیم:
$$\large {\displaystyle \sum_{k = 1}^{n}k^{c} = \sum_{k = 0}^{c}{\frac {B_{k}}{k!}}c^{\underline {k-1}}n^{ c - k + 1 }}$$
بطوری که $$B_1 = \frac{1}{2}$$ است. البته برای محاسبه $${\displaystyle \textstyle \sum _{k=1}^{n}k^{9}}$$ یک خطا وجود دارد، بطوری که باید در بخش اول فرمول داشته باشیم $$-\frac{3}{20}n^2$$ در حالیکه در فرمول بالا نتیجه به شکل $$-\frac{1}{12}n^2$$ بدست میآید.
تعریف اعداد برنولی
در زمانی که اعداد برنولی معرفی شدند، روشهای متعدد و مختلفی برای تعریف آنها ابداع شد. در این بخش فقط به سه روش معمول یعنی روش «معادله بازگشتی» (Recursive Equation)، «فرمول صریح» (Explicit Formula) و روش «تابع مولد» (Generating Function) برای تعریف اعداد برنولی میپردازیم.
تعریف اعداد برنولی به روش معادله بازگشتی
اعداد برنولی در رابطه زیر صدق میکنند.
$$ \large {\displaystyle {\begin{aligned} \sum_{k = 0}^{m}{\binom {m + 1}{k}}B_{k}^{- {}}& =\delta_{m,0}\\\sum_{k = 0}^{m}{\binom {m + 1}{k}} B_{k}^{+{}} & = m + 1 \end{aligned}}}$$
البته واضح است که در فرمول اخیر، عدد صحیح $$m$$ مقادیر $$m = 0 ,1,2,\ldots$$ را گرفته و $$\delta$$ هم بیانگر «دلتای کرونکر» (Kronecker Delta) است. حل این معادلات براساس $$B^{\mp}_m$$ منجر به رابطه بازگشتی زیر خواهد شد.
$$ \large {\displaystyle {\begin{aligned}B_{m}^{-{}} & = \delta _{m,0} - \sum_{k = 0 }^{m - 1}{\binom{m}{k}}{\frac{B_{k}^{-{}}}{m - k + 1 }} \\ B_{m}^{+} & = 1 - \sum_{k = 0}^{m - 1}{\binom{m}{k}}{\frac{B_{k}^{+}}{ m - k + 1 }}\end{aligned}}}$$
تعریف اعداد برنولی با فرمول صریح
در سال ۱۸۹۳، «لویس سالشوتز» (Louis Saalchutz)، تقریبا ۳۶ فرمول صریح برای اعداد برنولی معرفی کرد. یکی از آنها که بیشتر مورد استفاده قرار میگیرد، به صورت زیر نوشته میشود.
$$ \large {\displaystyle {\begin{aligned}B_{m}^{-{}}& = \sum_{k=0}^{m}\sum_{v =0}^{k}(-1)^{v}{\binom{k}{v}}{\frac {v^{m}}{k + 1}}\\ B_{m}^{+}& = \sum_{k = 0}^{m}\sum _{v = 0}^{k}(-1)^{v}{\binom {k}{v}}{\frac {(v + 1)^{m}}{k + 1}}\end{aligned}}}$$
تعریف اعداد برنولی به روش تابع مولد
توابع مولد نمایی برای اعداد برنولی به صورت زیر نوشته میشوند.
$$ \large{\displaystyle {\begin{aligned}{ \frac {t}{e^{t} - 1}} & = { \frac {t}{2}} \left( \operatorname {coth} {\frac {t}{2}} - 1 \right) = \sum_{m = 0}^{\infty }{ \frac {B_{m}^{ - {}}t^{m}}{m!}} \\{\frac {t}{1 - e^{-t}}} & = {\frac{t}{2}} \left( \operatorname {coth} {\frac {t}{2}} + 1 \right) = \sum_{m = 0}^{\infty }{ \frac {B_{m}^{+}t^{m}}{m!}} \end{aligned}}}$$
به این ترتیب تابع مولد، به شکل زیر خواهد بود.
$$ \large {\displaystyle z^{- 1} \psi_{1} (z^{- 1}) = \sum_{m = 0}^{\infty }B_{m}^{+}z^{m} } $$
رابطه بالا، یک دنباله نامتناهی و مجانبی برای اعداد برنولی ارائه میکند. واضح است که $$\Phi_1$$، «تابع تریگاما» (Trigamma Function) است که به صورت مشتق دوم از لگاریتم «تابع گاما» (Gamma Function) تعریف میشود.
اعداد برنولی و تابع زتای ریمان
اعداد ریمان را به وسیله عبارتهایی برحسب «تابع زتای ریمان» ( Riemann zeta function) نیز میتوان نوشت. به رابطه زیر توجه کنید.
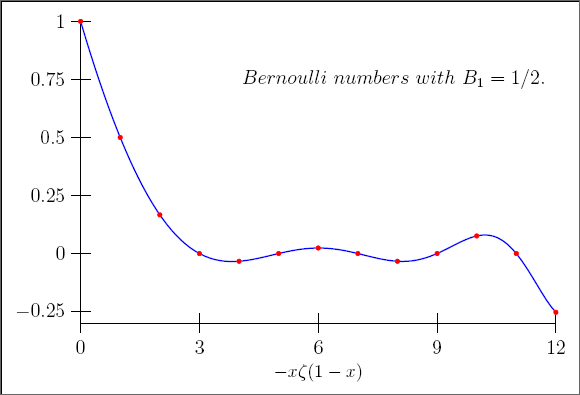
$$ \large B^{+}_ {n} = − n\zeta (1 − n),\;\; \forall n ≥ 1$$
در اینجا پارامتر تابع زتا، صفر یا منفی است. به کمک معادله تابعی زتا و تابع فرمول انعکاسی گاما رابطه زیر حاصل میشود.
$$ \large { \displaystyle B_{2n} = {\frac {(-1)^{n + 1}2(2n)!}{(2 \pi)^{2n}}}\zeta (2n)}, \;\; \forall n ≥ 1$$
در این حالت پارامتر تابع زتا، مثبت خواهد شد. با بزرگتر شدن $$n$$ یا میل کردن $$n$$ به بینهایت، تابع زتا هم به مقدار ۱ میل کرده و طبق «فرمول استرلینگ» (Stirling's Formula)، به رابطه زیر خواهیم رسید.
$$ \large {\displaystyle |B_{2n}| \sim 4{\sqrt {\pi n}} \left({\frac {n}{\pi e}} \right)^{2n}} , \;\; n \to \infty $$
نکته: فرمول استرلینگ یک مقدار تقریبی برای فاکتوریل ارائه میدهد. رابطه زیر نشانگر این تقریب است.
$$\large {\displaystyle n! \sim e^{n\ln n} n {\sqrt {\frac { 2\pi }{n}}}e^{ - n} = { \sqrt {2\pi n}} \left( {\frac {n}{e}} \right) ^{n} }$$
کاربرد اعداد برنولی
هر چند اعداد برنولی در بسیاری از محاسبات و تقریبهای ریاضیاتی، نقش مهمی دارند ولی در این قسمت به دو کاربرد اعداد برنولی در زمینه محاسبه مجموع اعداد تواندار و همچنین «بسط تیلور» (Tailor Expansion) توابع مثلثاتی میپردازیم.
مجموع عبارتهای توانی و اعداد برنولی
مجموع $$n$$ عدد اول صحیح را که به توان $$m$$ رسیدهاند را در نظر بگیرید. واضح است که $$m , n \geq 0$$ هستند. این جمع را به صورت زیر نشان میدهیم.
$$\large {\displaystyle S_{m}(n) = \sum _{k = 1}^{n}k^{m} = 1^{m} + 2^{m} + 3^{m} +\cdots + n^{m}}$$
این رابطه را میتوان به صورت چند جملهای برحسب $$n$$ با درجه یا مرتبه $$m+1$$ نوشت. ضرایب این چند جملهای با اعداد برنولی بوسیله فرمول برنولی و به شکل زیر در ارتباطند.
$$\large {\displaystyle S_{m}(n) = {\frac {1}{m + 1}}\sum_{k = 0}^{m}{\binom {m + 1}{k}} B_{k}^{+} n^{m + 1 - k } = m! \sum_{k = 0}^{m}{\frac {B_{k}^{+}n^{m + 1 - k}}{k! ( m + 1 - k )!}}}$$
توجه داشته باشید که در اینجا ضرایب دو جملهای را به صورت $$\binom{m+1}{ k}$$ نشان دادهایم.
برای مثال $$m$$ را برابر با ۱ گرفته و مجموع اعداد مثلثی (Triangular Numbers) مانند $$0,1,3,6, \ldots$$ را محاسبه میکنیم.
$$\large {\displaystyle 1 + 2 + \cdots + n = {\frac {1}{2}}(B_{0}n^{2}+2B_{1}^{+}n^{1}) = {\tfrac {1}{2}}(n^{2} + n)}$$
همچنین اگر $$m=2$$ باشد، مجموع «اعداد هرمی مربع» (Square Pyramidal Numbers) به شکل $$ 0 ,1,5 ,14 , \ldots$$ را به صورت زیر بدست میآوریم.
$$\large {\displaystyle 1^{2} + 2^{2} + \cdots + n^{2} = {\frac {1}{3}}(B_{0}n^{3} + 3B_{1}^{+}n^{2} + 3 B_{2}n^{1}) }$$
$$ \large {\displaystyle = {\frac {1}{3}} \left(n^{3} + {\tfrac {3}{2}}n^{2} + {\tfrac {1}{2}} n \right)} $$
سری تیلور و اعداد برنولی
اعداد برنولی در سری تیلور برای بسط توابع مثلثاتی نیز ظاهر میشوند. در ادامه بسط تیلور تانژانت، کتانژانت، تانژانت هایپربولیک و کتانژانت هایپربولیک را مشاهده میکنید.
تانژانت
بسط تیلور تابع تانژانت به کمک اعداد برنولی در رابطه زیر دیده میشود. مشخص است که دامنه تغییرات $$x$$ در حدود $$(-\pi/2,\pi/2)$$ تغییر میکند.
$$ \large {\displaystyle {\begin{aligned}\tan x&=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}}{(2n)!}}\;x^{2n-1},&\left|x\right|&<{\frac {\pi }{2}}\\\end{aligned}}} $$
کتانژانت
به همین ترتیب بسط تیلور تابع کتانژانت را با اعداد برنولی در ادامه میبینید. دامنه تغییرات $$|x|$$ در بازه $$(0,\pi)$$ است.
$$ \large {\displaystyle {\begin{aligned}\cot x&{}={\frac {1}{x}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}B_{2n}(2x)^{2n}}{(2n)!}},&\qquad 0<|x|<\pi \end{aligned}}} $$
تانژانت هایپربولیک
بسط تیلور تابع تانژانت هایپربولیک به کمک اعداد برنولی در رابطه زیر دیده میشود. حدود تغییرات $$|x|$$ نیز در بازه $$[0,\pi/2)$$ است.
$$ \large {\displaystyle {\begin{aligned}\tanh x&=\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}}{(2n)!}}\;x^{2n-1},&|x|&<{\frac {\pi }{2}}\end{aligned}}} $$
کتانژانت هایپربولیک
در سری تیلور تابع کتانژانت هایپربولیک نقش اعداد برنولی در رابطه زیر مشخص شده است. کرانهای $$|x|$$ نیز بازه $$(0, \pi)$$ است.
$$ \large {\displaystyle {\begin{aligned}\coth x&{}={\frac {1}{x}}\sum _{n=0}^{\infty }{\frac {B_{2n}(2x)^{2n}}{(2n)!}},&\qquad \qquad 0<|x|<\pi \end{aligned}}} $$
اعداد برنولی و مثلث خیام-پاسکال
فرض کنید $$A_n$$، ماتریسی باشد که از «اعداد مثلث خیام-پاسکال» (Pascal Triangle Numbers) تشکیل شدهاند که دارای $$n$$ سطر یا ستون است. بین اعداد موجود در مثلث خیام-پاسکال و اعداد برنولی میتوان رابطه زیر را در نظر گرفت.
$$ \large {\displaystyle B_{n}^{+} = {\frac {|A_{n}|}{(n + 1 )!}}}$$
در این بین $$|A_n|$$ دترمینان ماتریس $$A_n$$ بوده و عناصر این ماتریس نیز به صورت زیر هستند.
$$ \large {\displaystyle a_{i,k} = {\begin{cases} 0 & {\text{if }}k > 1 + i \\ { i + 1 \choose k - 1 } & { \text{otherwise}} \end{cases}}} $$
نکته: منظور از $$ { i \choose k }$$ تعداد ترکیبهای $$k$$ از $$i$$ است.
برای مثال مثلث خیام-پاسکال را با ۶ سطر در نظر بگیرید.
$$ \large A_6 = {\begin{pmatrix}1 & 2 & 0 & 0 & 0 & 0 \\ 1 & 3 & 3 & 0 & 0 & 0 \\ 1 & 4 & 6 & 4 & 0 & 0 \\ 1 & 5 & 1 0 & 1 0 & 5 & 0 \\ 1 & 6 & 1 5 & 2 0 & 1 5 & 6 \\ 1 & 7 & 2 1 & 3 5 & 3 5 & 2 1 \end{pmatrix}}$$
آنگاه میتوانیم ششمین عدد برنولی را برحسب دترمینان این ماتریس و به صورت زیر بنویسیم.
$$ \large{\displaystyle B_{6}^{+} = {\frac {\det {\begin{pmatrix} 1 & 2 & 0 & 0 & 0 & 0 \\ 1 & 3 & 3 & 0 & 0 & 0 \\ 1 & 4 & 6 & 4 & 0 & 0 \\ 1 & 5 & 1 0 & 1 0 & 5 & 0 \\ 1 & 6 & 1 5 & 2 0 & 1 5 & 6 \\ 1 & 7 & 2 1 & 3 5 & 3 5 & 2 1 \end{pmatrix}}}{7!}} = {\frac {120}{5040}} = {\frac {1}{42}}}$$
نمایش اعداد برنولی بوسیله انتگرال
انتگرال مختلط زیر را در نظر بگیرید.
$$ \large {\displaystyle b(s) = 2 e^{si \pi /2} \int _{0}^{\infty }{\frac {st^{s}}{1 - e^{2 \pi t}}}{\frac {dt}{t}}}$$
مقدار این انتگرال برای اعداد صحیح زوج ($$2n$$) میتواند اعداد برنولی $$B_{2n}$$ را ایجاد کند.
$$ \large b(2n) = B_{2n} , \;\; n>0$$
برای مثال، اگر $$\zeta$$ تابع زتای ریمان باشد و $$i$$ نیز همان مقدار واحد در اعداد مختلط ($$i^2 = -1$$) در نظر گرفته شود، آنگاه خواهیم داشت:
$$ \large b(3) = \frac{3}{2} \zeta(3)\pi^{-3} i$$
و همچنین
$$ \large b(5) = \frac{-15}{2} \zeta(5)\pi^{-5} i $$
اویلر اعداد یاد شده را در نظر گرفت و محاسبات را به صورت زیر انجام داد.
$$ \large{\displaystyle {\begin{aligned} p & = {\frac {3}{2 \pi ^{3}}}\left( 1 + {\frac {1}{2^{3}}} + {\frac {1}{3^{3}}} + \cdots \right) = 0.0581522 \ldots \\ \large q & = {\frac {15}{2 \pi ^{5}}}\left( 1 + {\frac {1}{2^{5}}} + {\frac {1}{3^{5}}} + \cdots \right) = 0.0254132 \ldots \end{aligned}} } $$
خلاصه و جمعبندی
اعداد برنولی در ریاضیات و دیگر شاخههای مهندسی، از اهمیت زیادی برخوردارند. سری تیلور، توابع مثلثاتی، تابع «دیگاما» (Digamma) و «تریگاما» (Trigamma)، همگی از اعداد برنولی بهره میبرند. ایده اصلی برای پیدا کردن چنین اعدادی، محاسبه مجموع توانهای اعداد صحیح بود. برنولی این مجموع را برای $$n=10$$ محاسبه کرد و اویلر برای $$n=30$$ چنین محاسباتی را صورت داد. در سال ۲۰۰۸، «اولکساندر پاولیک» (Oleksandr Pavlyk) با نرمافزار «متمتیکا» (Mathematica)، مقدار $$B_n$$ را برای $$n$$ برابر با ده میلیون، بدست آورد. این عدد تقریبا دارای ۶۷۶ میلیون رقم است.











مطالب خیلی خوب و مفهومی بودش،ممنونم از شما❤
سپاس فراوان بابت مطالب مفید ارایه شده
دوست گرامی بدنبال مطالعه کلیه روش هاس ارایه شده برای بدست آوردن اعداد برنولی هستم.
آیا منبعی است که بتوان از آنجا به مقصود رسید؟
جستجو در اینترنت؛ جوابگو نمی باشد.