ضرب رادیکال — به زبان ساده

در بیشتر مواقع زمانی که با قضیه فیثاغورس در هندسه یا حل معادله درجه ۲ یا با درجه‌های زوج مواجه هستیم، باید از رادیکال استفاده کنیم. رادیکال در حقیقت عملی است که برعکس توان رسانی انجام می‌شود. اگر اعداد بزرگتر از ۱ باشند، ریشه یا رادیکال آن‌ها، کوچکتر شده و اگر بین ۱ تا ۰ باشند، ریشه آن‌ها بزرگتر از خودشان است. در این نوشتار از مجله فرادرس به بررسی ضرب رادیکال خواهیم پرداخت و با ذکر مثال‌هایی مفاهیم مربوط به رابطه ضرب رادیکال و تبدیل آن به رادیکال ضرب را بازگو خواهیم کرد. همچنین برای کلیت بخشی به مباحث گفته شده، رادیکال با فرجه‌های مختلف را مورد بررسی قرار می‌دهیم. در این بین برای آنکه به یک قاعده کلی برسیم، معمولا عبارت‌های رادیکالی را به صورت توان‌دار نوشته و ضرب را به کار خواهیم برد.

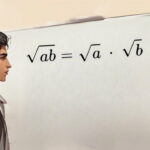
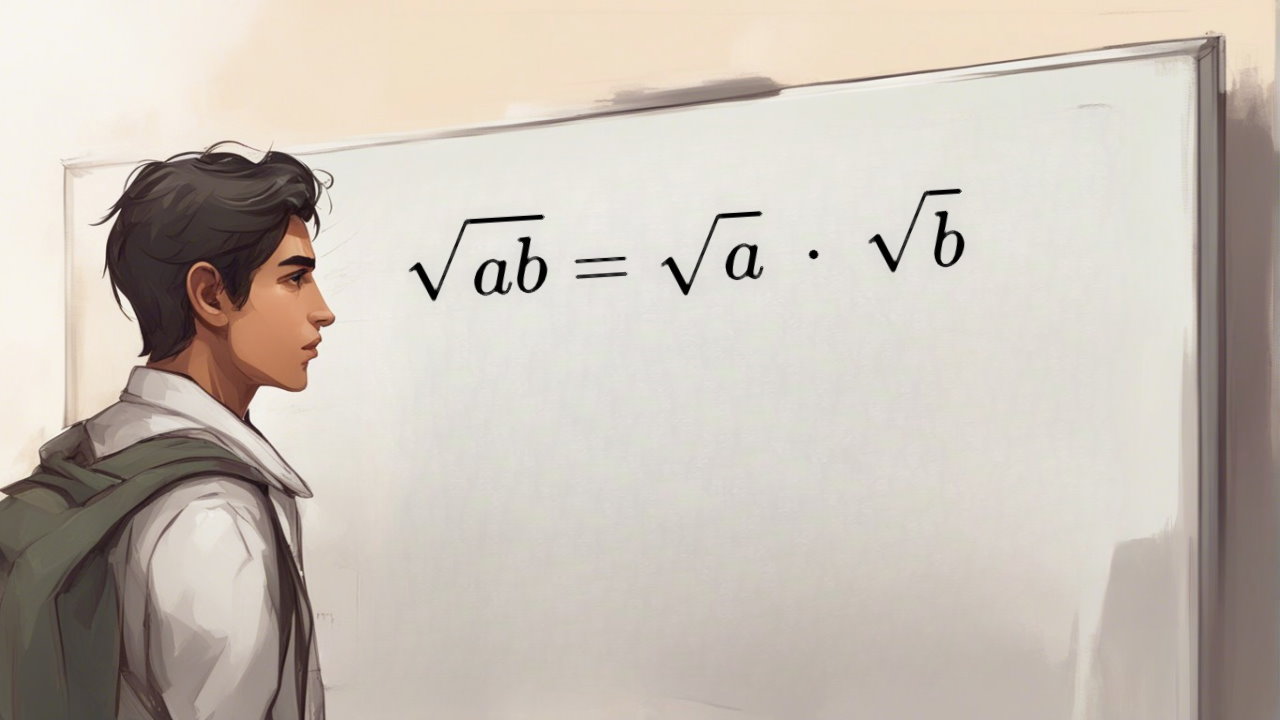
برای آشنایی بیشتر با نحوه محاسبه رادیکال اعداد نوشتار اعداد رادیکالی و محاسبات مربوط به آن ها — به زبان ساده از مجله فرادرس را بخوانید. همچنین نوشتارهای جذر یا محاسبه ریشه دوم عدد — به زبان ساده یا معادله رادیکالی — به زبان ساده نیز خالی از لطف نیست.

ضرب رادیکال

در نوشتارهای دیگر مجله فرادرس با مفهوم رادیکال یا ریشه اعداد آشنا شده‌اید. در اینجا قصد داریم با ضرب رادیکال آشنا شده و جمله‌های جبری که به صورت رادیکالی با یکدیگر رابطه دارند را مورد بررسی قرار دهیم. البته برای یادآوری، به مفهوم رادیکال و ارتباط آن با عبارت‌های توانی اشاره خواهیم کرد.

همانطور که می‌دانید، اگر $$x$$ مقداری باشد که توان یا مربع آن برابر با $$y$$ باشد، آنگاه می‌توانیم برای پیدا کردن $$x$$ از $$y$$ ریشه یا رادیکال بگیریم. این موضوع در رابطه زیر نشان داده شده.

$$\large x^2 = y \rightarrow \sqrt{y} = x$$

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

البته این موضوع را برای توان‌های دیگری از $$x$$ نیز می‌توان به کار برد و مفهوم رادیکال را تعمیم داد. به این ترتیب اگر $$y$$ به صورت توان $$n$$ام از $$x$$ نوشته شده باشد، آنگاه ریشه $$n$$ام $$y$$ برابر است با $$x$$. به بیان ریاضی این گزاره به صورت زیر نمایش داده می‌شود.

$$\large x^n = y \rightarrow \sqrt[n]{y} = x$$

نکته: دلیلی ندارد که مقدار $$n$$ را از میان اعداد طبیعی یا صحیح انتخاب کنیم. مقدارهای مربوط به مجموعه اعداد حقیقی (بدون در نظر گرفتن صفر) می‌تواند مقدار مناسب برای $$n$$ باشد.

از نظر تکنیکی می‌توان ریشه یا رادیکال یک عدد را به صورت یک عبارت توانی نیز نشان داد. برای مثال ریشه دوم یک عدد مثل $$a$$، قابل نمایش به صورت زیر است.

$$\large \sqrt{a} = a^{1/2}$$

همانطور که مشاهده می‌کنید، ریشه دوم به صورت توان ۱/۲ نشان داده شده. همین کار را برای ریشه $$n$$ام نیز می‌توانیم به کار ببریم. به رابطه زیر دقت کنید.

$$\large \sqrt[n]{a} = a^{1/n}$$

رابطه ۱

به باد دارید که عدد نوشته شده در بالای رادیکال، نشانگر مرتبه رادیکالی گیری است. بنا به قرارداد اگر ریشه دوم مورد نظر باشد، مقدار ۲ در بالای رادیکال نوشته نمی‌شود ولی برای مقادیر دیگر حتما باید فرجه رادیکال قید شده باشد.

در نظر گرفتن عبارت‌های رادیکالی به صورت نمایی، این قدرت را به ما می‌دهد که بتوانیم کلیه محاسباتی که برای عبارت‌های توانی به کار می‌بریم، برای عبارت‌های رادیکالی نیز مورد استفاده قرار دهیم. البته باید به یاد داشته باشید که در عبارت‌های رادیکالی با فرجه زوج باید همیشه مقدار زیر رادیکال مثبت باشد، ریشه‌های زوج برای مقادیر منفی تعریف نشده است. زیرا از ضرب دو عدد یکسان، هرگز عدد منفی بوجود نمی‌آید.

نکته: موضوع گفته شده برای ریشه‌های زوج و مقدار مثبت زیر رادیکال، در مجموعه اعداد حقیقی صحت دارد. ولی زمانی که مجموعه مقادیر را گسترش داده و با مجموعه اعداد مختلط سروکار داشته باشیم، مقدار زیر رادیکال برای فرجه‌های زوج می‌تواند منفی نیز باشند.

در ادامه با توجه به قواعدی که برای ضرب رادیکال و یا عبارت‌های توانی به کار خواهیم برد، عبارت‌های رادیکالی را در یکدیگر ضرب کرده یا ضرب رادیکال‌ها را به صورت یک رادیکال در خواهیم آورد. این موضوع در هنگام ساده‌سازی چنین جملاتی اهمیت دارد.

ضرب رادیکال ها با فرجه های برابر

فرض کنید که دو عبارت رادیکالی، به صورت $$\sqrt{x}$$ و $$\sqrt{y}$$ داشته باشیم. واضح است که هر دو رادیکال دارای فرجه (فرجه ۲) یکسان هستند. به این ترتیب حاصل‌ضرب به صورت زیر خواهد بود.

$$\large \sqrt{x} \sqrt{y} = \sqrt{x \cdot y}$$

رابطه ۲

برای مثال در نظر بگیرد که باید $$\sqrt{2}$$ را در $$\sqrt{3}$$ ضرب کنیم. به این ترتیب طبق رابطه بالا خواهیم داشت.

$$\large \sqrt{2} \sqrt{3} = \sqrt{2 \cdot 3} = \sqrt{6}$$

از طرفی برای ساده‌سازی می‌توان عمل عکس را به صورتی انجام داد که رادیکال ضرب را به صورت تفکیکی با ضرب دو رادیکال نوشت. به مثال زیر در این زمینه توجه کنید.

$$\large \sqrt{144} = \sqrt{ 9 \times 16} = \sqrt{9 } \times \sqrt{16} = 3 \times 4 = 12$$

همانطور که می‌بینید، ۱۴۴ را به صورت ضرب دو عامل مربعی درآورده‌ایم. هم ۹ و هم ۱۶ مربع کامل هستند. بنابراین با توجه به عمل عکس رابطه 2، مقدار $$\sqrt{144}$$ را بدست آوردیم. به عنوان یک مثال دیگر به رابطه‌ای تمرکز می‌کنیم که در آن فرجه رادیکال‌ها مقداری برابر ولی غیر از ۲ است.

دو رادیکال $$\sqrt[3]{4}$$ و $$\sqrt[3]{2}$$ را در نظر بگیرید. از آنجا که هر دو فرجه برابر با ۳ هستند، باز هم می‌توانیم هر دو رادیکال را مطابق با رابطه 2 در هم ضرب کنیم.

$$\large \sqrt[3]{4} \times \sqrt[3]{2} = \sqrt[3]{4 \times 2} = \sqrt[3]{8} = 2$$

به طوری کلی قاعده‌ای که در رابطه 2 معرفی شد را برای رادیکال با فرجه $$n$$ به شکل زیر خواهیم نوشت.

$$\large \sqrt[n]{x} \sqrt[n]{y} = \sqrt[n]{x \cdot y}$$

رابطه ۳

توجه داشته باشید که در رابطه ۳، علامت $$\cdot$$ به معنی ضرب دو عبارت زیر رادیکال است. مشخص است که از رابطه ۳ می‌توان در دو جهت استفاده کرد. از یک طرف، تساوی را از راست به چپ نتیجه گرفت و از طرف دیگر معادله را از چپ به راست به کار برد. معمولا زمانی که لازم است عبارت زیر رادیکال را ساده کنیم، از چپ به راست، رابطه 3 را به کار می‌بریم.

ضرب رادیکال ها با فرجه های متفاوت

در قسمت قبل به مثال‌هایی پرداختیم که فرجه هر دو رادیکال یکسان بودند. در این بخش به حالتی می‌پردازیم که فرجه‌های دو رادیکال با هم تفاوت دارند. در این صورت بهتر است رادیکال‌ها را به صورت عبارت‌های توانی نوشت و براساس آن اقدام کرد.

فرض کنید که قرار است دو رادیکال $$\sqrt[3]{2}$$ را در $$\sqrt[4]{2}$$ ضرب کنیم. ابتدا آن‌ها به صورت توان‌دار نوشته، سپس عمل ضرب را انجام می‌دهیم.

$$\large \sqrt[3]{2} \times \sqrt[4]{3} = 2^{1/3} \times 2^{1/4} = 2^{1/3 + 1/4} = 2^{7/12} = \sqrt[12\;]{2^7}$$

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

همانطور که می‌بینید در گام آخر، دوباره عبارت نمایی را به صورت رادیکالی درآورده‌ایم. مشخص است که این کار زمانی امکان‌پذیر است که مقادیر زیر رادیکال یکسان باشند. در نتیجه، ضرب دو رادیکال فقط در دو حالت قابل اجرا و ساده‌ شدن است.

• اگر فرجه رادیکال‌ها در ضرب، یکسان باشد از رابطه ۳ کمک خواهیم گرفت.
• اگر مقدار زیر رادیکال‌ها در ضرب، یکسان باشند از رابطه ۴ استفاده خواهیم کرد.

$$\large \sqrt[n ]{x} \times \sqrt[m ]{x} = x^{( 1/n )+( 1/m)} = x^{\frac{ m +n }{ n \times m }} = \sqrt[ n \times m\;\;]{x^{( n +m)}}$$

رابطه ۴

برای مثال ضرب دو رادیکال زیر را در نظر بگیرید.

$$\large \sqrt[ 3 ]{ 5} \times \sqrt[ 4 ]{ 5} = \sqrt[3 \times 4\; ]{5^{ 3 + 4}} =\sqrt[12\;]{ 5^ 7}$$

از این کار برای ساده‌سازی عبارت‌های جبری نیز می‌توان استفاده کرد.

$$\large \sqrt[ 3]{ x} \times \sqrt[4]{x} = \sqrt[12\; ]{x^{3+4}} =\sqrt[12\;]{ x^7}$$

واضح است که به علت یکسان بودن جملات زیر رادیکال، این عمل امکان‌پذیر خواهد بود.

تقسیم رادیکال

برای تقسیم دو عدد رادیکالی نیز درست به مانند ضرب عمل می‌کنیم با این تفاوت که برای نشان دادن تقسیم، مقسوم علیه را به صورت معکوس و به شکل مضرب در محاسبات منظور می‌کنیم یا به مانند رابطه ضرب رادیکال‌ها، تقسیم را هم به همان شکل به کار می‌بریم. البته در این بین تمام شرایط و قواعدی که برای ضرب عبارت‌های رادیکالی گفتیم، باید لحاظ شود.

برای مثال فرض کنید که قرار است $$\sqrt{x}$$ را به $$\sqrt{y}$$ تقسیم کنیم. در این حالت به علت اینکه فرجه هر دو رادیکال یکسان است (فرجه‌ها ۲ هستند)، از قاعده تبدیل تقسیم دو عبارت رادیکالی به رادیکال تقسیم استفاده کرده و رابطه تقسیم را به صورت زیر می‌نویسیم.

$$\large \dfrac{\sqrt{ x}}{ \sqrt{ y}} = \sqrt{ \dfrac{x }{ y}}$$

برای مثال، رابطه زیر را در نظر بگیرید.

$$\large \dfrac{\sqrt{ 15}}{ \sqrt{ 3}} = \sqrt{ \dfrac{15 }{ 3}} =\sqrt{ 5}$$

فیلم مجموعه آموزش دروس متوسطه دوم و کنکور – درس، تمرین، حل مثال و تست در فرادرس

کلیک کنید

این بار فرجه‌ها را نامساوی در نظر می‌گیریم.

$$\large \dfrac{ \sqrt[ n]{ x}}{ \sqrt[ m]{ x}} = \dfrac{ x^{ 1/n}}{ x^{ 1/m}} = x^{ 1/n-1/m}$$

به عنوان یک مثال به رابطه زیر توجه کنید.

$$\large \dfrac{\sqrt[3\;]{ 15}}{ \sqrt[4\;]{ 15}} = \sqrt[12\;]{ 15}$$

در مثال بعد، از آنجا که توان ۱۵ در زیر رادیکال یک واحد بیشتر از فرجه رادیکال است، $$15^3$$ از داخل رادیکال با فرجه ۳، خارج شده و به شکل ۱۵ درآمده است تا عبارت مربوطه، خواناتر و ساده‌تر باشد.

$$\large \sqrt[3\;]{15^4} = \sqrt[3\;]{15^3 \times 15} = 15 \sqrt[3\;]{15}$$

خلاصه و جمع‌بندی

همانطور که در این مطلب از مجله فرادرسخواندید، جذرگیری یا محاسبه ریشه برای ضرب دو عبارت قابل تبدیل به ضرب ریشه‌ها یا رادیکال‌ها است. البته وجود فرجه یکسان برای رادیکال‌ها از شرط‌های اولیه برای امکان ضرب این گونه جمله‌ها است. از آنجایی که رادیکال‌ گیری، عکس عمل توان رساندن در نظر گرفته می‌شود، به راحتی قواعد توان و ضرب جمله‌های توان‌دار برای محاسبه ضرب رادیکال قابل استفاده است. به همین جهت، می‌توان همان عملیاتی که برای توان رساندن (مثل ضرب) انجام می‌دهیم را برای جذر یا رادیکال (مثل تقسیم) تکرار می‌کنیم. همانطور که در این مطلب از مجله فرادرس خواندید، مثال‌های مختلفی از تبدیل ضرب رادیکال‌ها به رادیکال ضرب و برعکس مطرح شد تا فراگیران به خوبی با این موضوع آشنا شده و به راحتی آن را به کار گیرند.