سلول واحد در بلورشناسی چیست؟ – به زبان ساده

سلول واحد کوچک‌ترین بخش سازنده یک بلور است که در سرتاسر آن تکرار می‌شود. این واحد سازنده انواع مختلفی دارد که با توجه به ویژگی‌‌های خود، ساختار بلور را پدید می‌آورند. به همین دلیل آشنایی با این مفهوم دروازه ورود به دنیای ترکیبات شیمیایی جامد بلوری در شیمی کریستالوگرافی است. آشنایی با این مفهوم برای دانشجویان رشته‌های شیمی، مهندسی مواد و رشته‌های مرتبط از اهمیت به‌سزایی برخوردار است و به آن‌ها در فراگیری مفاهیم مرتبط پیشرفته کمک می‌کند.

در این مطلب مجله فرادرس ابتدا به بررسی این مفهوم در ساختار بلوری می‌پردازیم و سپس انواع آن را بررسی می‌کنیم. توجه داشته باشید که این واحد سازنده بسیار متنوع است و در اینجا به برخی از متداول‌ترین آن‌ها پرداخته‌ایم.

یکی از مهم‌ترین ویژگی‌ها در مورد هر سلول واحد، فاکتور فشردگی آن است که پایداری آن را مشخص می‌کند که این مورد را برای تعدادی از رایج‌ترین آن‌ها محاسبه می‌کنیم. در ادامه عدد کوئوردیناسیونی که هر سلول به خود می‌گیرد و تصویر آن‌ها را مرور می‌کنیم. در نهایت نیز برای عمق بخشیدن به درک خود از این مفهوم تعداد مثال را به همراه پاسخ تشریحی و چند تمرین تستی بررسی خواهیم کرد.

سلول واحد چیست؟

«سلول واحد» (Unit Cell) کوچک‌ترین بخش یک شبکه بلوری است که به‌صورت واحدهای تکرارشوند در سراسر آن مشاهده می‌شود. در واقع می‌توان این‌طور بیان کرد که این سلول‌های واحد هستند که در جهت‌های مختلف تکرار می‌شوند و شبکه بلور را به وجود می‌آورند.

در تصویر زیر می‌توانید رابطه بین این ساختار و شبکه بلوری را به‌صورت بسیار واضح مشاهده کنید.

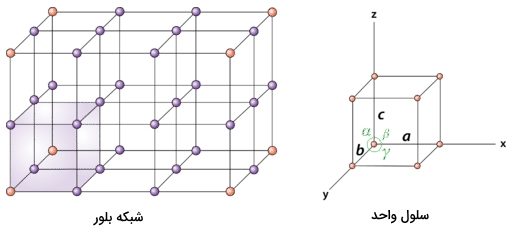
در سلول واحد جهت‌گیری $$a$$ و $$b$$ و $$c$$ تفاوتی با یکدیگر ندارند زیرا اندازه طول و عرض و ارتفاع در آن با یکدیگر برابر است. به‌طور کلی می‌توان برای سادگی درک، جهت‌گیری و مختصات نقاط را در سلول واحد به‌‌صورت زیر نمایش داد. همان‌طور که مشاهده می‌کنید بردار $$a$$ در جهت بالا، بردار $$b$$ حرکت در جلوی مکعب و بردار $$c$$ حرکت به پشت مکعب را نشان می‌دهد.

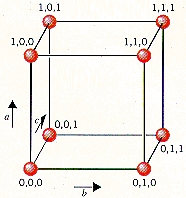
همچنین به نقطه شبکه که در سمت چپ و پایین قرار دارد، مختصات (۰،۰،۰) را نسبت می‌دهیم. در صورتی که در طول بردار $$a$$ به اندازه یک طول پیش برویم، به نقطه شبکه‌ای با مختصات (۱،۰،۰) خواهیم رسید. همچنین مختصات (۰،۰،۱) و (۰،۱،۰) به ترتیب به‌‌صورتی به دست می‌آید که به اندازه یک طول در جهت بردار $$b$$ و $$c$$ پیشروی کنیم. از این مختصات می‌توان برای پی بردن به مکان هر اتم در شبکه استفاده کرد.

در صورتی که با ساختار سلول واحد آشنایی داشته باشیم، می‌توانیم با در دست داشتن اطلاعات محدودی، بلور ترکیبات متفاوت را شناسایی کنیم. برای مثال به ویژگی‌های ساختار سزیم کلرید در ادامه توجه کنید.

• سزیم کلرید در سلول واحد مکعبی تشکیل بلور می‌دهد.
• طول لبه سلول واحد آن برابر با ۰٫۴۱۲۳ نانومتر است.
• در مختصات (۰،۰،۰) یک آنیون $$Cl^-$$ حضور دارد.
• در مختصات (۱٫۲،۱٫۲،۱٫۲) یک کاتیون $$Cs^+$$ حضور دارد.

از آن‌جا که لبه‌های سلول باید دارای نقاط شبکه یکسان باشند، وجود یون کلرید در مختصات (۰،۰،۰) نشان‌دهنده است است که در تمامی گوشه‌های این سلول، همین یون حضور دارد. همچنین مختصات سزیم آن را در مرکز مکعب سلول قرار می‌دهد. از آن‌جا که در مرکز سلول، تنها یک نقطه با این مختصات حضور دارد، تنها یک یون سزیم نیز در ساختار داریم.

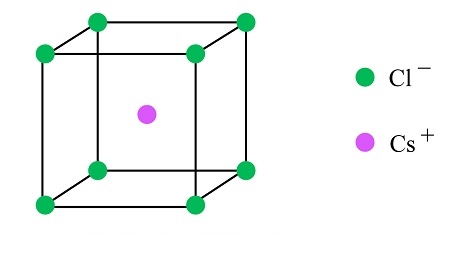
بنابراین سلول واحد سزیم کلرید دارای ۸ عنصر کلر در گوشه‌ها و یک سزیم در مرکز است که به نام سلول واحد مکعبی مرکز پر شناخته می‌شود. در بخش بعد می‌خواهیم با انواع سلول‌های واحد موجود آشنا شویم. در تصویر بالا ساختار سلول مربوط به بلور سزیم کلرید را مشاهده می‌کنید.

انواع سلول واحد

سلول‌های واحد با توجه به ساختار خود انواع مختلفی دارند که در ادامه به آن‌ها خواهیم پرداخت.

• سلول واحد مکعبی ساده
• سلول واحد مکعبی مرکز پر
• سلول واحد مکعبی وجوه پر
• سلول واحد شش‌ضلعی فشرده

سلول واحد مکعبی ساده

در حالتی که نقاط شبکه تنها در گوشه‌های یک ساختار وجود داشته باشند، آن را به نام «سلول واحد مکعبی ساده» (Simple Cubic Unit Cells) می‌شناسیم که نمونه‌ای از آن را در تصویر زیر مشاهده می‌کنید. این سلول را به اختصار با $$SC$$ نمایش می‌دهند. در واقع نقاطی که در ساختار مشخص شده‌اند، جایگاه قرارگیری فلز، یون یا مولکول‌های سازنده ساختار بلوری هستند و در این نوع سلول به دلیل قرارگیری در گوشه‌های مکعب، یافتن جایگاه آن‌ها در بلور آسان است.

این نوع سلول به دلیل داشتن «فشردگی چگالی» (Packing of Density) پایین به ندرت در ساختار بلورها مشاهده می‌شود. از آنجا که کناره‌‌های سلول واحد دارای فواصل برابری هستند، تمامی آن‌ها ساختاری مشابه با یکدیگر دارند. همچنین ذراتی که در این ۸ نقطه قرار دارند باید از یک نوع و کاملا مشابه یکدیگر باشند. البته ذرات دیگری نیز می‌توانند در وجوه یا مرکز این سلول واحد حضور داشته باشند و ساختارهای جدیدی را پدید بیاورند که در ادامه به معرفی آن‌ها نیز می‌پردازیم.

بنابراین برای اینکه ساختاری را سلول واحد مکعبی ساده بدانیم باید دارای ۸ ذره برابر در ۸ گوشه یک مکعب باشد.توجه داشته باشید که وجود ۸ ذره در این ساختار به این معنا نیست که دارای ۸ اتم است. برای به دست آوردن تعداد اتم‌های هر ساختار راهکار دیگری وجود دارد که در بخش‌های بعدی به معرفی آن می‌پردازیم. «بازدهی فشردگی» (Packing Efficiency) یا «فاکتور فشردگی» (Packing Factor) در این سلول برابر با ۵۲٪ است. از این نوع سلول واحد می‌توان به بلور پلونیوم اشاره کرد.

سلول واحد مکعبی مرکز پر

«سلول واحد مکعبی مرکز پر» (Body Centered Cubic Unit Cells) که به اختصار با $$BCC$$ نشان داده می‌شود، حالتی است که نقاط شبکه هم در ۸ گوشه‌ مکعب، هم در مرکز آن وجود دارد. در واقع در این سلول واحد ۹ نقطه شبکه وجود دارد که می‌توانید آن‌ها را در تصویر زیر مشاهده کنید.

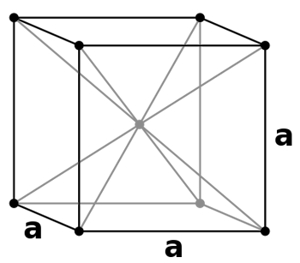
در این سلول نیز ساختار تمامی ذرات با یکدیگر برابر است. این نوع سلول از سلول واحد مکعبی ساده رواج بیشتری دارد زیرا در آن اتم‌ها با یکدیگر در اتصال محکمی قرار دارند. در این مورد مقدار بازدهی فشردگی برابر با ۶۸٪ است که به میزان ۱۶٪ از نوع قبلی بیشتر خواهد بود. از این نوع سلول می‌توان به پتاسیم، کروم و آهن اشاره کرد.

سلول واحد مکعبی وجوه پر

در «سلول واحد مکعبی وجوه پر» (Face Centered Cubic Unit Cells) که آن را به اختصار با $$FCC$$ نمایش می‌دهیم، ذرات علاوه بر گوشه‌های مکعب در مرکز تمامی وجوه نیز حضور دارند. به عبارتی در سرتاسر این ساختار ۱۴ ذره وجود دارد که می‌توانید آن را در تصویر زیر مشاهده کنید.

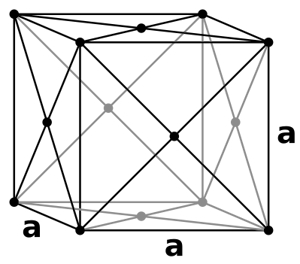
از آن‌جا که فشردگی و استحکام ذره‌های در این ساختار بیشتر از دو ساختار قبلی است، متدوال‌ترین سلول در بلورها به شمار می‌رود. همچنین بازدهی فشردگی آن نیز بیشترین مقدار و برابر با ۷۴٪ است.

سلول واحد شش ضلعی فشرده

یکی دیگر از ساختارهای متداول بلوری در فلزها «سلول واحد شش‌ضلعی فشرده» (Hexagonal Close Packed Unit Cell) است که به اختصار با $$HCP$$ نمایش داده می‌شود. تصویر این ساختار را در زیر مشاهده می‌کنید که به شکل هرم است.

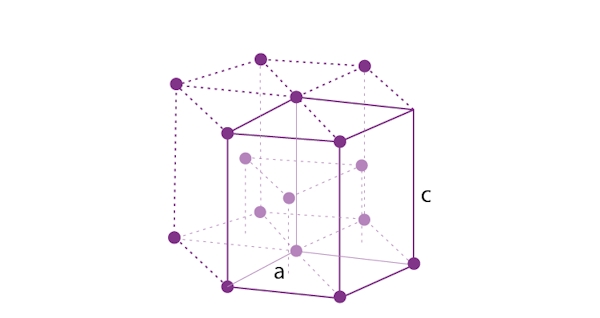
این سلول یکی از پایدارترین ساختارها را دارد و فاکتور فشردگی آن برابر با ۷۴٪ است. تعداد اتم‌های موجود در این سلول برابر با ۶ عدد است. به دلیل پایداری بالا، بلورهای زیادی این ساختار را به خود می‌گیرند که در فهرست زیر به آن‌ها اشاره کرده‌ایم.

• اسکاندیوم
• تیتانیوم
• کبالت
• روی
• زیرکونیوم
• کادمیوم
• لوتتیوم
• هافنیوم
• اوسمیوم
• تالیوم

مثال از سلول واحد

تا اینجا با انواع سلول‌های واحد آشنا شدیم. در این بخش می‌خواهیم ساختار بلوری رایج و متداول را با جزئیات بررسی کنیم.

سلول واحد سدیم کلرید

در سلول سازنده بلور سدیم کلرید، یون‌های سدیم در حفره‌های هشت‌وجهی بین صفحات یون کلرید قرار دارند. نحوه این قرارگیری را در تصویر زیر مشاهده می‌کنید.

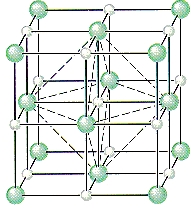
در فهرست زیر به برخی از مهم‌ترین ویژگی‌های این سلول اشاره کرده‌ایم.

• سلول واحد این بلور از نوع مکعبی است.
• طول هر وجه این سلول برابر با ۰٫۵۶۴۱ نانومتر است.
• موقعیت‌‌هایی که توسط یون کلرید اشغال می‌شوند دارای مختصات (۰،۰،۰) و (۱٫۲،۱٫۲،۰) و (۱٫۲،۰،۱٫۲) و (۰،۱٫۲،۱٫۲) هستند.
• موقعیت‌هایی که توسط یون سدیم اشغال می‌شوند نیز دارای چهار مختصات به‌صورت (۱٫۲،۱٫۲،۱٫۲) و (۱٫۲،۰،۰) و (۰،۱٫۲،۰) و (۰،۰،۱٫۲) هستند.

فاصله بین ذرات در سلول واحد

نیکل از جمله فلزات دارای سلول واحد مکعبی است. در این بخش می‌خواهیم چرایی تشکیل این سلول واحد نیکل را مورد بررسی قرار دهیم. پیش از آن یادآور می‌شویم که جرم اتم نیکل برابر با $$9.75\times10^{-23}$$ گرم و شعاع یونی آن نیز برابر با $$1.24\times10^{-10}$$ متر است. یکی از روش‌هایی که می‌توان از آن برای مطالعه ساختار ذرات در مقیاس کوچک استفاده کرد، روش تابش الکترومغناطیسی است.

در سال ۱۹۱۲ میلادی، «ماکس فون لائو» (Max Von Laue) متوجه شد که اشعه ایکس پس از برخورد با سطح بلور، الگوهای انکساری مشابه با الگوهای تولید شده در عبور نور از میان شکافی نازک را از خود تولید می‌کند.

مدتی بعد فیزیکدان انگلیسی «سر ویلیام لارنس برگ» (Sir William Lawrence Bragg) معادله‌ای را پیشنهاد داد که به نام «قانون برگ» (Bragg Equation) شناخته می‌شود. به کمک این معادله می‌توان فاصله بین صفحات اتم‌ها در بلور را از طریق انکسار اشعه ایکس (طول موج)، به دست آورد. معادله این قانون را می‌توان به‌صورت زیر نشان داد.

$$n\lambda = 2d sin T$$

با استفاده از این رابطه، فاصله بین صفحات اتم‌ها در بلور نیکل برابر با ۰٫۳۵۲۴ نانومتر به دست می‌آید، بنابراین طول هر سلول نیز برابر با همین مقدار است. با این حال نمی‌توان بر همین فاصله اکتفا کرد و باید بتوانیم نوع سلول واحد مکعبی آن را نیز به دست بیاوریم. برای این کار باید چگالی فشردگی آن را بیابیم که در ادامه به آن می‌پردازیم. پیش از آن می‌خواهیم نحوه محاسبه تعداد اتم‌های موجود در هر نوع سلول را بررسی کنیم.

تعیین تعداد اتم در سلول واحد

همان‌طور که در تصویر زیر مشاهده می‌کنید، اتم‌هایی که در گوشه، وجه و لبه یک سلول واحد حضور دارند، با سلول‌های واحد کناری خود به اشتراک گذاشته می‌شوند. در صورتی که اتمی در یکی از وجوه حضور داشته باشد بین دو سلول به اشتراک گذاشته می‌شود، بنابراین تنها نیمی از یک اتم به هر کدام از این سلول‌های واحد تعلق دارد.

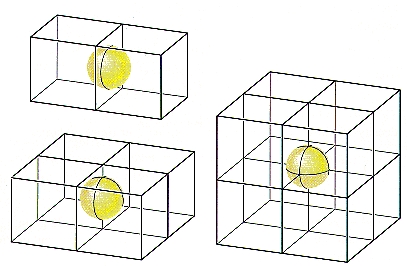
در صورتی که اتمی در یکی از لبه‌ها حضور داشته باشد بین چهار سلول واحد به اشتراک گذاشته می‌شود، بنابراین تنها یک چهارم از یک اتم به هر کدام از این سلول‌های واحد تعلق دارد. مورد آخر زمانی است که یک اتم در گوشه سلول قرار داشته باشد که در این صورت تنها یک هشتم از یک اتم به هر کدام از این سلول‌های واحد تعلق دارد. این نحوه اشتراک گذاری از تصویر بالا قابل استنباط است.

با توجه به این نکات می‌توانیم تعداد اتم‌های موجود در هر سلول را به درستی محاسبه کنیم. برای مثال بلور نیکل را در نظر داشته باشید که در هر گوشه آن یک اتم وجود دارد. با این حال نمی‌توان تعداد اتم‌های موجود در این سلول را برابر با ۸ در نظر گرفت زیرا هر کدام از آن‌ها تنها به میزان یک هشتم در این سلول حضور دارند و در اشتراک با سلول‌های دیگر هستند. در نهایت در این سلول واحد تنها ۱ اتم حضور دارد و می‌توان محاسبات آن را به‌صورت زیر نمایش داد.

$$8 \times\frac{1}{8} = 1 \;atom$$

محاسبات بالا در مورد یک سلول واحد مکعبی ساده صدق می‌کند که در آن، اتم‌ها تنها در گوشه‌ها حضور دارند. در صورتی که محاسبات را برای سلول مکعبی مرکز پر انجام دهیم، نتیجه برابر با ۲ اتم خواهد بود زیرا در این سلول ۱ اتم به‌صورت مجزا در مرکز قرار داد که با سلول‌های دیگر به اشتراک گذاشته نمی‌شود.

$$(8 \times\frac{1}{8} )+1=2 \;atom$$

در نهایت نیز می‌خواهیم این محاسبات را برای سلول واحد مکعبی وجوه پر انجام دهیم. در این سلول ۶ اتم در وجوه قرار دارند که نیمی از آن‌ها به هر سلول تعلق دارد. همچنین ۸ اتم در گوشه‌ها وجود دارند که تنها یک هشتم آن‌ها متعلق به این سلول واحد است. بنابراین در مجموع ۴ اتم نیکل در آن وجود دارد که می‌توان آن را به‌‌صورت زیر نشان داد.

$$(8 \times\frac{1}{8} )+(6\times\frac{1}{2})=4 \;atom$$

همان‌طور که مشاهده می‌کنید تعداد اتم‌های موجود در هر ساختار با دیگری متفاوت است و به همین علت نیز چگالی فشردگی آن‌ها با یکدیگر متفاوت است. در این بین سلول واحد مکعبی وجوه پر بیشترین تعداد اتم و در نتیجه بیشترین چگالی را دارد. در ادامه می‌خواهیم مقدار این چگالی را برای نیکل محاسبه کنیم. برای انجام این کار نیاز به دانستن حجم سلول بر حسب مترمکعب و جرم یک اتم نیکل داریم.

برای به دست آوردن حجم یک سلول واحد، طول هر یک وجه آن را به توان ۳ می‌رسانیم. پیشتر با استفاده از رابطه مربوط، این را به دست آورده‌ایم، بنابراین مقدار آن را در ابطه زیر جایگذاری می‌کنیم تا حجم به دست آید.

$$V=a^3=(0.3524 \mathrm{~nm})^3=0.04376 \mathrm{~nm}^3$$

در ادامه باید واحد حجم را از نانومتر مکعب به سانتی‌متر مکعب تبدیل کنیم. همان‌طور که می‌دانید هر ۱ سانتی‌متر مکعب برابر با $$10^7$$ نانومتر مکعب است، بنابراین تبدیل را به‌صورت زیر انجام می‌دهیم.

$$4.376 \times 10^{-2} \mathrm{~nm}^3 \times\left[\frac{1 \mathrm{~cm}}{10^7 \mathrm{~nm}}\right]^3=4.376 \times 10^{-23} \mathrm{~cm}^3$$

جرم اتم نیکل را می‌توان از وزن اتمی این فلز و عدد آووگادرو به دست آورد که به شکل زیر این کار را انجام می‌دهیم.

$$\frac{58.69 \mathrm{~g} \mathrm{Ni}}{1 \mathrm{~mol}} \times \frac{1 \mathrm{~mol}}{6.022 \times 10^{23} \text { atoms }}=9.746 \times 10^{-23} \text { g/atom }$$

بنابراین در صورتی که نیکل تشکیل بلور با ساختار سلول مکعبی ساده بدهد، چگالی آن برابر با ۲٫۲۳ گرم بر سانتی‌متر مکعب خواهد بود که نحوه محاسبه آن را در زیر مشاهده می‌کنید.

$$\frac{9.746 \times 10^{-23} \mathrm{~g} / \text { unit cell }}{4.376 \times 10^{-23} \mathrm{~cm}^3 / \text { unit cell }}=2.23 \mathrm{~g} / \mathrm{cm}^3$$

از آنجایی که تعداد اتم‌های ساختار سلول مکعبی مرکز پر دو برابر سلول واحد مکعبی ساده است، برای به دست آوردن چگالی آن، عدد ۲ را در صورت کسر وارد می‌کنیم و نتیجه به‌صورت زیر خواهد بود.

$$\frac{2\left(9.746 \times 10^{-23} \mathrm{~g} / \text { unit cell }\right)}{4.376 \times 10^{-23} \mathrm{~cm}^3 / \text { unit cell }}=4.45 \mathrm{~g} / \mathrm{cm}^3$$

در نهایت نیز چگالی نیکل را در صورت داشتن سلول مکعبی وجوه پر به‌صورت زیر محاسبه می‌کنیم.

$$\frac{4\left(9.746 \times 10^{-23} \mathrm{~g} / \text { unit cell }\right)}{4.376 \times 10^{-23} \mathrm{~cm}^3 / \text { unit cell }}=8.91 \mathrm{~g} / \mathrm{cm}^3$$

مقدار چگالی نیکل به‌صورت تجربی برابر با ۸٫۹ گرم بر سانتی‌متر مکعب است و می‌توانیم این‌طور جمع‌بندی کنیم که ساختار بلوری این فلز دارای سلول مکعبی از نوع وجوه پر است. از این روش می‌توان برای حدس در مورد ساختار سازنده ترکیبات مختلف بهره برد.

فاکتور فشردگی و حجم سلول واحد fcc

«فاکتور فشردگی اتمی» (Atomic Packing Factor)، شاخصی است که از آن برای به دست آوردن چگالی سلول استفاده می‌شود. فاکتور فشردگی اتمی را به اختصار با APF نمایش می‌دهند و می‌توان مقدار آن را از رابطه زیر به دست آورد.

$$APF=\frac{V_{atom}}{V_{total}}$$

حجم کل یک سلول واحد برابر با حجم مکعب است. در صورتی که اندازه یکی از وجوه آن برابر با $$a$$ باشد، حجم آن از رابطه زیر قابل محاسبه است.

$$V_{total}=a^3$$

همچنین تعداد کل اتم‌های موجود در سلول واحد مکعبی وجوه پر برابر با ۴ است که پیش از این نحوه محاسبه آن را به‌تفضیل بررسی کردیم. از رابطه زیر می‌توان برای به دست آوردن حجم کره استفاده کرد.

$$\frac{4}{3}\pi r^3$$

پیش از این دیدیم که توان سوم $$a$$ برابر با حجم مکعب است و از آنجایی که $$a=2\sqrt{2r}$$ است، برای به دست آوردن حجم مکعب می‌توان رابطه زیر را نوشت.

$$V_{total}=(2\sqrt{2r} )^3$$

بنابراین می‌توانیم برای به دست آوردن حجم سلول $$Fcc$$ از رابطه زیر کمک بگیریم.

$$APF_{Fcc}=\frac{(\frac{8}{8}+\frac{6}{2})\frac{4}{3}\pi r^3}{(2\sqrt{2r)^3}}=\frac{\pi}{3\sqrt{2}}$$

پاسخ این معادله برابر با ۷۴٪ است که مقدار فاکتور فشردگی سلول واحد مکعبی وجوه پر را نشان می‌دهد.

فاکتور فشردگی و حجم سلول واحد bcc

برای به دست آوردن فاکتور فشردگی و حجم سلول $$hcp$$ مراحل قبل را این بار با تغییراتی جزئی انجام می‌دهیم. حجم کل یک سلول واحد برابر با حجم مکعب است. در صورتی که اندازه یکی از وجوه آن برابر با $$a$$ باشد، رابطه زیر برای آن وجود دارد.

$$s=\frac{4}{\sqrt{3}}r$$

همچنین تعداد کل اتم‌های موجود در این نوع سلول برابر با ۴ است که پیش از این نحوه محاسبه آن را به‌تفضیل بررسی کردیم. از رابطه زیر می‌توان برای به دست آوردن حجم کره استفاده کرد.

$$\frac{4}{3}\pi r^3$$

پیش از این دیدیم که توان سوم $$a$$ برابر با حجم مکعب است و از آنجایی که $$a=2\sqrt{2r}$$ است، برای به دست آوردن حجم مکعب می‌توان رابطه زیر را نوشت.

$$V_{total}=(\frac{4}{\sqrt{3}} r)^3$$

بنابراین می‌توانیم برای به دست آوردن حجم سلول واحد $$bcc$$ از رابطه زیر کمک بگیریم.

$$APF_{bcc}=\frac{(\frac{8}{8}+1)\frac{4}{3}\pi r^3}{(\frac{4}{\sqrt{3}}r)}=\frac{\sqrt{3}\pi}{8}$$

پاسخ این معادله برابر با ۶۸٪ است که مقدار فاکتور فشردگی سلول مکعبی وجوه پر را نشان می‌دهد.

فاکتور فشردگی و حجم سلول واحد $$sc$$

مانند قبل باید ابتدا حجم مکعب را به دست آوریم. در این مورد طول هر وجه برابر با $$a$$ است و می‌توان حجم آن را به‌‌صورت زیر به دست آورد.

$$a^3$$

همچنین می‌دانیم که در این نوع سلول ، تعداد اتم‌های موجود برابر با ۱ است. همچنین حجم کره اتم از رابطه $$\frac{4}{{3}} \pi r^3$$ f به دست می‌آيد. با جایگذاری این دو در رابطه فاکتور فشردگی خواهیم داشت:

$$APF_{bcc}=\frac{(\frac{8}{8})\frac{4}{3}\pi r^3}{8r^3}=\frac{\pi}{6}$$

 در نتیجه مقدار فاکتور فشردگی بلور با سلول واحد مکعبی ساده برابر با ۵۲٪ خواهد بود.

فاکتور فشردگی و حجم سلول $$hcp$$

در این بخش می‌خواهیم به نحوه محاسبه فاکتور فشردگی برای سلول واحد شش‌ضلعی فشرده بپردازیم. برای محاسبه حجم این مورد باید حجم هرمی مثلثی را به دست بیاوریم که حاصل ضرب شش‌ضلعی در ارتفاع مثلث است. همچنین این شش‌ضلعی از ۶ مثلث مشابه تشکیل شده است که ابتدا سطح یکی از آن‌ها را مانند زیر به دست می‌آوریم. انجام این محاسبات پیشرفته و زمان‌گیر است به همین دلیل در اینجا نتایج را گزارش می‌دهیم.

$$V_{hcp}=24\sqrt{2}r^3$$

همچنین مقدار فاکتور فشردگی این ساختار برابر با ۷۴٪ است که از رابطه زیر به دست می‌آید.

$$APF_{hcp}=\frac{(\frac{12}{6}+\frac{2}{2}+\frac{3}{1})\frac{4}{3}\pi r^3}{24\sqrt{2}r^3}=\frac{\pi}{3\sqrt{2}}$$

همان‌طور که مشاهده می‌کنید فاکتور فشردگی برای این سلول با سلول مکعبی وجوه فشرده برابر است و در بیشترین مقدار ممکن خود قرار دارد.

ویژگی‌های شبکه بلوری

حال که با سلول واحد و شبکه بلوری آشنا شدیم، در این بخش به بررسی تعدادی از ویژگی‌های مهم شبکه بلوری می‌پردازیم.

عدد کوئوردیناسیون چیست؟

«عدد کوئوردیناسیون» (Coordination Number) که آن را با $$CN$$ مشخص می‌کنند، نشان‌دهنده تعداد همسایه‌هایی است که هر اتم در اطراف خود دارد. در ادامه می‌خواهیم این مورد را در چند سلول واحد مهم بررسی کنیم.

عدد کوئوردیناسیون در سلول واحد $$bcc$$

این عدد برای سلول واحد مکعبی مرکز پر برابر با ۸ است. این عدد خیلی زیاد نیست اما پایداری دسته‌ای از ترکیبات که دارای این سلول واحد هستند به دلیل نزدیک‌ترین همسایه‌های بعدی و نزدیک‌ترین همسایه‌های بعدی بعدی است که می‌توانید آن‌ها را در تصویر زیر به رنگ قرمز و سبز مشاهده کنید.

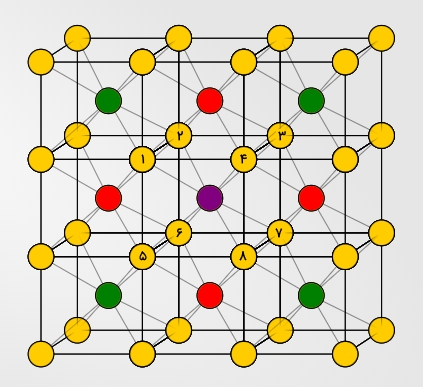
همانطور که مشاهده می‌کنید اتم‌های مجاور اتم بنفش در این تصویر مشخص شده‌اند. در وهله اول ۸ اتم با شماره هستند که اتم‌های همسایه آن به شمار می‌روند. سپس اتم‌های قرمز را داریم که «نزدیک‌ترین همسایه‌های بعدی» (Next Nearest Neighbors) هستند و در نهایت «نزدیک‌ترین همسایه‌های بعدی بعدی» (Next Next Nearest Neighbors) که با رنگ سبز معلوم شده‌اند.

این ساختار یکی از دلایلی است که بلورهایی با سلول واحد مکعبی مرکز پر دارای نقطه ذوب بالاتری هستند. در این ساختار سلول نزدیک‌ترین همسایه‌ها در فاصله $$2r$$ از مرکز و نزدیک‌ترین همسایه بعدی در فاصله $$\frac{4}{\sqrt{3}} r$$ قرار دارد.

عدد کوئوردیناسیون در سلول واحد $$fcc$$

در سلول واحد مکعبی وجوه پر عدد کوئوردیناسیونی برابر با ۱۲ است که در تصویر زیر به رنگ زرد هستند و شماره‌گذاری شده‌اند. از آن‌جا که این عدد برابر با بیشینه مقدار ممکن برای عدد کوئوردیناسیونی است، باعث افزایش پایداری این نوع ساختار می‌شود.

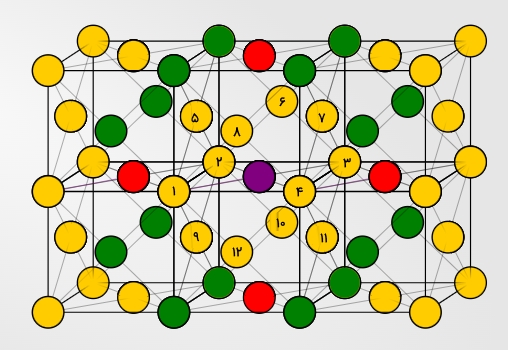
همانطور که مشاهده می‌کنید اتم‌های مجاور اتم بنفش در این تصویر مشخص شده‌اند. در وهله اول ۱۲ اتم با شماره هستند که اتم‌های همسایه آن به شمار می‌روند. سپس اتم‌های قرمز را داریم که نزدیک‌ترین همسایه‌های بعدی هستند و در نهایت نزدیک‌ترین همسایه‌های بعدی بعدی که با رنگ سبز نمایش داده شده‌اند.

عدد کوئوردیناسیون در سلول واحد $$fcc$$

در سلول واحد مکعبی ساده عدد کوئوردیناسیونی برابر با ۶ است که در تصویر زیر به رنگ زرد هستند و شماره‌گذاری نیز شده‌اند. این مقدار نصف عدد کوئوردیناسیون در مورد سلول مکعبی وجوه پر است و همین باعث می‌شود ساختار آن از پایداری زیادی برخوردار نباشد.

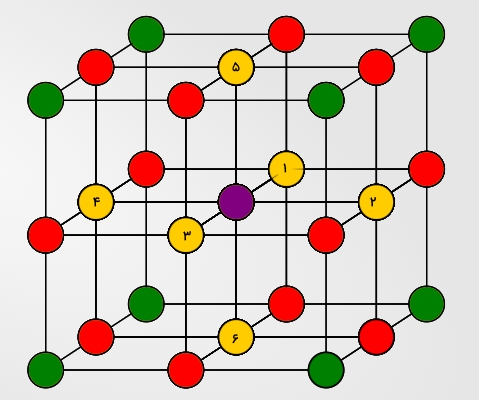
همانطور که مشاهده می‌کنید اتم‌های مجاور اتم بنفش در این تصویر مشخص شده‌اند که ۶ اتم با شماره هستند و اتم‌های همسایه آن به شمار می‌روند. سپس اتم‌های قرمز را داریم که نزدیک‌ترین همسایه‌های بعدی هستند و در نهایت نزدیک‌ترین همسایه‌های بعدی بعدی که با رنگ سبز نمایش داده شده‌اند.

عدد کوئوردیناسیون در سلول $$hcp$$

همان‌طور که در تصویر زیر مشاهده می‌کنید عدد کوئوردیناسیون در سلول واحد $$hcp$$ برابر با ۱۲ است که با رنگ آبی مشخص شده‌اند. این ساختار به دلیل بالا بودن عدد کوئوردیناسیون خود از پایداری بالایی برخوردار است.

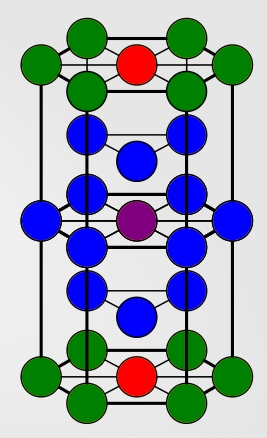
همچنین نزدیک‌ترین همسایه بعدی در این تصویر با رنگ آبی و نزدیک‌ترین همسایه بعدی بعدی با رنگ سبز نمایش داده شده است.

تاریخچه سلول واحد

دانشمندی فرانسوی به نام «آگوست براوه» (Auguste Bravais) مطالعات بسیاری در مورد بلورنگاری انجام داده است. براوه در سال ۱۸۵۰ نشان داد که می‌توان ساختارهای بلوری را به ۱۴ نوع سلول واحد تقسیم کرد که همگی کدام دارای ویژگی‌های زیر هستند.

• سلول واحد ساده‌ترین واحد تکرارشونده ساختارهای بلوری است.
• وجوه مخالف یک سلول با یکدیگر موازی هستند.
• لبه‌های سلول به نقطه‌های مشابهی وصل می‌شوند.

مثال و حل تمرین

حال که می‌دانیم سلول واحد چیست و مفاهیم مرتبط با آن را نیز بررسی کرده‌ایم، می‌خوهیم تعدادی مثال را به همراه پاسخ تشریحی و همچنین تعدادی تمرین چند‌گزینه‌ای مرور کنیم و به دانسته‌های خود از این مفهوم عمق ببخشیم.

مثال

در این بخش تعدادی مثال را به همراه پاسخ تشریحی آن‌ها مرور خواهیم کرد. با توجه به پاسخ‌های تشریحی آن‌ها می‌توانید به سوال‌های مشابه به‌راحتی پاسخ دهید.

مثال اول

ساختار سلول واحد سازنده آلومینیوم از چه نوعی است؟

پاسخ

آلومینیوم دارای سلول واحد مکعبی وجوه پر است که در آن ۴ اتم وجود دارد.

مثال دوم

ساختار بلوری وانادیوم از نوع ... است.

پاسخ

بلور وانادیوم از واحدهای تکرارشونده سلول واحد مکعبی مرکز پر تشکیل شده است که هر کدام از آن شامل ۲ اتم می‌شود.

مثال سوم

تعدادی عنصر را نام ببرید که ساختار سلول واحد آن‌ها از نوعی مرکز پر است.

پاسخ

از جمله بلورهای دارای این ساختار می‌توان به لیتیم، سدیم، پتاسیم، وانادیوم، کروم، آهن، روبیدیم، نیوبیوم، مولیبدن، سزیم، باریم، تانتالوم و تنگستن اشاره کرد.

مثال چهارم

تعدادی عنصر را نام ببرید که ساختار سلول واحد آن‌ها از نوعی وجوه پر است.

پاسخ

از جمله بلورهای دارای این ساختار می‌توان به آلومینیوم، کلسیم، نیکل، مس، استرانسیوم، رودیم، پالادیوم، نقره، ایتربیوم، ایریدیوم، پلاتین، طلا، قلع، اکتینیوم و توریم اشاره کرد.

مثال پنجم

چند مثال از بلور دارای ساختار سلول مکعبی ساده نام ببرید.

پاسخ

در این مورد نمی‌توان مثال‌های زیادی را نام برد زیرا این ساختار دارای عدد کوئوردیناسیون و فاکتور فشردگی پایین است که باعث کاهش پایداری در آن می‌شود. در واقع تنها بلوری که می‌توان به آن اشاره کرد مربوط به پولونیوم رادیواکتیو است. همچنین عنصرهایی مانند فسفر، آنتیموان و تلوریوم در صورتی که شرایط محیا باشند، این ساختار را به خود می‌گیرند.

مثال ششم

در صورتی که شعاع پولونیوم برابر با ۱۶۷ پیکومتر باشد، طول لبه آن را به دست بیاورید.

پاسخ

برای به دست آوردن طول لبه با در دست داشتن شعاع، از رابطه زیر اقدام می‌کنیم. شعاع پولونیوم برابر با ۱۶۷ پیکومتر است و به دلیل داشتن ساختار سلول واحد مکعبی ساده از رابطه زیر به دست می‌آید.

$$2r=2\times167\;pm=334\;pm$$

مثال هفتم

دو نمونه از فلزهایی با سلول مکعبی وجوه پر را مثال بزنید و دلیل خود را برای این پاسخ شرح دهید.

پاسخ

از جمله بلور دارای سلول واحد مکعبی وجوه پر می‌توان به آلومینیوم و قلع اشاره کرد که هر کدام دارای ۴ اتم در یک سلول هستند.

مثال هشتم

سدیم دارای چگالی برابر با ۰٫۹۸۶ گرم بر سانتی‌متر مکعب در طول سلول واحد $$(a)$$ برابر با ۴٫۲۹ آنگستروم است. با توجه به این اطلاعات به سوالا زیر پاسخ دهید.

سوال ۱

در هر ۱ سانتی‌متر مکعب چه تعداد اتم سدیم وجود دارد؟

پاسخ

برای پاسخ به این پرسش ابتدا جرم اتمی میانگین سدیم را به‌صورت زیر محاسبه می‌کنیم.

$$\frac{22.99 \;g.mol^{-1}}{ 6.022 \times 10^{23} \;atoms. mol^{-1}} = 3.82 \times 10^{-23 }\;g/atom$$

سپس تعداد اتم‌های آن را در یک سانتی‌متر مکعب حساب می‌کنیم.

$$\frac{0.968\; g }{3.82 \times 10^{-23} \;g/atom} = 2.54 \times 10^{22}\;atoms. cm^{-3}$$

سوال ۲

در هر سانتی‌متر مکعب چند سلول واحد وجود دارد؟

پاسخ

ابتدا حجم هر سلول واحد را به‌صورت زیر حساب می‌کنیم.

$$(4.29 \times 10^{-8 }\;cm)^3 = 7.89 \times 10^{-23} \;cm^3$$

سپس باید محاسبه کنیم که در هر سانتی‌متر مکعب چه تعداد از آن حضور دارد.

$$\frac{1 \;cm^3}{7.89 x 10^{-23 }\;cm^3 } = 1.27 \times 10^{22 }\;unit \;cells$$

سوال ۳

تعداد اتم‌های موجود در هر سلول واحد را محاسبه کنیم.

پاسخ

برای پاسخ به این سوال به روش زیر عمل می‌کنیم.

$$\frac{2.54\times10^{22}\;atoms}{1.27\times10^{22}\;unit\;cells} = 2 \;atoms/unit \;cells$$

حل تمرین

در این بخش به مرور تعدادی تمرین چند‌گزینه‌ای خواهیم پرداخت.

تمرین اول