خمس در ریاضی چیست؟ – به زبان ساده + مثال های متنوع

خمس، یکی از کسرهای واحد و از معروف‌ترین نسبت‌های ریاضی است. صورت این کسر عدد ۱ و مخرج آن عدد ۵ را نمایش می‌دهد. خمس، با عنوان نسبت یک‌پنجم نیز شناخته می‌شود. برای اینکه خمس یک عدد، شکل یا شی را به دست بیاوریم، آن را به پنج قسمت مساوی تقسیم می‌کنیم. به هر قسمت، خمس می‌گویند. این مفهوم اهمیت و کاربرد زیادی در ریاضی و زندگی روزمره ما دارد. به همین دلیل، در این آموزش از مجله فرادرس، مفهوم خمس در ریاضی را به همراه چندین مثال کاربردی و متنوع مورد بررسی قرار می‌دهیم.

کسر در ریاضی چیست ؟

در ریاضی، به قسمتی از چند قسمت مساوی، کسر می‌گویند. به عنوان مثال، پیتزای نمایش داده شده در تصویر زیر را در نظر بگیرید. این پیتزا را به هشت قسمت مساوی تقسیم کرده‌ایم. بنابراین، هر قسمت، به عنوان کسری از یک پیتزای کامل محسوب می‌شود. به طور دقیق‌تر، هر قسمت، یک‌هشتم پیتزای کامل است.

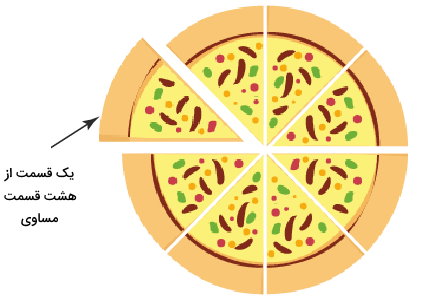
در دنیای ریاضی، روش‌های مختلفی برای نمایش کسرها و اعداد کسری وجود دارد. به عنوان مثال، کسر یک‌هشتم، به صورت زیر نوشته می‌شود:

$$ \frac { ۱ } { ۸ } $$

با برداشتن سه تکه از پیتزا (سه قسمت از هشت قسمت مساوی)، سه-هشتم آن را جدا می‌کنیم.

عدد کسری سه‌هشتم به صورت زیر نمایش داده می‌شود:

$$ \frac { ۳ } { ۸ } $$

به عدد بالای کسر، صورت و به عدد پایین کسر، مخرج می‌گویند. از انواع کسرها می‌توان به موارد زیر اشاره کرد:

• کسر سره یا کسر متعارفی: کسری با صورت کوچک‌تر از مخرج
• کسر ناسره : کسری با صورت بزرگ‌تر از مخرج
• کسر واحد: کسری با صورت ۱
• کسر مختلط: کسری با نمایش ترکیبی از عدد صحیح و کسر متعارفی
• کسر معادل: کسری با صورت و مخرج ضرب شده در یک عدد ثابت یا تقسیم شده بر یک عدد ثابت
• کسر صفر: کسری با صورت ۰

در مثال پیتزا، کسر سه‌هشتم، به عنوان یک کسر متعارفی و کسر یک‌هشتم، به عنوان یک کسر واحد در نظر گرفته می‌شود. برای درک مفهوم خمس، باید با تعریف کسر واحد و نسبت در ریاضی آشنا باشیم.

نسبت در ریاضی چیست ؟

نسبت، یک مفهوم ریاضی است که به منظور مقایسه دو یا چند عدد مورد استفاده قرار می‌گیرد. نسبت‌ها، معمولا با استفاده از کسر نمایش داده می‌شوند. به عنوان مثال، تصویر زیر را در نظر بگیرید. در این تصویر، چهار سیب قرمز و یک سیب سبز وجود دارد.

در تصویر بالا، مجموعا پنج سیب داریم. نسبت سیب‌های قرمز به کل سیب‌ها برابر است با:

$$ \frac { ۴ } { ۵ } $$

نسبت سیب‌های سبز به کل سیب‌ها نیز به صورت زیر نمایش داده می‌شود:

$$ \frac { ۱ } { ۵ } $$

نسبت سیب‌های سبز به سیب‌های قرمز، با دو نسبت قبلی تفاوت دارد. نمایش این نسبت، به صورت زیر است:

$$ ۱ : ۴ $$

نسبت بالا به ما نشان می‌دهد که به ازای هر سیب سبز، چهار سیب قرمز داریم. در مبحث خمس، تمرکز ما بر روی نسبت جز به کل مانند نسبت سیب سبز به کل سیب‌ها (یک‌پنجم) است. از انواع نسبت‌های شناخته شده در ریاضی می‌توان به موارد زیر اشاره کرد:

• نیم یا نصف: یک‌دوم
• ثلث: یک‌سوم
• ربع: یک‌چهارم
• خمس: یک‌پنجم

کاربرد نسبت در زندگی واقعی

کسر و نسب، از پرکاربردترین مفاهیم ریاضی در زندگی روزمره انسان‌ها هستند. اگر تا به حال خوراکی، پول یا هر چیز دیگری را با دیگران تقسیم کرده باشید، به طور مستقیم با مفهوم کسر و نسبت سر و کار داشته‌اید. به عنوان مثال، کودکی را در نظر بگیرید که یک‌دوم خوراکی خود را به دوستش می‌دهد. او در وقع، خوراکی خود را نصف می‌‌کند.

انواع سکه‌های طلا، یکی دیگر از مثال‌های نسبت و کسر در زندگی روزمره هستند. سکه‌های طلا معمولا به انواع تمام سکه، نیم سکه و ربع سکه تقسیم می‌شوند. نیم سکه (یک‌دوم سکه) و ربع سکه (یک‌چهارم سکه)، کسری از یک سکه کامل هستند.

اگر سکه‌ای به اندازه یک‌پنجم تمام سکه وجود داشت، به آن خمس سکه می‌گفتیم. خمس، یکی دیگر از نسبت‌های شناخته شده در ریاضی است. در ادامه، به ارائه تعریف کامل این نسبت و حل چندین تمرین و مثال می‌پردازیم.

تعریف خمس در ریاضی چیست؟

خمس، یکی از نسبت‌های ریاضی و برابر با یک‌پنجم است. هنگام صحبت در مورد خمس یک چیز، آن چیز را به پنج قسمت مساوی تقسیم می‌‌کنیم و یکی از قسمت‌های آن را در نظر می‌گیرم. به عنوان مثال، گل زیر را در نظر بگیرید. این گل، از پنج گلبرگ با شکل و اندازه برابر تشکیل می‌شود. هر گلبرگ، خمس یک گل کامل است.

محاسبه خمس در ریاضی چگونه انجام می شود ؟

خمس در ریاضی، از ضرب یک عدد یا متغیر در کسر واحد یک‌پنجم (عدد $$ \frac { ۱ } { ۵ } $$) به دست می‌آید. فرمول خمس به صورت زیر نوشته می‌شود:

$$ \frac { ۱ } { ۵ } $$ × عدد = خمس عدد

عبارت جبری فرمول خمس را می‌توان به زیر نوشت:

$$ Fi = x \times \frac { ۱ } { ۵ } $$

• Fi: خمس عدد مورد نظر
• x: عدد مورد نظر

خمس یا همان $$ \frac { ۱ } { ۵ } $$، یک کسر واحد (با صورت ۱) است. بنابراین، با ضرب هر عدد در آن، صورت کسر برابر با همان عدد می‌شود:

۵ ÷ عدد = خمس عدد مورد نظر

$$ Fi = \frac { x } { ۵ } $$

به این ترتیب می‌توانیم بگوییم که خمس هر عدد، از تقسیم آن عدد بر ۵ به دست می‌آید. نحوه استفاده از فرمول‌های خمس را با حل یک مثال توضیح می‌دهیم.

مثال ۱: محاسبه خمس عدد

خمس عدد ۲۵ را به دست بیاورید.

خمس عدد ۲۵، برابر با یک‌پنجم آن یا حاصل تقسیم این عدد بر ۵ است:

۵ ÷ ۲۵ = خمس عدد ۲۵

۵ = خمس عدد ۲۵

بنابراین، خمس عدد ۲۵ برابر با ۵ است. در این مثال، از یک عدد برای نمایش مفهوم خمس استفاده کردیم. در دنیای واقعی، خمس برای تقسیم هر چیزی به کار برود. به عنوان مثال، شخصی که یک‌پنجم درآمد خود را به پس‌انداز اختصاص می‌دهد، در واقع از مفهوم خمس برای مدیریت دارایی‌های خود استفاده می‌کند. بنابراین، اعداد ریاضی، شاید کمی پیچیده و غیر قابل درک به نظر بیایند اما به راحتی در مثال‌های دنیای واقعی قابل مشاهده هستند.

مثال ۲ : محاسبه خمس ساعت

خمس هر ساعت، چند دقیقه می شود؟

هر ساعت، ۶۰ دقیقه است. برای به دست آوردن خمس ساعت، باید این عدد را بر ۵ تقسیم کرد.

بنابراین داریم:

۵ ÷ ۶۰ = خمس ساعت

۱۲ = خمس ساعت

در نتیجه، خمس هر ساعت، برابر با ۱۲ دقیقه است.

خمس با نصف، ثلث و ربع چه تفاوتی دارد ؟

نصف، ثلث و ربع، از شناخته شده‌ترین نسبت‌های واحد در دنیای ریاضی هستند. تفاوت اصلی خمس با این نسبت‌ها، در مخرج کسر آن‌ها است. نصف یا نیم، یک‌دوم یا عدد $$ \frac { ۱ } { ۲ } $$ را نمایش می‌دهد. به عنوان مثال، نیم‌دایره زیر را در نظر بگیرید.

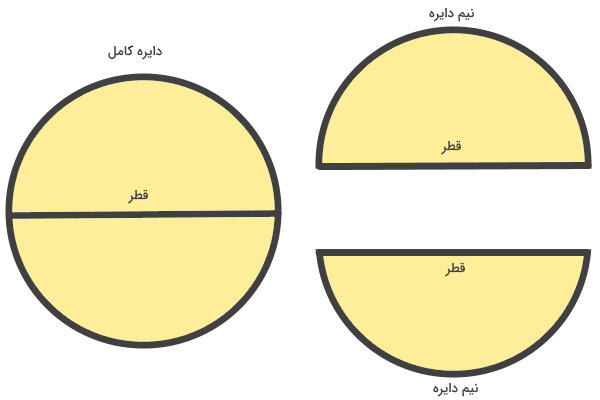
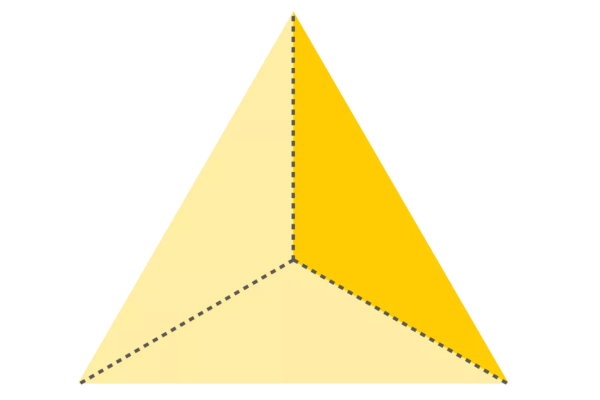
نیم‌دایره، از تقسیم یک دایره کامل به دو قسمت مساوی، یا به عبارت دیگر، نصف کردن دایره کامل به دست می‌آید. هر نیم‌دایره، نصف دایره کامل یا یک‌دوم آن است. ثلث، به عنوان یک‌سوم یا عدد $$ \frac { ۱ } { ۳ } $$ در نظر گرفته می‌شود. اتصال راس‌های یک مثلث متساوی‌الاضلاع به مرکز آن، این شکل را به سه قسمت تقسیم می‌کند. هر قسمت، ثلث مثلث متساوی‌الاضلاع به شمار می‌رود.

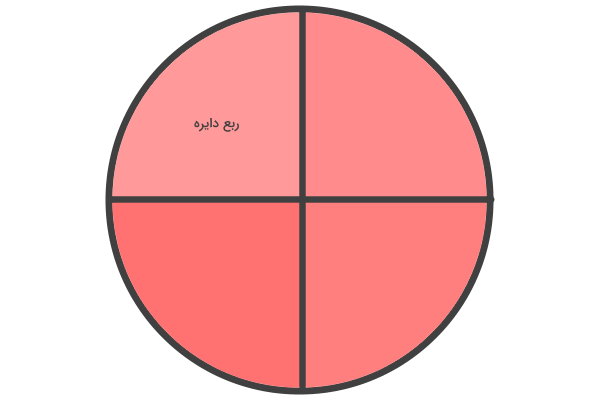
ربع، یک‌چهارم یا عدد $$ \frac { ۱ } { ۴ } $$ است. با رسم دو قطر عمود بر هم، دایره به چهار قسمت مساوی تقسیم می‌شود. هر قسمت، ربع دایره یا یک‌چهارم دایره کامل را نمایش می‌دهد.

مثال ۳: محاسبه نصف خمس

نصف خمس عدد ۳۰ را حساب کنید.

نصفِ خمس، از ضرب عدد $$ \frac { ۱ } { ۲ } $$ در خمس یک عدد به دست می‌آید. برای تعیین نصف خمس عدد ۳۰، ابتدا خمس آن را محاسبه می‌کنیم. این مقدار برابر با حاص‌ضرب عدد $$ \frac { ۱ } { ۵ } $$ در عدد ۳۰ است:

$$ \frac { ۱ } { ۵ } \times ۳۰ $$ = خمس عدد ۳۰

$$ \frac { ۳۰ } { ۵ } $$ = خمس عدد ۳۰

۶ = خمس عدد ۳۰

اکنون، نوبت به محاسبه نصف خمس عدد ۳۰ می‌رسد. به این منظور، عدد ۶ (خمس عدد ۳۰) را در $$ \frac { ۱ } { ۲ } $$ ضرب می‌کنیم:

$$ \frac { ۱ } { ۲ } \times ۶ $$ = نصف خمس عدد ۳۰

$$ \frac { ۶ } { ۲ } $$ = نصف خمس عدد ۳۰

۳ = نصف خمس عدد ۳۰

در نتیجه، نصف خمس عدد ۳۰ برابر با ۳ است. یکی دیگر از روش‌های به دست آوردن نسبت‌های تو در تو مانند این مثال، ضرب عدد کسری آن‌ها در هم و در عدد مورد نظر است. بر اساس این روش، نصف خمس عدد ۳۰ به صورت زیر محاسبه می‌شود:

$$ \frac { ۱ } { ۲ } \times \frac { ۱ } { ۵ } \times ۳۰ $$ = نصف خمس عدد ۳۰

$$ \frac { ۱ \times ۱ \times ۳۰ } { ۲ \times ۵ } $$ = نصف خمس عدد ۳۰

$$ \frac { ۳۰ } { ۱۰ } $$ = نصف خمس عدد ۳۰

۳ = نصف خمس عدد ۳۰

مثال ۴: محاسبه نصف ثلث خمس

نصف ثلث خمس عدد ۲۲۵ چند می‌شود؟

برای محاسبه نصف ثلث خمس عدد ۲۲۵، ابتدا یکی از نسبت‌ها را به دست می‌آوریم. سپس، نتیجه به دست آمده را در نسبت بعدی ضرب می‌کنیم. خمس عدد ۲۲۵ برابر است با:

۵ ÷ ۲۲۵ = خمس عدد ۲۲۵

۴۵ = خمس عدد ۲۲۵

اکنون، ثلث این عدد را با استفاده از رابطه زیر به دست می‌آوریم:

۳ ÷ ۴۵ = ثلث عدد ۴۵

۱۵ = ثلث عدد ۴۵

بنابراین، ثلث خمس عدد ۲۲۵ برابر با ۱۵ است. در مرحله آخر، نصف این عدد را محاسبه می‌کنیم:

۲ ÷ ۱۵ = نصف عدد ۱۵

۷/۵ = نصف عدد ۱۵

در نتیجه، نصف ثلث خمس عدد ۲۲۵ برابر با ۷/۵ می‌شود. فرمول‌‌های زیر، نحوه محاسبه مستقیم این عدد را نمایش می‌دهند:

$$ \frac { ۱ } { ۲ } \times \frac { ۱ } { ۳ } \times \frac { ۱ } { ۵ } \times ۲۲۵ $$ = نصف ثلث خمس ۲۲۵

$$ \frac { ۲۲۵ } { ۲ \times ۳ \times ۵ } $$ = نصف ثلث خمس ۲۲۵

$$ \frac { ۲۲۵ } { ۳۰ } $$ = نصف ثلث خمس ۲۲۵

۷/۵ = نصف ثلث خمس ۲۲۵

خمس در اشکال هندسی

یکی از کاربردهای مفهوم خمس، تقسیم‌بندی اشکال هندسی به پنج قسمت مساوی است. خمس اشکال هندسی معمولا با توجه به مساحت‌شان تعیین می‌شود. نمایش خمس بر روی اغلب اشکال، کار ساده‌ای نیست و نیاز به دقت دارد. با این وجود، خمس برخی از اشکال نظیر دایره، مستطیل و پنج‌ضلعی منتظم، از قواعد خاصی پیروی می‌کند که در این بخش به طور خلاصه آن‌ها را مرور می‌کنیم.

خمس در دایره

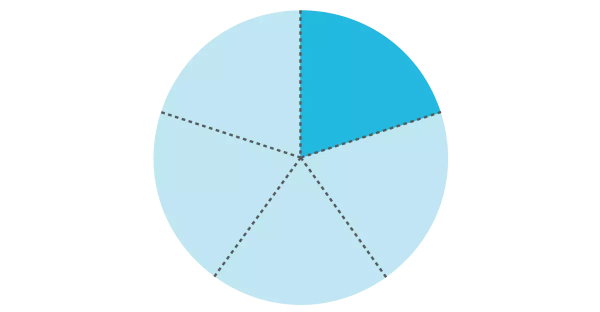
دایره، یک منحنی بسته با زاویه مرکزی ۳۶۰ درجه است. برای نمایش مفهوم خمس در دایره می‌توانیم زاویه مرکزی آن را بر عدد ۵ تقسیم کنیم:

۷۲ = ۵ ÷ ۳۶۰

به این ترتیب، خمس زاویه مرکزی دایره برابر با ۷۲ درجه است. از این زاویه، برای تعیین خمس دایره استفاده می‌کنیم. تصویر زیر، دایره‌ای متشکل از ۵ قطاع با زاویه ۷۲ درجه را نمایش می‌دهد. هر قطاع، خمس دایره است.

خمس در مستطیل

رسم خمس شکل مستطیل و مربع (یکی از حالت‌های خاص مستطیل)، با تقسیم‌بندی طول‌ها یا عرض‌ها به پنج قسمت مساوی و اتصال آن‌ها به یکدیگر انجام می‌گیرد.

خمس در پنج ضلعی منتظم

پنج‌ضلعی منتظم، از پنج ضلع هم‌اندازه و پنج زاویه داخلی هم‌اندازه تشکیل می‌شود. اگر راس‌های این چندضلعی منتظم را به مرکز آن وصل کنیم، پنج مثلث مساوی به وجود می‌آیند. هر مثلث، خمس پنج‌ضلعی منتظم است.

مثال های خمس در ریاضی

در این بخش، به منظور درک بهتر مبحث خمس در ریاضی، به حل چندین مثال متنوع می‌پردازیم.

مثال ۵: محاسبه مجموع نسبت های ساعت

مجموع خمس، ربع و ثلث ساعت چند می‌شود؟

در مثال‌های قبلی، خمس هر ساعت را برابر با ۱۲ دقیقه به دست آوردیم:

$$ \frac { ۱ } { ۵ } \times ۶۰ $$ = خمس هر ساعت

$$ \frac { ۶۰ } { ۵ } $$ = خمس هر ساعت

۱۲ = خمس هر ساعت

ربع هر ساعت، با استفاده از رابطه زیر محاسبه می‌شود:

$$ \frac { ۱ } { ۴ } \times ۶۰ $$ = ربع هر ساعت

$$ \frac { ۶۰ } { ۴ } $$ = ربع هر ساعت

۱۵ = ربع هر ساعت

فرمول محاسبه ثلث هر ساعت نیز برابر است با:

$$ \frac { ۱ } { ۳ } \times ۶۰ $$ = ثلث هر ساعت

$$ \frac { ۶۰ } { ۳ } $$ = ثلث هر ساعت

۲۰ = ثلث هر ساعت

پس از به دست آوردن مقادیر خمس، ربع و ثلث، آن‌ها را با یکدیگر جمع می‌کنیم:

۲۰+ ۱۵ + ۱۲ = مجموع خمس، ربع و ثلث هر ساعت

۴۷ = مجموع خمس، ربع و ثلث هر ساعت

مثال ۶: محاسبه خمس محیط دایره

دایره‌ای به قطر ۴۰ سانتی‌متر را در نظر بگیرید. خمس محیط این دایره را به دست بیاورید.

فرمول محاسبه محیط دایره، عبارت است از:

$$ C = ۲ \pi r $$

• C: محیط دایره
• π: عدد ثابت پی برابر ۳/۱۴
• r: شعاع دایره (نصف قطر) برابر با ۲۰ سانتی‌متر

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم و آن را حل می‌کنیم:

$$ C = ۲ \times ۳/۱۴ \times ۲۰ $$

$$ C = ۱۲۵/۶ $$

محیط دایره کامل برابر با ۱۲۵/۶ است. خمس این محیط از رابطه زیر به دست می‌آید:

$$ ۱۲۵/۶ \times \frac { ۱ } { ۵ } $$ = خمس محیط دایره

$$ \frac { ۱۲۵/۶ } { ۵ } $$ = خمس محیط دایره

۲۵/۱۲ = خمس محیط دایره

در نتیجه، خمس محیط دایره‌ای با شعاع ۲۰ سانتی‌متر برابر با ۲۵/۱۲ سانتی‌متر است.

مثال ۷: محاسبه خمس زمین

شخصی زمینی به مساحت ۱۷۵۰ متر مربع را در اختیار دارد. او می‌خواهد خمس زمین خود را به ساخت یک اقامتگاه شخصی و باقی آن را به ساخت باغ اختصاص دهد. مساحت زمین اختصاص داده شده به باغ خواهد بود؟

مساحت باغ، از اختلاف مساحت کل زمین با مساحت اقامتگاه به دست می‌آید:

مساحت اقامتگاه - مساحت کل زمین = مساحت باغ

مساحت اقامتگاه، خمس مساحت کل زمین است. از این‌رو، رابطه بالا به شکل زیر درمی‌آید:

خمس مساحت کل زمین - مساحت کل زمین = مساحت باغ

خمس مساحت کل زمین به صورت زیر محاسبه می‌شود:

۵ ÷ مساحت کل زمین = خمس مساحت کل زمین

مقدار مساحت زمین (۱۷۵۰ متر مربع) را درون رابطه بالا قرار می‌دهیم:

۵ ÷ ۱۷۵۰ = خمس مساحت کل زمین

۳۵۰ = خمس مساحت کل زمین

خمس مساحت کل زمین برابر با ۳۵۰ متر مربع است. این مقدار را از مساحت کل زمین کم می‌کنیم تا مساحت باغ به دست بیاید:

۱۴۰۰ = ۳۵۰ - ۱۷۵۰ = مساحت باغ

در نتیجه، مساحت باغ برابر با ۱۴۰۰ متر مربع خواهد بود.

مثال ۸: محاسبه خمس پس‌ انداز سالانه

درآمد ماهانه شخصی، برابر با ۱۲ واحد است. اگر او از ابتدای سال، خمس درآمد خود را پس‌انداز کند، در انتهای سال، پس‌اندازه سالانه او به چند واحد می‌رسد؟ در صورت اختصاص خمس پس‌انداز سالانه به خریدهای عید، چه مقدار از پس‌انداز شخص کم می‌شود؟

یک سال، برابر با ۱۲ ماه است. بنابراین، میزان پس‌انداز ماهانه شخص، از رابطه زیر محاسبه می‌شود:

خمس درآمد ماهانه × ۱۲ = پس‌انداز سالانه

مس درآمد ماهانه شخص از رابطه زیر به دست می‌آید:

۵ ÷ درآمد ماهانه = خمس درآمد ماهانه

۵ ÷ ۱۲ = خمس درآمد ماهانه

۲/۴ = خمس درآمد ماهانه

این عدد را در رابطه پس‌انداز سالانه قرار می‌دهیم:

۲/۴ × ۱۲ = پس‌انداز سالانه

۲۸/۸ = پس‌انداز سالانه

در نتیجه، پس‌انداز شخص در انتهای سال به ۲۸/۸ واحد می‌رسد. اکنون، به سراغ بخش دوم سوال می‌رویم. شخص، قصد دارد خمس پس‌انداز خود را به خریدهای عید اختصاص دهد. این مقدار، از تقسیم عدد بالا بر ۵ محاسبه می‌شود:

۵ ÷ پس‌انداز سالانه = خمس پس‌انداز سالانه

۵ ÷ ۲۸/۸ = خمس پس‌انداز سالانه

۵/۷۶ = خمس پس‌انداز سالانه

به این ترتیب، ۵/۷۶ واحد از پس‌اندازه شخص برای خرید عید کم می‌شود.

مثال ۹: محاسبه نصف ثلث ربع خمس

نصف ثلث ربع خمس عدد ۳۹۰ را تعیین کنید.

محاسبه خود را با تعیین خمس شروع می‌کنیم. این مقدار، برابر با یک‌پنجم عدد ۳۹۰ است:

$$ \frac { ۱ } { ۵ } $$ × ۳۹۰ = خمس عدد ۳۹۰

$$ \frac { ۳۹۰ } { ۵ } $$ = خمس عدد ۳۹۰

۷۸ = خمس عدد ۳۹۰

در قدم بعدی، به سراغ محاسبه ربع خمس عدد ۳۹۰ یا همان ربع عدد ۷۸ می‌رویم:

$$ \frac { ۱ } { ۴ } $$ × ۷۸ = ربع خمس عدد ۳۹۰

$$ \frac { ۷۸ } { ۴ } $$ = ربع خمس عدد ۳۹۰

۱۹/۵ = ربع خمس عدد ۳۹۰

اکنون، نوبت به محاسبه ثلث ربع خمس عدد ۳۹۰ یا همان ثلث عدد ۱۹/۵ می‌رسد:

$$ \frac { ۱ } { ۳ } $$ × ۱۹/۵ = ثلث ربع خمس عدد ۳۹۰

$$ \frac { ۱۹/۵ } { ۳ } $$ = ثلث ربع خمس عدد ۳۹۰

۶/۵ = ثلث ربع خمس عدد ۳۹۰

در نهایت، با تعیین یک‌دوم مقدار بالا، نصف ثلث ربع خمس عدد ۳۹۰ به دست می‌آید:

$$ \frac { ۱ } { ۲ } $$ × ۶/۵ = نصف ثلث ربع خمس عدد ۳۹۰

$$ \frac { ۶/۵ } { ۲ } $$ = نصف ثلث ربع خمس عدد ۳۹۰

۳/۲۵ = نصف ثلث ربع خمس عدد ۳۹۰

مثال ۱۰: محاسبه خمس عدد کسری

خمس عدد کسری $$ \frac { ۵ } { ۳ } $$، کدام یک از نسبت‌های معروف است؟

به منظور تعیین خمس یک عدد کسری، آن را در $$ \frac { ۱ } { ۵ } $$ ضرب می‌کنیم. این کار، با استفاده از اصول ضرب کسرها انجام می‌گیرد. در ضرب کسرها، صورت دو کسر در یکدیگر و مخرج آن‌ها نیز در یکدیگر ضرب می‌شود. با توجه به توضیحات ارائه شده، خمس $$ \frac { ۵ } { ۳ } $$ برابر است با:

$$ \frac { ۵ } { ۳ } \times \frac { ۱ } { ۵ } $$ = خمس پنج‌سوم

$$ \frac { ۵ \times ۱ } { ۳ \times ۵ } $$ = خمس پنج‌سوم

$$ \frac { ۵ } { ۱۵ } $$ = خمس پنج‌سوم

$$ \frac { ۱ } { ۳ } $$ = خمس پنج‌سوم

خمس عدد پنج‌سوم برابر با یک‌سوم یا همان ثلث است.

مثال ۱۱: جمع نسبت ها

حاصل‌جمع ربع خمس ۶۶ با ثلث ربع ۶۶ را محاسبه کنید.

ربع خمس عدد ۶۶، از رابطه زیر محاسبه می‌شود:

$$ \frac { ۱ } { ۴ } \times \frac { ۱} { ۵ } \times ۶۶ $$ = ربع خمس ۶۶

$$ \frac { ۶۶ } { ۴ \times ۵ } $$ = ربع خمس ۶۶

$$ \frac { ۶۶ } { ۲۰ } $$ = ربع خمس ۶۶

$$ ۳/۳ $$ = ربع خمس ۶۶

ثلث ربع ۶۶ نیز از رابطه زیر به دست می‌آید:

$$ \frac { ۱ } { ۳ } \times \frac { ۱} { ۴ } \times ۶۶ $$ = ثلث ربع ۶۶

$$ \frac { ۶۶ } { ۳ \times ۴ } $$ = ثلث ربع ۶۶

$$ \frac { ۶۶ } { ۱۲ } $$ = ثلث ربع ۶۶

$$ ۵/۵ $$ = ثلث ربع ۶۶

حاصل‌جمع این دو نسبت برابر است با:

۸/۸ = ۵/۵ + ۳/۳

مثال ۱۲: محاسبه خمس از روی ربع

ربع عددی برابر با ۲۴ است. خمس آن عدد را بیابید.

ربع، همان یک‌چهارم است. بنابراین، برای به دست آوردن خمس عدد، ابتدا مقدار عدد را از روی ربع آن تعیین می‌کنیم. به این ترتیب، داریم:

۴ ÷ عدد = ربع عدد

۴ ÷ عدد = ۲۴

۴ × ۲۴ = عدد

۹۶ = عدد

با دانستن مقدار عدد و تقسیم آن بر عدد ۵، خمس عدد به دست می‌آید:

۵ ÷ عدد = خمس عدد

۵ ÷ ۹۶ = خمس عدد

۱۹/۲ = خمس عدد

مثال ۱۳: مقایسه نسبت ها

بین خمس عدد ۱۴۰ یا ربع عدد ۱۲۰، کدامیک بزرگ‌تر است؟

در کسرهای واحد، هرچه مخرج کسر بزرگ‌تر شود، اندازه کسر کوچک‌تر خواهد شد. بنابراین، برای یک عدد، ربع (یک‌چهارم) آن عدد همیشه از خمس (یک‌پنجم) آن بزرگ‌تر است. این مثال، خمس و ربع دو عدد متفاوت را از ما می‌خواهد. خمس عدد ۱۴۰ برابر است با:

$$ \frac { ۱ } { ۵ } \times ۱۴۰ $$ = خمس عدد ۱۴۰

$$ \frac { ۱۴۰ } { ۵ } $$ = خمس عدد ۱۴۰

۲۸ = خمس عدد ۱۴۰

ربع عدد ۱۲۰، به صورت زیر محاسبه می‌شود:

$$ \frac { ۱ } { ۴ } \times ۱۲۰ $$ = خمس عدد ۱۲۰

$$ \frac { ۱۲۰ } { ۴ } $$ = خمس عدد ۱۲۰

۳۰ = خمس عدد ۱۲۰

خمس عدد ۱۴۰ برابر با ۲۸ و ربع عدد ۱۲۰ برابر با ۳۰ شد. در نتیجه، ربع ۱۲۰ از خمس ۱۴۰ بزرگ‌تر است.

آزمون سنجش یادگیری خمس در ریاضی

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث خمس در ریاضی را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.