محاسبه حجم حاصل از دوران — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در این مطلب قصد داریم تا روش محاسبه حجم حاصل از دوران نمودار حول محوری مشخص را توضیح دهیم. از این رو پیشنهاد می‌کنیم قبل از مطالعه این مطلب، مبحث انتگرال را مطالعه فرمایید.

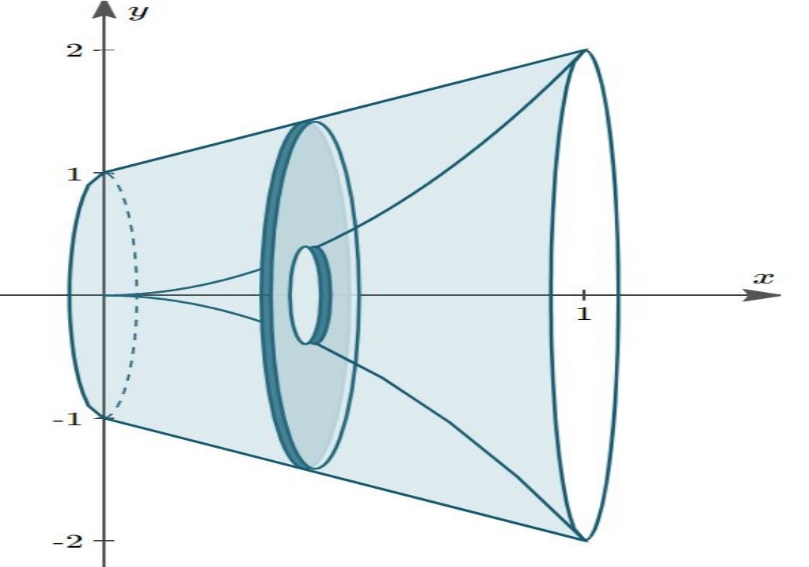
فرمول حجم جسم دوار

اجازه دهید تا در ابتدا منظورمان را از جسم دوار و حجم جسم دوار بیان کنیم. بدین منظور در ابتدا نمودار همچون $$y = f \left ( x \right )$$ را به صورت زیر در نظر بگیرید.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

حال تصور کنید نمودار فوق، حول محور x دوران کند. در این صورت حجمی سه‌بعدی مطابق با شکل زیر بدست خواهد آمد.

هدف ما در این مطلب محاسبه حجم بدست آمده در شکل فوق است. حجم مدنظر در هر مقطع، برابر با حاصل‌ضرب مساحت سطح مقطع در آن نقطه در ضخامت است. به عبارتی دیفرانسیل حجم برابر است با:

$$\large d V = A ( x ) d x$$

با انتگرال‌گیری از رابطه فوق از بازه a تا b کل حجم به صورت زیر بدست خواهد آمد.

$$\large \boxed { V = \int _ { { \, a } } ^ { { \, b } } { { A \left ( x \right ) \, d x } } }$$

با همین استدلال حجم دوران یافته حول محور y را می‌توان به صورت زیر بدست آورد.

$$\large \boxed { V = \int _ { { \, c } } ^ { { \, d } } { { A \left ( y \right ) \, d y } } }$$

به این روش اصطلاحا، «روش حلقه» (Method of Ring) یا «روش دیسک» (Method of Disk) گفته می‌شود. در حقیقت مساحت محصور در حلقه‌های دایره‌ای، محاسبه شده و با ضرب آن در دیفرانسیل طول، حجم بدست می‌آید.

بدست آوردن مساحت

به منظور بدست آوردن مساحت $$A ( x )$$ یا $$A ( y )$$ روش‌های بسیاری وجود دارد. بدست آوردن مساحت‌ها وابسته به انتخاب محور دوران است. در حالت کلی برای بدست آوردن مساحت، از فرمول $$A = \pi r ^ 2$$ استفاده می‌شود. در این رابطه r وابسته به محور دوران و تابع دوران یافته است. برای نمونه در شکل ۱ مساحت هر دیسک برابر با $$A = \pi { f ( x ) } ^ 2$$ است.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

مثال ۱

حجم حاصل از دوران منحنی $$y = { x ^ 2 } - 4 x + 5$$ را در بازه x=1 تا x=4 بدست آورید.

به منظور حل این گونه سوالات در ابتدا نمودار را رسم کرده و شکل دوران یافته‌ی آن‌ را حول محور خواسته شده، تصور کنید. در شکل زیر مساحت محصور به نمودار و حجم ایجاد شده در نتیجه دوران آن نشان داده شده‌اند.

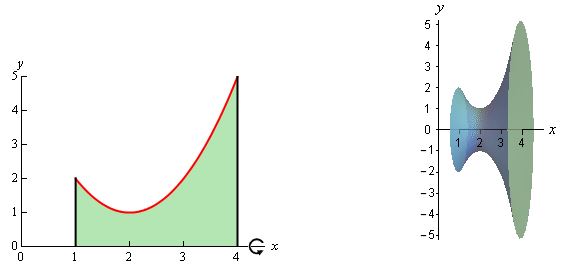
در شکل زیر مساحت یک مقطع از حجم نشان داده شده در بالا، ترسیم شده است. همان‌طور که می‌بینید، فاصله نمودار از محور که برابر با مقدار y است، شعاع دیسک را نشان می‌دهد.

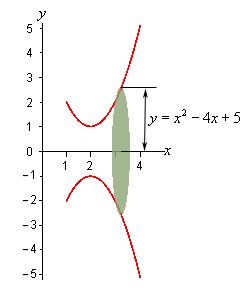
با توجه به تصویر فوق، مساحتِ (A(x برابر است با:

$$\large A \left ( x \right ) = \pi \underbrace { { \left ( { { x ^ 2 } - 4 x + 5 } \right ) ^ 2 } } _ y = \pi \left ( { { x ^ 4 } - 8 { x ^ 3 } + 2 6 { x ^ 2 } - 4 0 x + 2 5 } \right )$$

بدیهی است که اولین دیسک در x=1 و آخرینشان در x=4 قرار گرفته است. بنابراین بازه‌ی انتگرال‌گیری در این فاصله قرار دارد. نهایتا حجم جسم دوار به کمک انتگرال محاسبه می‌شود.

$$\large \begin {align*} V &= \int _ { { \, a } } ^ { { \, b } } { { A \left ( x \right ) \, d x } } \\ & = \pi \int _ { { \, 1 } } ^ { { \, 4 } } { { { x ^ 4 } - 8 { x ^ 3 } + 2 6 { x ^ 2 } - 4 0 x + 2 5 \, d x } } \\ & = \pi \left. { \left ( { \frac { 1 } { 5 } { x ^ 5 } - 2 { x ^ 4 } + \frac { { 2 6 } } { 3 } { x ^ 3 } - 2 0 { x ^ 2 } + 2 5 x } \right ) } \right| _ 1 ^ 4 \\ & = \frac { { 7 8 \pi } } { 5 } \end {align*}$$

در مثال ارائه شده در بالا یک نمودار دوران پیدا کرد. در حالتی دیگر ممکن است فضای بین دو نمودار،‌ حول محوری مشخص دوران کند. در این شرایط در انتخاب r باید دقت شود. معمولا r را می‌توان برابر با اختلاف مساحت دو دیسک در نظر گرفت. در ادامه مثالی ذکر شده که مطالعه آن را توصیه می‌کنیم.

مثال ۲

ناحیه بین دو نمودار $$y = \sqrt[3]{x}$$ و $$y = \frac { x } { 4 }$$ را حول محور y دوران می‌دهیم. حجم جسم بدست آمده چقدر است؟

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

هما‌ن‌طور که در مثال ۱ نیز بیان شد، در ابتدا باید درکی درست از فضای بیان شده و حجم ناشی شده در نتیجه دوران داشته باشید. در ادامه مساحت مدنظر و حجم دوران یافته‌‌ی آن نشان داده شده است.

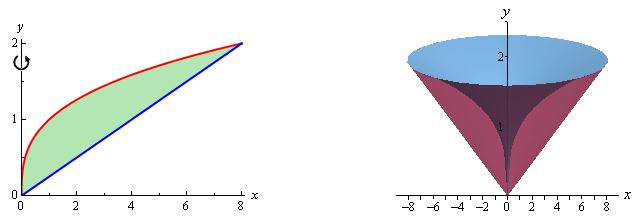
در این مثال فضای بین دو نمودار حول محور y دوران یافته است؛ بنابراین بهتر است تا x را به صورت زیر بر حسب y بیان کنیم.

$$\large \begin {align*} y & = \sqrt [ 3 ] { x } \hspace {0.5in} \ \Rightarrow \hspace {0.5in} x = { y ^ 3 } \\ y & = \frac { x } { 4 } \hspace {0.65in} \Rightarrow \hspace {0.5in} x = 4 y \end {align*}$$

بدیهی است که مساحت هر مقطع از جسم برابر با اختلاف مساحت ایجاد شده در نتیجه دوران هریک از نمودار‌ها است. در شکل زیر مساحت یک مقطع از جسم ایجاد شده، نشان داده شده است.

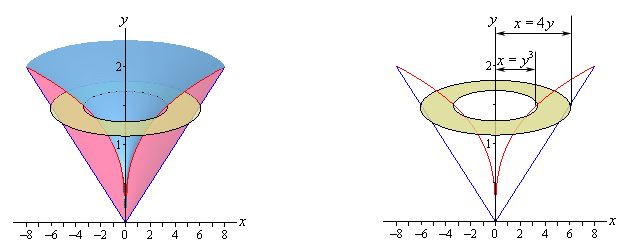
با توجه به شکل فوق، مساحت مقاطع، بر حسب y به صورت زیر تغییر می‌کنند.

$$\large A \left ( y \right ) = \pi \left ( { { { \left ( { 4 y } \right ) } ^ 2 } - { { \left ( { { y ^ 3 } } \right ) } ^ 2 } } \right ) = \pi \left ( { 1 6 { y ^ 2 } - { y ^ 6 } } \right )$$

پایین‌ترین مقطع در y=0 و بالاترین آن‌ها در y=2 قرار دارد. بنابراین حجم ناشی از دوران به صورت زیر بدست می‌آید.

$$\large \begin {align*} V &= \int _ { { \, c } } ^ { { \, d } } { { A \left ( y \right ) \, d y } } \\ & = \pi \int _ { { \, 0 } } ^ { { \, 2 } } { { 1 6 { y ^ 2 } - { y ^ 6 } \, d y } } \\ & = \pi \left. { \left ( { \frac { { 1 6 } } { 3 }{ y ^ 3 } - \frac { 1 } { 7 } { y ^ 7 } } \right ) } \right | _ 0 ^ 2 \\ & = \frac { { 5 1 2 \pi } }{ { 2 1 } } \end {align*}$$

نکته: بهتر است که در هنگام دوران تابع حول خطوط y=a، تابعِ تحت انتگرال بر حسب x بیان شود. بر همین مبنا هنگامی که تابع حول محور x=b دوران کند، تابع باید بر حسب y ارائه شود.

مثال ۳

ناحیه قرار گرفته بین دو نمودار $$y = { x ^ 2 } - 2 x$$ و $$y = x$$ را در نظر بگیرید. فرض کنید این ناحیه حول محور y=4 دوران کند. در این صورت حجم جسم بدست آمده، چقدر است؟

ناحیه بین دو نمودار و حجم دوران یافته برابرند با:

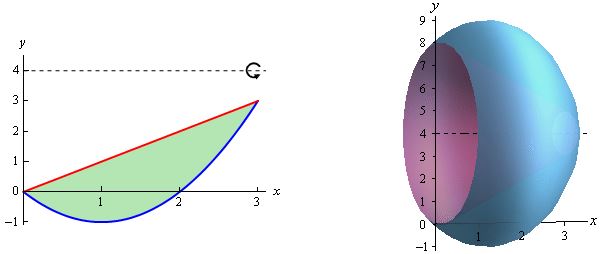
با توجه به نکته بیان شده در بالا، تابعِ تحت انتگرال باید بر حسب x بیان شود. مقاطع ایجاد شده مطابق با شکل زیر، حلقه‌هایی هستند که موازی محور y قرار گرفته‌اند.

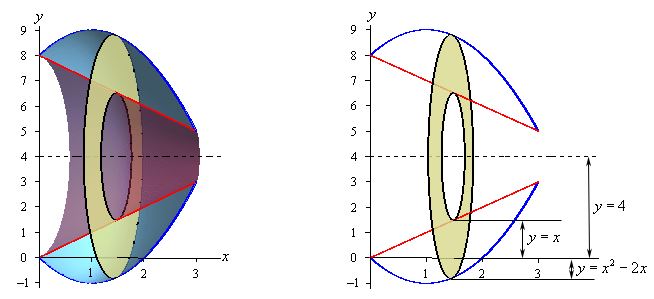
توجه داشته باشید که شعاع‌های این حلقه‌ها برابر با فاصله دو تابع از محور y=4 هستند. بنابراین شعاع داخلی (r_i) و شعاع خارجی (r_o) به صورت زیر بدست می‌آیند.

$$\large r _ i = 4 - x \ \ , \ \ r _ o = 4- ( x ^ 2 - 2 x ) = - x ^ 2 + 2 x + 4$$

با بدست آمدن شعاع‌های داخلی و خارجی، مساحت حلقه‌ها را نیز می‌توان به صورت زیر بدست آورد.

$$\large A \left( x \right) = \pi \left ( { { { \left ( { - { x ^ 2 } + 2 x + 4 } \right ) } ^ 2 } - { { \left ( { 4 - x } \right ) } ^ 2 } } \right ) = \pi \left ( { { x ^ 4 } - 4 { x ^ 3 } - 5 { x ^ 2 } + 2 4 x } \right )$$

اولین حلقه در x=0 و آخرین آن‌ها در x=3 قرار گرفته؛ بنابراین حجم حاصل از دوران نمودار برابر است با:

$$\large \begin {align*} V & = \int _ { { \, a } } ^ { { \, b } } { { A \left ( x \right ) \, d x } } \\ & = \pi \int _ { { \, 0 } } ^ { { \, 3 } } { { { x ^ 4 } - 4 { x ^ 3 } - 5 { x ^ 2 } + 2 4 x \, d x } } \\ & = \pi \left. { \left ( { \frac { 1 } { 5 } { x ^ 5 } - { x ^ 4 } - \frac { 5 } { 3 } { x ^ 3 } + 1 2 { x ^ 2 } } \right ) } \right | _ 0 ^ 3 \\ & = \frac { { 1 5 3 \pi } } { 5 } \end {align*}$$

مثال ۴

حجم حاصل از دوران ناحیه بین $$y = 2 \sqrt { x - 1 }$$ و $$y = { x - 1 }$$ حول محور $$x = - 1$$ را محاسبه کنید.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

در ادامه ناحیه بیان شده و حجم ناشی از دوران نشان داده شده است.

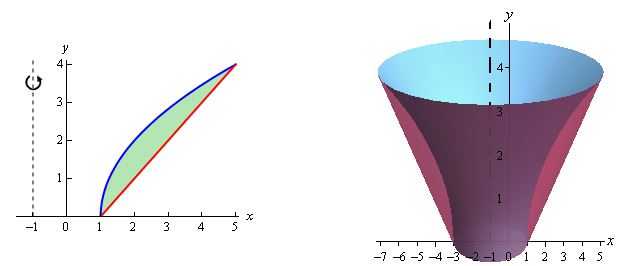
محور دوران، $$x = - 1$$ است؛ لذا تابع نیز باید بر حسب x بیان شود.

$$\large \begin {align*} y &= 2 \sqrt { x - 1 } \hspace {0.5in} \Rightarrow \hspace {0.5in} x = \frac { { { y ^ 2 } } } { 4 } + 1 \\ y & = x - 1 \hspace {0.75in} \Rightarrow \hspace {0.5in} x = y + 1 \end {align*}$$

در صورتی که با نحوه معکوس کردن توابع آشنا نیستید، می‌توانید این مطلب را مطالعه فرمایید. در ادامه باید شکل حلقه‌ها را مشخص کرده و شعاع‌های داخلی و خارجی آن‌ها را بدست آورید. در تصویر زیر، حلقه‌های دوران یافته نشان داده شده‌اند.

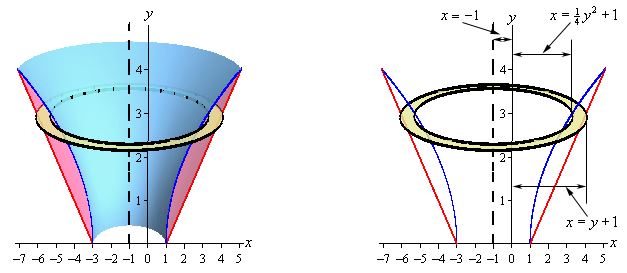
مشابه با مثال قبل، شعاع‌های داخلی و خارجیِ حلقه‌های بالا برابرند‌ با:

$$\large \begin{align*} r _ o & = y + 1 + 1 = y + 2\\ r _ i & = \frac{{{y^2}}}{4} + 1 + 1 = \frac{{{y^2}}}{4} + 2\end{align*}$$

با توجه به این دو شعاع، مساحت حلقه‌های ایجاد شده، برابرند با:

$$\large A \left ( y \right ) = \pi \left ( { { { \left ( { y + 2 } \right ) } ^ 2 } - { { \left ( { \frac { { { y ^ 2 } } } { 4 } + 2 } \right ) } ^ 2 } } \right ) = \pi \left ( { 4 y - \frac { { { y ^ 4 } } } { { 1 6 } } } \right )$$

اولین حلقه در y=0 و آخرین حلقه در y=4 قرار گرفته‌اند. بنابراین حاصل انتگرال حجمی برابر است با:

$$\large V = \int _{ { \, c } } ^ { { \, d } } { { A \left ( y \right ) \, d y } } = \pi \int _ { { \, 0 } } ^ { { \, 4 } } { { 4 y - \frac { { { y ^ 4 } } } { { 1 6 } } \, d y } } = \pi \left. { \left ( { 2 { y ^ 2 } - \frac { 1 } { { 8 0 } }{ y ^ 5 } } \right ) } \right | _ 0 ^ 4 = \frac { { 9 6 \pi } } { 5 }$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• مجموعه آموزش‌های دروس دبیرستان و پیش‌دانشگاهی
• مختصات قطبی — از صفر تا صد
• مساحت در مختصات قطبی — به زبان ساده
• مساحت سطح حاصل از دوران — به زبان ساده

^^