جریان یکنواخت در کانال باز – به زبان ساده

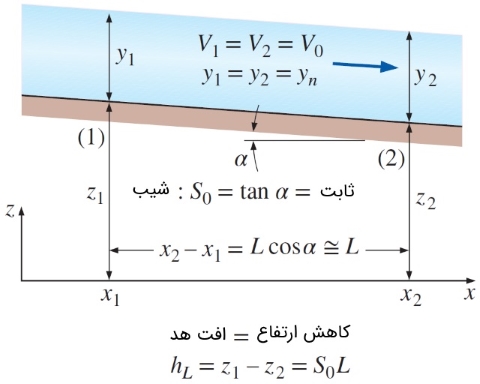
پیش‌تر در مجله فرادرس، جریان در کانال باز را بررسی و انواع آن را معرفی کردیم. نوعی از جریان که در آن عمق جریان ثابت بماند، جریان یکنواخت (Uniform Flow) نامیده می‌شود. در عمل برای اینکه جریانی یکنواخت باشد، نیاز به کانال‌هایی با طول زیاد و شیب و سطح مقطع ثابت داریم و جنس روکش کانال باید یکسان باشد. در طراحی کانال‌های باز، مطلوب است که همه جا جریان یکنواخت باشد. زیرا در این صورت، ارتفاع دیواره کانال تغییر نمی‌کند و طراحی و ساخت آن نیز راحت‌تر خواهد بود.

عمق در جریان یکنواخت را عمق قائم (Normal Depth) نامیده و آن را با $$\large y_n$$ نشان می‌دهیم. از طرف دیگر، $$\large V_0$$ نیز برای نشان دادن سرعت متوسط جریان به کار می‌رود و سرعت جریان یکنواخت (Uniform Flow Velocity) نام دارد. به شکل زیر توجه کنید. تا زمانی که شیب، سطح مقطع و سختی سطح کانال تغییر نکند، جریان یکنواخت باقی خواهد ماند. با زیاد شدن شیب سطح زیرین کانال، سرعت جریان بیشتر شده و عمق آن نیز افزایش می‌یابد. در نتیجه، جریان یکنواخت جدیدی با عمق جریان جدید خواهیم داشت. از سوی دیگر، اگر شیب کف کانال کمتر شود، برعکس این روند اتفاق می‌افتد.

شیب کف کانال را با $$\large S_0$$ نشان می‌دهیم. اگر $$\large S_0$$، سطح مقطع $$\large A_c$$ و ضریب اصطکاک سطح $$\large f$$ در جریان کانال باز، ثابت بماند و افت هد با میزان کاهش ارتفاع برابر باشد، جریان یکنواخت خواهد بود. همان‌طور که قبلاً در مقاله جریان در کانال باز - از صفر تا صد، نشان دادیم، افت هد به صورت زیر تعریف می‌شود.

$$\large h_L \: = \: f \times \: \frac {L} {D_h} \times \frac {V^2} {2 g}$$

از آنجایی که $$\large h_L \: = \: S_0L$$ و $$\large D_h \: = \: 4 R_h$$، رابطه بالا را می‌توانیم به شکل زیر بازنویسی کنیم.

$$\large S_0L \: = \: f \times \: \frac {L} {R_h} \times \frac {V^2_0} {8 g}$$

با حل معادله بالا برای $$\large V_0$$، سرعت یکنواخت جریان و نرخ دبی به صورت زیر محاسبه می‌شود.

$$\large V_0 \: = \: C \sqrt {S_0 R_h} \\~\\ \large \dot{V} \: = \: C A_c \sqrt{S_0 R_h}$$

دو رابطه اخیر، معادلات شزی و ضریب $$\large C \: = \: \sqrt { \frac {8g} {f} }$$ به کار رفته در آنها، ضریب شزی نامیده می‌شوند و بیانگر رفتار هیدرودینامیکی بستر جریان هستند. این ضریب برای نخستین بار توسط آنتوان شزی (Antoine de Chezy) (مهندس فرانسوی) و در سال ۱۷۶۹ میلادی برای انتقال آب به پاریس مورد استفاده قرار گرفته بود. دامنه ضریب شزی از حدود $$\large 30 \: \frac { \sqrt {m} } {s}$$ در کانال‌های کوچک (با سطح خشن) تا مقدار $$\large 90 \: \frac { \sqrt {m} } {s}$$ در کانال‌های بزرگ (با سطح نرم) تغییر می‌کند. دامنه این تغییرات را می‌توان در سیستم انگلیسی از $$\large 60 \: \frac { \sqrt {ft} } {s}$$ تا $$\large 160 \: \frac { \sqrt {ft} } {s}$$‌ در نظر گرفت.

برای به دست آوردن ضریب شزی، ابتدا باید ضریب اصطکاک f را بیابیم. ضریب اصطکاک همانند جریان داخل لوله، با کمک نمودار مودی و برای جریان کاملاً متلاطم ($$\large Re \: \rightarrow \: \infty$$) به شکل زیر به دست می‌آید.

$$\large f \: = \: [ 2.0 \: \log (14.8 \: \frac {R_h} {\epsilon} )] ^ { -2 }$$

در رابطه بالا، $$\large \epsilon$$ سختی متوسط سطح است. جریان در کانال باز در بیشتر مواقع از نوع متلاطم (Turbulent)‌ است و هنگامی که جریان به حالت یکنواخت می‌رسد، کاملاً توسعه یافته خواهد بود. در نتیجه، استفاده از رابطه ضریب اصطکاک جریان متلاطم منطقی است. همچنین از طرف دیگر، در اعداد رینولدز بالا، منحنی ضریب اصطکاک نسبت به سختی سطح، تقریباً افقی و در نتیجه مستقل از عدد رینولدز می‌شود. جریان در این ناحیه، جریان کاملاً متلاطم (Fully Rough Turbulent Flow) نامیده می‌شود.

از ابتدای معرفی معادلات شزی تاکنون، تلاش‌های گسترده‌ای برای استخراج روابط تجربی ساده‌تر برای سرعت متوسط و نرخ دبی انجام شده است. فیلیپ گاکلر (Philippe-Gaspard Gauckler) فرانسوی، در سال 1868 و رابرت مانینگ (Robert Manning) ایرلندی، در سال 1889 به صورت کاملاً مستقل از هم، ضریب شزی را به صورت رابطه زیر تعریف کردند.

$$\large C \: = \: \frac {a} {n} \: {R_h} ^ {1/6}$$

در رابطه بالا، $$\large n$$ ضریب مانینگ (Manning Coefficient) بوده و مقدار آن به سختی سطوح کانال وابسته است. به این ترتیب، معادلات سرعت یکنواخت و دبی جریان یکنواخت به شکل زیر نوشته می‌شود. این معادلات به معادلات مانینگ یا معادلات گاکلر--مانینگ معروف هستند.

$$\large V_0 \: = \: \frac {a} {n} \: {R_h} ^ {2/3} {S_0} ^ {1/2} \\~\\ \large \dot{V} \: = \: \frac {a} {n} \: A_c {R_h} ^ {2/3} {S_0} ^ {1/2}$$

ضریب $$\large a$$ در واحد $$\large SI$$ به صورت $$\large a \: = \: 1 \: \frac {m ^ {1/3} } {s}$$ و در واحد انگلیسی به صورت $$\large a \: = \: 1.486 \: \frac {ft ^ {1/3} } {s}$$ تعریف می‌شود. همان‌طور که می‌دانید، شیب کف کانال $$\large S_0$$ و ضریب مانینگ $$\large n$$، بدون بُعد هستند. حال، اگر شعاع هیدرولیکی $$\large R_h$$ برحسب متر در معادله وارد شود، سرعت و دبی در سیستم $$\large SI$$ به ترتیب برحسب $$\large m / s$$ و $$\large m ^3 / s$$ به دست می‌آیند.

جریان یکنواخت بحرانی

جریان یکنواخت عبوری از کانال، هنگامی بحرانی می‌شود که عدد فرود (Froude Number) برابر یک و سرعت جریان مساوی با سرعت موج ($$\large V_c \: = \: \sqrt {g \: y_c}$$)‌ باشد. هنگامی که نرخ دبی حجمی $$\large \dot{ V}$$، شیب کانال $$\large S_0$$ و ضریب مانینگ $$\large n$$ معلوم باشد، عمق قائم جریان ($$\large y_n$$) قابل محاسبه است. از آنجایی که $$\large A_c$$ و $$\large R_h$$ هر دو تابع $$\large y_n$$ هستند، تنها راه به دست آوردن $$\large y_n$$، سعی و خطا و روش‌های عددی است. اگر $$\large y_n \: = \: y_c$$ باشد، جریان از نوع جریان یکنواخت بحرانی است و شیب کف کانال $$\large S_0$$ با شیب بحرانی $$\large S_c$$ برابر خواهد بود. اگر به جای نرخ دبی $$\large \dot {V}$$، عمق جریان $$\large y_n$$ معلوم باشد، نرخ دبی حجمی را می‌توان با کمک معادله مانینگ و عمق جریان بحرانی به دست آورد. اکنون، شرط بحرانی بودن جریان به صورت $$\large y_n \: = \:y_c$$ بیان می‌شود.

حال می‌دانیم که در جریان یکنواخت بحرانی، رابطه‌های $$\large S_0 \: = \: S_c$$ و $$\large y_n \: = \: y_c$$ برقرارند. اکنون اگر در معادله مانینگ، به جای $$\large \dot {V }$$ و $$\large S_0$$، به ترتیب $$\large \dot { V} \: = \: A_c \: \sqrt{g \: y_c}$$ و $$\large S_c$$ را بنویسیم و معادله را برحسب $$\large S_c$$ مرتب کنیم، شیب بحرانی به شیوه زیر قابل محاسبه خواهد بود.

$$\large S_c \: = \: \frac {g \: n^2 y_ c} {a^ 2 R_h ^ { 4/3 }}$$

برای فیلم جریان یا جریان در کانالی با سطح مقطع مستطیلی و عرض زیاد که رابطه $$\large b \: \gg \: y_c$$ برقرار است، می‌توانیم رابطه اخیر را به شکل زیر بازنویسی کنیم.

$$\large S_c \: = \: \frac {g n^2} {a ^2 {y_c} ^ {1/3 } }$$

طبق این رابطه، با داشتن ضریب مانینگ $$\large n$$ و در یک کانال با مقطع مستطیلی و عرض زیاد، برای حفظ عمق جریان بحرانی در مقدار $$\large y_c$$، شیب کانال باید برابر $$\large S_c$$ باشد.

روش برهم‌نهی جریان یکنواخت در کانال‌هایی با محیط غیریکنواخت

میزان سختی سطح و درنتیجه، ضریب مانینگ برای بیشتر کانال‌های طبیعی و برخی از کانال‌های مصنوعی ساخته شده به دست انسان، در روی محیط تر شونده و حتی در طول کانال متغیر است. به عنوان مثال، رودخانه‌ای را در نظر بگیرید که کف آن در نقطه‌ای پر از سنگ و در نقطه‌ای دیگر پوشیده از شن و ماسه باشد. برای حل مسائلی از این دست، چندین راه وجود دارد.

پیدا کردن یک ضریب مانینگ مؤثر برای تمام طول کانال یا تقسیم‌بندی کانال به چند قسمت و استفاده از اصل برهم‌نهی، نمونه‌هایی از این راه حل‌ها هستند. مثلاً سطح مقطع یک کانال را می‌توان به N قسمت تقسیم کرد که هریک از این N قسمت، ضریب مانینگ و نرخ دبی حجمی مخصوص به خود را دارند. هنگام تعیین محیط هر قسمت، فقط بخش‌های تر شده در مرز آن قسمت، در نظر گرفته می‌شود. نرخ دبی کانال، با مجموع نرخ دبی‌های عبوری از تمام این قسمت‌ها برابر است. برای جا افتادن بهتر موضوع، به مثال‌های زیر توجه کنید.

مثال ۱ -- نرخ دبی جریان یکنواخت در کانال باز

سؤال: آب به صورت جریان یکنواخت و نیمه‌پر از درون کانالی با سطح مقطع دایره‌ای به قطر $$\large 2 \: m$$ عبور می‌کند. این کانال شیبی برابر $$\large 1.5 \: m / km$$ دارد. به شکل زیر توجه کنید. اگر کانال با بتن پرداخت شده، ساخته شده باشد، دبی حجمی آب را تعیین کنید. ضریب مانینگ برای کانال باز از جنس بتن پرداخت شده، برابر $$\large n \: = \: 0.012$$ است.

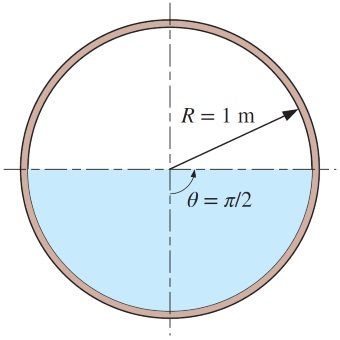
پاسخ: سطح مقطع جریان، محیط تر شونده و شعاع هیدرولیکی به ترتیب به قرار زیر است.

$$\large A_c \: = \: \frac {\pi R ^2} {2} \: = \: \frac {\pi (1 \: m) ^2 } {2} \: = \: 1.571 \: m ^2 \\~\\ \large p \: = \: \frac {2 \pi R } {2} \: = \: \frac { 2 \pi (1 \: m) } {2} \: = \: 3.142 \: m \\~\\ \large R_h \: = \: \frac {A_c} {P} \: = \: \frac {\pi R ^2 / 2} {\pi R} \: = \: \frac {R} {2} \: = \: \frac { 1 \: m} {2 } \: = \: 0.50 \: m$$

بنابراین، نرخ دبی حجمی را می‌توان با استفاده از معادله مانینگ به دست آورد.

$$\large \dot {V } \: = \: \frac {a} {n } \: A_c {R_h} ^ {2/ 3} {S_0} ^ {1/ 2} \\~\\ \large \dot{ V} \: = \: \frac {1 \: m^3 /s} {0.012} \: (1.571 \: m^2) (0.50 \: m) ^ {2/ 3} \: (1.5 / 1000) ^ {1/2} \\~\\ \large \dot{V} \: = \: 3.19 \: m^ 3 /s$$

همان‌طور که ملاحظه کردید، نرخ دبی حجمی در یک کانال، تابعی از شیب سطح زیرین کانال است. اگر با فرض ثابت ماندن تمام پارامترها، شیب کانال دو برابر شده و به مقدار $$\large 3.0 \: m / km$$ برسد، نرخ دبی حجمی جدید $$\large 4.52 \: m^3 /s$$ خواهد بود که برابر با حاصل‌ضرب نرخ دبی قبلی در عدد $$\large \sqrt {2}$$ است.

مثال ۲ -- ارتفاع کانال با مقطع مستطیلی

سؤال: آب در کانالی از جنس بتن پرداخت نشده، با عرض $$\large 4 \: ft$$ و نرخ دبی $$\large 51 \: ft ^3 /s$$ در حال انتقال است. شیب زمین طوری طراحی شده که در طول $$\large 1000 \: ft$$، به اندازه $$\large 2 \: ft$$ از ارتفاع کف کانال کاسته می‌شود. حداقل ارتفاع دیواره‌های کانال را جهت فراهم شدن شرایط برای جریان یکنواخت مطابق شکل زیر تعیین کنید. اگر کاهش ارتفاع کف کانال به اندازه $$\large 1 \: ft$$ در هر $$\large 1000 \: ft$$ از طول باشد، پاسخ چقدر خواهد بود؟ ضریب مانینگ برای کانال ساخته شده از جنس بتن پرداخت نشده، برابر $$\large n \: = \: 0.014$$ است.

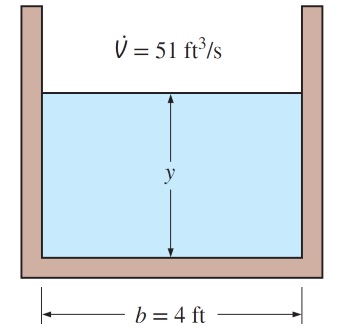
پاسخ: سطح مقطع جریان، محیط تر شونده و شعاع هیدرولیکی کانال به ترتیب زیر محاسبه می‌شوند.

$$\large A_c \: = \: b y \: = \: (4 \: ft) \times y \\~\\ \large p \: = \: b \: + \: 2 y \: = \: (4 \: ft) \: + \: 2 y \\~\\ \large R_h \: = \: \frac {A_c} {p} \: = \: \frac {4 y} {4 \: + \: 2 y}$$

شیب کف کانال برابر $$\large S_0 \: = \: 2 / 1000 \: = \: 0.002$$ است. با استفاده از معادله مانینگ، نرخ دبی آب عبوری از کانال برابر مقدار به دست آمده از رابطه زیر خواهد بود.

$$\large \dot {V} \: = \: \frac {a} {n} A_c R_h ^ { \frac {2} {3} } S_0 ^ { \frac {1} {2}} \\~\\ \large 51 \: ft^3 / s \: = \: \frac {1.486 \: ft^{\frac {1} {3}}/s} {0.014} \times (4 y \: ft ^2) \times (\frac {4 y} {4 \: + \: 2 y} \: ft) ^ {\frac {2} {3}} \times (0.002) ^ {\frac {1} {2}}$$

رابطه بالا، رابطه‌ای غیرخطی برحسب $$\large y$$ است. با کمک روش‌های عددی یا سعی و خطا می‌توان حدوداً به پاسخ $$\large y \: = \: 2.5 \: ft$$ رسید. در قسمت دوم سؤال، اگر شیب کف کانال برابر $$\large S_0 \: = \: 0.001$$ باشد، عمق جریان برابر با $$\large y \: = \: 3.3 \: ft$$ به دست می‌آید. توجه کنید که $$\large y$$ عمق جریان را نشان می‌دهد و در نتیجه، این مقدار برابر با کمترین مقدار دیواره کانال است. اما از طرف دیگر، مقدار ضریب مانینگ قطعاً با عدم قطعیت همراه است. به همین دلیل، برای طراحی و ساخت کانال، باید به این موضوع توجه لازم شود.

مثال ۳ -- کانال‌هایی با زبری غیریکنواخت

سؤال: آب در کانالی جریان دارد که شیبی برابر $$\large S_0 \: = \: 0.003$$ دارد و سطح مقطع آن در شکل زیر نشان داده شده است. ابعاد و ضرایب متفاوت مانینگ را در قسمت‌های مختلف کانال مشاهده می‌کنید. نرخ دبی حجمی آب و ضریب مانینگ مؤثر را برای کانال بیابید.

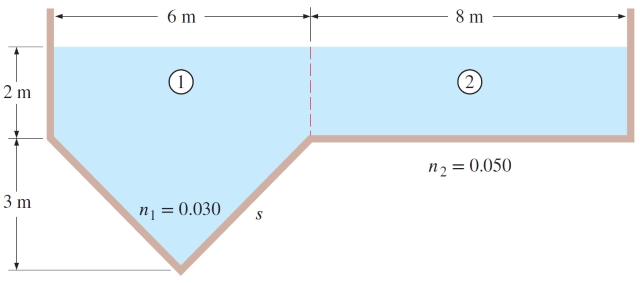
پاسخ: کانال از دو قسمت با زبری‌های متفاوت تشکیل شده است. به همین دلیل بهتر است هریک از این دو قسمت را به طور جداگانه تحلیل کنیم. ابتدا نرخ دبی را در هر قسمت با کمک معادله مانینگ به دست می‌آوریم و در نهایت با برهم‌نهی این دو قسمت، دبی کل محاسبه می‌شود. طول ضلع $$\large s$$ به راحتی و برابر $$\large s \: = \: \sqrt {3 ^2 \: + \: 3 ^2} \: = \: 4.243 \: m$$ به دست می‌آید. اکنون می‌توانیم سطح مقطع جریان، محیط تر شونده و شعاع هیدرولیکی را برای هر قسمت و سپس برای کل کانال به دست بیاوریم. ابتدا این مقادیر را برای ناحیه شماره ۱ محاسبه می‌کنیم.

$$\large A_{c1} \: = \: 21 \: m^2 ~~~~~~~~~~ p_1 \: = \: 10.486 \: m \\~\\ \large R_{h1} \: = \: \frac {A_{c1}} {p_1} \: = \: \frac {21 \: m^2} {10.486 \: m} \: = \: 2.00 m$$

حال به سراغ ناحیه شماره ۲ می‌رویم.

$$\large A_{c2} \: = \: 16 \: m^2 ~~~~~~~~~~ p_2 \: = \: 10 \: m \\~\\ \large R_{h2} \: = \: \frac {A_{c2}} {p_2} \: = \: \frac {16 \: m^2} {10 \: m} \: = \: 1.60 m$$

در نهایت، روابط قبلی را این بار، برای کل کانال می‌نویسیم.

$$\large A_{c} \: = \: 37 \: m^2 ~~~~~~~~~~ p \: = \: 20.486 \: m \\~\\ \large R_{h} \: = \: \frac {A_{c}} {p} \: = \: \frac {37 \: m^2} {20.486 \: m} \: = \: 1.806 m$$

با به کار بردن معادله مانینگ برای هر قسمت، نرخ دبی کل این جریان یکنواخت به شیوه زیر به دست می‌آید.

$$\large \dot {V} \: = \: \dot {V} _1 \: + \: \dot {V} _2 \: = \: \frac {a} {n_1} A_{c1} R_{h1} ^ { \frac {2} {3} } S_0 ^ { \frac {1}{2}} \: + \: \frac {a} {n_2} A_{c2} R_{h2} ^ { \frac {2} {3} } S_0 ^ { \frac {1}{2}} \\~\\ \large \dot {V} \: = \: (1 \: m ^ {\frac {1} {3}} /s)[\frac {(21 \: m^2) (2 \: m) ^ {\frac {2} {3}}} {0.030} \: + \: \frac {(16 \: m^2) (1.60 \: m) ^ {\frac {2} {3}}} {0.050}] (0.003) ^ {1/2} \\~\\ \large \dot {V} \: = \: 84.8 \: m ^3 /s \cong 85 \: m ^3 /s$$

اکنون با دانستن نرخ دبی کل، می‌توانیم ضریب مانینگ مؤثر را برای تمام کانال با کمک رابطه زیر محاسبه کنیم.

$$\large n_{eff} \: = \: \frac {a A_c R_h ^{\frac {2} {3}} S_0 ^ {\frac {1} {2}}} {\dot {V}} \: = \: \frac {(1 \: m ^ {\frac {1} {3}} /s) (37 \: m^2) (1.806 \: m) ^{ \frac {2} {3}} (0.003) ^{ \frac {1} {2}}} {84.8 \: m^3 /s} \: = \: 0.035$$

نکته مهمی که باید در اینجا به آن توجه کرد این است که استفاده از میانگین وزنی ضریب مانینگ، نتیجه اشتباهی به همراه دارد. ضریب مانینگ محاسبه شده با این روش برابر عبارت زیر است که اختلاف زیادی با مقدار به دست آمده برای $$\large n_{eff}$$ را نشان می‌دهد.

$$\large n_{avg} \: = \: (n_1 p_1 \: + \: n_2 p_2) / p \: = \: 0.040$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز پیشنهاد می‌شوند:

• تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد
• فلومتر (Flowmeter) – از صفر تا صد
• ورتکس (Vortex) چیست؟ — به زبان ساده
• جریان تراکم‌ پذیر (Compressible Flow) — اصول و مفاهیم

^^