جذر اعداد اعشاری | محاسبه جذر اعشاری – به زبان ساده و با مثال
جذر عملیاتی است که در ریاضی بسیار به کار برده میشود. در حل معادلات درجه دوم، هندسه و قضیه فیثاغورس و بسیاری از قضیههای دیگر ریاضی، جذر به کار میرود. در نوشتار دیگری از مجله فرادرس به بررسی جذر اعداد پرداختیم و شیوه محاسبه آن را به کمک تکنیکهای تقریبی آموختیم. در این متن از مجله فرادرس، با اعداد اعشاری سروکار خواهیم داشت و تقریبا همان روشهای پیشین را برای محاسبه جذر اعداد اعشاری به کار خواهیم گرفت که برای محاسبه جذر اعداد صحیح به کار بردیم.


اگر برای محاسبه جذر به مشکل برخوردهاید و نمیتوانید نحوه محاسبه آن را به یاد آورید پیشنهاد میکنیم که به منظور آشنایی با اعداد مربع کامل ریشه دوم و همچنین روش هندسی برای پیدا کردن جذر یک عدد، نوشتارهای اعداد رادیکالی و محاسبات مربوط به آن ها — به زبان ساده و جذر چیست ؟ — محاسبه رادیکال به زبان ساده را مطالعه کنید. همچنین خواندن مطالب معادله رادیکالی — به زبان ساده و قضیه فیثاغورس و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.
جذر اعداد اعشاری
در نوشتاری دیگر به نام جذر تقریبی اعداد به موضوع نحوه محاسبه ریشه دوم با دو رویکرد پرداختیم که طی آنها برای اعداد صحیح (مثبت) مقدار ریشه دوم را به شکلی تقریبی بدست آوردیم. در این نوشتار اما با استفاده از همان روشها، سعی داریم ریشه دوم یا جذر اعداد اعشاری را بدست آوریم. هر چند تکنیک به کار رفته درست به مانند حالت قبل است ولی تعداد عملیات و اضافه کردن ارقام به گامهای محاسباتی اندکی تفاوت دارد.
همانطور که میدانید، مبنای محاسبات تقریبی، استفاده از سعی و خطا و محاسبه به صورت تکراری است که در اینجا هم از همین روش استفاده خواهیم کرد. به این ترتیب با حدسهای اولیه و انجام بعضی از عملیات ریاضی، نزدیکترین جواب را برای محاسبه جذر اعداد اعشاری به دست خواهیم آورد.

قبل از هر چیز نیاز است که توضیحی در مورد رقم و عدد در اینجا، ارائه کنیم. در این متن هر گاه در مورد رقم یا ارقام صحبت میکنیم، منظور یکی از اعداد ۰ تا ۹ است که در جایگاههای مختلف یک عدد میتواند قرار گیرد. برای مثال در عدد ۱۴۵، رقم ۴ در جایگاه دهگان دیده میشود و آن را یک عدد نمیشناسیم. ولی هر گاه از واژه عدد استفاده میکنیم، منظورمان مجموعهای از ارقام است که یک اندازه یا مقدار را نشان میدهند. توجه داشته باشید که ارقام بدون داشتن مکان، بی معنی بوده ولی اعداد از کنار هم قرارگیری ارقام در مکانهای مختلف مانند یکان، دهگان، صدگان و هزارگان و غیره ساخته میشوند.
برای اعدادی که اعشاری هستند، پیدا کردن ریشه دوم یا جذر بسیار شبیه روشی است که برای اعداد صحیح اقدام میکنیم. تساویهای زیر را مشاهده کنید که به صورت رادیکالی نوشته شدهاند.
به همین ترتیب نیز رابطههای زیر را خواهیم داشت.
همانطور که میبینید، ابتدا عدد را بدون ارقام اعشار در نظر گرفته و ریشه دوم یا جذر آن را محاسبه میکنیم. سپس با نصف تعداد ارقام اعشار عدد اصلی، نتیجه را نمایش میدهیم. برای مثال ۰٫۰۹ اگر بدون ارقام اعشار نوشته شود، به صورت ۹ در خواهد آمد که ریشه دوم آن برابر با ۳ است. از آنجایی که ۰٫۰۹ دارای دو رقم اعشار است، ریشه دوم آن را با یک رقم اعشار یعنی به شکل ۰٫۳ نشان خواهیم داد.
نکته: همانطور که مشاهده میکنید، در این حالت باید تعداد ارقام اعشار همیشه زوج باشد. در صورتی که تعداد ارقام فرد باشند یا عدد اعشاری، ریشه صحیح نداشته باشد، روشهای تقریبی به کار خواهند آمد که در ادامه به آنها اشاره خواهیم کرد.
نحوه محاسبه جذر اعداد اعشاری
فرض کنید عددی که به جذر تقریبی یک عدد اعشاری احتیاج داریم. طبق الگویی که در مثال زیر عنوان خواهیم کرد، محاسبات را معرفی و تکنیک مورد نظر را اجرا مینمایم.
مثال ۱: ریشه دوم عدد ۹۶۰٫۱۴ چیست؟
مشخص است که ۰٫۱۴، بخش اعشاری این عدد است و ۹۶۰ نیز بخش صحیح آن است. ولی روالی و گامهایی که برای پیدا کردن ریشه تقریبی به کار خواهیم برد، با اعداد صحیح تفاوت چندانی نخواهد داشت. این کارها و گامها را در ادامه معرفی و به همراه یک مثال به کار خواهیم برد. به یاد دارید که برای جذر گرفتن، نواحی اول و دوم و سوم را به صورتی که در تصویر زیر قابل مشاهده است، تعیین کرده و محاسبات را براساس آنها انجام خواهیم داد.
نکته: البته با روشی که برای اعداد صحیح و پیدا کردن ریشه دوم یا جذر اعداد به کمک تکنیک نیوتون رافسون (جدول مقادیر) اشاره کردیم نیز میتوان برای پیدا کردن جذر تقریبی اعداد اعشاری اقدام کرد ولی در اینجا به کمک روش دستی این کار را انجام خواهیم داد.
گام اول: تفکیک دو رقم از چپ به راست
همانطور که میدانید، گام اول برای محاسبه جذر اعداد اعشاری و صحیح، جداسازی ارقام از سمت چپ است. از آنجایی که ارقام اعشار را هم باید در نظر بگیریم،
جداسازی عدد ۹۶۰٫۱۴ به صورت ۱۴، ۶۰، ۹ خواهد بود که در تصویر زیر به خوبی آن را به تصویر کشیدهایم. این ارقام را در ناحیه اول عملیات جذر ثبت میکنیم.
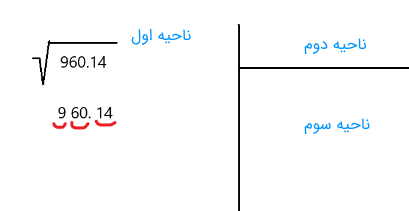
گام دوم: حدس اولیه برای رقمها تفکیک شده از سمت راست
از سمت راست ارقام برای محاسبه جذر تقریبی استفاده میکنیم. مشخص است که ۹ در سمت راست همه این ارقام حضور دارد و باید به دنبال عدد صحیحی بگردیم که مجذور یا مربع آن به ۹ نزدیکتر باشد. چون ، پس این عدد ۳ خواهد بود. پس عدد ۳ را در اولین رقم در کادر بالایی عملیات جذر قرار میدهیم. به ترتیب در نواحی جذر، مطابق با تصویر زیر، مقادیر مختلف را ثبت کرده و در مکان و ناحیهای مشخص ظاهر میسازیم. توجه داشته باشید که در ناحیه سوم مجذور ۳ یعنی رقم ۹ قرار گرفته است.
نکته: به یاد دارید که نتیجه نهایی جذر تقریبی اعداد اعشاری در ناحیه دوم قرار خواهد گرفت.

گام سوم: محاسبه تفاضل و اضافه کردن ارقام
پس از کسر کردن مجذور عدد بدست آمده از عدد اصلی، دو رقم دیگر را به پایین منتقل میکنیم. از طرفی مقدار ۳ را در ناحیه دوم در عدد ۲ ضرب میکنیم. حاصل برابر است با ۶ که مطابق با تصویر زیر، با همراه کردن یک جای خالی در کنار ۶، به دنبال عددی هستیم که بتواند با پر کردن این فضای خالی، نزدیکترین عدد به حاصل تفاضل در ناحیه اول را مشخص کند.

گام چهارم: محاسبه تفاضل و اضافه کردن ارقام
به تصویر مربوط به گام سوم دقت کنید. از آنجایی که هیچ رقمی در کنار ۶ نمیتواند قرار گیرد تا حاصل ضرب آن با عدد جدید، کوچکتر از ۶۰ باشد، صفر را در جای خالی قرار داده و یک صفر به همراه ممیز نیز در ناحیه دوم در کنار ۳ قرار میدهیم. به این ترتیب تا اینجا مقدار تقریبی جذر عدد اعشاری 960٫14، برابر با ۳۰ خواهد بود. این عملیات در تصویر زیر به خوبی قابل مشاهدهاند.
میدانید که مجذور یا توان دوم عدد ۳۰، همان ۹۰۰ است که به به ۹۶۰٫۱۴ نزدیک است.

گام پنجم: ادامه عملیات و اضافه کردن ارقام اعشار
با انتقال ارقام باقیمانده به پایین، عدد حاصل به صورت ۶۰۱۴ درآمده و لازم است که مقدار ۳۰ (مقدار تقریبی ریشه دوم در گام قبلی) را دو برابر کرده و حاصل که برابر با ۶۰ است را مشخص کنیم. این بار به دنبال رقمی میگردیم که با قرارگیری در کنار ۶۰ و ضرب آن در عدد حاصل، مقداری نزدیک به تفضل بدست آید. همانطور که در تصویر زیر میبینید، این عدد ۹ است.

پس از ضرب ۶۰۹ (با آخرین رقم برابر با ۹) در عدد ۹، حاصل ۵۴۸۱ است که با کسر کردن آن از ۵۴۸۱، مقدار ۵۳۳ بدست میآید.

رقم ۹ که در این گام مشخص شد را به عنوان ممیز در کنار ۳۰ اضافه کرده و حاصل جذر تقریبی ۹۶۰٫۱۴ تقریبا ۳۰٫۹ بدست میآید.
گام ششم: محاسبه باقیمانده و اتمام عملیات
از آنجایی که هیچ رقم دیگری باقی نمانده تا به پایین انتقال یابد و ارقام اعشار عدد اصلی به پایان رسیده است، دیگر نمیتوان عملیات را تکرار کرد و به انتهای محاسبه جذر تقریبی عدد مورد نظر رسیدهایم. برای امتحان این موضوع بهتر است ۳۰٫۹ را به صورت مربع یا به توان ۲ برسانیم.
همانطور که میبینید با مقدار واقعی عدد مورد نظر یعنی 960٫۱۴ بسیار نزدیک است. از طرفی به کمک ماشین حساب میتوانیم مقدار ریشه دوم عدد ۹۶۰٫۱۴ را بدست آورده که مقدار تقریبی 30٫9861 خواهد بود. مشخص است که نتیجه محاسبات ما برای پیدا کردن ریشه اعداد اعشاری به خوبی صورت گرفته و به پاسخی نزدیک به مقدار اصلی رسیدهایم.
نکته: در مثالی که مورد بررسی قرار گرفت، تعداد ارقام اعشار زوج بود. یعنی دو رقم اعشار در اختیارمان قرار داشت. اگر تعداد ارقام اعشار برای عددی که میخواهید ریشه یا جذر آن را محاسبه کنید، فرد باشد، یک صفر به بعد از ارقام ممیز اضافه کنید تا ارقام به صورت زوج درآید. به این ترتیب همان روالی که در قبل به آن اشاره کردیم، قابل استفاده خواهد بود.
در مثال بعدی به بررسی ریشه دوم عدد دیگری خواهیم پرداخت تا مراحل بهتر درک شود.
مثال 2: ریشه دوم یا رادیکال ۶٫۴۵ را محاسبه کنید.
باید ریشه دوم عدد 6٫۴۵ را بدست آوریم. از آنجایی که دو رقم اعشار برای این عدد وجود دارد، تفکیک آنها از راست به چپ به سادگی صورت گرفته و به شکل ۴۵ ۶ خواهد بود.
در تصویر زیر همه مراحل را برای پیدا کردن ریشه دوم عدد ۶٫۴۵ طی کردهایم. ولی برای درک بهتر، مراحل کار را به طور خلاصه تکرار خواهیم کرد.

هر مرحله را با رنگ متمایزی نمایش دادهایم. در گام اول، با توجه به جداسازی ارقام به شکل دو رقم به دو رقم، رقم ۶ حاصل میشود که نزدیک ترین عدد مربع کامل به آن، ۴ است که ریشه دوم آن برابر با ۲ است. ۲ را در ناحیه دوم جذر قرار میدهیم و تفاضل ۴ را از ۶٫۴۵ بدست میآوریم.
نکته: همانطور که دیده میشود، در همه مراحل، بدون در نظر گرفتن ممیز، محاسبه ریشه دوم اعداد اعشاری را طی میکنیم ولی هر جا که اعداد بعد از علامت اعشار را در محاسبات به کار میبریم، در عدد مربوط به نتیجه جذر، علامت ممیز را لحاظ میکنیم. دقت داشته باشید که در ناحیه اول و سوم، از ممیز استفاده نخواهیم کرد.

مثال ۳: ریشه دوم عدد 1۶٫۴ را بدست آورید.
همانطور که میبینید، این عدد یک رقم اعشار دارد و باید به تعدادی که لازم است، به طرف راست آن صفر اضافه کنیم تا تعداد ارقام اعشار زوج شود. به این ترتیب با اضافه کردن یک رقم صفر در سمت راست، به کارگیری گامهای قبلی میسر میشود.

باز هم در هر مرحله، از رنگهای جداگانه استفاده کردهایم و محاسبات را تا سه رقم اعشار ادامه دادهایم. در گام آخر به علت اینکه تعداد ارقام ممیز با دقت مورد نیاز بدست آمده (مثلا سه رقم اعشار) دیگر عملیات را تکرار نکردهایم. اگر به کمک ماشین حساب، ریشه دوم یا جذر 16٫۴ را محاسبه کنید به مقدار 4٫049691346 خواهید رسید.
میبینید که تا سه رقم اعشار عدد به دست آمده، با مقدار ماشین حساب، مطابقت دارد. در صورتی که به تعداد ارقام بیشتری برای محاسبه جذر عدد به کمک روش دستی احتیاج دارید، باید مراحل را ادامه داده و هر وقت ارقامی برای ادامه وجود نداشت، دو رقم صفر به انتهای عدد اضافه کرده و عملیات را پی میگیریم.
نکته: به یاد داشته باشید که چون این محاسبات (به جز برای اعداد مربع کامل) هیچگاه پایان نمییابد، این شیوه را محاسبه تقریبی دستی مینامیم. فقط اعداد مربع کامل هستند که در هنگام اجرای این مراحل به باقیمانده تفریق صفر رسیده و دیگر احتیاجی به تکرار مراحل نیست.
در نوشتار دیگری از مجله فرادرس به نام جذر تقریبی و روش محاسبه آن — آموزش به زبان ساده و با مثال به مسئله محاسبه تقریبی برای ریشه دوم اعداد صحیح اشاره کردیم. در آنجا نیز مثالهایی برای این کار ارائه شده که میتوانید برای توضیحات بیشتر به مطالعه آن بپردازید.
خلاصه و جمعبندی
در این متن به بررسی مراحل محاسبه جذر اعداد اعشاری به کمک روش دستی و محاسبات گام به گام پرداختیم و به کمک مثالی، راهکار ارائه شده را آموزش دادیم. همانطور که خواندید، با تکرار مراحل گفته شده، میتوان به دقت بیشتری در نتیجه حاصل رسید. به همین جهت اغلب برای پیدا کردن ریشه دوم یا جذر اعداد اعشاری با ارقام زیاد، احتیاج به ماشین حساب یا نرمافزارهای محاسباتی داریم تا با سرعت مراحل و عملیات را انجام داده و مقدار مورد نظر برای جذر اعداد اعشاری را پیدا کنیم.













سلام یه سوال داشتم
اگر عدد اعشاری باشد هر چقدر فورجه بزرگتر باشد عدد بزرگتر یا کوچک تر میشود؟
و اگر عدد منفی باشد هر چقدر فورجه بزرگتر باشد عدد بزرگتر یا کوچکتر میشود؟