توزیع های پیوسته آماری و رابطه بین آنها — به زبان ساده

یکی از روش‌های توضیح رفتار پدیده‌های تصادفی استفاده از تابع توزیع احتمال است. معمولا (و البته نه همیشه) یک پدیده تصادفی را می‌توان بوسیله تابع توزیع احتمال آن مشخص کرد. متغیرهای تصادفی یک راه و روش برای شناسایی تابع توزیع احتمال محسوب می‌شوند. در این نوشتار به بررسی توزیع های پیوسته آماری و رابطه بین آن‌ها می‌پردازیم. مطابق با دیگر نوشتارهای فرادرس در مورد متغیر تصادفی، می‌دانیم که اگر مجموعه مقادیر یک متغیر تصادفی منطبق با زیرمجموعه‌ای از اعداد حقیقی باشد، متغیر تصادفی را «پیوسته» (Continuous Random Variable) می‌نامیم. در حقیقت اگر مقادیر یک متغیر تصادفی، تشکیل یک مجموعه نامتناهی ناشمار را بدهد، آن را پیوسته می‌گوییم. بسیاری از توزیع‌های مربوط به متغیرهای تصادفی پیوسته از توزیع نرمال گرفته شده‌اند. برای مثال می‌دانیم که مجموع مربعات متغیرهای تصادفی با توزیع نرمال استاندارد تشکیل یک متغیر تصادفی کای ۲ را می‌دهد. البته می‌توان بعضی دیگر را هم براساس تعمیم روی توزیع‌های گسسته ایجاد کرد. در بخش اول از این نوشتار به روابط بین متغیرهای تصادفی گسسته اشاره شده است.

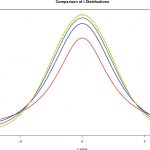
قضیه حد مرکزی (Central Limit Theorem) ارتباط بیشتر توزیع‌ها را با توزیع نرمال به صورت حدی یا مجانبی، بیان می‌کند. در دیگر نوشتارهای فرادرس با بسیاری از توابع توزیع آماری آشنا شده‌ایم. برای مشاهده لیستی از این گونه توابع می‌توانید به نوشتار توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس مراجعه کنید. همچنین خواندن مطلب امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیست.

توزیع های پیوسته آماری و رابطه بین آنها

اغلب برای توضیح رفتار پدیده‌هایی که با مقادیر کمّی (قابل اندازه‌گیری) حاصل می‌شوند از متغیرهای تصادفی پیوسته استفاده می‌کنیم. برای مثال توزیع نرمال، توزیع کوشی و توزیع فیشر کاربردهای زیادی در تحلیل داده‌های کمی دارند بطوری که بیان و توصیف بسیاری از پدیده‌های تصادفی به کمک این توزیع‌ها میسر است. برای تحلیل و شناخت داده‌هایی که از این توزیع‌ها پیروی می کنند، ابزارهای مختلفی در زبان‌های برنامه‌نویسی R و البته پایتون و کتابخانه scikit-learn وجود دارد. در این نوشتار به بررسی و معرفی بعضی از توابع که بخصوص در علم داده کاربرد بیشتری دارند پرداخته و رابطه یا نحوه تبدیل یکی به دیگری را مشخص خواهیم کرد. به منظور نمایش جامع ارتباطات بین توزیع‌های گسسته پیوسته نیز در انتها از یک تصویر که بصورت یک نمودار رابطه‌ها را نشان می‌دهد، استفاده کرده‌ایم.

فیلم آموزش شبیه سازی پیشامدهای گسسته با ارنا Arena در فرادرس

کلیک کنید

هر توزیع آماری به کمک «تابع چگالی احتمال» (Probability Density Function) یا «تابع توزیع تجمعی» (Cumulative Probability Function) آن مشخص شده و معرفی می‌شود. البته در بعضی از موارد ممکن است دسترسی به تابع چگالی احتمال میسر نباشد. در این حالت تابع مشخصه (Characteristic Function) یک روش برای معرفی منحصر بفرد توزیع متغیر تصادفی محسوب می‌شود. به تابع چگالی احتمال به اختصار PDF و به تابع توزیع تجمعی احتمال نیز CDF‌ گفته می‌شود. در ادامه به معرفی بعضی از «متغیرهای تصادفی» (Random Variable) و توزیع‌های معروفشان می‌پردازیم. اگر مجموعه مقادیر متغیر تصادفی $$X$$ زیرمجموعه‌ای از اعداد حقیقی یا به صورت یک مجموعه نامتناهی شمارش‌ناپذیر باشد، آن متغیر تصادفی را پیوسته می‌نامند. در این نوشتار به بررسی و معرفی ارتباط بین متغیرهای تصادفی پیوسته و توزیع‌هایشان خواهیم پرداخت. برای آشنایی با توزیع‌های گسسته و نحوه ارتباط آن‌ها با یکدیگر بهتر است قسمت اول این نوشتار با عنوان توزیع های گسسته آماری و رابطه بین آن‌ها --- به زبان ساده را مطالعه کنید.

توزیع یکنواخت

اگر جرم احتمال برای متغیر تصادفی $$X$$ در همه ناحیه تکیه‌گاه متغیر تصادفی $$X$$ به شکل یکسان توزیع شده باشد، متغیر تصادفی $$X$$ را با توزیع یکنواخت می‌شناسند. این توزیع حول مرکز بازه مربوط به تکیه‌گاه،‌ متقارن بوده و در نتیجه چولگی ندارد. یکی از کاربردهای مهم متغیر تصادفی با توزیع یکنواخت، این است که تابع توزیع تجمعی یا CDF هر توزیع احتمالی، از این توزیع پیروی می‌کند. در این صورت خواهیم داشت:

$$\large F_X(x) \sim U(0,1)$$

این امر در شبیه‌سازی داده‌های تصادفی برای هر توزیعی براساس توزیع یکنواخت، بسیار اهمیت دارد. در بیشتر نرم‌افزارهای رایانه‌ای به منظور تولید اعداد تصادفی از توزیع‌های مختلف، ابتدا یک عدد تصادفی از توزیع یکنواخت تولید شده سپس با استفاده از تبدیل عکس تابع توزیع، آن را به مقدار تصادفی از توزیع مورد نظر مبدل می‌کنند.

توزیع نرمال، لوگ نرمال، Student's t و کای ۲

یکی از مهم‌ترین توزیع‌های آماری، توزیع نرمال (Normal Distribution) است. البته این توزیع گاهی «توزیع گاوسی» (Gaussian Distribution) یا توزیع «گاوس-لاپلاس» (Laplace-Gauss) نیز نامیده می‌شود. از آنجایی که این توزیع دارای منحنی به شکل زنگ است، گاهی به آن «منحنی زنگی شکل» (Bell Curve) نیز می‌گویند. بیشتر پدیده‌های تصادفی با مقدارهای کمّی از این توزیع پیروی می‌کنند. یا به کمک «قضیه حد مرکزی» (Central Limit Theorem)  بطور مجانبی به این توزیع مرتبط می‌شوند. بنابراین توزیع نرمال اهمیت زیادی در آمار و تحلیل داده‌های آماری دارد.

فیلم آموزش تجزیه و تحلیل آماری با نرم افزار StatPlus در فرادرس

کلیک کنید

در تصویر زیر منحنی تابع چگالی احتمال (pdf) توزیع نرمال دو متغیره را مشاهده می‌کنید.

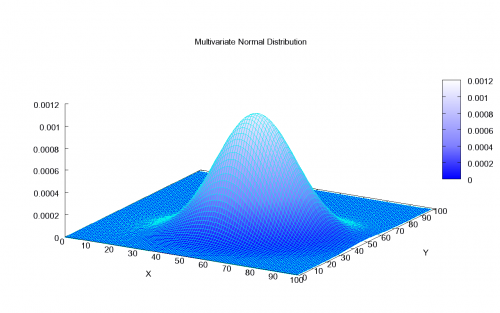
پارامترهای چگالی احتمال برای توزیع نرمال، «میانگین» ($$\mu$$) و «انحراف استاندارد» ($$\sigma$$) هستند و فرم چگالی به صورت زیر نوشته می‌شود. برای چنین متغیر تصادفی می‌نویسیم $$X\sim N(\mu,\sigma^2)$$ و می‌خوانیم $$X$$ دارای توزیع نرمال با پارامترهای $$\mu$$ و $$\sigma^2$$ است.

$$\large {\displaystyle f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}$$

اگر میانگین توزیع نرمال برابر با صفر و واریانس آن نیز مقدار واحد (یک) باشد، توزیع را «نرمال استاندارد» (Standard Normal) می‌نامند. در این صورت تابع چگالی آن به شکل زیر درخواهد آمد. معمولا چنین متغیر تصادفی را با نام $$Z$$ می‌شناسند.

$$\large {\displaystyle f(z)={\frac {1}{\sqrt {2\pi}}}e^{-{\frac {z^{2}}{2}}}}$$

با استفاده از رابطه زیر می‌توانیم هر متغیر تصادفی مثل $$X$$ با توزیع نرمال با میانگین $$\mu$$ و واریانس $$\sigma^2$$ را به توزیع نرمال استاندارد تبدیل کنیم.

$$\large {\displaystyle Z={\dfrac {X-\mu}{\sigma}}}$$

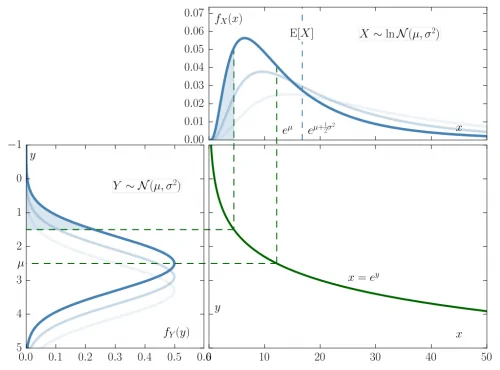
از طرفی توزیع لوگ نرمال (Log-Normal Distribution) نیز می‌تواند مربوط به متغیر تصادفی باشد که لگاریتم آن دارای توزیع نرمال است. به عنوان تعریف متغیر تصادفی با توزیع لوگ نرمال می‌توان گفت که اگر یک متغیر تصادفی مانند $$X$$‌ دارای توزیع لوگ نرمال با پارامترهای $$\mu$$ و $$\sigma^2$$ باشد، آنگاه توزیع $$\ln(X)\sim N(\mu,\sigma^2)$$، نرمال خواهد بود. تصویر زیر رابطه و نحوه تبدیل یک متغیر تصادفی با توزیع نرمال به لوگ نرمال و برعکس را نشان می‌دهد. واضح است که توزیع لوگ نرمال دارای چولگی به سمت راست است. از طرفی مشخص است که مقادیر یا تکیه‌گاه این متغیر تصادفی در بازه اعداد مثبت $$(0,+\infty)$$ قرار می‌گیرد.

توزیع student's t یا همان توزیع T نیز از حالتی براساس توزیع نرمال استاندارد تولید می‌شود. اگر به جای استفاده از میانگین و واریانس در تبدیل متغیر تصادفی نرمال به نرمال استاندارد، از برآوردهای آن‌ها یعنی میانگین نمونه‌ای و واریانس نمونه‌ای استفاده کنیم، متغیر تصادفی تبدیل شده، دارای توزیع T خواهد بود. به همین دلیل، توزیع T را در گروه «توزیع‌های نمونه‌ای» (Sampling Distribution) قرار می‌دهند. به این ترتیب متغیر تصادفی $$T$$ به صورت زیر تعریف می‌شود.

$$\large T=\dfrac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1)$$

واضح است که $$\overline{X}$$ و $$S$$ از طریق یک نمونه تصادفی $$n$$ تایی از جامعه آماری با توزیع نرمال پدید آمده‌اند و داریم:

$$\large \overline{X}=1/n\sum_{i=1}^nX_i$$

$$\large S^2=\dfrac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2$$

پارامتر اصلی برای این توزیع $$n-1$$ است که درجه آزادی نامیده می‌شود. شکل تابع چگالی احتمال (PDF) این متغیر تصادفی درست به مانند توزیع نرمال، متقارن و زنگی شکل است ولی دم‌های آن دارای احتمال بیشتری نسبت به توزیع نرمال هستند.

به عنوان یک توزیع دیگر که از توزیع نرمال منشاء‌ می‌گیرد، می‌توان به توزیع کای ۲ یا کای مربع (Chi Square) اشاره کرد. اگر $$n$$‌ متغیر تصادفی با توزیع نرمال استاندارد را به توان ۲ برسانیم و با یکدیگر جمع کنیم، یک متغیر تصادفی با توزیع کای ۲ خواهیم داشت. پارامتر اصلی برای این توزیع، $$n$$‌ است که به مانند توزیع T، درجه آزادی نامیده می‌شود. واضح است که در اینجا $$n$$ تعداد متغیرهای توزیع نرمال استاندارد است که مجموع مربعاتشان محاسبه شده است. همانطور که مشاهده شد، توزیع نرمال، توزیع اصلی برای توزیع‌های لوگ نرمال، T و کای ۲ محسوب می‌شود.

توزیع وایبل و نمایی

متغیر تصادفی «وایبل» (Weibull) یک متغیر تصادفی با مقادیر پیوسته است. تکیه‌گاه این متغیر تصادفی، اعداد حقیقی نامنفی است در نتیجه در مواردی که متغیر تصادفی مربوط به طول عمر باشد، می‌توان از این توزیع استفاده کرد. از این متغیر تصادفی و توزیع آن بخصوص در مباحث مربوط به قابلیت اطمینان و حتی پیش‌بینی آب و هوا استفاده می‌شود. متغیر تصادفی وایبل با متغیر تصادفی با توزیع یکنواخت پیوسته براساس رابطه زیر مرتبط است. بنابراین اگر $$E$$ یک متغیر تصادفی با توزیع وایبل با پارامترهای $$\lambda$$ و $$k$$ باشد خواهیم داشت:

$$\large W=[-\ln(U)]^{\frac{1}{k}}\lambda$$

که در آن $$U$$‌ دارای توزیع یکنواخت در بازه $$(0,1)$$ است.

در مورد توزیع نمایی، شاید بتوان ارتباط جالبی بین یک متغیر تصادفی گسسته با متغیر تصادفی پیوسته جستجو نمود. در یک آزمایش تصادفی پواسن، تعداد رخداد (موفقیت یا شکست) در واحد زمان یا مکان، مورد نظر بود. ولی اگر متغیر تصادفی را زمان رسیدن به اولین رخداد (موفقیت یا شکست) در نظر بگیریم، یک متغیر تصادفی پیوسته ایجاد شده که دارای «توزیع نمایی» (Exponential Distribution) است. برای مثال می‌توانیم زمان انتظار تا ورود مشتری بعدی در یک فروشگاه را با توزیع نمایی بیان کنیم. به یاد دارید که تعداد مشتریان از توزیع پواسن پیروی می‌کرد. از طرفی می‌توان در توزیع هندسی، به جای تکرارهای آزمایش برای رسیدن به اولین موفقیت زمان رسیدن به kosjdk موفقیت را در نظر گرفت که به این ترتیب متغیر تصادفی جدیدی با توزیع نمایی تولید می‌شود.

همانطور که گفته شد، توزیع وایبل نیز برای نمایش زمان یا طول عمر به کار می‌رود. از این جهت توزیع‌های نمایی و وایبل هر دو در زمینه، توصیف طول عمر پدیده‌های تصادفی کاربرد دارند. ولی باید توجه داشت که در توزیع نمایی، نرخ خرابی یا متوسط طول عمر، ثابت است در حالیکه در توزیع وایبل نرخ خرابی یا متوسط طول عمر، تابعی نزولی یا صعودی محسوب می‌شود.

توزیع گاما و بتا

توزیع گاما (Gamma Distribution) یک توزیع آماری دو پارامتری است. از آنجا که توزیع نمایی و کای-2 حالت خاصی از توزیع گاما محسوب می‌شوند، این توزیع اهمیت ویژه‌ای دارد. تکیه‌گاه‌‌ این توزیع، مجموعه مقادیر مثبت است. البته چولگی زیاد این توزیع برای توصیف پدیده‌هایی که تابع احتمال آن‌ها به مقادیر بزرگتر تمایل زیادی دارند مناسب است. اغلب از این توزیع برای نمایش توزیع متغیرهای تصادفی مرتبط با «زمان انتظار» (Waiting Time) استفاده می‌شود. اگر توزیع گاما را با پارامتر شکل با مقدار واحد در نظر بگیریم، یک توزیع نمایی خواهیم داشت. به این معنی که اگر شکل تابع توزیع گاما را ثابت در نظر بگیریم، تبدیل به توزیع نمایی خواهد شد.

فیلم آموزش مسائل تشریحی توزیع های گسسته و پیوسته در آمار و احتمال (رایگان) در فرادرس

کلیک کنید

توزیع بتا (Beta Distribution) نیز در بسیاری از موارد در استنباط بیزی به عنوان توزیع پیشین پارامتر $$p$$ در توزیع دوجمله‌ای به کار  می‌رود. به این ترتیب، ارتباطی بین توزیع دو جمله‌ای و توزیع بتا بوجود می‌آید. ذکر این نکته نیز ضروری است که اگر $$X$$ و $$Y$$ دو متغیر تصادفی با توزیع گاما باشند، نسبت یکی به مجموعشان، دارای توزیع بتا خواهد بود. پس بین توزیع گاما و توزیع بتا نیز ارتباطی برقرار است.

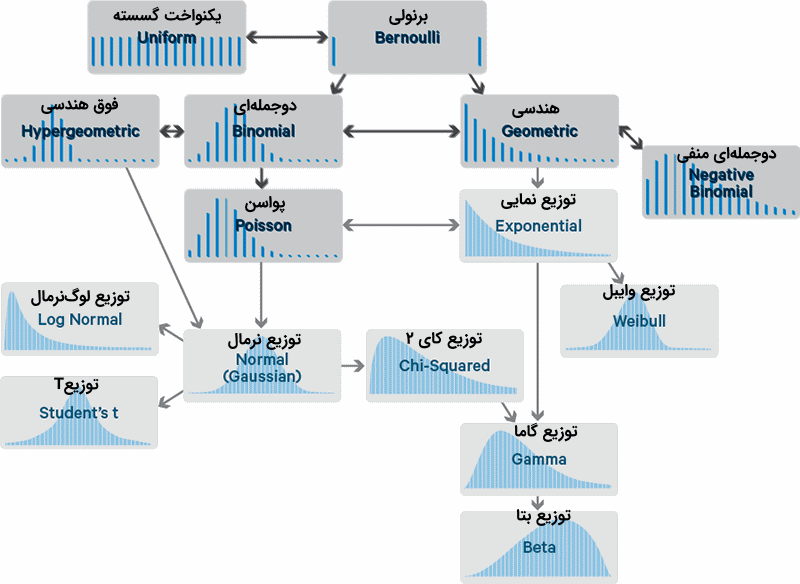
نمودار ارتباطی بین توزیع‌های گسسته و پیوسته

در تصویر زیر ارتباط بین توزیع‌های گسسته و پیوسته دیده می‌شوند. این نمودار به خوبی ارتباط بین توزیع‌های پیوسته را نیز بیان می‌کند. همانطور که گفته شد، توزیع نمایی می‌تواند براساس توزیع پواسن یا توزیع هندسی نمایش داده شود. از طرفی ارتباط بین توزیع نرمال، لوگ نرمال و کای۲ و توزیع T در نمودار دیده می‌شود. به وضوح نقش اصلی متغیر تصادفی نرمال در تولید متغیرهای تصادفی با توزیع لوگ‌نرمال و کای ۲ و همچنین T قابل مشاهده است. همچنین می‌توان توزیع پواسن را منشاء توزیع نمایی و به تبع آن توزیع گاما، وایبل، گاما و بتا در نظر گرفت.

نکته: کادر مربوط به توزیع‌های گسسته در این تصویر کمی تیره‌تر از توزیع‌های پیوسته دیده می‌شوند. خطوط ترسیمی بین توزیع‌ها، نحوه ارتباط را نشان می‌دهد که ممکن است یکطرفه یا دو طرفه باشد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• مجموعه آموزش‌های SPSS
• آموزش آمار و احتمال مهندسی
• آزمایش تصادفی، پیشامد و تابع احتمال
• جامعه آماری — انواع داده و مقیاس‌های آن‌ها
•  تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
• توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس

^^