توربین پلتون (Pelton Wheel) – از صفر تا صد

قبلاً در مجله فرادرس، توربین فرانسیس را به عنوان نمونهای پرکاربرد از توربینهای عکسالعملی معرفی کردیم. در مقاله حاضر، به سراغ یک توربین ضربهای محبوب آمدهایم. توربین پلتون تنها توربین هیدرولیکی از نوع ضربهایست که هم اکنون نیز مورد استفاده قرار میگیرد. این توربین به طور ویژه برای هد (head) زیاد طراحی شده است. روتور این توربین از دیسکی تشکیل شده که تعدادی پره دور تا دور آن نصب شدهاند. به این پرهها، بشقابک (bucket) هم گفته میشود. یک یا چند نازل، طوری قرار گرفتهاند که جت آب خروجی از هر نازل بتواند به صورت مستقیم و مماس به دیسک، به سمت مرکز هر یک از بشقابکها پرتاب شود. یک جداکننده یا اسپلیتر (splitter) وظیفه دارد جت ورودی به هر بشقابک را به دو جریان مساوی تقسیم کند. این دو جریان مساوی، پس از عبور از یک مسیر منحنی در سطح داخلی بشقابک، در راستایی مخالف راستای جت ورودی، بشقابک را ترک میکنند. شماتیک تولید برق با استفاده از توربین پلتون را در تصویر متحرک زیر مشاهده میکنید.

تاریخچه توربین پلتون
«لستر آلن پلتون» (Lester Alan Pelton) مخترع آمریکایی، در سال 1860 میلادی و در حالی که سی سال سن داشت، به دنبال یافتن گنج، به غرب آمریکا سفر کرد و در معدنی در شمال کالیفرنیا مشغول به کار شد. در آن زمان، بیشتر کارها با کمک توان حاصل از موتورهای بخار انجام میشد. اما این موتورها حجم بسیار زیادی چوب را به عنوان سوخت مصرف میکردند. چرخهای آبی که در رودخانههای بزرگ با راندمان بسیار پایین مورد استفاده قرار میگرفتند، در رودخانههای کوچک نزدیک معدن، بیمصرف بودند. از این رو، پلتون شروع به طراحی چرخی کرد که بتواند در مقادیر دبی آبی کم هم کار کند.
در اواسط دهه 1870، او اولین نمونه آزمایشگاهی توربینش را از جنس چوب ساخت و اولین نمونه واقعی آهنی نیز در سال 1878 در معدنی در نزدیکی شهر نوادا نصب شد. مزیتهای مثبت و راندمان بالای چرخ آبی پلتون باعث شد اختراع او به زودی به تولید انبوه برسد. به طوری که تا سال 1900، بیش از ۱۱۰۰۰ توربین پلتون در سرتاسر جهان مورد بهرهبرداری قرار گرفته بود. عکسی واقعی از ثبت اختراع پلتون در سال ۱8۸۰ در شکل زیر، نشان داده شده است. ابتکار پلتون، طراحی جدا کنندهای بود که جت ورودی را به دو جریان مساوی تقسیم کند. همین ایده باعث شد راندمان چرخهای آبی از حدود 35٪ به 90٪ افزایش پیدا کند.
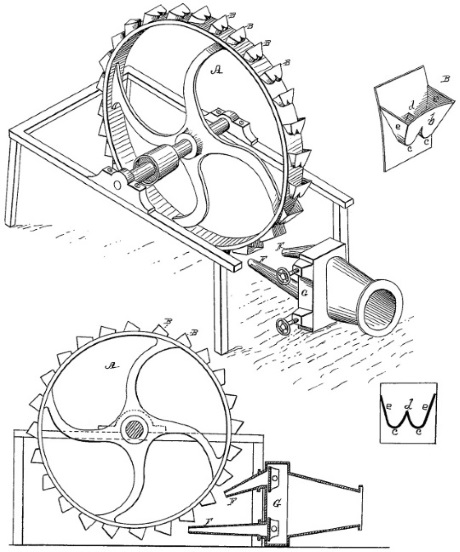
بخشهای توربین پلتون
توربینهای ضربهای انواع بسیار گوناگونی دارند. ولی مدلی که پلتون اختراع کرد، هنوز هم بیشترین راندمان را داراست. شکل زیر، قسمتهای مختلف توربین پلتون را نشان میدهد. در این بخش، برخی از قسمتهای اصلی این توربین را بررسی میکنیم.
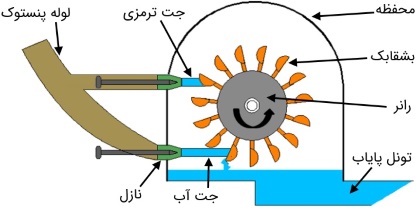
نازل
آب از بالادست جریان، با عبور از یک لوله تحت فشار به نام پنستوک (penstock)، به نازل میرسد. با استفاده از این نازل، جت آب با سرعت بالا به بشقابکها برخورد میکند. با کمک یک میله سوزنی شکل که داخل نازل قرار دارد، میتوان جت آب و قطع و وصل شدن آن را کنترل کرد. این میله فقط در راستای طولی و به جلو و عقب حرکت میکند.
رانر و بشقابک
رانر توربین پلتون از یک دیسک تشکیل شده که تعدادی بشقابک روی محیط آن قرار گرفتهاند. بشقابک و جداکننده آن طوری طراحی شدهاند تا جت خروجی آب، زاویه 160 یا 170 درجه داشته باشد. جنس بشقابکها میتواند از چدن، آلیاژ برنز و فولاد و فولاد ضد زنگ باشد. انتخاب جنس توربین، به هد ورودی آب و تأثیر آن روی خوردگی بدنه بستگی دارد. بشقابکها پس از دریافت جت آب، به حرکت درمیآیند و رانر را میچرخانند. با چرخش رانر، محور (shaft) خروجی هم شروع به چرخش میکند.
محفظه
برای اینکه آب برگشتی (جت خروجی از بشقابکها) به اطراف پاشیده نشود و تمام آب در تونل پایاب (tail race) تخلیه شود، از یک محفظه استفاده شده است. محفظه توربین پلتون، کاربرد هیدرولیکی ندارد.
جت ترمزی
اگر مسیر خروجی نازل کاملاً مسدود شود، حجم آبی که به بشقابکهای رانر برخورد میکند، به صفر خواهد رسید. ولی رانر به دلیل داشتن اینرسی زیاد، تا مدتی طولانی به چرخش خود ادامه خواهد داد. در این وضعیت و برای اینکه در فاصله زمانی کوتاهی، توربین متوقف شود، از یک نازل کوچک استفاده میشود تا آب را به پشت بشقابکها پرتاب کند. این جت آب، به عنوان جت ترمزی شناخته میشود.
عملکرد توربین پلتون
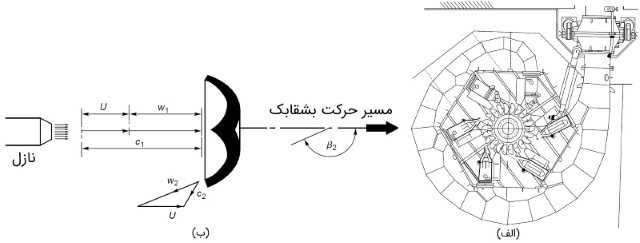
شکل زیر (الف)، یک توربین پلتون با محور عمودی و شش نازل را نشان میدهد. حال، جت خروجی یکی از این نازلها را در نظر بگیرید که به سمت یکی از بشقابکها پرتاب میشود. مثلث سرعت برای این جت نیز، در شکل زیر (ب) نمایش داده شده است.
سرعت جت را در ورودی با $$\large c_1$$ و سرعت بشقابک را با $$\large U$$ نشان دادهایم. بنابراین، سرعت نسبی برابر با $$\large w_1 = c_1 - U$$ است. در خروجی بشقابک هم مثلث سرعت را برای نیمی از جریان رسم کردهایم. سرعت نسبی $$\large w_2$$ و زاویه بین جریان خروجی و جهت جریان اولیه $$\large \beta_2$$ است. با کمک نمودار سرعت، سرعت خروجی $$\large c_2$$ را میتوان به دست آورد.
با یادآوری معادله توربین اویلر، کار مخصوص انجام شده توسط آب به صورت زیر است.
$$\large \Delta W = U_1 c_{\theta 1} \: - U_2 c_{\theta 2}$$
با توجه به ماهیت عملکرد توربین پلتون، روابط $$\large U_1 = U_2 = U$$ و $$\large c_{\theta 1} = c_1$$ نیز مفروض است. مؤلفه $$\large c_{\theta 1}$$، سرعت را در جهت مماسی نشان میدهد. در نتیجه، رابطه کار مخصوص به شکل زیر بازنویسی میشود.
$$\large \Delta W = U[U + w_1 - (U + w_2 \cos \beta _2)] = U(w_1 - w_2 \cos \beta_2)$$
همانطور که در شکل قبل دیدیم، رابطه $$\large c_{\theta 2} < 0$$ برقرار است. در نتیجه، سرعت جت برگشتی آب در جهت مماسی با کمک رابطه زیر محاسبه میشود.
$$\large c_{\theta 2} = U + w_2 \cos \beta _2$$
اثر اصطکاک روی جریان سیال در داخل بشقابک، باعث میشود سرعت خروجی از سرعت ورودی کمتر باشد. با اضافه کردن $$\large w_2 = k w_1$$ و با شرط $$\large k < 1$$ میتوانیم رابطه قبل را به شکلی دیگر بنویسیم.
$$\large \Delta W = Uw_1(1 - k \cos \beta_2) = U(c_1-U)(1 - k \cos \beta_2)$$
(رابطه ۱)
حال میتوانیم راندمان $$\large \eta _ R$$ را به صورت نسبت کار مخصوص انجام شده به انرژی جنبشی ورودی و به صورت زیر تعریف کنیم.
$$\large \eta _ R = \frac {\Delta W} {\frac {1} {2} c^2_1} = \frac {2U(c_1 - U)(1-k \cos \beta_2)} {c^2_1}$$
(رابطه ۲)
با سادهسازی رابطه بالا، راندمان را میتوان برابر با عبارت زیر نوشت.
$$\large \eta _ R = 2v(1-v)(1 - k\cos \beta_2)$$
(رابطه ۳)
در اینجا، نسبت سرعت بشقابک به سرعت جت ورودی با $$\large v$$ نشان داده شده است. برای یافتن راندمان بهینه، باید از رابطه قبل برحسب $$\large v$$ مشتقگیری انجام دهیم.
$$\large \frac{\text{d}{\eta _R}}{\text{d}v} = 2 \frac {d} {dv} (v - v^2)(1 - k \cos \beta _2) = 2(1 - 2v)(1 - k \cos \beta_2) = 0$$
در نتیجه، بالاترین راندمان رانر، در نسبت $$\large v = 0.5$$ رخ میدهد. یعنی $$\large U = \frac {c_1} {2}$$ باید برقرار باشد. با جایگذاری این مقدار در رابطه راندمان، راندمان ماکسیمم، برابر مقدار زیر است.
$$\large \eta _{R \:\: max} = 1 - k \cos \beta_2$$
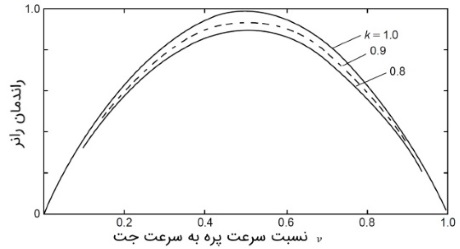
تغییرات راندمان رانر با نسبت سرعت پرهها، در شکل زیر نمایش داده شده است. در این نمودارها، مقدار $$\large k$$ برابر سه عدد $$\large 0.8$$، $$\large 0.9$$ و $$\large 1.0$$ فرض شده و زاویه $$\large \beta _ 2$$ مساوی $$\large 165$$ درجه است. در کاربردهای واقعی، مقدار $$\large k$$ معمولاً بین $$\large 0.8$$ و $$\large 0.9$$ طراحی میشود.
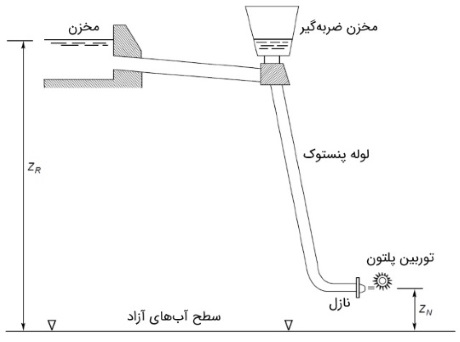
شماتیک هیدروالکتریکی توربین پلتون را در شکل زیر ملاحظه میکنید. آب از طریق لوله پنستوک به نازل رسیده و سپس با جت سریع به سمت رانر پرتاب میشود. برای کم کردن آثار مخرب سرج (surge)، از یک مخزن ضربهگیر استفاده میشود که در نزدیکی هد لوله پنستوک قرار گرفته و به مسیر جریان چسبیده است. این مخزن قادر است ضربههای گذرا را دفع کند. با توجه به شکل، میتوانیم هد مجموع را به صورت $$\large H_G = z_R - z_N$$ بنویسیم. مقادیر ارتفاع، نسبت به سطح آبهای آزاد نوشته شده است.
افت در لوله پنستوک
در بیشتر کتابهای مکانیک سیالات مانند شیمز (Shames) که در دانشگاهها تدریس میشود، افت هد در جریان تراکمناپذیر، یکنواخت و متلاطم (turbulent) در لولهای با سطح مقطع دایره، با رابطه دارسی (Darcy) محاسبه میشود.
$$\large H_f = \frac {2f l V^2} {gd}$$
در رابطه دارسی، $$\large f$$ ضریب اصطکاک، $$\large l$$ طول لوله، $$\large d$$ قطر لوله و $$\large V$$ سرعت جرمی متوسط سیال در لوله است. همچنین فرض میشود که سطح لوله پر است. لوله پنستوک طولانی و دارای قطر بسیار بزرگی است. در نتیجه، انتقال آب از بالادست میتواند افت زیادی را به توربین پلتون تحمیل کند. به این ترتیب باید تعادلی بین ابعاد لوله و جنس آن اتفاق بیفتد تا افت هد به وجود آمده در طول این لوله، در مقایسه با توان خروجی ژنراتور به صرفه باشد. در کاربردهای عملی، سعی میشود رابطه $$\large H_f \: \leq \: 0.1 \:H_G$$ برقرار بماند.
مثال ۱
سؤال: آب با کمک یک لوله پنستوک به طول $$\large 300 \:m$$ و دبی $$\large 2.272 \: \frac {m^3} {s}$$ به یک توربین منتقل میشود. مقدار مجاز افت هد ناشی از اصطکاک در لوله، برابر $$\large 20 \: m$$ است. اگر ضریب اصطکاک $$\large f \: = 0.01$$ باشد، قطر لوله را محاسبه کنید.
پاسخ: میدانیم سرعت سیال در لولهای با سطح مقطع دایره با رابطه $$\large V \: = \frac {4 Q} {\pi d^2}$$ به دست میآید. با ادغام این رابطه و رابطهای که برای $$\large H_ f$$ معرفی شد، میتوانیم قطر لوله را به صورت زیر محاسبه کنیم.
$$\large d^5 \: =\frac {32 \:fl} {g H_f} (\frac {Q} {\pi})^2 = \frac {32 \times 0.01 \times 300} {9.81 \times 20} (\frac {2.272} {\pi})^2 = 0.2559 \\~\\
\large \Rightarrow ~~~ d = 0.7614 \:m$$
افت انرژی در توربین پلتون
در بخش قبلی، افت هد ناشی از اصطکاک مسیر لوله پنستوک را بررسی کردیم. حال به سراغ بقیه موارد میرویم. مقدار هد مؤثر $$\large H _E$$ که هد انتقالی نیز نامیده میشود، در ورودی توربین به صورت زیر به دست میآید.
$$\large H _E = \: H_G \:- H_f = \: z_R - \: z_ N - \: H_f$$
همچنین سرعت فواره (spouting velocity) یا سرعت شعاعی را نیز به صورت $$\large c_o = \sqrt {2 g H_ E}$$ تعریف میکنیم. افت ناشی از اصطکاک $$\large H_f$$، به عنوان افت خارجی به حساب میآید و در برخی کتابها در محاسبه مجموع افتهای داخلی توربین در نظر گرفته نمیشود. در این مقاله، عملکرد و راندمان توربین، همانطور که در ادامه مشاهده خواهید کرد، با توجه به هد انتقالی $$\large H _E$$ محاسبه میشود. عوامل اصلی افت انرژی در توربین به صورت زیر است.
- اصطکاک سیال در نازل
- تبدیل انرژی جنبشی جت به انرژی مکانیکی رانر
- اثرات خارجی مانند اصطکاک یاتاقان و مقاومت باد
حال، موارد بالا را به تفکیک بررسی میکنیم. برای مورد اول، افت هد در نازلها را با $$\large \Delta H _N$$ نشان میدهیم. بنابراین، اختلاف هد به شکل زیر قابل محاسبه است.
$$\large H _E - \: \Delta H _N = \frac {c^2 _1} {2 g}$$
در رابطه بالا، $$\large c_1$$ سرعت جت در خروجی نازل است. راندمان نازل به صورت نسبت انرژی در خروجی نازل به انرژی در ورودی نازل تعریف میشود. رابطه زیر را در نظر بگیرید.
$$\large \eta _ N = \frac {c ^ 2 _ 1} {2 g H _ E}$$
راندمان نازل معمولاً بسیار نزدیک به %$$\large 100$$ است. مقدار دیگری که به عنوان جایگزین راندمان نازل به کار میرود، ضریب سرعت نازل است. این ضریب که آن را با $$\large K _ N$$ نشان میدهیم، به صورت نسبت سرعت در خروجی نازل به سرعت فواره تعریف میشود. به رابطه زیر دقت کنید.
$$\large K _ N = \frac {c _ 1} {c _ 0} ~ , ~~~~~~ \eta _ N = K^2 _ N = \frac {c^2_1} {c^2_0}$$
برای مورد شماره ۲، افت انرژی از رابطه ۱ که پیشتر ارائه شد، به دست میآید. در اینجا برای محاسبه راندمان رانر نیز میتوان از رابطههای ۲ و ۳ کمک گرفت. راندمان هیدرولیکی توربین برابر $$\large \eta _ h$$ است و به صورت نسبت کار مخصوص انجام شده توسط روتور $$\large \Delta W$$ به انرژی مخصوص در دسترس در ورودی نازل $$\large g H _ E$$ تعریف میشود. راندمان هیدرولیکی توربین را میتوان به شکل زیر نوشت.
$$\large \eta _h \: = \frac {\Delta W} {g H_E} = (\frac {\Delta W} {\frac {1} {2} c^2_1}) (\frac {\frac {1} {2} c^2_1} {g H _ E}) = \eta _ R \eta _ N$$
مورد شماره ۳ منجر به کاهش انرژی در انتقال از رانر به محور خروجی میشود. برای تخمین درست این افتها میتوان از یک مدل جریان استفاده کرد. در این مدل، افت انرژی با توان دوم سرعت پره (بشقابک) متناسب فرض شده است. به عبارت دیگر، نسبت افت خارجی به دبی جرمی واحد را برابر $$\large KU^2$$ در نظر میگیریم. در این عبارت، $$\large U$$ سرعت بشقابک و $$\large K$$ هم ثابت بدون بُعد تناسب است. در نتیجه، کار انجام شده توسط محور خروجی در واحد دبی جرمی، از رابطه $$\large \Delta W - KU^2$$ به دست میآید.
راندمان کلی توربین را با $$\large \eta _ o$$ نشان میدهیم و برای محاسبه آن، افتهای خارجی را نیز در نظر میگیریم. به رابطه زیر دقت کنید.
$$\large \eta _ o = \frac {\Delta W - K U^2} {g H _ E}$$
از طرف دیگر، این راندمان برابر با کار منتقل شده از توربین به محور خروجی تقسیم بر انرژی مخصوص موجود در ورودی نازل است. حال میتوان رابطه قبل را به شکل زیر بازنویسی کرد.
$$\large \eta _ o = \eta _R \eta _N - 2K (\frac {U} {c_1})^2(\frac {c^2_1} {2 g H _ E})$$
اکنون اگر از تعریف نسبت سرعت پره به سرعت جت $$\large v = \frac {U} {c_1}$$ و راندمان نازل $$\large \eta _ N = \frac {c^2_1} {c^2_2}$$ استفاده کنیم، راندمان کل به طریق زیر نوشته میشود.
$$\large \eta _ o = \eta _ N (\eta _ R - 2Kv^2) = \eta _ m \eta _ R \eta _ N$$
(رابطه ۴)
عبارت $$\large \eta _ m$$، راندمان مکانیکی است و به صورت $$\large \eta _ m = 1 - \frac {2 K v^2} {\eta _ R}$$ تعریف میشود.
به شکل زیر توجه کنید. در اینجا تغییرات راندمان کل براساس رابطه شماره ۴ و به عنوان تابعی از $$\large v$$ برای ضرایب مختلف $$\large K$$ رسم شده است. همانطور که مشاهده میکنید، با افزایش ضریب $$\large K$$، نقطه پیک راندمان کاهش پیدا میکند و به سمت نقاطی با مقدار $$\large v$$ کوچکتر میرود.
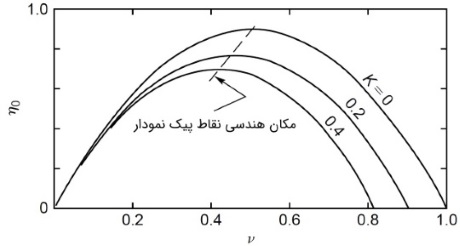
برای یافتن مقدار بهینه $$\large v$$، مشتق رابطه شماره ۴ را برابر صفر قرار میدهیم. در این حالت، مقدار بهینه برای $$\large v$$ با استفاده از رابطه $$\large v_{opt} = \frac {A} {2(A + K)}$$ به دست میآید. در این رابطه $$\large A = 1 - k \cos \beta_2$$ فرض شده است.
مثال ۲
سؤال: در یک توربین پلتون از دو عدد نازل محرک استفاده شده است. توان خروجی و سرعت را به ترتیب برابر $$\large 4.0 \: MW$$ و $$\large 375 \: rev/min$$ در نظر بگیرید. هد مؤثر در نازلها $$\large 200 \: m$$ و ضریب سرعت نازل $$\large K_ N = \: 0.98$$ است. محور نازلها به دایرهای به قطر $$\large 1.5 \: m$$ مماس است. سرعت نسبی جریان در بشقابکها به میزان %$$\large 15$$ کاهش یافته و آب با زاویه $$\large 165$$ درجه منحرف میشود. با صرف نظر از افتهای یاتاقان و هوا، موارد زیر را به دست آورید.
الف) راندمان رانر
ب) اندازه قطر هر جت
پاسخ: الف) ابتدا سرعت پره را محاسبه میکنیم.
$$\large U = \Omega \times r = (375 \times \frac {\pi} {30}) \times \frac {1.5} {2} = 39.27 \: \times 0.75 = 29.45 \: m/s$$
اکنون، سرعت جت را از رابطه زیر مییابیم.
$$\large c_1 \: = K_N \sqrt {2 g H_E} = 0.98 \times \sqrt {2 \times 9.81 \times 200} = 61.39 \: m/s$$
بنابراین $$\large v = \frac {U} {c_1} = 0.4798$$ به دست میآید. به این ترتیب، راندمان رانر به صورت زیر محاسبه میشود.
$$\large \eta _ R = 2v (1 - v) (1 - k \cos \beta _2) \\~\\
\large \eta _ R = 2 \times 0.4798 \times (1 - 0.4798) (1 - 0.85 \times \cos 165^ \circ) = 0.9090$$
ب) توان نظری به صورت $$\large P_ {th} = \rho g Q H_E$$ تعریف میشود و در این مثال، برابر $$\large P_ {th} = \frac {P} {\eta _ R} = \frac {4} {0.909} = 4.4 \:MW$$ است. در نتیجه، دبی به شیوه زیر قابل محاسبه است.
$$\large Q = \frac {P_ {th}} {\rho g H_E} = \frac {4.4 \times 10^6} {9810 \times 200} = 2.243 \: \frac {m^3} {s}$$
حال با استفاده از دبی، میتوانیم مساحت و سپس قطر هر جت را به دست آوریم.
$$\large A_j = \frac {Q} {2c_1} = \frac {2.243} {2 \times 61.39} = 0.01827 \: m^2 \\~\\
\large d_j = 0.5125 \: m$$
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک حرارت و سیالات، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس مهندسی مکانیک
- آموزش مکانیک سیالات
- مجموعه آموزشهای مهندسی مکانیک
- آنتروپی — از صفر تا صد
- پرش هیدرولیکی – از صفر تا صد
- توربوماشین (Turbomachinery) — به زبان ساده
- توربین فرانسیس (Francis Turbine) – از صفر تا صد
^^









