تحلیل سیگنال کوچک دیود | به زبان ساده

در آموزش‌های قبلی مجله فرادرس، با تحلیل سیگنال کوچک در الکترونیک آشنا شدیم. در این آموزش، به تحلیل سیگنال کوچک دیود می‌پردازیم. تحلیل دیود برای سیگنال‌های DC کار ساده‌ای است که معمولا در الکترونیک انجام می‌شود. علاوه بر تحلیل DC، گاهی لازم است دیود را در مدارهایی با سیگنال‌های متغیر با زمان بررسی کنیم. این تحلیل به دلیل ماهیت غیرخطی دیود پیچیده‌تر است. تحلیل مدارهای دیودی اغلب توسط نرم‌افزارهای شبیه‌سازی به سادگی قابل انجام است. اما گاهی تحلیل سیگنال کوچک دیود را به روش دستی و با نوشتن روابط خطی شده و مدار معادل انجام می‌دهیم. در ادامه، با تحلیل سیگنال کوچک دیود آشنا می‌شویم.

تحلیل سیگنال کوچک دیود

مفهوم عملکرد سیگنال کوچک دیود یا هر عنصر دیگر، در واقع این است که در مدار، یک سیگنال متغیر با زمان با دامنه کوچک روی یک مقدار DC وجود دارد که ممکن است بزرگ باشد.

در نتیجه، تحلیل مدار را می‌توان به دو بخش تقسیم کرد:

• بایاس DC
• سیگنال AC با دامنه کوچک

و جواب‌ها با استفاده از اصل برهم‌نهی یا جمع آثار با یکدیگر جمع می‌شوند. از آنجا که بخش AC کوچک است، مدار را می‌توان خطی‌سازی کرد و اصل جمع آثار را به کار برد (دقت کنید که در حالت کلی، برای یک مدار غیرخطی، نمی‌توان از جمع آثار به صورت دقیق استفاده کرد).

برای مثال، شکل زیر را در نظر بگیرید که در آن، $$v _ d ( t)$$ یک شکل موج متغیر با زمان و احتمالاً متناوب مانند سینوسی یا مثلثی است.

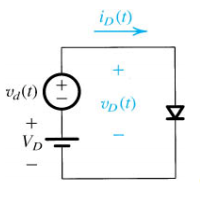
کاربرد $$V_ D$$ در این مدار، تنظیم عملکرد دیود حول یک نقطه روی منحنی مشخصه $$i-v$$ بایاس مستقیم است. این نقطه، «نقطه ساکن» (Quiescent Point) یا نقطه Q نامیده می‌شود و فرایند تنظیم این مقادیر DC، «بایاس کردن» دیود نام دارد.

ولتاژ کل در هر لحظه $$t$$ برابر با مجموع مؤلفه‌های DC و AC است:

$$\large v _ D ( t ) = V _ D + v _ d ( t ) \;\;\;\;\; ( 1 )$$

که در آن، سیگنال AC به اندازه کافی کوچک بوده و دیود تقریباً‌ به صورت خطی عمل می‌کند.

جریان دیود به صورت $$i _ D ( t) >> I_ S$$ است، به گونه‌ای که داریم:

$$\large \begin {align*} i _ D ( t) \approx I _ S e ^ { \frac {v _ D ( t ) } { n V _ T } } = \underbrace { I_ S e ^ { \frac { V _ D } { n V _ T } } } _ { = I _ D } e ^ { \frac {v _ d ( t ) } { n V _ T } } \end {align*}$$

یا

$$\large \begin {align*} i _ D ( t) \approx I _ D e ^ { \frac {v _ d ( t ) } { n V _ T } } \end {align*} \;\;\;\;\; ( 2 )$$

که $$I_ D$$ جریان DC دیود است.

رابطه بالا یک رابطه نمایی است و می‌توانیم از بسط مک لورن تابع نمایی به صورت زیر در آن استفاده کنیم:

$$\large e ^ x = 1 + x + \frac { x ^ 2 } { 2 ! } + \cdots$$

و اگر $$v _ d ( t)$$ به اندازه کافی کوچک باشد، به گونه‌ای که $$v _ d ( t) / ( n V _ T) << 2$$، تنها دو جمله سری را در نظر می‌گیریم:‌

$$\large e ^ { \frac {v _ d ( t ) } { n v _ T } } \approx 1 + \frac {v _ d ( t)} { n V _ T } \;\;\;\;\; ( 3 )$$

با جایگذاری (۳)‌ در (۲)، خواهیم داشت:

$$\large i _ D ( t ) \approx I _ D + \frac { I _ D } { n V _ T } v _ d ( t ) \;\;\;\;\; ( 3 )$$

بنابراین، اگر $$v _ d ( t)$$ به اندازه کافی کوچک باشد، از معادله آخر در می‌یابیم که $$i _ D$$ مجموع (یا جمع آثار) دو مؤلفه سیگنال‌های DC و AC است. آنچه که انجام می‌دهیم، خطی‌سازی مسئله با محدود کردن بخش AC ولتاژ $$v _ D$$ به مقادیر کوچک است. این پارامتر خطی شده است، زیرا در (۴) جملات با $$v _ d ^ 2$$ و بالاتر همگی به اندازه‌ای کوچک هستند که می‌توان از آن‌ها چشم‌پوشی و از معادله حذف کرد، به گونه‌ای که $$i _ D ( t)$$ تنها به $$v _ D$$ بستگی دارد.

واحد جمله $$n V _ T / I_D$$ در (۴)، اهم است و مقاومت سیگنال کوچک نامیده می‌شود:

$$\large r _ d \equiv \frac { n V _ T } { I _ D } \; \; [\mathrm {\Omega}] \;\;\;\;\; ( 5 )$$

از دیدگاه فیزیکی، $$r _ d$$ معکوس شیب خط مماس در نقطه بایاس روی منحنی مشخصه دیود است.

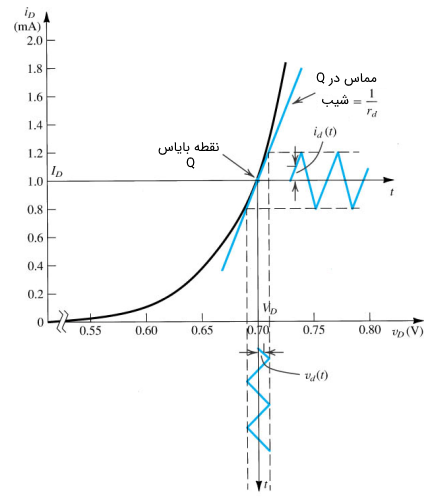
توجه کنید که $$r _ d$$ بسته به بایاس DC تغییر می‌کند. شکل زیر این موضوع را به خوبی نشان می‌دهد.

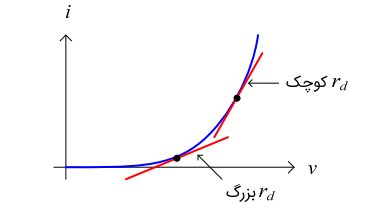
(توجه کنید که این $$r _ d$$ یک کمیت اساساً متفاوت با $$r _ D$$ است که در مدل تکه‌ای خطی (PWL) دیود استفاده می‌شود).

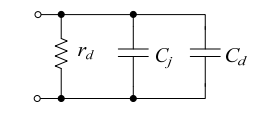
مدار معادل عملکرد سیگنال کوچک دیودها به صورت زیر است.

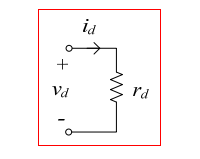
از آنجا که عملکرد دیود را خطی کرده‌ایم (با محدود کردن تحلیل به سیگنال‌های AC کوچک)، می‌توانیم از جمع آثار برای تحلیل ترکیب سیگنال‌های DC و AC استفاده کنیم.

بدین معنا که «تحلیل سیگنال با حذف همه منابع DC انجام می‌شود.» (یعنی با اتصال کوتاه منابع ولتاژ DC و مدار باز منابع جریان DC) «و جایگزین کردن دیود با مقاومت سیگنال کوچک $$r _ d$$ آن.»

این فرایند با شکل زیر قابل بیان است.

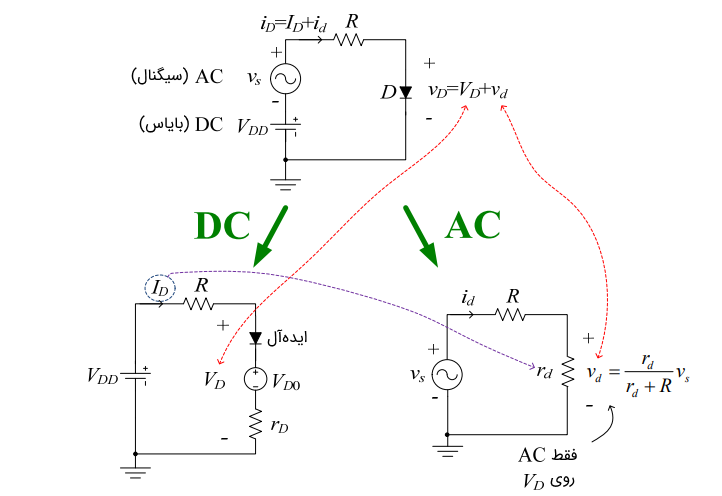
مثال تحلیل سیگنال کوچک دیود

در مدار شکل زیر، مقدار $$v _ D$$ را وقتی که $$V ^ + = 10 + 1 \cdot \cos ( 2 \pi \cdot 60 t )$$ ولت است.

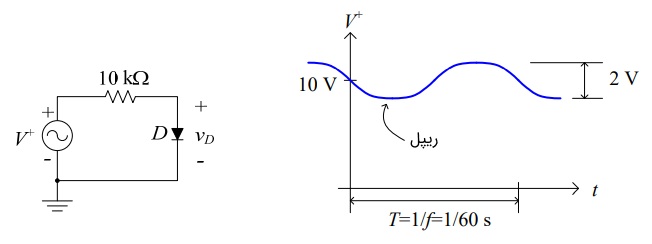
مشخصات دیود به صورت زیر است:

• افت ولتاژ ۰٫۷ ولت در $$1\; \text{mAdc}$$
• $$n = 2$$.

فیلم آموزش مدارهای الکتریکی ۱ – جامع و کاربردی در فرادرس

کلیک کنید

همان‌طور که گفتیم، برای سیگنال‌های AC کوچک، می‌توانیم تحلیل DC را جدا از تحلیل AC (یعنی خطی شده) انجام دهیم. بنابراین، لازم است از بایاس DC شروع کنیم. با فرض $$V_ D \approx 0.7 \;\text{V}$$ برای یک دیود سیلیکونی، جریان DC برابر است با:

$$\large I _ D = \frac { 10 - 0.7 } { 10,000} = 0.93 \; \text {mA}$$

از آنجا که $$I _ D \approx 1 \; \text{mA}$$ است، مقدار $$V_ D$$ بسیار نزدیک به مقدار فرض شده خواهد بود.

در این بایاس DC، مقاومت سیگنال کوچک در نقطه Q برابر است با:

$$\large r _ d = \frac { n V _ T } { I _ D } = \frac { 2\times25 \times 10 ^ { - 3 } } { 0.93 \times 10 ^ { - 3 } } = 53.8 \; \mathrm {\Omega}$$

از $$r _ d$$ به عنوان مقاومت معادل در مدل سیگنال کوچک دیود استفاده خواهیم کرد.

ولتاژ AC دو سر دیود از تقسیم ولتاژ به دست می‌آید:

$$\large \begin {align*} v _ d ( t) & = \frac { r _ d } { r _ d + 10,000} v _ s = \frac { 53.8} { 53.8+10,000} \cdot \cos (\omega t ) \\ & 5.35 \cos (\omega t ) \; \text {mV} \end {align*}$$

بنابراین، اندازه ولتاژ دیود به صورت زیر خواهد بود:

$$\large v _ d = 5.35 \; \mathrm { m V _ p } = 10.70\; \mathrm { m V _ { pp}}$$

که اندیس $$\mathrm {p}$$ مقدار پیک و اندیس $$\mathrm { pp }$$ مقدار پیک تا پیک را نشان می‌دهد.

بنابراین، کل ولتاژ $$v _ D$$ دیود برابر با مجموع ولتاژهای DC و AC خواهد بود:

$$\large v _ D ( t ) = 0.7 + 0.00535 \cos (\omega t ) \; \mathrm {V}$$

اما در چه جایی مجازیم از فرض سیگنال کوچک برای این مسئله استفاده کنیم؟ همان‌طور که پیش‌تر گفتیم، باید بررسی کنیم $$v _ d ( t ) / ( n V _ T ) << 2$$ باشد:

$$\large \frac { v _ d } { n V _ T } = \frac { 5.35 \times 10 ^ { - 3 } } { 2\times 25 \times 10 ^ { - 3 } } = 0.107$$

که بسیار کوچک‌تر از $$2$$ است. بنابراین، فرض سیگنال کوچک معتبر است.

دقت کنید که در این مدار، ریپل ولتاژ‌ خروجی کاهش یافته است. در ورودی، ریپل $$2/10$$ یا $$20$$ درصد مؤلفه DC است، در حالی که در خروجی، ریپل $$0.0107/0.7$$ یا $$1.5$$ درصد مؤلفه DC است.

مدل دیود در فرکانس بالا

مدل دیود در فرکانس بالا یک مدل AC کاملاً مقاومتی برای دیود است که وقتی فرکانس سیگنال‌های AC به اندازه کافی کوچک باشد، نتایج مناسبی خواهد داشت.

در فرکانس‌های بالا، لازم است اثرات ناشی از این سیگنال‌های متغیر با زمان و جداسازی بار در ناحیه تخلیه (تهی) و ناحیه‌های توده‌ای p و n را در نظر بگیریم (این جداسازی بار در اثر بایاس مستقیم است).

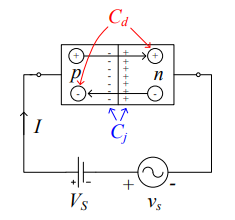
در داخل قطعه و ناحیه تخلیه، یک میدان الکتریکی وجود دارد. برای سیگنال‌های AC، این میدان الکتریکی با زمان تغییر می‌کند.

همان‌طور که از الکترومغناطیس می‌دانیم، یک میدان الکتریکی متغیر با زمان یک جریان جابه‌جایی (Displacement Current) است. اثرات جابه‌جایی جریان با خازن‌های مدار معادل مدل می‌شوند.