تحلیل سیگنال کوچک در الکترونیک | به زبان ساده

«تحلیل سیگنال کوچک» (Small-Signal Analysis) یک روش تحلیل رایج در مهندسی الکترونیک است که رفتار مدارهای الکترونیکی متشکل از قطعات غیرخطی را در قالب یک معادله خطی تقریب می‌زند. این روش در آن دسته از مدارهای الکترونیکی کاربرد دارد که در آن‌ها سیگنال‌های جریان‌‌ و ولتاژ AC مدار، نسبت به جریان‌ها و ولتاژهای DC انداره کوچکی داشته باشند. مدل سیگنال کوچک، یک مدار معادل AC است که در آن عناصر مدار غیر خطی با عناصر خطی جایگزین می‌شوند و مقادیر آن‌ها با تقریب مرتبه اول (خطی) منحنی مشخصه آن‌ها در نزدیکی نقطه کار تخمین زده می‌شود. در این آموزش، با روش تحلیل سیگنال کوچک آشنا می‌شویم.

تحلیل سیگنال کوچک

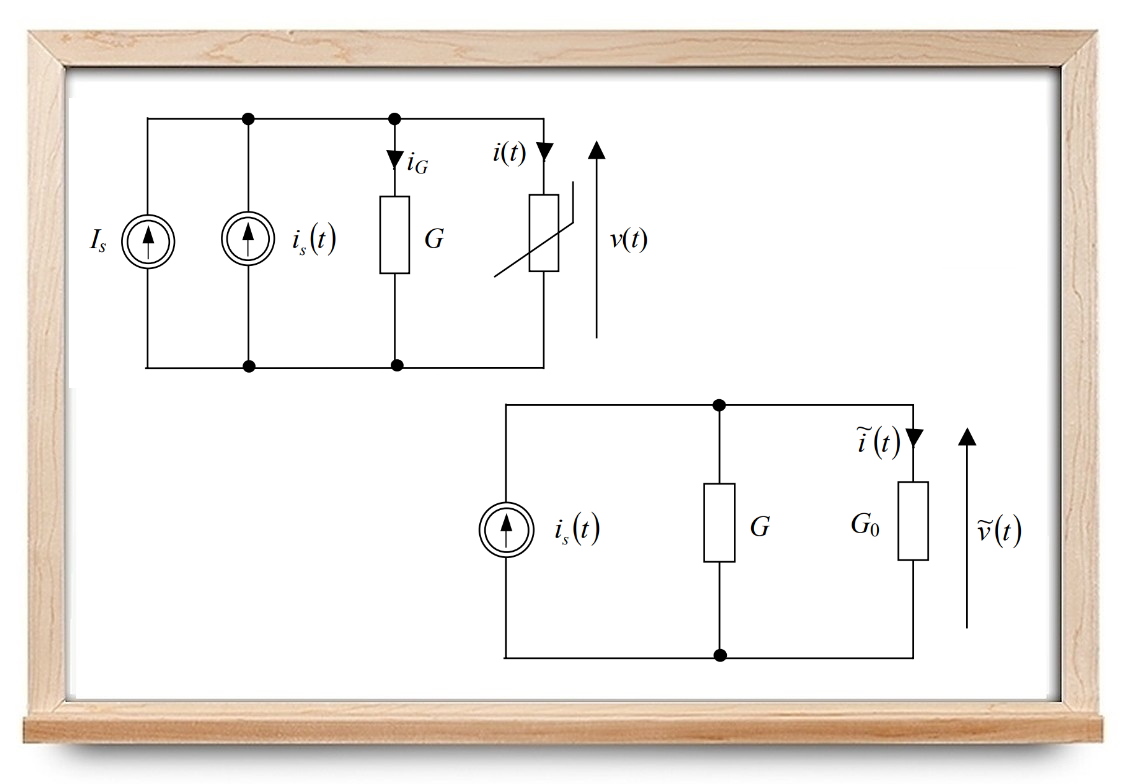
مدار شکل ۱ را در نظر بگیرید که معادله مقاومت غیرخطی آن، $$i = g ( v )$$ است.

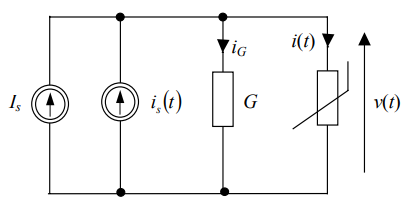
نمودار مربوط به این معادله در شکل ۲ رسم شده است.

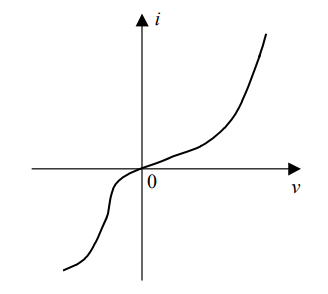
$$I_ s$$ یک منبع جریان DC و $$i _ s ( t)$$ یک منبع جریان متغیر با زمان است. فرض می‌کنیم قدر مطلق $$i _ s ( t )$$ در همه لحظات از منبع DC کوچک‌تر باشد.

در ادامه، نقطه کار را پیدا می‌کنیم.

محاسبه نقطه کار

برای یافتن نقطه کار، منبع جریان $$i _ s ( t)$$ را برابر با صفر قرار داده و فرض می‌کنیم یک مدار DC با منبع $$I _ s$$ داریم. ولتاژها و جریان‌های DC مدار را با حروف بزرگ نمایش می‌دهیم. در نتیجه، خواهیم داشت:

$$\large  I _ s - GV = I , \quad \quad (1)$$

$$\large  I = g ( V ) . \quad \quad (2)$$

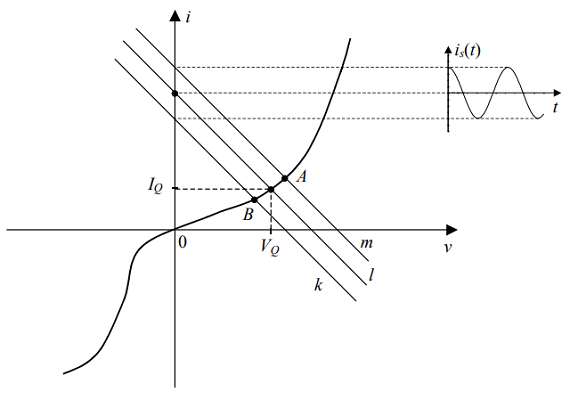
مجموعه معادلات (۱) و (۲) را به صورت گرافیکی، مطابق آنچه در شکل ۳ نشان داده شده است، حل می‌کنیم و نقطه کار $$(V _ Q , I _ Q )$$ را به دست می‌آوریم.

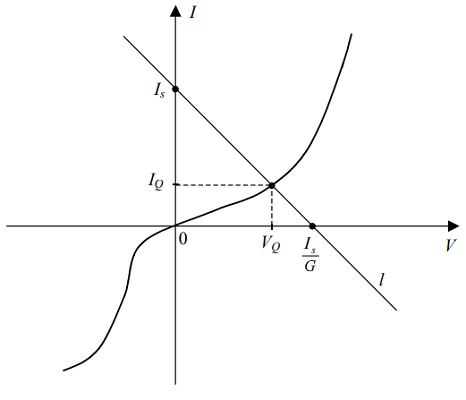
اکنون مدار شکل ۱ را در نظر بگیرید که شامل منبع $$i _ s ( t)$$ است. این مدار با معادلات زیر توصیف می‌شود:

$$\large i ( t) = I _ s + i _ s ( t) - G v ( t) , \quad \quad (3)$$

$$\large i ( t) = g ( v ( t )). \quad \quad (4)$$

برای هر لحظه $$t$$، نقطه $$( v (t ) , i ( t) )$$ که در معادله (۳) صدق می‌کند، روی خط راستی موازی با خط $$l$$ قرار دارد که در شکل ۳ نشان داده شده است. اگر $$i _ s ( t) = A \cos \omega t$$ باشد، آنگاه این خطوط راست توسط خطوط $$k$$ و $$m$$ که در شکل ۴ نشان داده‌ شده‌اند، محدود می‌شوند. نقاط تقاطع با منحنی مشخصه $$i = g ( v )$$ مقادیر کران‌دار $$v ( t)$$ و $$i ( t)$$ را نشان می‌دهد. بنابراین، برای همه $$t$$ها نقاط $$( v ( t) , i ( t) )$$ روی کمان $$A B$$ منحنی مشخصه صدق می‌کنند. این کمان را می‌توان با یک قطعه خطی تقریب زد.

ولتاژ‌ $$v ( t )$$ و جریان $$i ( t)$$ را به صورت زیر نمایش می‌دهیم:

$$\large v ( t ) = V_ Q + \tilde v ( t)  \quad \quad ( 5 )$$

$$\large i ( t ) = I _ Q + \tilde i ( t)  \quad \quad ( 6 )$$

که در آن، $$\tilde v ( t)$$ و $$\tilde i ( t)$$ را می‌توان به عنوان جابه‌جایی‌های کوچک حول نقطه کار در نظر گرفت. با جایگذاری (۵) و (۶) در (۴)، خواهیم داشت:

$$\large I _ Q + \tilde i ( t ) = g \left ( V_ Q + \tilde v (t ) \right ) . \quad \quad ( 7 )$$

سمت راست معادله (۷) را با سری تیلور بسط می‌دهیم و از جملات مرتبه بالای آن چشم‌پوشی می‌کنیم:

$$\large I _ { Q } + \tilde { i } ( t ) = g \left ( V _ { Q } \right ) + \left . \frac { \mathrm { d } g } { \mathrm { d } v } \right | _ { v = V _ { Q } } \tilde { v } ( t ) . \quad \quad (8)$$

از آنجا که $$I _ Q = g ( V _ Q )$$، معادله (۸) به معادله زیر کاهش می‌یابد:

$$\tilde { i } ( t ) = G _ { 0 } \tilde { v } ( t ) , \quad \quad (9)$$

که در آن،

$$\large G _ { 0 } = \left . \frac { \mathrm { d } g }{ \mathrm { d } v } \right | _ { v = V _ { Q } } . \quad \quad ( 10 )$$

در ادامه، (۵) و (۶)‌ را در (۳)‌ قرار می‌دهیم:

$$\large I _ { Q } + \tilde { i } ( t ) = I _ { s } + i _ { s } ( t ) - G \left ( V _ { Q } + \tilde { v } ( t ) \right ) . \quad \quad (11)$$

از آنجا که $$I _ Q = I _ s - G ( V _ Q )$$، خواهیم داشت:

$$\large \tilde { i } ( t ) = i _ { s } ( t ) - G \tilde { v } ( t ). \quad \quad ( 12 )$$

معادله‌های (۹) و (۱۲) مدار معادل سیگنال کوچک شکل ۵ هستند.

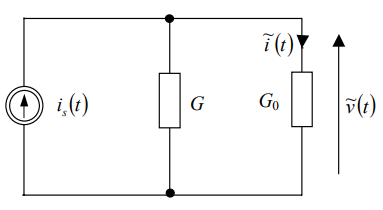
این مدار خطی است و این امکان را فراهم می‌کند که سیگنال‌های کوچک $$\tilde v ( t)$$ و $$\tilde i ( t)$$ را به دست آوریم:

$$\large \tilde v ( t) = \frac { i _ s ( t ) } { G + G _ 0 } , \quad \quad (13)$$

$$\large \tilde i ( t) = i _ s ( t) \frac { G_ 0 } { G + G _ 0 } . \quad \quad (14)$$

مدل سیگنال کوچک یک مدار دیودی

مدار شکل ۶ را در نظر بگیرید که توسط منبع ولتاژ‌ دی‌سی $$V _ s$$ و منبع ولتاژ‌ سیگنال کوچک $$v _ s ( t)$$ کار می‌کند.

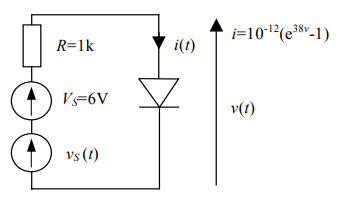
برای یافتن مدل سیگنال کوچک این مدار، ابتدا نقطه کار DC را به دست می‌آوریم. بدین منظور، مدار شکل ۷ را تحلیل می‌کنیم.

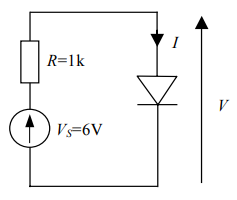
معادله زیر مدار شکل ۷ را توصیف می‌کند:

$$\large 1 0 ^ { - 1 2 } \left ( e ^ { 3 8 V } - 1 \right ) + 0 . 0 0 1 V - 0 . 0 0 6 = 0 ,$$

که می‌توان آن را به فرم زیر نوشت:

$$\large e ^ { 3 8 V } + 1 0 ^ { 9 } V - 6 \cdot 1 0 ^ { 9 } = 0 . \quad \quad ( 15 )$$

این معادله را با استفاده از روش نیوتن-رافسون حل می‌کنیم:

$$\large V ^ { ( j + 1 ) } = V ^ { ( j ) } - \frac { \mathrm { e } ^ { 3 8 N ^ { ( j ) } } + 1 0 ^ { 9 } V ^ { ( j ) } - 6 \cdot 1 0 ^ { 9 } } { 3 8 \mathrm { e } ^ { 3 8 V ^ { ( j ) } } + 1 0 ^ { 9 } } , \quad \quad ( 16 )$$

با استفاده از حدس اولیه $$V ^ {(0)} = 0.6$$، مقادیر $$V ^ { ( 1 ) } = 0 . 59 1$$، $$V ^ { ( 2 ) } = 0 . 5 9 0$$ و $$V ^ { (3 ) } = 0 . 5 9 0$$ را به دست خواهیم آورد. در نتیجه، $$V _ 0 = 0.590$$ را در نظر می‌گیریم و مقادیر زیر را خواهیم داشت:‌

$$\large G _ { 0 } = \left . \frac { \mathrm { d } i } { \mathrm { d } v } \right | _ { v = V _ { 0} } = 3 8 \cdot 1 0 ^ { - 1 2 } \mathrm { e } ^ { 3 8 \cdot 0 .5 9 0 } = 0 . 2 0 7 \; S ,$$

یا

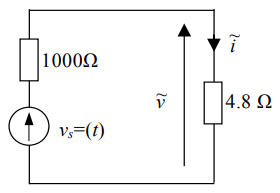
$$\large R _ { 0 } = G _ { 0 } ^ { - 1 } = 4 . 8 \; \Omega .$$

مدل سیگنال کوچک در شکل ۸ نشان داده شده است.

مدل سیگنال کوچک یک مدار ترانزیستوری

مدار تقویت کننده ساده BJT شکل ۹ را در نظر بگیرید.

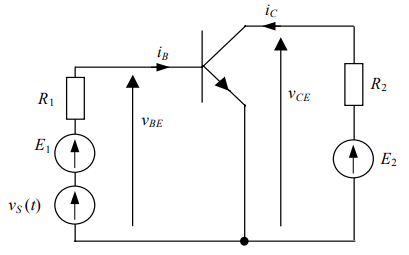
$$E_ 1$$ و $$E_ 2$$ منابع ولتاژ DC هستند و $$v _ s ( t)$$ تغییرات زمانی کوچک منبع ولتاژ را نشان می‌دهد. در ادامه، نقطه کار را به دست می‌آوریم.

برای به دست آوردن نقطه کار، ابتدا $$v _ s ( t)$$ را برابر با صفر قرار می‌دهیم و مدار DC تحت منابع ولتاژ DC با نام‌های $$E _ 1$$ و $$E_ 2$$ را حل می‌کنیم که به صورت گرافیکی در شکل‌های ۱۰ و ۱۱ نشان داده شده‌اند.

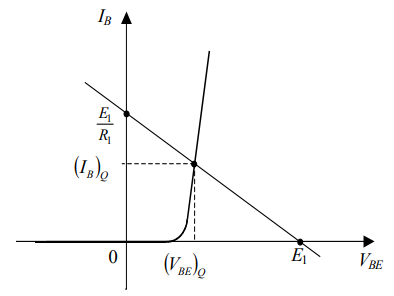
نقطه کار را با $$\left ( V _ { BE} \right ) _ Q$$، $$\left ( I _ { B} \right ) _ Q$$، $$\left ( V _ { CE } \right ) _ Q$$ و $$\left ( I _ { C } \right ) _ Q$$ مشخص می‌کنیم.

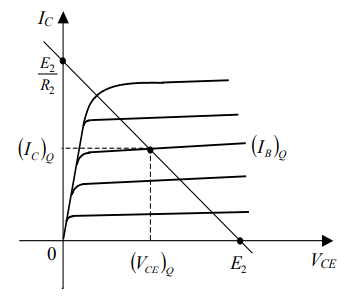
به طور کلی، نقطه کار جواب مجموعه معادلات هایبرید توصیف کننده ترانزیستور است:

$$\large V _ { B E } = \hat v _ { B E } ( I _ B , V _ { CE} ) \quad \quad (17)$$

$$\large I _ { C } = \hat i _ { C } ( I _ B , V _ { CE} ) \quad \quad (18)$$

معادلات توصیف کننده شاخه‌های $$R_ 1 , E_ 1$$ و $$R _ 2 , E _ 2$$ به صورت زیر هستند:

$$\large V _ { B E } = E _ 1 - R_ 1 I _ B, \quad \quad (19)$$

$$\large V _ { C E } = E _ 2 - R_ 2 I _ C .\quad \quad (19)$$

اکنون مدار شکل ۹ را در نظر می‌گیریم که شامل ولتاژ سیگنال کوچک $$v _ s ( t)$$ است. در این مدار، ولتاژها و جریان‌ها با زمان تغییر می‌کنند: $$v _ { BE} ( t) , i _ B ( t) , v _ { CE} ( t) , i _ C ( t)$$. این ولتاژها و جریان‌ها را به صورت زیر نمایش می‌دهیم:

$$\large v _ { B E } ( t ) = ( V _ {BE} ) _ Q + \tilde v _ 1 ( t) , \quad \quad (21)$$

$$\large i _ { B } ( t ) =\left ( I _ { B } \right ) _ { Q } + \tilde { i }_ 1 ( t ) , \quad \quad (22)$$

$$\large v _ { C E } ( t ) = \left ( V _ { C E } \right ) _ { Q} + \tilde { v } _ { 2 } ( t ) , \quad \quad (23)$$

$$\large i _ { C } ( t ) = \left ( I _ { C } \right ) _ { Q } + \tilde { i } _ { 2 } ( t) , \quad \quad (24)$$

که در آن، $$\tilde v _ 1 ( t)$$، $$\tilde i _ 1 ( t)$$، $$\tilde v _ 2 ( t)$$ و $$\tilde i _ 2 ( t)$$ جابه‌جایی‌های حول نقطه کار را نشان می‌دهند. این معادلات را به معادلات هایبرید تبدیل می‌کنیم:

$$\large \begin {align*} \left ( V _ { B E } \right ) _ { Q } + \widetilde { v } _ { 1 }( t ) & = \hat { v } _ { B E } \left ( \left ( I _ { B } \right ) _ { Q } + \tilde { i } ( t ) , \left ( V _ { C E } \right ) _ { Q } + \widetilde { v } _ { 2 } ( t ) \right ) , \quad \quad (25) \\ \left ( I _ { C } \right ) _ { Q } + \tilde { i } _ { 2 }( t ) & = \hat { i } _ { C } \left ( \left ( I _ { B } \right ) _ { Q } + \tilde { i } ( t ) , \left ( V _ { C E } \right ) _ { Q } + \widetilde { v } _ { 2 } ( t ) \right ), \quad \quad (26) \end {align*}$$

اکنون، توابع را در سمت راست و حول نقطه کار به سری تیلور بسط می‌دهیم و از جملات مرتبه بالاتر چشم‌پوشی می‌کنیم:

$$\large \begin {align*} \left ( V _ { B E } \right ) _ { Q } + \widetilde { v } _ { 1 }( t ) & = \hat { v } _ { B E } \left ( \left ( I _ { B } \right ) _ { Q } , \left ( V _ { C E } \right ) _ { Q } \right ) + \left . \frac { \partial \hat { v } _ { B E } } { \partial i _ { B } } \right| _ { Q } \tilde { i } ( t ) + \left . \frac { \partial \hat { v } _ { B E } } { \partial v _ { C E } } \right | _ { Q } \tilde { v } _ { 2 } ( t ) \quad \quad (27) \\ \left ( I _ { C } \right ) _ { Q } + \tilde { i }_2 ( t ) & = \hat { i } _ { C } \left ( \left ( I _ { B } \right ) _ { Q } , \left ( V _ { C E } \right ) _ { Q } \right ) + \frac { \partial \hat { i } _ { C } }{ \partial i _ { B } } _ { Q } \tilde { i } _ { 1 } ( t ) + \left . \frac { \partial \hat { i } _ { C } } { \partial v _ { C E } } \right| _ { Q } \tilde { v } _ { 2 } ( t ) . \quad \quad (28) \end {align*}$$

با در نظر گرفتن معادله‌های (۱۷) و (۱۸)، خواهیم داشت:

$$\large \tilde { v } _ { 1 } ( t ) = \left . \frac { \partial \hat { v } _ { B E } } { \partial i _ { B } } \right | _ { Q } \tilde { i }_ 1 ( t ) + \left . \frac { \partial \hat { v } _ { B E } } { \partial v _ { c E } } \right | _ { Q } \tilde { v } _ { 2 } ( t ) , \quad \quad ( 29 )$$

$$\large \tilde { i } _ { 2 } ( t ) = \left . \left . \frac { \partial \hat { i } _ { c } } { \partial i _ { B } } \right | _ { Q } \right . { \tilde { i } _1 ( t ) + \left . \frac { \partial \hat { i } _ { C } }{ \partial v _ { C E } } \right | _ { Q } } \tilde { v } _ { 2 } ( t ) . \quad \quad (30)$$

مجموعه معادلات را می‌توان به صورت زیر بازنویسی کرد:

$$\large \begin{align*} \widetilde { v } _ { 1 } ( t ) & = h _ { 1 1 } \tilde { i } ( t ) + h _ { 1 2 } \tilde { v } _ { 2 } ( t ) , \quad \quad (31)\\ \tilde { i } ( t ) & = h _ { 2 1 } \tilde { i } ( t ) + h _ { 2 2 } \widetilde { v } _ { 2 } ( t ) , \quad \quad (32) \end {align*}$$

که در آن‌ها،

$$\large h _ { 1 1 } = \left . \frac { \partial \hat { v } _ { B E } } { \partial i _ { B } } \right | _ { Q } , h _ { 1 2 } = \left . \frac { \partial \hat { v } _ { B E } } { \partial v _ { C E } } \right | _ { Q } , h _ { 2 1 } = \left . \frac { \partial \hat { i } _ { C } } { \partial i _ { B } } \right | _ { Q } , h _ { 2 2 } = \left . \frac { \partial \hat { i } _ { C } } { \partial v _ { C E } } \right | _ { Q } .$$

مدار توصیف شده با معادلات (۳۱) و (۳۲) مدل سیگنال کوچک ترانزیستور نامیده می‌شود که در شکل ۱۲ نشان داده شده است.

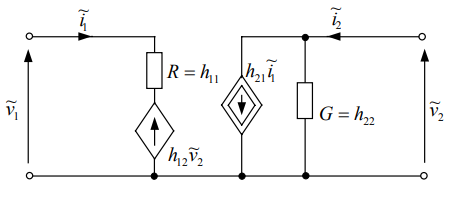
مقادیر متداول ضرایب این‌گونه‌اند: $$h _ { 1 1 } = 1 0 ^ { 3 } \;\Omega$$، $$h _ { 1 2 } = 2 \cdot 1 0 ^ { - 4 }\Omega$$، $$h _ {21} = 50 \; \mathrm {S}$$ و $$h _ {22} = 10 ^ { - 5 } \; \mathrm {S}$$.

اکنون شاخه‌های مقاومت-منبع مدار شکل ۹ را در نظر گرفته و معادلات را می‌نویسیم:

$$\large v _ { B E } = E _ { 1 } + v _ { s } ( t ) - R _ { 1 } i _ { B } , \quad \quad (33)$$

$$\large v _ { C E } = E _ { 2 } - R _ { 2 } i _ { C } . \quad \quad (34)$$

با جایگذاری (۲۱) و (۲۲) و در نظر گرفتن (۱۹) و (۲۰)، خواهیم داشت:

$$\large \widetilde v _ 1 ( t) = v _ s ( t ) - R_ 1 \widetilde i _ 1 ( t) , \quad \quad ( 3 5 )$$

$$\large \widetilde v _ 2 ( t) = - R_ 2 \widetilde i _ 2 ( t) . \quad \quad ( 3 6 )$$

با ترکیب معادلات (۳۵) و (۳۶) با معادلات (۳۱) و (۳۲) که مدل سیگنال کوچک ترانزیستور را توصیف می‌کنند، مدار معادل سیگنال کوچک مدار تقویت‌کننده شکل ۱۳ را به دست خواهیم آورد.

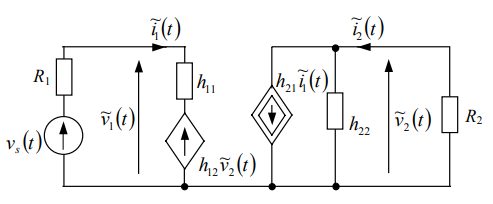
اکنون، بهره ولتاژ این مدار را که به صورت $$\tilde  v _ 2 / v _ s$$ تعریف می‌شود، پیدا می‌کنیم. برای این کار، معادلات (۲۹) و (۳۰) و (۳۵) و (۳۶) را می‌نویسیم (که مدار را توصیف می‌کنند) و آن‌ها را به صورت زیر بازنویسی می‌کنیم:‌

$$\large \begin {align*} \tilde { i } _ { 2 } ( t ) & = - \frac { \widetilde { v } _ { 2 } ( t ) } { R _ { 2 } } = h _ { 2 1 } \widetilde { i } _ { 1 }( t ) + h _ { 2 2 } \widetilde { v } _ { 2 } ( t ) , \\ \widetilde { v } _ { 2 } & = \frac { - h _ { 2 1 } }{ h _ { 2 2 } + \frac { 1 } { R _ { 2 } } } \tilde { i } _ 1 ( t ) , \\ v _ { s } ( t ) - R _ { 1 } \tilde { i } _ { 1 } ( t ) & = h _ { 1 1 } \tilde { i } _ 1 ( t ) + h _ { 1 2 } \frac { \left ( -h _ { 2 1 } \right ) } { h _ { 2 2 } + \frac { 1 } { R _ { 2 } } } \tilde { i } _1 ( t ) , \\ \tilde { i } _ 1 ( t ) & = \frac { \left ( h _{22} + \frac 1 {R _ {2}} \right ) v _ s ( t ) } { \left ( h _ { 1 1 } + R _ { 1 } \right ) \left ( h _ { 2 2 } + \frac { 1 } { R _ 2 } \right ) - h _ { 1 2 } h _ { 2 1 } } , \\ \frac { \tilde { v } _ { 2 } ( t ) } { v _ { s } ( t ) } & = \frac {- h _ { 2 1 } } { \left ( h _ { 1 1 } + R _ { 1 } \right ) \left ( h _ { 2 2 } + \frac { 1 } { R _ { 2 } } \right ) - h _ { 1 2 } h _ { 2 1 } } . \quad \quad (37) \end {align*}$$

در فرمول بهره ولتاژ (۳۷)، این مقادیر را قرار می‌دهیم: $$R _ 1 = R_ 2 = 1 k \Omega$$، $$h _ {11} = 1 k \Omega$$، $$h _ {12} = 2\cdot 10 ^ {-4} k \Omega$$، $$h _ {21} = 50 S$$ و $$h _ {22} = 10 ^ {-5} S$$ و خواهیم داشت:

$$\large \frac { \tilde v _ 2 ( t) } { v _ s ( t ) } = -24.8 .$$

مدل سیگنال کوچک یک مدار عمومی

مداری را با مقاومت‌ها و سلف‌ها و خازن‌های خطی و غیرخطی و منابع کنترل شده خطی در نظر بگیرید که با یک منبع DC و یک منبع متغیر با زمان کوچک کار می‌کند. برای تشکیل مدار معادل سیگنال کوچک ابتدا نقطه کار DC را پیدا می‌کنیم. بدین منظور، منبع متغیر با زمان کوچک را برابر با صفر قرار می‌دهیم و مدار را تنها با منبع DC بررسی می‌کنیم.

در نتیجه، یک مدار DC را با اتصال کوتاه کردن همه سلف‌ها و مدار باز کردن همه خازن‌ها به دست می‌آوریم. مدار حاصل را می‌توان با هر روشی از روش‌های تحلیل مدارهای مقاومتی حل کرد. اگر مدار غیرخطی باشد، از روش نیوتن-رافسون استفاده می‌کنیم. نقطه کار $$Q$$ را با جریان شاخه $$( I _ j ) _ Q$$ و ولتاژهای شاخه $$( V _ j ) _ Q$$ مشخص می‌کنیم.

در مداری که با منبع DC و منبع متغیر با زمان کوچک تغذیه می‌شود، همه ولتاژها و جریان‌های شاخه‌ها به زمان وابسته است. ولتاژ‌ هر شاخه را به صورت زیر نمایش می‌دهیم:

$$\large v ( t) = V _ Q + \tilde v ( t)$$

و جریان هر شاخه نیز به صورت زیر خواهد بود:

$$i ( t) = I _ Q + \tilde { i } ( t )$$

که در آن، $$\tilde v ( t)$$ و $$\tilde i ( t)$$ جابه‌جایی‌های کوچک حول نقطه کار هستند. از آنجا که هر دو ولتاژ $$v _ j ( t )$$ و $$( V _ j ) _ Q$$ در KVL در یک حلقه دلخواه صدق می‌کنند، می‌توان گفت که $$\tilde  v _ j ( t)$$ نیز در KVL در هر حلقه دلخواه صدق می‌کند.

به طور مشابه، می‌توان گفت جریان‌های $$\tilde i _ j ( t)$$ در KCL برای همه گره‌ها صدق می‌کند.

اکنون اجزای مدار را در نظر گرفته و آن‌ها را برحسب سیگنال‌های متغیر با زمان توصیف می‌کنیم.

مقاومت غیرخطی با معادله زیر بیان می‌شود:

$$\large i ( t)  = g ( v ( t)) . \quad \quad (38)$$

عبارت‌های $$i ( t) = I _ Q + \tilde i ( t)$$ و $$v ( t) = V _ Q + \tilde v ( t)$$ را جایگذاری کرده و تابع $$g ( v ( t))$$ را با سری تیلور حول نقطه کار بسط می‌دهیم (با چشم‌پوشی از جملات مرتبه بالاتر):

$$\large I _ { Q } + \tilde { i } ( t ) = g \left ( V _ { Q } \right ) + \left . \frac { \mathrm { d } g } { \mathrm { d } v } \right | _ { v = V _ { Q } } \tilde { v } ( t ) . \quad \quad ( 3 9 )$$

از آنجا که در مدار DC رابطه $$I _ Q = g ( V _ Q )$$ را داریم، می‌توان نوشت:

$$\large \tilde i ( t ) = G \tilde v ( t) , \quad \quad (40)$$

که در آن،

$$\large G = \left .\frac { \mathrm { d } g } { \mathrm { d } v } \right | _ { v = V _ { Q } } . \quad \quad (41)$$

معادله (۴۰) مدل سیگنال کوچک مقاومت غیرخطی را توصیف می‌کند که به یک مقاومت خطی با رسانایی $$G$$ رابطه (۴۱) تبدیل شده است. اگر مقاومت خطی باشد، مدل سیگنال کوچک آن یک مقاومت مشابه با خودش خواهد بود.

به طور مشابه، مدل سیگنال کوچک هر منبع کنترل شده خطی یک منبع کنترل شده است.

خازن غیرخطی با معادله زیر توصیف می‌شود:

$$\large q ( t ) = c ( v ( t ) ) . \quad \quad (42)$$

اکنون، $$v ( t ) = V _ Q + \tilde v (t)$$ را جایگذاری می‌کنیم و تابع $$c ( v ( t ) )$$ را در سری تیلور حول نقطه کار قرار داده و از جملات مرتبه بالاتر صرف‌نظر می‌کنیم:

$$\large q ( t ) = c \left ( V _ { s } \right ) + \left . \frac { \mathrm { d } c } { \mathrm { d } v } \right | _ { v = V _ { Q } } \tilde { v } ( t ) . \quad \quad ( 4 3 )$$

از آنجا که

$$\large i ( t ) = \frac { \mathrm { d } q ( t ) } { \mathrm { d } t } = \tilde { i } ( t ) \quad \quad ( 44 )$$

داریم:

$$\large \tilde i ( t) = C \frac { \mathrm{d} \tilde v ( t)}{\mathrm {d } t } , \quad \quad (45)$$

که در آن،

$$\large C = \left . \frac { \mathrm { d } c } { \mathrm { d } v } \right | _ { v = V _ { Q } } . \quad \quad ( 46 )$$

معادلات (۴۵) و (۴۶) یک خازن خطی را توصیف می‌کنند که مدل سیگنال کوچک خازن غیرخطی است.

اگر خازن خطی باشد، مدل سیگنال کوچک آن یک خازن مشابه خواهد بود.

سلف غیرخطی با معادله زیر داده شده است:

$$\large \phi ( t ) = f ( i ( t ) ) . \quad \quad (47)$$

مشابه آنچه برای خازن گفتیم، مدل سیگنال کوچک سلف غیرخطی، یک سلف خطی با معادله زیر است:

$$\large \widetilde { v } ( t ) = L \frac { \mathrm { d } \tilde { i } ( t ) } { \mathrm { d } t } , \quad \quad (48)$$

که در آن،

$$\large L = \left . \frac { \mathrm { d } f } { \mathrm { d } i } \right | _ { i = I _ { Q } } . \quad \quad (49)$$

اگر سلف خطی باشد، مدل سیگنال کوچک آن یک سلف مشابه خواهد بود.

برای تشکیل مدار معادل سیگنال کوچک یک مدار، منبع DC آن را برابر صفر قرار داده و عناصرش را با مدل‌های سیگنال کوچکشان جایگزین می‌کنیم.

مدل سیگنال کوچک یک مدار غیرخطی

مدار شکل ۱۴ را همراه با روابط زیر در نظر بگیرید:

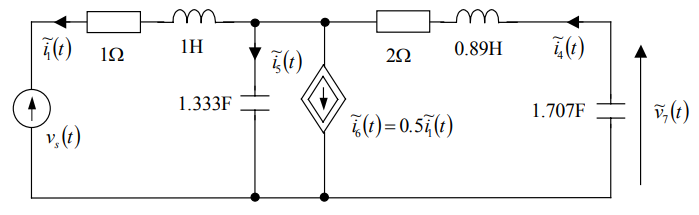
$$\large q _ 5 = v _ 5 + 0.1 v _ 5 ^ 3 , \;\; q _ 7 = 0.08 v_ 7 ^ 3 , \;\; \phi _ 4 = 0.5 e ^ {0.8 i _ 4 } .$$

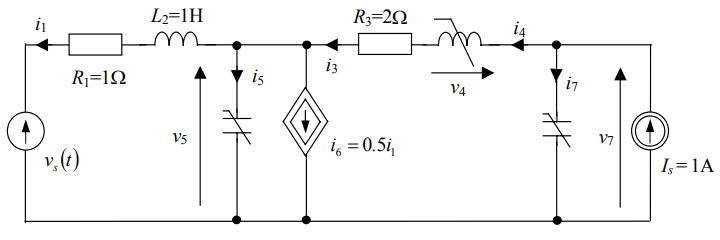
مدار معادل سیگنال کوچک حول نقطه کار را به دست آورید.

حل: ابتدا نقطه کار را پیدا می‌کنیم. بدین منظور، $$v _ s ( t)$$ را برابر با صفر قرار می‌دهیم، خازن‌ها را حذف می‌کنیم و سلف را اتصال کوتاه می‌کنیم (شکل ۱۵).

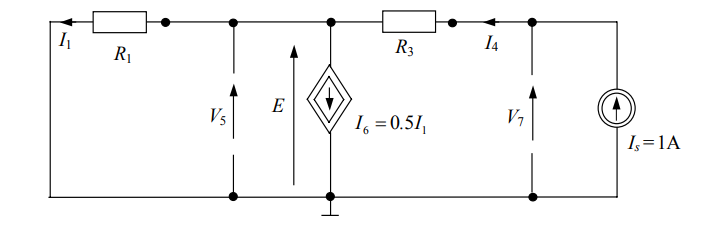
مدار را می‌توان با معادله گره توصیف کرد:

$$\large \frac { E} { 1} + 0.5 \frac {E} { 1} - 1 = 0$$

که جواب آن $$E =\frac {2}{3}\, \text{V}$$ است.

در نتیجه، خواهیم داشت:

$$\large I _ { 1 } = \frac { E } { 1 } = \frac { 2 } { 3 } \mathrm { A } , \quad I _ { 6 } = 0 . 5 I _ { 1 } = \frac { 1 } { 3 } \mathrm { A } , \quad I _ { 4 } = I _ { s } = 1 \mathrm { A } , \quad \\ \large V _ { 5 } = E = \frac { 2 } { 3 } \mathrm { V } , \quad V _ { 7 } = E + R _ { 3 } I _ { 4 } = \frac { 8 } { 3 } \mathrm { V }$$

مدل سیگنال کوچک عناصر غیرخطی مدار به صورت زیر است:

$$\large \begin {array} { l } \tilde { i } _ { 5 } ( t ) = C _ { 5 } \frac { \mathrm { d } \tilde { v } _ { 5 } ( t ) } { \mathrm { d } t } , \quad C _ { 5 } = \left . \frac { \mathrm { d } q _ { 5 } } { \mathrm { d } v _ { 5 } } \right | _ { V _ { 5 } } = 1 + 0 . 3 V _ { 5 } ^ { 2 } = 1 . 1 3 3 \mathrm { F } , \\ \tilde { i }_7 ( t ) = C _ { 7 } \frac { \mathrm { d } \tilde { v } _ { 7 } ( t ) } { \mathrm { d } t } , \quad C _ { 7 } = \left . \frac { \mathrm { d } q _ { 7 } } { \mathrm { d } v _ { 7 } } \right | _ { V _ { 7 } } = 0 . 2 4 V _ { 7 } ^ { 2 } = 1 . 7 0 7 \mathrm { F } , \\ \tilde { v } _ { 4 } ( t ) = L _ { 4 } \frac { \mathrm { d } \tilde { i } _ { 4 } ( t ) } { \mathrm { d } t } , \quad L _ { 4 } = 0 . 4 e ^ { 0 . 8 } = 0 . 8 9 \mathrm { H } . \end {array}$$

با توجه به نتایج بالا، مدار معادل سیگنال کوچک شکل ۱۶ را خواهیم داشت.

در آموزش‌های بعدی، درباره تحلیل سیگنال کوچک ترانزیستورهای BJT و FET بحث خواهیم کرد.