تابع درجه دوم – به زبان ساده

آنتن‌های خمیده، مانند آن‌هایی که در شکل زیر نشان داده شده‌اند، معمولاً برای تمرکز مایکروویوها (ریزموج‌ها) و امواج رادیویی برای انتقال سیگنال‌های تلویزیونی و تلفنی و همچنین ارتباطات ماهواره‌ای و فضاپیمایی مورد استفاده قرار می‌گیرند. سطح مقطع آنتن به شکل سهمی است که می‌توان آن را با یک تابع درجه دوم توصیف کرد.

در این آموزش از مجله فرادرس، توابع درجه دوم را بررسی خواهیم کرد که اغلب مسائل مربوط به حرکت پرتابی را مدل می‌کنند. کار با توابع درجه دوم پیچیدگی کمتری در مقایسه با توابع درجه بالاتر دارد، بنابراین فرصت خوبی برای مطالعه دقیق رفتار این توابع فراهم می‌کند.

شناخت ویژگی‌های سهمی‌ها

نمودار یک تابع درجه دوم یک منحنی U شکل به نام «سهمی» (Parabola) است. یکی از ویژگی‌های مهم نمودار این است که دارای یک نقطه «رأس» (Vertex) است. اگر سهمی به سمت بالا باز شود، رأس پایین‌ترین نقطه روی نمودار یا حداقل مقدار تابع درجه دوم (کمینه یا مینیمم) را نشان می‌دهد.

اگر سهمی به پایین باز شود، رأس بالاترین نقطه نمودار یا حداکثر مقدار تابع (بیشینه یا ماکزیمم) را نشان می‌دهد. در هر حالت، رأس یک «نقطه برگشت» (Turning Point) روی نمودار است. نمودار همچنین نسبت به خط عمودی گذرنده از رأس، متقارن است که این خط «محور تقارن» (Axis of Symmetry) سهمی نامیده می‌شود. این ویژگی‌ها در شکل زیر نشان داده شده است.

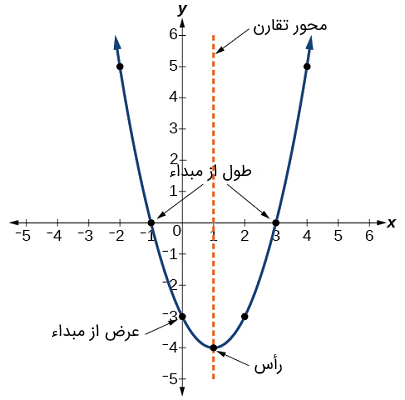
تقاطع با محور $$y$$ یا همان عرض از مبداء نقطه‌ای است که سهمی محور $$y$$ را قطع می‌کند. نقاط برخورد با محور $$x$$ یا همان طول از مبداءها نقاطی هستند که نمودار تابع محور $$x$$ را در آن‌ها قطع می‌کند. اگر طول از مبدأ وجود داشته باشد، در واقع، صفر یا ریشه تابع درجه دوم را نشان می‌دهد که همان مقادیری از $$x$$ است که در آن، $$y = 0$$ است.

مثالی از سهمی

رأس،‌ محور تقارن، صفرها و عرض از مبداء‌ سهمی شکل ۳ را مشخص کنید.

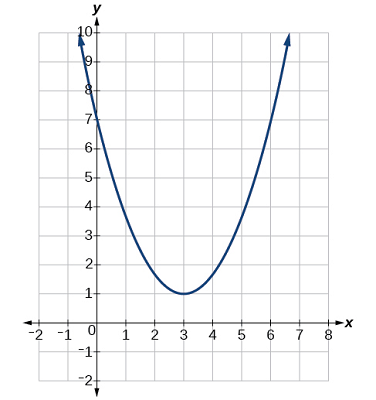
حل: رأس نقطه بازگشت تابع است. مشاهده می‌کنیم که رأس در $$( 3 ,1 )$$ قرار دارد. از آنجا که این سهمی به بالا باز شده است (تقعر آن به بالا است)، محور تقارن خط عمودی است که سهمی را در رأس قطع می‌کند. بنابراین، محور تقارن $$x = 3$$ خواهد بود. این سهمی محور $$x$$ را قطع نمی‌کند، بنابراین، صفری ندارد. همچنین، سهمی در نقطه $$( 0 , 7 )$$ محور $$y$$ را قطع می‌کند و بنابراین، عرض از مبداء دارد.

ارتباط نمودار سهمی و تابع درجه دوم آن

فرم عمومی تابع درجه دوم تابعی به شکل زیر است:

$$\large f ( x ) = a x ^ 2 + b x + c$$

فیلم آموزش شیمی ۲ – پایه یازدهم | رشته علوم تجربی و ریاضی و فیزیک در فرادرس

کلیک کنید

که در آن، $$a$$، $$b$$ و $$c$$ اعدادی حقیقی هستند و $$a \neq 0$$. اگر $$a > 0$$ باشد، سهمی به سمت بالا باز می‌شود. اگر $$a < 0$$ باشد، سهمی رو به پایین باز می‌شود. می‌توانیم از فرم عمومی سهمی برای یافتن معادله محور تقارن استفاده کنیم.

محور تقارن به صورت $$x=−\frac{b}{2a}$$ تعریف می‌شود. اگر از فرمول ریشه $$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$$ برای حل معادله $$ax^2+bx+c=0$$ به منظور تعیین طول از مبداء یا همان‌ صفرهای تابع استفاده کنیم، مقداری از $$x$$ که همواره در میانه آن‌ها، یعنی $$x=−\frac{b}{2a}$$، خواهد بود، همان معادله محور تقارن است.

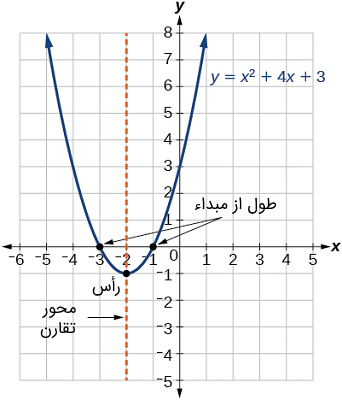
شکل ۴ نمودار تابع درجه دوم را نشان می‌دهد که به فرم عمومی $$y=x^2+4x+3$$ نوشته شده است. در این فرم، $$a = 1$$، $$b = 4$$ و $$c = 3$$ است. از آنجا که $$a > 0$$ است، سهمی رو به بالا باز می‌شود. محور تقارن نیز $$x=−\frac{4}{2(1)}=−2$$ است. این محور به صورت شهودی نیز قابل درک است،‌ زیرا با توجه به نمودار، می‌بینیم که خط عمود در $$x = - 2$$ نمودار را به دو نیمه تقسیم می‌کند. رأس همیشه روی محور تقارن قرار دارد. برای یک سهمی که رو به بالا باز شده، رأس در پایین‌ترین نقطه روی منحنی، یعنی $$( - 2 , - 1 )$$ قرار دارد. طول از مبداءها نقاطی هستند که سهمی محور $$x$$ را در آنجا قطع می‌کند و در این مثال، در $$( - 3 , 0 )$$ و $$( - 1 , 0 )$$ قرار دارند.

فرم استاندارد تابع درجه دوم تابع را به صورت زیر نشان می‌دهد:

$$\large f ( x ) = a ( x − h ) ^ 2 + k$$

که $$( h , k )$$ رأس آن است. از آنجا که رأس در فرم استاندارد تابع درجه دوم ظاهر می‌شود، به فرم رأس تابع درجه دوم نیز مشهور است.

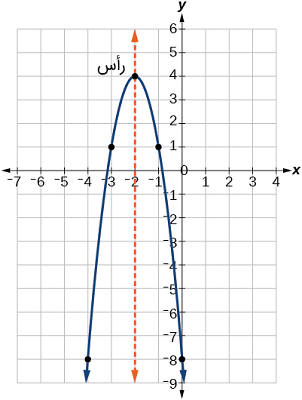
با توجه به فرم استاندارد، اگر $$a > 0$$ باشد، سهمی رو به بالا باز می‌شود و رأس در نقطه کمینه قرار خواهد داشت. اگر $$a < 0$$ باشد، سهمی رو به پایین باز شده و رأس نقطه بیشینه خواهد بود. شکل ۵ نمودار تابع درجه دوم را نشان می‌دهد که به فرم استاندارد به صورت $$y=−3(x+2)^2+4$$ نوشته شده است. از آنجا که در این مثال، $$x - h = x + 2$$ است، $$h = - 2$$ خواهد بود. در این فرم، $$a =- 3$$، $$h = - 2$$ و $$k = 4$$ است. به دلیل آنکه $$a < 0$$ است، سهمی رو به پایین باز می‌شود. رأس در $$( - 2 , 4 )$$ قرار دارد.

فرم استاندارد برای تعیین چگونگی تبدیل منحنی از $$y = x ^ 2$$ مفید است. شکل ۶ نمودار تابع پایه $$X ^ 2$$ را نشان می‌دهد.

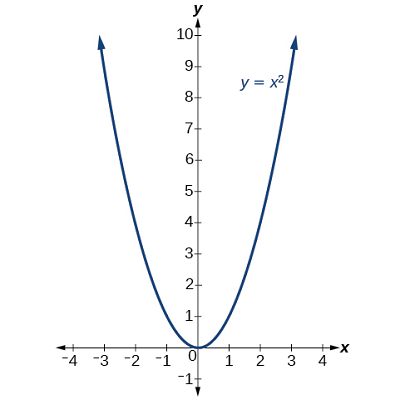
اگر $$k > 0$$ باشد، نمودار به سمت بالا جابه‌جا می‌شود و اگر $$k < 0$$ باشد، نمودار به سمت پایین جابه‌جا خواهد شد. در شکل ۵، $$k > 0$$ است، بنابراین، نمودار به اندازه ۴ واحد به بالا جابه‌جا شده است. اگر $$h > 0$$ باشد، نمودار به راست جابه‌جا می‌شود، و اگر $$h < 0$$ باشد، نمودار به چپ جابه‌جا خواهد شد. در شکل ۵، $$h < 0$$ است، بنابراین، نمودار به اندازه ۲ واحد به چپ جابه‌جا شده است.

اندازه $$a$$، کشیدگی نمودار را مشخص می‌کند. اگر $$|a|>1$$ باشد، نقطه متناظر با یک مقدار مشخص $$x$$ از محور $$x$$ دورتر می‌شود، بنابراین، نمودار نازک‌تر می‌شود و یک کشیدگی عمودی وجود خواهد داشت. اگر $$|a|<1$$ باشد، نقطه متناظر با یک مقدار مشخص $$x$$، به محور $$x$$ نزدیک‌تر می‌شود، بنابراین، نمودار بازتر خواهد شد. در شکل ۵، $$|a|>1$$ است و بنابراین، نمودار جمع‌تر می‌شود.

فرم استاندارد و فرم عمومی روش‌های یکسانی برای توصیف تابع هستند. با بسط فرم عمومی و برابر قرار دادن آن با فرم استاندارد، می‌توان این مورد را مشاهده کرد.

$$\large \begin {align*} a ( x − h ) ^ 2 + k & = a x ^ 2 + b x + c \\[4pt] a x ^ 2 − 2 a h x + ( a h ^ 2 + k ) & = a x ^ 2 + b x + c \end {align*}$$

اکنون ضرایب جملات باید برابر باشند:

$$\large – 2 a h = b \text {} \; \ \Rightarrow \; \; h = − \dfrac { b } { 2 a } . \nonumber$$

این همان محور تقارن است که پیش‌تر آن را تعریف کردیم. با برابر قرار دادن جملات ثابت، خواهیم داشت:

$$\large \begin {align*} a h ^ 2 + k & = c \\ k & = c − a h ^ 2 \\ & = c − a − \Big ( \dfrac { b } { 2 a } \Big ) ^ 2 \\ & = c − \dfrac { b ^ 2 } { 4 a } \end {align*}$$

اگرچه، در عمل، معمولاً ساده‌تر این است که به یاد داشته باشیم $$k$$ مقدار خروجی تابع به ازای ورودی $$h$$ است، به عبارت دیگر، $$f ( h ) = k$$ است.

پس به طور خلاصه، می‌توان گفت:

• فرم عمومی یک تابع درجه دوم $$f(x)=ax^2+bx+c$$ است که $$a$$، $$b$$ و $$c$$ اعدادی حقیقی هستند و $$a \neq 0$$.
• فرم استاندارد یک تابع درجه دوم $$f(x)=a(x−h)^2+k$$ است.
• رأس $$( h , k )$$ در مختصات زیر واقع شده است:

$$\large h = – \dfrac { b } { 2 a } , \; k = f ( h ) = f ( \dfrac { − b } { 2 a } ) .$$

نوشتن فرم عمومی تابع درجه دوم

برای اینکه یک تابع درجه دوم را به فرم عمومی بنویسیم، کارهای زیر را انجام می‌دهیم:

1. جابه‌جایی افقی سهمی را مشخص کنید؛‌ این مقدار $$h$$ است. جابه‌جایی عمودی سهمی را تعیین کنید؛ این مقدار $$k$$ است.
2. مقادیر جابه‌جایی افقی و عمودی را برای $$h$$ و $$k$$ در تابع $$f(x)=a(x–h)^2+k$$ جایگذاری کنید.
3. مقادیر هر نقطه علاوه بر رأس را روی نمودار سهمی برای $$x$$ و $$f ( x )$$ جایگذاری کنید.
4. ضریب کشیدگی $$|a|$$ را به دست آورید.
5. اگر سهمی به بالا باز شود، $$a > 0$$ خواهد بود. اگر سهمی به سمت پایین باز شود، $$a < 0$$ است، زیرا این بدین معنی است که نمودار حول محور $$x$$ بازتاب دارد.
6. معادله را گسترش داده و آن را برای به دست آوردن فرم عمومی ساده کنید.

مثال فرم عمومی تابع درجه دوم

معادله تابع درجه دوم $$g$$ مربوط به شکل ۷ را با تغییر $$f(x)=x^2$$ بنویسید و جملات را برای نوشتن معادله به فرم عمومی ساده کنید.

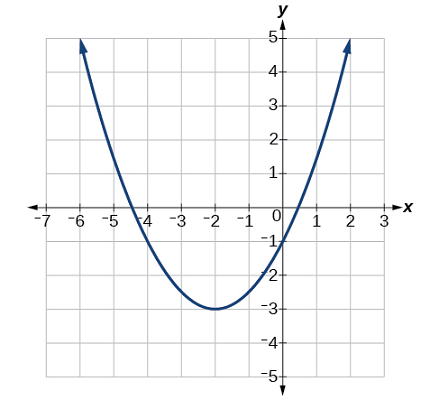
حل: مشاهده می‌کنیم که $$g$$ نمودار $$f(x)=x^2$$ است که ۲ واحد به چپ و ۳ واحد به پایین جابه‌جا شده و فرمول آن $$g(x)=a(x+2)^2–3$$ خواهد بود.

با جایگذاری مختصات یک نقطه ماننده $$(0,−1)$$ در منحنی، می‌توانیم ضریب کشیدگی را محاسبه کنیم:

$$\large \begin {align} − 1 & = a ( 0 + 2 ) ^ 2 − 3 \\ 2 & = 4 a \\ a & = \dfrac { 1 } { 2 } \end {align}$$

مدل جبری این نمودار به فرم استاندارد $$g(x)=\dfrac{1}{2}(x+2)^2–3$$ است.

برای نوشتن آن به فرم چندجمله‌ای عمومی، می‌توانیم فرمول را بسط داده و جملات را ساده کنیم:

$$\large \begin {align} g ( x ) & = \dfrac { 1 } { 2 } ( x + 2 ) ^ 2 − 3 \\ & = \dfrac { 1 } { 2 } ( x + 2 ) ( x + 2 ) − 3 \\ & = \dfrac { 1 } { 2 } ( x ^ 2 + 4 x + 4 ) − 3 \\ & = \dfrac { 1 }{ 2 } x ^ 2 +2 x + 2 − 3 \\ & = \dfrac { 1 } { 2 } x ^ 2 + 2 x − 1 \end {align}$$

محاسبه رأس سهمی با فرم استاندارد

برای به دست آوردن رأس سهمی از تابع درجه دوم به فرم استاندارد گام‌های زیر را طی می‌کنیم:

1. $$a$$، $$b$$ و $$c$$ را مشخص کنیم.
2. $$h$$ (مختصات $$x$$ رأس) را با جایگذاری $$a$$ و $$b$$ در $$h=–\frac{b}{2a}$$ بیابید.
3. $$k$$ (مختصات $$y$$ رأس) را با محاسبه $$k=f(h)=f\Big(−\frac{b}{2a}\Big)$$ به دست آورید.

مثال محاسبه رأس سهمی با فرم استاندارد

رأس تابع درجه دوم $$f(x)=2x^2–6x+7$$ را بیابید. درجه دوم را در فرم استاندارد (فرم رأس) بازنویسی کنید.

حل: مختصه افقی رأس به صورت زیر خواهد بود:

$$\large \begin {align} h & = – \dfrac { b } { 2 a } \\ & = - \dfrac { - 6 } { 2 ( 2 ) } \\ & = \dfrac { 6 } { 4 } \\ & = \dfrac { 3 }{ 2 } \end {align}$$

مختصه عمودی رأس به شکل زیر است:

$$\large \begin {align} k & = f ( h ) \\ & = f \Big ( \dfrac { 3 }{ 2 } \Big ) \\ & = 2 \Big ( \dfrac { 3 } { 2 } \Big ) ^ 2 − 6 \Big ( \dfrac { 3 } { 2 } \Big ) + 7 \\ & = \dfrac { 5 } { 2 } \end {align}$$

با بازنویسی در فرم استاندارد، ضریب کشیدگی همان $$a$$ در تابع درجه دوم اصلی خواهد بود.

$$\large \begin {align*} f ( x ) & = a x ^ 2 + b x + c \\ f ( x ) & = 2 x ^ 2 − 6 x + 7 \end {align*}$$

با استفاده از رأس برای تعیین جابه‌جایی، داریم:

$$\large f ( x ) = 2 \Big ( x – \dfrac { 3 } { 2 } \Big ) ^ 2 + \dfrac { 5 } { 2 }$$

یکی از دلایلی که می‌خواهیم رأس سهمی را مشخص کنیم، این است که این نقطه به ما مقدار ماکزیمم و مینیمم تابع ($$k$$) و جایی که رخ می‌دهد ($$h$$) را خواهد داد.

دامنه و برد تابع درجه دوم

هر عددی می‌تواند به عنوان مقدار ورودی یک تابع درجه دوم باشد. بنابراین، دامنه هر تابع درجه دوم همه اعداد حقیقی است.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

از آنجا که سهمی‌ها یک نقطه بیشینه یا یک نقطه کمینه دارند، برد آن‌ها محدود است. به دلیل آنکه رأس یک سهمی مینیمم یا ماکزیمم است، برد شامل همه $$y$$های بزرگ‌تر یا مساوی مختصه $$y$$ در نقطه برگشت یا کوچک‌تر یا مساوی آن است (بسته به اینکه سهمی به بالا باز شود یا به پایین).

برد یک تابع درجه دوم که به فرم عمومی $$f(x)=ax^2+bx+c$$ نوشته شده و در آن، $$a > 0$$ است، برابر با $$f(x){\geq}f ( −\frac{b}{2a}\Big)$$ یا $$[ f(−\frac{b}{2a}),∞ )$$ خواهد بود. همچنین، اگر $$a < 0$$ باشد، برد تابع $$f(x) \leq f(−\frac{b}{2a})$$ یا $$(−∞,f(−\frac{b}{2a})]$$ است.

برد تابع درجه دوم به فرم استاندارد $$f(x)=a(x−h)^2+k$$ و $$a > 0$$ برابر با $$f(x) \geq k$$ و برای $$a < 0$$ در محدوده $$f(x) \leq k$$ است.

اگر یک تابع درج دوم را در اختیار داشته باشیم، برای به دست آوردن دامنه و برد آن، کارهای گام‌های زیر را انجام می‌دهیم:

1. تابع، هرچه که باشد، دامنه‌اش تمام اعداد حقیقی خواهد بود.
2. مثبت یا منفی بودن $$a$$ را مشخص کنید. اگر $$a$$ مثبت باشد، سهمی دارای مینیمم است و اگر منفی باشد، یک ماکزیمم خواهد داشت.
3. مقدار مینیمم یا ماکزیمم تابع ($$k$$) را به دست آورید.
4. اگر سهمی مینیمم دارد، برد تابع $$f(x){\geq}k$$ یا $$\left[k,\infty\right)$$ است. اگر سهمی داری ماکزیمم باشد، برد تابع $$f(x){\leq}k$$ یا $$\left(−\infty,k\right]$$ قخواهد بود.

مثال دامنه و برد تابع درجه دوم

دامنه و برد تابع $$f(x)=−5x^2+9x−1$$ را مشخص کنید.

حل: همان‌طور که پیش‌تر گفتیم، دامنه این تابع همه اعداد حقیقی است.

از آنجا که $$a$$ منفی است، سهمی به پایین باز می‌شود و دارای یک مقدار ماکزیمم خواهد بود. باید این مقدار ماکزیمم را تعیین کنیم. بدین منظور، می‌توانیم مقدار $$x$$ رأس را محاسبه کنیم:

$$\large \begin {align} h & = − \dfrac { b } { 2 a } \\ & = −\dfrac { 9 } { 2 ( - 5 ) } \\ & = \dfrac { 9 } { 1 0 } \end {align}$$

مقدار ماکزیمم با محاسبه $$f ( h )$$ محاسبه می‌شود:

$$\large \begin {align} f ( \dfrac { 9 } { 1 0 } ) & = 5 ( \dfrac { 9 } { 1 0 } ) ^ 2 + 9 ( \dfrac { 9 } { 1 0 } ) - 1 \\ & = \dfrac { 6 1 } { 2 0 } \end {align}$$

بنابراین، برد تابع $$f(x){\leq}\frac{61}{20}$$ یا $$\left(−\infty,\frac{61}{20}\right]$$ است.

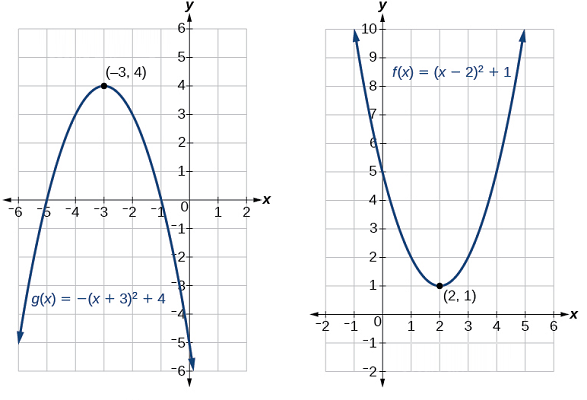
ماکزیمم و مینیمم تابع درجه دوم

خروجی تابع درجه دوم در رأس، همان مقدار مینیمم یا ماکزیمم تابع، بسته به تقعر سهمی، است. شکل زیر این موضوع را به خوبی نشان می‌دهد.

محاسبه عرض از مبداء و طول از مبداء تابع درجه دوم

گاهی در برخی موارد لازم است مقدار عرض از مبداء و طول از مبداء تابع درجه دوم را به دست آوریم. بدین منظور، کافی است کارهای زیر را انجام دهیم:

1. برای به دست آوردن عرض از مبداء $$f ( 0 )$$ را به دست آورید.
2. برای به دست آوردن طول از مبداء معادله درجه دوم $$f ( x ) = 0$$ را حل کنید.

مثال عرض از مبداء و طول از مبداء تابع درجه دوم

عرض از مبداء و طول از مبداء تابع درجه دوم $$f(x)=3x^2+5x−2$$ را به دست آورید.

حل: عرض از مبداء را با محاسبه $$f ( 0 )$$ به دست می‌آوریم:

$$\large \begin {align} f ( 0 ) & = 3 ( 0 ) ^ 2 + 5 ( 0 ) − 2 \\ & = − 2 \end {align}$$

بنابراین، عرض از مبداء در $$(0,−2)$$ قرار دارد.

برای محاسبه طول از مبداءها نیز کافی است معادله $$f ( x ) = 0$$ را حل کنیم.

$$\large 0=3x^2+5x−2$$

این معادله را می‌توان به صورت زیر نوشت:

$$\large 0=(3x−1)(x+2)$$

بنابراین، طول از مبداءها $$(\frac{1}{3},0)$$ و $$(−2,0)$$ هستند.

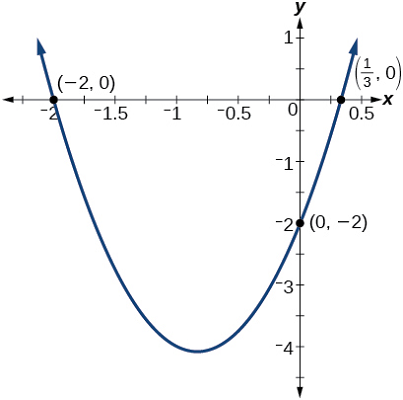
شکل بالا عرض از مبداء و طول از مبداء را به خوبی نشان می‌دهد.

جمع‌بندی

در این مطلب از مجله فرادرس با تابع درجه دوم آشنا شدیم. تابع درجه دوم را به نام سهمی‌ها نیز می‌شناسیم. سهمی ویژگی‌های مهمی دارند که به هنگام رسم نمودار آن‌ها باید به این ویژگی‌ها توجه کنیم.