تابع جزء صحیح — به زبان ساده

پیش‌تر، در مجموعه آموزش‌های ریاضیات مجله فرادرس، توابعی مانند قدر مطلق، نمایی، هذلولوی و... را معرفی کردیم. در ادامه این سلسله آموزش‌ها، تابع جزء صحیح را معرفی می‌کنیم.

جزء صحیح چیست؟

ابتدا به چند جمله زیر توجه کنید:

• جزء صحیح عدد $$2.35$$، عدد $$2$$ است.
• جزء صحیح عدد $$-4.36$$، عدد $$-5$$ است.
• جزء صحیح عدد $$-1$$، عدد $$-1$$ است.

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

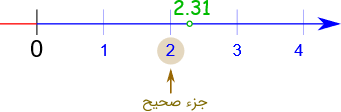
ویژگی مشترک سه عبارت بالا چیست؟ همان‌طور که شما هم پی برده‌اید، برای نوشتن جزء صحیح یک عدد، نزدیک‌ترین عدد صحیح کوچک‌تر یا مساوی با آن را نوشته‌ایم. در حقیقت می‌توان گفت، عبارت جزء صحیح یک عدد، معادل عبارت نزدیک‌ترین عدد صحیح کوچک‌تر یا مساوی با آن عدد است. برای تعریف جزء صحیح، معمولاً عبارت‌ بزرگ‌ترین عدد صحیح کوچک‌تر یا مساوی را نیز به‌کار می‌برند. توابع جزء صحیح را «تابع کف» (Floor Function) نیز می‌نامند. در شکل زیر، جزء صحیح عدد $$2.31$$ روی محور نشان داده شده است.

در جدول زیر، جزء صحیح چند عدد نوشته شده است.

نمادهای جزء صحیح یا تابع جزء صحیح یک عدد را با براکت ناقص نیز نشان می‌دهند.

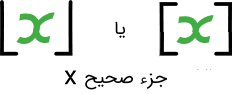
تا دهه 1970 معمولاً از براکت ([ ]) کامل برای نشان دادن جزء صحیح استفاده می‌شد و پس از آن، براکت ناقص ($$\lfloor \, \rfloor$$) به‌کار رفت. البته هنوز هم براکت کامل برای نمایش تابع جزء صحیح مورد استفاده قرار می‌گیرد.

در ادامه، تعریف رسمی جزء صحیح را بیان می‌کنیم.

تعریف تابع جزء صحیح

تابع جزء صحیح، بر مبنای همان مفهوم جزء صحیح تعریف می‌شود که در بالا بیان کردیم. تابع جزء صحیح $$x$$ را معمولاً با نماد $$y=[x]$$ نشان می‌دهند. به همین دلیل، آن را تابع براکت نیز می‌نامند. سه تعریف ریاضی این تابع، به‌صورت زیر است:

ابتدا فرض کنید $$x$$ یک عدد حقیقی باشد، آن‌گاه:

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

تعریف ۱: جزء صحیح متغیر $$x$$، سوپریمم مجموعه اعداد صحیحی است که از $$x$$ بزرگ‌تر نیستند. به عبارت دیگر:

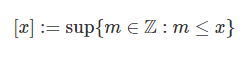
تعریف ۲: جزء صحیح عدد حقیقی $$x$$، بزرگ‌ترین عضو مجموعه اعداد صحیح زیر است:

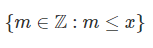
تعریف ۳: جزء صحیح $$x$$، عدد صحیح منحصر به فرد $$[x]$$ است که در رابطه زیر صدق می‌کند:

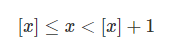
خواص تابع جزء صحیح

در این بخش، چند مورد از مهم‌ترین خواص توابع جزء صحیح را بیان می‌کنیم. با استفاده از تعاریفی که بیان کردیم، به‌راحتی می‌توان این ویژگی‌ها را اثبات کرد.

فرض کنید $$[x]=a$$ (که $$a$$ یک عدد صحیح است)، آن‌گاه داریم:

1.  $$[x]=a$$ اگر و تنها اگر $$a \le x < a+1$$
2.  $$[x]=a$$ اگر و تنها اگر $$x-1$$
3.  $$[x]$$ اگر و تنها اگر $$x$$
4.  $$a \le [x]$$ اگر و تنها اگر $$a \le x$$
5.  $$[x+a]=[x]+a$$
6.  $$[x]+[y]\le [x+y] \le [x]+[y]+1$$

معادلات توابع جزء صحیح

معادلات شامل توابع جزء صحیح را می‌توان با توجه به تعاریف و خواصی که بیان شد، به‌سادگی حل کرد. برای آشنایی بیشتر، یک مثال را بررسی می‌کنیم.

مثال

معادله زیر را حل کنید:

$$[0.5+[x]]=20$$

حل: ابتدا فرض می‌کنیم $$[x]=y$$. در نتیجه، داریم:

$$[0.5+y]=20$$

طبق تعریف تابع جزء صحیح، رابطه بالا، معادل با نامساوی زیر است:

$$20 \le y+0.5<21$$

یا

$$19.5 \le y <20.5$$

از آن‌جایی که $$y$$ برابر با جزء صحیح $$x$$ است، باید یک عدد صحیح باشد. بنابراین، داریم:

$$y=20=[x]$$

در نتیجه، پاسخ $$x$$ به‌صورت زیر خواهد بود:

$$20 \le x <21$$

نمودار تابع جزء صحیح

ابتدا از ساده‌ترین تابع جزء صحیح، یعنی $$y=[x]$$ شروع می‌کنیم. اگر به تعریف تابع جزء صحیح دقت کنیم، می‌توانیم حدس بزنیم که نمودار مربوط به این تابع، به صورت بازه ای خواهد بود. جدول زیر، این موضوع را به خوبی نشان می‌دهد:

نمودار مربوط به جدول بالا به صورت زیر خواهد بود:

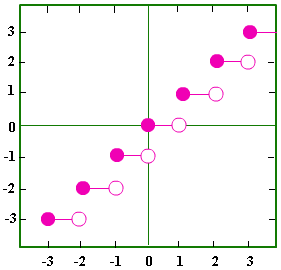
به‌دلیل شکل خاص نمودار جزء صحیح، آن را پلکانی یا پله‌ای می‌نامند.

مثال

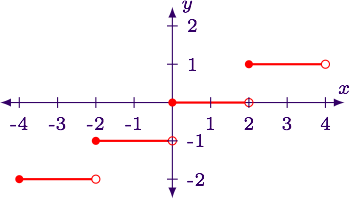
نمودار تابع $$y=[\frac{1}{2}x]$$ را رسم کنید.

حل: برای رسم توابع جز صحیح، آن‌ها را به‌صورت بازه‌ای بررسی می‌کنیم. برای رسم نمودار مربوط به این مثال، ابتدا جدول زیر را تشکیل می‌دهیم که شامل بازه‌های مختلف $$x$$ است.

با توجه به سه بازه نمونه که انتخاب و بررسی کردیم، نمودار مربوط به تابع جز صحیح، به صورت زیر خواهد بود:

جمع‌بندی

در این مطلب از مجله فرادرس با مفهوم جزء صحیح و توابع جزء صحیح آشنا شدیم. این توابع یکی از بخش‌های مهم در ریاضیات دبیرستان و دانشگاهی است.