در آموزشهای قبلی مجله فرادرس ، مفاهیم مربوط به انتگرال دوگانه و نحوه محاسبه آن را در دستگاه مختصات کارتزین بیان کردیم. در این آموزش، با ارائه مثالهای مختلف، نحوه محاسبه انتگرال دوگانه در مختصات قطبی را بیان خواهیم کرد. پیشنهاد میکنیم برای آشنایی بیشتر با مفاهیم پایه این آموزش، مباحث انتگرال دوگانه و مختصات قطبی را مطالعه کنید.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
همانطور که در آموزش مربوط به انتگرال دوگانه گفتیم، انتگرال دوگانه تابع f f f R R R
که در آن، d A dA d A f f f R R R ( r , θ ) (r, \theta) ( r , θ ) d A dA d A
توجه کنید که متغیر r r r d A = d x d y dA=dxdy d A = d x d y
شاید این پرسش پیش آید که رابطه بالا چگونه بهدست آمده است. در ادامه، نحوه رسیدن به فرمول مورد نظر را بیان میکنیم. همانگونه که میدانیم، یکی از حالتهای خاص تغییر متغیر، تبدیل از دستگاه مختصات کارتزین به دستگاه مختصات قطبی است:
x = r cos θ , y = r sin θ . \large x = r\cos \theta ,\;\;y = r\sin \theta . x = r cos θ , y = r sin θ .
دترمینان ماتریس ژاکوبی، یکی از ابزارهای تبدیل مختصات چندگانه است. با استفاده از دترمینان این ماتریس، میخواهیم رابطه بین d A dA d A
$$\large {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {r,\theta } \right)}} }<br />
= {\left| {\begin{array}{*{20}{c}}<br />
{\frac{{\partial x}}{{\partial r}}}&{\frac{{\partial x}}{{\partial \theta }}}\\<br />
{\frac{{\partial y}}{{\partial r}}}&{\frac{{\partial y}}{{\partial \theta }}}<br />
\end{array}} \right| } \\ \large<br />
= {\left| {\begin{array}{*{20}{c}}<br />
{\frac{{\partial \left( {r\cos \theta } \right)}}{{\partial r}}}&{\frac{{\partial \left( {r\cos \theta } \right)}}{{\partial \theta }}}\\<br />
{\frac{{\partial \left( {r\sin \theta } \right)}}{{\partial r}}}&{\frac{{\partial \left( {r\sin \theta } \right)}}{{\partial \theta }}}<br />
\end{array}} \right| }<br />
= {\left| {\begin{array}{*{20}{c}}<br />
{\cos \theta }&{ – r\sin \theta }\\<br />
{\sin\theta }&{r\cos \theta }<br />
\end{array}} \right| } \\ \large<br />
= {\cos \theta \cdot r\cos \theta }-{ \left( { – r\sin \theta } \right) \cdot \sin \theta } \\ \large<br />
= {r\,{\cos ^2}\theta + r\,{\sin ^2}\theta }<br />
= {r\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right) }={ r.} $$
در نتیجه، دیفرانسیل در دستگاه مختصات قطبی، بهصورت زیر است:
d x d y = ∣ ∂ ( x , y ) ∂ ( r , θ ) ∣ d r d θ = r d r d θ . \large {dxdy }={ \left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {r,\theta } \right)}}} \right|drd\theta } = {rdrd\theta .} d x d y = ∂ ( r , θ ) ∂ ( x , y ) d r d θ = r d r d θ .
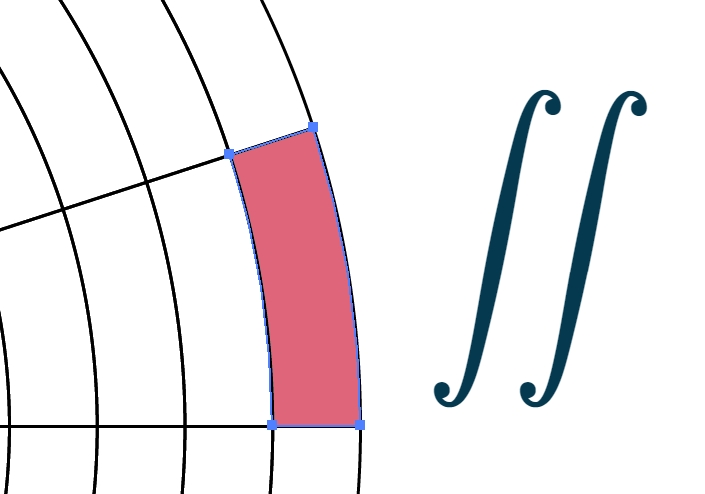
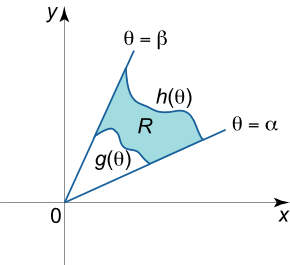
اکنون ناحیه R R R
0 ≤ g ( θ ) ≤ r ≤ h ( θ ) , α ≤ θ ≤ β , β – α ≤ 2 π . \large{0 \le g\left( \theta \right) \le r \le h\left( \theta \right),\;\;}\kern-0.3pt {\alpha \le \theta \le \beta ,\;\;}\kern-0.3pt {\;\;\beta – \alpha \le 2\pi .} 0 ≤ g ( θ ) ≤ r ≤ h ( θ ) , α ≤ θ ≤ β , β – α ≤ 2 π .
بنابراین، انتگرال دوگانه در مختصات قطبی را میتوان با فرمول زیر بیان کرد:
∬ R f ( x , y ) d x d y = ∫ α β ∫ g ( θ ) h ( θ ) f ( r cos θ , r sin θ ) r d r d θ \large {\iint\limits_R {f\left( {x,y} \right)dxdy} } = {\int\limits_\alpha ^\beta {\int\limits_{g\left( \theta \right)}^{h\left( \theta \right)} {f\left( {r\cos \theta ,r\sin \theta } \right)rdrd\theta } } } R ∬ f ( x , y ) d x d y = α ∫ β g ( θ ) ∫ h ( θ ) f ( r cos θ , r sin θ ) r d r d θ
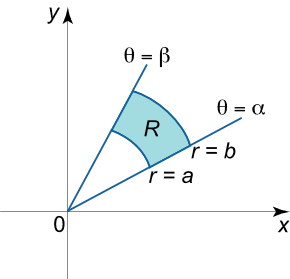
ناحیه انتگرالگیری، مستطیل قطبی نام دارد و در شرایط زیر صدق میکند:
0 ≤ a ≤ r ≤ b , α ≤ θ ≤ β , β – α ≤ 2 π . \large {0 \le a \le r \le b,\;\;}\kern-0.3pt {\alpha \le \theta \le \beta ,\;\;}\kern-0.3pt {\;\;\beta – \alpha \le 2\pi .} 0 ≤ a ≤ r ≤ b , α ≤ θ ≤ β , β – α ≤ 2 π .
در این حالت، فرمول تغییر متغیر را میتوان بهصورت زیر نوشت:
∬ R f ( x , y ) d x d y = ∫ α β ∫ a b f ( r cos θ , r sin θ ) r d r d θ . \large {\iint\limits_R {f\left( {x,y} \right)dxdy} } = {\int\limits_\alpha ^\beta {\int\limits_{a}^{b} {f\left( {r\cos \theta ,r\sin \theta } \right)rdrd\theta } } .} R ∬ f ( x , y ) d x d y = α ∫ β a ∫ b f ( r cos θ , r sin θ ) r d r d θ .
توجه داشته باشید که ضریب r r r
مثالهایی از انتگرال دوگانه در مختصات قطبی
در ادامه، مثالهایی بیان میشود که روش انتگرالگیری دوگانه را در مختصات قطبی بهخوبی نشان میدهند.
مثال ۱
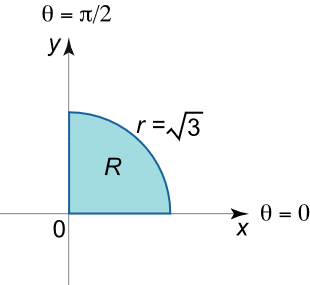
انتگرال دوگانه ∬ R ( x 2 + y 2 ) d y d x \iint\limits_R {\left( {{x^2} + {y^2}} \right)dydx} R ∬ ( x 2 + y 2 ) d y d x R R R 0 ≤ θ ≤ π 2 0 \le \theta \le {\large\frac{\pi }{2}\normalsize} 0 ≤ θ ≤ 2 π r = 3 r = \sqrt 3 r = 3
حل: ناحیه R R R
R = { ( r , θ ) ∣ 0 ≤ r ≤ 3 , 0 ≤ θ ≤ π 2 } \large {R }={ \Big\{ {\left( {r,\theta } \right)|\;0 \le r \le \sqrt 3 ,\; }}\kern0pt{{ 0 \le \theta \le {\frac{\pi }{2}}} \Big\} } R = { ( r , θ ) ∣ 0 ≤ r ≤ 3 , 0 ≤ θ ≤ 2 π }
با استفاده از فرمولِ
∬ R f ( x , y ) d x d y = ∫ α β ∫ a b f ( r cos θ , r sin θ ) r d r d θ , \large {\iint\limits_R {f\left( {x,y} \right)dxdy} } = {\int\limits_\alpha ^\beta {\int\limits_{a}^{b} {f\left( {r\cos \theta ,r\sin \theta } \right)rdrd\theta } },} R ∬ f ( x , y ) d x d y = α ∫ β a ∫ b f ( r cos θ , r sin θ ) r d r d θ ,
میتوان نوشت:
∬ R ( x 2 + y 2 ) d y d x = ∫ 0 π 2 ∫ 0 3 r 2 ( cos 2 θ + sin 2 θ ) r d r d θ = ∫ 0 π 2 d θ ∫ 0 3 r 3 d r = θ ∣ 0 π 2 ⋅ ( r 4 4 ) ∣ 0 3 = π 2 ⋅ 9 4 = 9 π 8 . \large{\iint\limits_R {\left( {{x^2} + {y^2}} \right)dydx} } = {\int\limits_0^{\frac{\pi }{2}} {\int\limits_0^{\sqrt 3 } {{r^2}\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right)rdrd\theta } } } \\ \large = {\int\limits_0^{\frac{\pi }{2}} {d\theta } \int\limits_0^{\sqrt 3 } {{r^3}dr} } = {\left. \theta \right|_0^{\frac{\pi }{2}} \cdot \left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^{\sqrt 3 } } = {\frac{\pi }{2} \cdot \frac{9}{4} }={ \frac{{9\pi }}{8}.} R ∬ ( x 2 + y 2 ) d y d x = 0 ∫ 2 π 0 ∫ 3 r 2 ( cos 2 θ + sin 2 θ ) r d r d θ = 0 ∫ 2 π d θ 0 ∫ 3 r 3 d r = θ ∣ 0 2 π ⋅ ( 4 r 4 ) 0 3 = 2 π ⋅ 4 9 = 8 9 π .
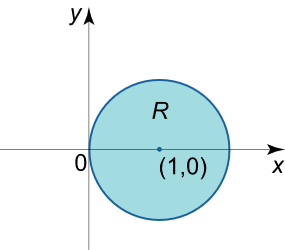
مثال ۲
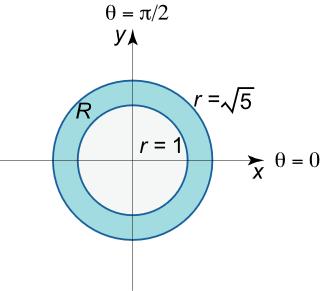
انتگرال ∬ R x y d y d x \iint\limits_R {xydydx} R ∬ x y d y d x R R R x 2 + y 2 = 1 {x^2} + {y^2} = 1 x 2 + y 2 = 1 x 2 + y 2 = 5 {x^2} + {y^2} = 5 x 2 + y 2 = 5
حل: ناحیه انتگرالگیری R R R
R = { ( r , θ ) ∣ 1 ≤ r ≤ 5 , 0 ≤ θ ≤ 2 π } . \large {R }={ \left\{ {\left( {r,\theta } \right)|\;1 \le r \le \sqrt 5 ,\;}\right.}\kern0pt {\left.{ 0 \le \theta \le 2\pi } \right\}.} R = { ( r , θ ) ∣ 1 ≤ r ≤ 5 , 0 ≤ θ ≤ 2 π } .
بنابراین، از فرمول زیر استفاده میکنیم:
∬ R f ( x , y ) d x d y = ∫ α β ∫ a b f ( r cos θ , r sin θ ) r d r d θ \large {\iint\limits_R {f\left( {x,y} \right)dxdy} } = {\int\limits_\alpha ^\beta {\int\limits_{a}^{b} {f\left( {r\cos \theta ,r\sin \theta } \right)rdrd\theta } }} R ∬ f ( x , y ) d x d y = α ∫ β a ∫ b f ( r cos θ , r sin θ ) r d r d θ
در نتیجه، انتگرال بهصورت زیر قابل محاسبه است:
∬ R x y d y d x = ∫ 0 2 π ∫ 1 5 r cos θ r sin θ r d r d θ = ∫ 0 2 π sin θ cos θ d θ ∫ 1 5 r 3 d r = 1 2 ∫ 0 2 π sin 2 θ d θ ∫ 1 5 r 3 d r = 1 2 ( – cos 2 θ 2 ) ∣ 0 2 π ⋅ ( r 4 4 ) ∣ 1 5 = 1 4 ( – cos 4 π + cos 0 ) ⋅ 1 4 ( 25 – 1 ) = 1 4 ( – 1 + 1 ) ⋅ 6 = 0. \large {\iint\limits_R {xydydx} } = {\int\limits_0^{2\pi } {\int\limits_1^{\sqrt 5 } {r\cos \theta r\sin \theta rdrd\theta } } } \\ \large = {\int\limits_0^{2\pi } {\sin \theta \cos \theta d\theta } \int\limits_1^{\sqrt 5 } {{r^3}dr} } = {\frac{1}{2}\int\limits_0^{2\pi } {\sin 2\theta d\theta } \int\limits_1^{\sqrt 5 } {{r^3}dr} } \\ \large = {\frac{1}{2}\left. {\left( { – \frac{{\cos 2\theta }}{2}} \right)} \right|_0^{2\pi } \cdot \left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_1^{\sqrt 5 } } = {\frac{1}{4}\left( { – \cos 4\pi + \cos 0} \right) \cdot \frac{1}{4}\left( {25 – 1} \right) } = {\frac{1}{4}\left( { – 1 + 1} \right) \cdot 6 }={ 0.} R ∬ x y d y d x = 0 ∫ 2 π 1 ∫ 5 r cos θ r sin θ r d r d θ = 0 ∫ 2 π sin θ cos θ d θ 1 ∫ 5 r 3 d r = 2 1 0 ∫ 2 π sin 2 θ d θ 1 ∫ 5 r 3 d r = 2 1 ( – 2 cos 2 θ ) 0 2 π ⋅ ( 4 r 4 ) 1 5 = 4 1 ( – cos 4 π + cos 0 ) ⋅ 4 1 ( 25–1 ) = 4 1 ( –1 + 1 ) ⋅ 6 = 0.
مثال ۳
انتگرال دوگانه ∬ R sin θ d r d θ \iint\limits_R {\sin \theta drd\theta } R ∬ sin θ d r d θ R R R r = 1 + cos θ r = 1 + \cos \theta r = 1 + cos θ
حل: در مختصات قطبی، انتگرال را میتوان بهصورت زیر نوشت:
$$\large \require{cancel}<br />
{\iint\limits_R {\sin \theta drd\theta } }<br />
= {\int\limits_0^{2\pi } {\int\limits_0^{1 + \cos \theta } {\sin \theta drd\theta } } } \\ \large<br />
= {\int\limits_0^{2\pi } {\left[ {\int\limits_0^{1 + \cos \theta } {dr} } \right]\sin \theta d\theta } }<br />
= {\int\limits_0^{2\pi } {\left[ {\left. r \right|_0^{1 + \cos \theta }} \right]\sin \theta d\theta } } \\ \large<br />
= {\int\limits_0^{2\pi } {\left( {1 + \cos\theta } \right)\sin \theta d\theta } }\<br />
= {\int\limits_0^{2\pi } {\left( {\sin \theta + \cos\theta \sin \theta } \right)d\theta } }\\ \large<br />
= {\int\limits_0^{2\pi } {\sin \theta d\theta } }+{ \int\limits_0^{2\pi } {\frac{{\sin 2\theta }}{2}d\theta } }<br />
= {\left. {\left( { – \cos \theta } \right)} \right|_0^{2\pi } }+{ \frac{1}{2}\left. {\left( { – \frac{{\cos 2\theta }}{2}} \right)} \right|_0^{2\pi } } \\ \large<br />
= {{ – \cos 2\pi + \cos 0 }-{ \frac{1}{4}\cos 4\pi }+{ \frac{1}{4}\cos 0 }}<br />
= { -\cancel{1} + \cancel{1} – \cancel{\frac{1}{4}} + \cancel{\frac{1}{4}} }={ 0.}$$
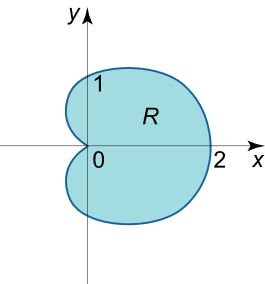
مثال ۴
انتگرال دوگانه ∬ R ( x 2 + y 2 ) d x d y \iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy} R ∬ ( x 2 + y 2 ) d x d y x 2 + y 2 = 2 x {x^2} + {y^2} = 2x x 2 + y 2 = 2 x
حل: ابتدا ناحیه R R R
x 2 + y 2 = 2 x , ⇒ x 2 – 2 x + 1 + y 2 = 1 , ⇒ ( x – 1 ) 2 + y 2 = 1. \large {{x^2} + {y^2} = 2x,\;\;}\Rightarrow {{x^2} – 2x + 1 + {y^2} = 1,\;\;}\Rightarrow {{\left( {x – 1} \right)^2} + {y^2} = 1.} x 2 + y 2 = 2 x , ⇒ x 2 –2 x + 1 + y 2 = 1 , ⇒ ( x –1 ) 2 + y 2 = 1.
با استفاده از تغییر متغیر x = r cos θ x = r\cos \theta x = r cos θ y = r sin θ y = r\sin \theta y = r sin θ
x 2 + y 2 = 2 x , ⇒ r 2 cos 2 θ + r 2 sin 2 θ = 2 r cos θ , ⇒ r 2 ( cos 2 θ + sin 2 θ ) = 2 r cos θ , ⇒ r = 2 cos θ . \large {{x^2} + {y^2} = 2x,\;\;}\Rightarrow {{{r^2}{\cos ^2}\theta + {r^2}{\sin^2}\theta }={ 2r\cos \theta ,\;\;}}\\ \large \Rightarrow {{{r^2}\left( {{{\cos }^2}\theta + {\sin^2}\theta } \right) }={ 2r\cos \theta ,\;\;}}\Rightarrow {r = 2\cos \theta .} x 2 + y 2 = 2 x , ⇒ r 2 cos 2 θ + r 2 sin 2 θ = 2 r cos θ , ⇒ r 2 ( cos 2 θ + sin 2 θ ) = 2 r cos θ , ⇒ r = 2 cos θ .
بعد از انتقال به مختصات قطبی، میتوانیم انتگرال را محاسبه کنیم:
∬ R ( x 2 + y 2 ) d x d y = ∬ S ( r 2 cos 2 θ + r 2 sin 2 θ ) r d r d θ = ∬ S r 3 d r d θ = ∫ – π 2 π 2 [ ∫ 0 2 cos θ r 3 d r ] d θ = 4 ∫ – π 2 π 2 [ ( r 4 4 ) ∣ 0 2 cos θ ] d θ = 4 ∫ – π 2 π 2 cos 4 θ d θ = 4 ∫ – π 2 π 2 ( 1 + cos 2 θ 2 ) 2 d θ = ∫ – π 2 π 2 ( 1 + 2 cos 2 θ + cos 2 2 θ ) d θ = ∫ – π 2 π 2 ( 3 2 + 2 cos 2 θ + 1 2 cos 4 θ ) d θ = ( 3 2 θ + sin 2 θ + 1 8 sin 4 θ ) ∣ – π 2 π 2 = ( 3 2 ⋅ π 2 + sin π + 1 8 sin 2 π ) − ( – 3 2 ⋅ π 2 – sin π – 1 8 sin 2 π ) = 3 π 2 . \large {\iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy} } = {\iint\limits_S {\left( {{r^2}{{\cos }^2}\theta + {r^2}{\sin^2}\theta } \right)rdrd\theta } }\\ \large = {\iint\limits_S {{r^3}drd\theta } } = {\int\limits_{ – \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left[ {\int\limits_0^{2\cos \theta } {{r^3}dr} } \right]d\theta } } = {4\int\limits_{ – \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left[ {\left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^{2\cos \theta }} \right]d\theta } } \\ \large = {4\int\limits_{ – \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {{{\cos }^4}\theta d\theta } } = {4\int\limits_{ – \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {{{\left( {\frac{{1 + \cos 2\theta }}{2}} \right)}^2}d\theta } } = {\int\limits_{ – \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left( {1 + 2\cos 2\theta + {{\cos }^2}2\theta } \right)d\theta } } \\ \large = {\int\limits_{ – \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left( {\frac{3}{2} + 2\cos 2\theta + \frac{1}{2}\cos 4\theta } \right)d\theta } } = {\left. {\left( {\frac{3}{2}\theta + \sin 2\theta + \frac{1}{8}\sin 4\theta } \right)} \right|_{ – \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} } \\ \large = {\left( {\frac{3}{2} \cdot \frac{\pi }{2} + \sin \pi + \frac{1}{8}\sin 2\pi } \right) }-{ \left( { – \frac{3}{2} \cdot \frac{\pi }{2} – \sin \pi – \frac{1}{8}\sin 2\pi } \right) } = {\frac{{3\pi }}{2}.} R ∬ ( x 2 + y 2 ) d x d y = S ∬ ( r 2 cos 2 θ + r 2 sin 2 θ ) r d r d θ = S ∬ r 3 d r d θ = – 2 π ∫ 2 π 0 ∫ 2 c o s θ r 3 d r d θ = 4 – 2 π ∫ 2 π ( 4 r 4 ) 0 2 c o s θ d θ = 4 – 2 π ∫ 2 π cos 4 θ d θ = 4 – 2 π ∫ 2 π ( 2 1 + cos 2 θ ) 2 d θ = – 2 π ∫ 2 π ( 1 + 2 cos 2 θ + cos 2 2 θ ) d θ = – 2 π ∫ 2 π ( 2 3 + 2 cos 2 θ + 2 1 cos 4 θ ) d θ = ( 2 3 θ + sin 2 θ + 8 1 sin 4 θ ) – 2 π 2 π = ( 2 3 ⋅ 2 π + sin π + 8 1 sin 2 π ) − ( – 2 3 ⋅ 2 π – sin π – 8 1 sin 2 π ) = 2 3 π .
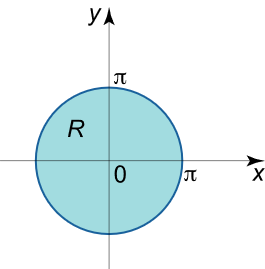
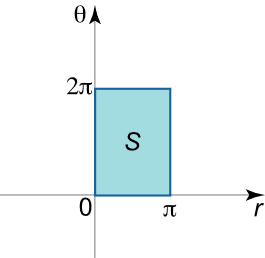
مثال ۵
انتگرال دوگانه ∬ R sin x 2 + y 2 d x d y \iint\limits_R {\sin \sqrt {{x^2} + {y^2}} dxdy} R ∬ sin x 2 + y 2 d x d y R R R x 2 + y 2 ≤ π 2 {x^2} + {y^2} \le {\pi ^2} x 2 + y 2 ≤ π 2
حل: ناحیه R R R
ناحیه S S S R R R
{ S = ( r , θ ) ∣ 0 ≤ r ≤ π , 0 ≤ θ ≤ 2 π } \large {\left\{ {S = \left( {r,\theta } \right)|\;0 \le r \le \pi ,\;}\right.}\kern0pt{\left.{ 0 \le \theta \le 2\pi } \right\} } { S = ( r , θ ) ∣ 0 ≤ r ≤ π , 0 ≤ θ ≤ 2 π }
انتگرال دوگانه در مختصات قطبی، بهصورت زیر نوشته میشود:
I = ∬ R sin x 2 + y 2 d x d y = ∬ S r sin r d r d θ = ∫ 0 2 π d θ ∫ 0 π r sin r d r = 2 π ∫ 0 π r sin r d r . \large {I }={ \iint\limits_R {\sin \sqrt {{x^2} + {y^2}} dxdy} } = {\iint\limits_S {r\sin rdrd\theta } } \\ \large = {\int\limits_0^{2\pi } {d\theta } \int\limits_0^\pi {r\sin rdr} } = {2\pi \int\limits_0^\pi {r\sin rdr} .} I = R ∬ sin x 2 + y 2 d x d y = S ∬ r sin r d r d θ = 0 ∫ 2 π d θ 0 ∫ π r sin r d r = 2 π 0 ∫ π r sin r d r .
انتگرال اخیر را میتوان با کمک انتگرالگیری جزء به جزء حل کرد:
∫ a b u d v = ( u v ) ∣ a b − ∫ a b v d u . \large {\int\limits_a^b {udv} } = {\left. {\left( {uv} \right)} \right|_a^b }-{ \int\limits_a^b {vdu} .} a ∫ b u d v = ( uv ) ∣ a b − a ∫ b v d u .
تساوی u = r u = r u = r d v = sin r d r dv = \sin rdr d v = sin r d r d u = d r du = dr d u = d r v = ∫ sin r d r v = \int {\sin rdr} v = ∫ sin r d r
I = 2 π ∫ 0 π r sin r d r = 2 π [ ( – r cos r ) ∣ 0 π − ∫ 0 π ( – cos r ) d r ] = 2 π [ ( – r cos r ) ∣ 0 π + ∫ 0 π cos r d r ] = 2 π [ ( – r cos r ) ∣ 0 π + ( sin r ) ∣ 0 π ] = 2 π ( sin r – r cos r ) ∣ 0 π = 2 π [ ( sin π – π cos π ) − ( sin 0 – 0 ⋅ cos 0 ) ] = 2 π ⋅ π = 2 π 2 . \large {I = 2\pi \int\limits_0^\pi {r\sin rdr} } = {{2\pi \Big[ {\left. {\left( { – r\cos r} \right)} \right|_0^\pi }}-{{ \int\limits_0^\pi {\left( { – \cos r} \right)dr} } \Big] }}\\ \large = {{2\pi \Big[ {\left. {\left( { – r\cos r} \right)} \right|_0^\pi }}+{{ \int\limits_0^\pi {\cos rdr} } \Big] }} = {2\pi \left[ {\left. {\left( { – r\cos r} \right)} \right|_0^\pi + \left. {\left( {\sin r} \right)} \right|_0^\pi } \right] } \\ \large = {2\pi \left. {\left( {\sin r – r\cos r} \right)} \right|_0^\pi } = {2\pi \left[ {\left( {\sin \pi – \pi \cos \pi } \right) }\right.}-{\left.{ \left( {\sin 0 – 0 \cdot \cos 0} \right)} \right] } = {2\pi \cdot \pi }={ 2{\pi ^2}.} I = 2 π 0 ∫ π r sin r d r = 2 π [ ( – r cos r ) ∣ 0 π − 0 ∫ π ( – cos r ) d r ] = 2 π [ ( – r cos r ) ∣ 0 π + 0 ∫ π cos r d r ] = 2 π [ ( – r cos r ) ∣ 0 π + ( sin r ) ∣ 0 π ] = 2 π ( sin r – r cos r ) ∣ 0 π = 2 π [ ( sin π – π cos π ) − ( sin 0–0 ⋅ cos 0 ) ] = 2 π ⋅ π = 2 π 2 .
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش انتگرال دوگانه در مختصات قطبی – به زبان ساده (+ دانلود فیلم آموزش گام به گام) فیلم آموزشی انتگرال دوگانه در مختصات قطبی فیلم آموزشی حل چند مثال از انتگرال دوگانه در مختصات قطبی 
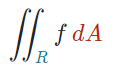
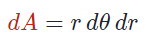
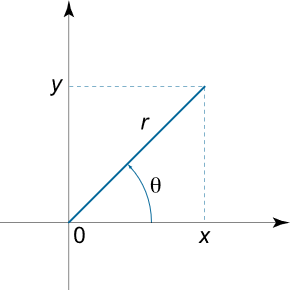













عالی :: خدا خیرتان بدهد
سلام نوید عزیز.
سپاس از همراهیتان با مجله فرادرس.
موفق باشید.