انتقال محور‌ها — به زبان ساده

در مطلب ماتریس دوران نحوه دوران یک شکل در دستگاه مختصات دکارتی را توضیح دادیم. از این رو در این مطلب قصد داریم تا فرآیندی را توضیح دهیم که در آن محور‌های مختصات به اندازه‌ای ثابت منتقل می‌شوند. توجه داشته باشید که با استفاده از انتقال محور‌ها می‌توان معادلات پیچیده مربوط به صفحات فضایی را ساده‌تر کرده و شکل آن‌ها را نیز تشخیص داد.

انتقال محور‌ها

در ریاضیات، انتقال محور‌ها در دو بعد، معادل با نگاشتی است که دستگاه مختصات $$ X Y $$ را به دستگاه مختصات $$ X ^ { \prime } Y ^ { \prime } $$ منتقل می‌کند. توجه داشته باشید که در این فرآیند بر خلاف دوران، راستای محور‌ها نسبت به یکدیگر ثابت می‌مانند.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

در اولین گام فرض کنید محور‌های یک دستگاه مختصات را با برداری همچون $$ ( h , k ) $$ جمع کنیم. در این صورت محور $$ Y $$ به اندازه $$ k $$ و محور $$ X $$ به اندازه $$ h $$ منتقل خواهند شد. در این شرایط تبدیل نقاط در دستگاه مختصات جدید با استفاده از دو رابطه زیر انجام می‌شود.

$$ {\displaystyle X = X ^ { \prime } + h } $$
$$ {\displaystyle Y = Y ^ { \prime } + k } $$

البته معادل با رابطه فوق را می‌توان به شکل زیر نیز بیان کرد:

$$ { \displaystyle X ^ { \prime } = X - h } \ \ , \ \ {\displaystyle Y ^ { \prime } = Y - k } $$

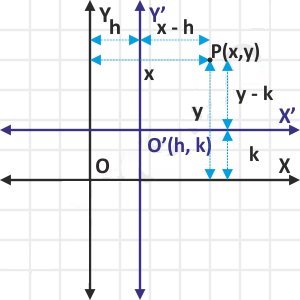
جالب است بدانید برای یک نقطه، انتقال به صورت عکس رخ می‌دهد. در حقیقت نقطه‌ای همچون $$ P $$ در دستگاه جدید به اندازه $$ ( - h , - k ) $$ جابجا می‌شود. برای نمونه اگر محور‌های مختصات به اندازه $$ h $$ به سمت راست و به اندازه $$ k $$ به سمت بالا منتقل شود، مختصات نقطه در دستگاه جدید به اندازه $$ h$$ به سمت چپ و $$ k $$ به سمت پایین منتقل خواهد شد. در شکل زیر، محور‌های منتقل شده و مختصات نقطه‌ای هم‌چون $$ P $$ در دو دستگاه مختلف نشان داده شده‌اند.

توجه داشته باشید که در حالت چندبعدی نیز می‌توان روابط فوق را به‌منظور انتقال بیان کرد. برای نمونه در حالت سه‌بعدی رابطه مربوط به انتقال برابر است با:

$$ \large {\displaystyle X ^ { \prime } = X - h \ \ , \ \ Y ^ { \prime } = Y - k \ \ , \ \ Z ^ { \prime } = Z - l } $$

رابطه فوق نشان می‌دهد که محور $$ Z $$ به اندازه $$ l $$، به سمت بیرون از صفحه جابجا شده است.

انتقال مقاطع مخروطی

با استفاده از انتقال مقاطع مخروطی می‌توان شکل استاندارد آن‌ها را تعیین کرد. در حقیقت در مواردی ممکن است با معادله‌ای روبرو شوید که شکل آن برای شما آشنا نباشد. پس از استفاده از تبدیلات مربوط به انتقال، شکل استاندارد آن بدست خواهد آمد. شکل کلی یک مقطع مخروطی به صورت زیر است.

$$ \large { \displaystyle A X ^ { 2 } + B X Y + C Y ^ { 2 } + D X + E Y + F = 0 } $$

فیلم آموزش هندسه پایه دهم – هندسه ۱ در فرادرس

کلیک کنید

در اکثر موارد می‌توان با استفاده از دوران، معادله یک مقطع مخروطی را به صورت زیر بیان کرد:

$$ \large { \displaystyle A X ^{ 2 } + C Y ^ { 2 } + D X + E Y + F = 0 } $$

همان‌طور که مشاهده می‌کنید با استفاده از دوران، ضریب $$ X Y $$ حذف می‌شود. در مرحله بعدی می‌توان با استفاده از انتقال، ضرایب $$ D $$ و $$ E $$ را نیز از بین برد. در ادامه مثال‌هایی ارائه شده که در آن‌ها فرآیند دوران از قبل انجام شده است. شکل زیر نمونه‌ای از انتقال را نشان می‌دهد. همان‌طور که می‌بینید در این فرآیند تمامی نقاط مثلث به یک صورت جابجا شده‌اند. به منظور تشخیص فرآیند انتقال به یاد داشته باشید که طول‌ تمامی خطوطی که نقاط مشابه را به هم وصل می‌کنند، باید مقداری برابر داشته باشند.

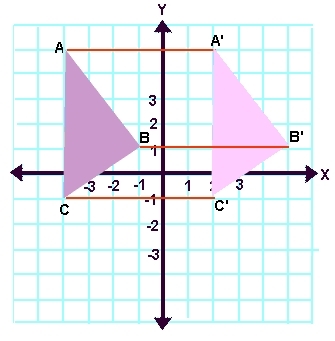
مثال ۱

معادله زیر را در نظر بگیرید.

$$ \large 9 X ^ 2 + 25 Y ^ 2 + 18 X - 100 Y - 116 = 0 $$

با استفاده از انتقال محور‌ها شکل معادله فوق را مشخص کنید.

در اولین گام عبارت‌های شامل $$ X $$ و $$ Y $$ را به صورت زیر جدا می‌کنیم.

$$ \large 9 ( X ^ 2 + 2 X ) + 25 ( Y ^ 2 - 4 Y ) = 116 $$

معادله فوق را می‌توان به صورت زیر نیز بازنویسی کرد.

$$ \large \begin {gather*} 9 ( X ^ 2 + 2 X + 1) + 25 ( Y ^ 2 - 4 Y + 4 ) = 116 + 9 + 100 \\ \\ {\displaystyle \Rightarrow 9 ( X + 1 ) ^ { 2 } + 2 5 ( Y - 2) ^ { 2 } = 225 } \end {gather*} $$

در گام بعد محور‌های $$ X ^ { \prime } $$ و $$ Y ^ { \prime } $$ را به صورت زیر تعریف می‌کنیم.

$$ \large X ^ { \prime } = X + 1 \ \ , \ \ { \displaystyle Y ^ { \prime } = Y - 2 } $$

تبدیلات فوق به معنای آن هستند که مقطع مخروطی ارائه شده در دستگاهی نوشته خواهد شد که به اندازه 1 به سمت چپ و به اندازه ۲ واحد به سمت بالا منتقل شده است. با قرار دادن تبدیل در نظر گرفته شده در معادله اصلی، شکل معادله به صورت زیر در خواهد آمد.

$$ \large {\displaystyle 9 X ^ {{ \prime } ^ { 2 }} + 25 Y ^ {{ \prime } ^ { 2 }} = 225 } $$

با تقسیم کردن معادله بالا به $$ 225 $$، داریم:

$$ \large \frac { X ^ {{ \prime } ^ { 2 }} } { 25 } + \frac { Y ^ {{ \prime } ^ { 2 }} } { 9 } = 1 $$

همان‌طور که می‌بینید معادله بدست آمده، نشان‌دهنده شکل یک بیضی با مشخصه‌های زیر است.

$$ \large { \displaystyle a = 5 , b = 3, c ^ { 2 } = a ^ {2 } -b ^ { 2} = 1 6 ,c = 4 , e = { \tfrac { 4 } { 5} } } $$

در رابطه فوق $$ a $$ و $$ b $$ نیم‌قطر‌های بزرگ و کوچک، $$ e $$ نشان‌دهنده خروج از مرکز بوده و $$ C $$ نیز کانون بیضی را نشان می‌دهد.

انتقال رویه‌های درجه دوم

در فضای سه‌بعدی، مرسوم‌ترین معادله به‌منظور نشان دادن شکل کلی رویه‌های درجه دوم به صورت زیر است.

$$ { \displaystyle A X ^ { 2 } + B Y^ { 2 } + C Z ^ { 2 } +D X Y + EX Z + F Y Z + G X + H Y + K Z + L = 0 } $$

فیلم آموزش ریاضی و آمار ۱ – پایه دهم علوم انسانی در فرادرس

کلیک کنید

توجه داشته باشید که ضرایب ثابت معادله فوق می‌توانند مثبت، منفی یا صفر باشند. هر معادله درجه دومی که توصیف کننده استوانه‌، خط، صفحه، نقطه یا دایره نباشد، رویه‌ای درجه دوم تلقی می‌شود. هم‌چنین ممکن است یک معادله درجه دوم با استفاده از انتقال محور‌ها ساده‌تر شده و نهایتا شکل معادله به‌صورت نوعی خاص از رویه‌های درجه دوم درآید. پرکاربردترین روش به‌منظور ساده‌سازی، روش مربع کامل است.

مثال ۲

معادله ارائه شده در ادامه چه نوع رویه‌ای را توصیف می‌کند.

$$ \large X ^ 2 + 4 Y ^ 2 + 3 Z ^ 2 + 2 X - 8 Y + 9 Z = 10 $$

در ابتدا معادله فوق را به‌صورت زیر بازنویسی کرده و در فضای خالی باید اعدادی قرار گیرند که مجموع عبارت را به صورت مربع کامل درآورند.

$$ \large X ^ 2 + 2 X \qquad + 4 ( Y ^ 2 - 2 Y \qquad ) + 3 ( Z ^ 2 + 3 Z \qquad ) = 10 $$

در نتیجه معادله مربع کامل را می‌توان به صورت زیر بازنویسی کرد:

$$ \large { ( X + 1 ) ^ 2 + 4 ( Y - 1 ) ^ 2 + 3 ( Z + \tfrac { 3 } { 2 } ) ^ 2 = 10 + 1 + 4 + \tfrac { 27} { 4 } } $$

بنابراین محور‌های اولیه را مطابق با روابط زیر منتقل می‌کنیم.

$$ \large {\displaystyle X ^ { \prime } = X + 1 , \qquad Y ^ { \prime }= Y - 1 , \qquad Z ^ { \prime }= Z + { \tfrac { 3 } { 2 } } } $$

نهایتا شکل معادله در دستگاه جدید برابر است با:

$$ \large X ^{\prime 2} + 4 Y ^{\prime 2} + 3 Z ^{\prime 2} = \large \tfrac { 8 7} { 4 } $$

معادله فوق نشان‌دهنده کره‌ای به شعاع $$ \frac { \sqrt { 87 } } { 2 } $$ است. بنابراین دیدید که با استفاده از انتقال محور‌ها، معادله اصلی ساده‌تر شده و با ساده‌تر شدن آن شکل اصلی معادله مشخص شد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• مجموعه آموزش‌های ریاضی و فیزیک
• رویه‌های درجه دوم — به زبان ساده
• ماتریس دوران — به زبان ساده
• تعریف مقطع مخروطی و مفاهیم مرتبط با آن - به زبان ساده

^^