اصل طرد پائولی چیست؟ – از صفر تا صد
اصل طرد پائولی یکی از مهمترین اصلها در کنار اصل آفبا و قانون هوند در علوم شیمی و فیزیک است. یادگیری و آشنایی با مفهوم این اصل برای دانشجویان و دانشآموزانی که در مورد الکترونها مطالعه میکنند بسیار ضروری خواهد بود. اصل طرد پائولی به ما در فهم آرایش الکترونی عناصر و همچنین طبقهبندی و چینش عناصر در جدول تناوبی کمک میکند. همچنین طبق این اصل هیچ دو الکترونی در جهان نمیتوانند حالت کوانتومی یکسانی را اشغال کنند. در این مبحث به مطالعه اصل طرد پائولی میپردازیم و با مفاهیم این اصل آشنا میشویم.

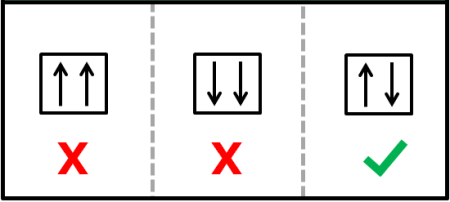
اصل طرد پائولی چیست ؟
بر طبق «اصل طرد پائولی» (Pauli exclusion principle)، هیچ دو الکترونی در اتم، اعداد کوانتومی (s، m، l، و n) یکسانی نخواهند داشت. به زبان ساده هر الکترون باید در حالت یکتای خود باشد (حالت یگانه). این اصل از دو قانون پیروی میکند:
- تنها دو الکترون میتوانند اوربیتال یکسانی را اشغال کنند.
- دو الکترونی که در اوربیتال یکسانی قرار دارند دارای اسپینهای مخالف هستند یا به بیان سادهتر موازی یکدیگر نیستند.
ولی چرا به این اصل، اصل طرد گفته میشود؟ زیرا مطابق با این اصل اگر الکترونی در اتم دارای مقادیر یکسانی برای اعداد کوانتومی باشد، الکترونهای دیگر در آن اتم از داشتن اعداد کوانتومی با مقادیر مشابه محروم خواهند شد. قبل از آشنایی با اصل طرد پائولی ابتدا به تاریخچه پیدایش این اصل پرداخته میشود.
برای درک اصل طرد پائولی نیاز است در ابتدا با چهار عدد کوانتومی آشنا شویم.
عدد کوانتومی چیست؟
برای توصیف حرکت هر الکترون در اتم از چهار عدد کوانتومی استفاده میشود. ترکیب اعداد کوانتومی همه الکترونها در اتم با استفاده از تابع موج توصیف میشود. تابع موج از حل معادله شرودینگر به دست میآید. یکی از کاربردهای اصلی اعداد کوانتومی تعیین آرایش الکترونی اتمها و مکان احتمالی قرارگیری الکترونها است. همچنین، از اعداد کوانتومی برای فهمیدن ویژگیهای اتم مانند انرژی یونش و شعاع اتمی استفاده میشود.
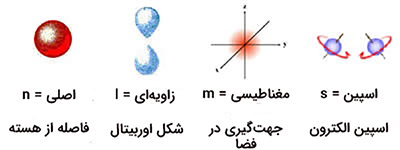
در اتمها، چهار عدد کوانتومی وجود دارند.
- عدد کوانتومی اصلی (n)
- عدد کوانتومی فرعی چرخشی (l) یا عدد کوانتومی فرعی
- عدد کوانتومی مغناطیسی ()
- عدد کوانتومی اسپین الکترون ()
عدد کوانتومی اصلی، n، توصیف کننده انرژی الکترون و محتملترین فاصله الکترون از هسته است. به بیان دیگر، این عدد اندازه اوربیتال و تراز انرژی را نشان میدهد که الکترون در آن قرار دارد. عدد زیرلایهها یا l شکل اوربیتالها را تعیین میکند. عدد کوانتومی مغناطیسی یا تعیین کننده ترازهای انرژی در زیر لایه است. نیز مربوط به اسپین الکترون است که در دو حالت بالا یا پایین قرار دارد.
عدد کوانتومی اصلی (n)
همانطور که در بالا اشاره شد عدد کوانتومی اصلی، n، لایه اصلی الکترون را معین میکند. از آنجایی که n تعیین کننده محتملترین فاصله الکترونها از هسته اتم است، هر چه مقدار آن بزرگتر باشد الکترون در فاصله دورتری از هسته قرار دارد. در نتیجه، اندازه اوربیتال و همچنین اندازه اتم بزرگتر خواهد بود. مقدار n میتواند هر عدد صحیح مثبتی باشد. حالت n=1 نشاندهنده اولین لایه اصلی یا داخلیترین لایه است که به آن پایینترین حالت انرژی یا حالت زمینه (پایه) گفته میشود. چون از نظر فیزیکی وجود ترازهای انرژی صفر یا منفی امکانپذیر نیست مقدار n نمیتواند منفی یا صفر باشد. هنگامی که الکترون انرژی به دست میآورد یا در حالت برانگیخته است به لایه اصلی دوم یعنی n=2 پرش میکند (جذب). الکترونها به هنگام پرش به لایههای اصلی پایینتر (n کمتر) انرژی ساطع میکنند(نشر).
سوال: به هنگام پرش الکترون از تراز انرژی n=5 به تراز انرژی n=3 کدام پدیده جذب یا نشر اتفاق میافتد.
پاسخ: نشر، زیرا با تابش فوتون انرژی از بین رفته است.
عدد کوانتومی فرعی (l)
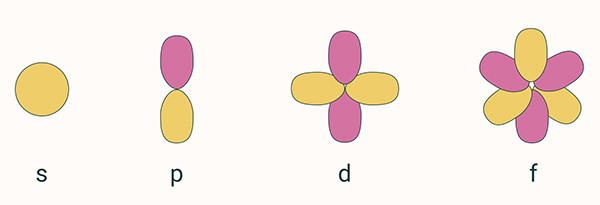
این عدد کوانتومی توصیف کننده شکل اوربیتال است و به ما میگوید کدام زیرلایه در لایه اصلی قرار دارد. در واقع این عدد، لایهها را به زیرلایهها تقسیم میکند. کمترین مقداری که «l» میتواند داشته باشد برابر صفر است. جدول زیر به ما نشان میدهد که هر زیرلایه معادل کدام مقدار «l» خواهد بود.
| عدد کوانتومی فرعی (l) | نام زیرلایه |
| 0 | s |
| ۱ | p |
| ۲ | d |
| ۳ | f |
مقدار l همچنین تعداد گرههای موجود در اوربیتال را نشان میدهد. گره، ناحیهای در اوربیتال است که در آنجا احتمال یافتن الکترونها صفر خواهد بود. به طور مثال اگر مقدار l برابر ۳ باشد، در این زیر لایه سه گره وجود دارد. اینکه l چه مقداری داشته باشد به اندازه عدد کوانتومی اصلی به صورت زیر بستگی دارد.
در تصویر زیر شکل اوربیتالهای s، p، d و f مشاهده میشود.
عدد کوانتومی مغناطیسی () چیست؟
عدد کوانتومی مغناطیسی تعیین کننده تعداد اوربیتالها و جهتگیری آنها در زیرلایه است. در نتیجه مقدار آن به l بستگی دارد. با داشتن مقدار l، مقدار () از l- تا l+ تغییر میکند.
به طور مثال اگر مقدار l برابر ۲ باشد مقادیر برابر ۲-، 1-، 0، 1 و ۲ خواهد بود.
در ادامه حالتهای مختلف l از یک تا چهار توضیح داده شده است.
- اگر l=0 باشد، طبق جدول در زیرلایه s قرار داریم. در نتیجه مقدار برابر صفر خواهد بود. از آنجایی که یک مقدار دارد، زیرلایه s تنها دارای یک اوربیتال به نام اوربیتال s خواهد بود.
- اگر ۱=l باشد، در زیر لایه p قرار داریم. مقدار برابر 1-، 0 و 1 خواهد بود. از آنجایی که دارای سه مقدار است، زیر لایه p از سه اوربیتال ، و تشکیل شده است که به ترتیب در راستای محورهای قرار دارند.
- اگر ۲=l باشد، در زیر لایه d قرار داریم. مقدار برابر 2-، 1-، 0، 1 و 2 خواهد بود. در نتیجه زیر لایه d دارای پنج اوربیتال ، ، ، و است. همانطور که در تصویر زیر مشاهده میشود اوربیتال به طور کامل در صفحه xy قرار گرفته است. به طور مشابه اوربیتالهای و نیز به طور کامل در صفحههای xz و yz قرار گرفتهاند. اوربیتال نیز همانگونه که در تصویر نشان داده شده است از دو دمبل در راستای محورهای x و y تشکیل شده است. پنجمین اوربیتال یعنی تنها در راستای محور z قرار گرفته است.
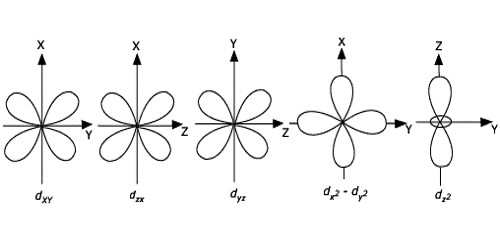
- اگر 3=l باشد، در زیر لایه f قرار داریم. از آنجایی که مقادیر برابر 3-، 2-، 1-، 0، 1، 2 و ۳ خواهند بود، زیر لایه f از هفت اوربیتال تشکیل میشود.
عدد کوانتومی اسپین الکترون ()
قبل از توضیح در مورد این عدد کوانتومی ابتدا در مورد اسپین توضیح میدهیم.
اسپین نوعی تکانه زاویه ای است. برخی ذرات دارای تکانه زاویه ذاتی هستند. در واقع این ذرات به جای چرخش به دور جسم دیگر، به دور خود میچرخند. ولی سوالی که مطرح میشود آن است که منشا این تکانه زاویه ذاتی چیست؟ پاسخ به این پرسش در اثر نسبیت خاص در مکانیک کوانتوم نهفته است. اسپین الکترون دارای دو حالت اسپین بالا و اسپین پایین است. در واقع دارا بودن دو حالت برای اسپین الکترون بدان معنا است که الکترون به صورت پادساعتگرد (اسپین بالا) یا ساعتگرد (اسپین پایین) به دور خود میچرخد.
برخلاف اعداد کوانتومی n، l و ، عدد کوانتومی اسپین الکترون، به دیگر اعداد کوانتومی وابسته نیست. همانطور که گفته شد اسپین الکترون دارای دو حالت بالا و پایین است. مقدار تعیین کننده جهت اسپین الکترون است.
| اسپین بالا | ||
| اسپین پایین |
پس از آشنایی با اعداد کوانتومی در ادامه به توضیح اصل طرد پائولی و چگونگی پر شدن اتمها به زبان ساده میپردازیم.
اصل طرد پائولی به زبان ساده
به منظور درک چگونگی آرایش الکترونها در اتم، سیستمی دو الکترونی را در نظر میگیریم. الکترونها مهمترین مثال از گروه فرمیونها هستند.
از اینرو در سیستم دو الکترونی نمیتوانیم برای الکترونها شماره ۱ و ۲ یا برچسب بگذاریم. به بیان دیگر، الکترونها ذرات غیرقابل تشخیص از یکدیگر هستند. برای سیستم دو الکترونی ابتدا حالت نمایش داده شده در تصویر زیر را در نظر میگیریم. در این حالت تابع احتمال قرار گرفتن سیستم به صورت بیان میشود.
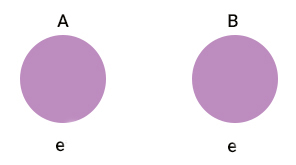
حال اگر آرایش سیستم دو الکترونی به صورت زیر تغییر کند، تابع احتمال سیستم به صورت نوشته میشود.

به زبان ریاضی وقتی میگوییم الکترونها ذرات غیرقابل تشخیص هستند یعنی تابع احتمال سیستم در حالت AB برابر تابع احتمال آن در حالت BA است.
با گرفتن جذر از معادله بالا داریم.
طبق رابطه بالا، به هنگام تعویض دو ذره، برای تابع موج دو حالت اتفاق میافتد.
- تابع موج تغییر نمیکند (علامت مثبت در رابطه بالا). این حالت برای نوعی از ذرات به نام بوزونها اتفاق میافتد.
- تابع موج قرینه میشود (علامت منفی در رابطه بالا). این حالت برای فرمیونها رخ میدهد.
به دلیل آنکه الکترونها جزو دسته فرمیونها طبقهبندی شدهاند در نتیجه در سیستم دو الکترونی بالا، هنگام تعویض دو الکترون، تابع موج سیستم قرینه میشود. به تابع موج سیستم در این حالت تابع موج پادمتقارن میگوییم. این تابع موج برای سیستم دو الکترونی به صورت زیر نوشته میشود.
اکنون دو حالت انرژی ۱ و۲ برای سیستم دو الکترونی مفروض در نظر بگیرید. در نتیجه تابع موج نوشته شده برای این سیستم به صورت شماتیک، نمایش دهنده دو حالت زیر است.
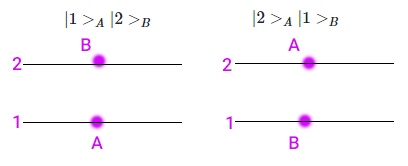
تابع موج نوشته شده، برهمنهی دو حالت نشان داده شده در تصویر است. اکنون اگر انرژی این سیستم دو الکترونی را اندازه بگیریم، یکی از دو حالت نشان داده شده در تصویر بالا به دست خواهد آمد. حالتی که در آن دو الکترون در یک تراز انرژی قرار داشته باشند به دست نمیآید. اکنون به اصل طرد پائولی رسیدیم. طبق این اصل، هیج دو فرمیونی (در اینجا الکترون) حالت کوانتومی یکسانی را اشغال نمیکنند. حالت کوانتومی توسط چهار عدد کوانتومی بالا توضیح داده میشود. بر طبق اصل طرد پائولی، هیچ دو الکترونی در جهان چهار عدد کوانتومی یکسان ندارند. در واقع، برای دو الکترون حداقل یکی از این چهار اعداد باید با یکدیگر متفاوت باشند. اکنون میتوانیم به سوالات زیر پاسخ دهیم.
سوال ۱. چرا پایینترین تراز انرژی (n=1) توسط دو الکترون اشغال میشود؟
پاسخ. برای این حالت مقادیر l و برابر صفر هستند. در نتیجه برای دو الکترون سه عدد کوانتومی n، l و با یکدیگر برابر هستند و تنها میتواند متفاوت باشد. از اینرو، تراز انرژی اول میتواند تنها توسط دو الکترون با اسپینهای مخالف اشغال شود.
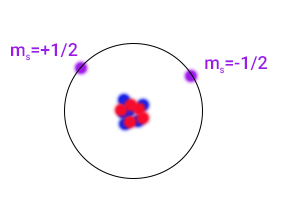
سوال 2. چرا دومین تراز انرژی (n=2) توسط هشت الکترون اشغال میشود.
پاسخ. برای حالت n=2 داریم.
در نتیجه تعداد بیشتری الکترون میتوانند در تراز انرژی دوم (هشت الکترون) قرار بگیرند.
در هر زیرلایه چند الکترون جای می گیرد ؟
نکته ۱: هر زیرلایه دارای حداکثر الکترون است.
در هر لایه چند الکترون جای می گیرد ؟
نکته2: هر لایه دارای حداکثر الکترون است.
در ادامه به حل چند مثال کاربردی میپردازیم.
حل چند مثال کاربردی
در ادامه به منظور درک بهتر اعداد کوانتومی اصلی به حل چند مثال میپردازیم.
مثال ۱
برای n=3 تعداد زیرلاها را به دست آورید. با مشخص کردن هر زیرلایه، حداکثر تعداد الکترونی که در آن زیرلایه قرار میگیرد را حساب کنید. در ادامه ثابت کنید که تعداد کل الکترونها برای n=3 از نکته ۲ پیروی میکند.
پاسخ.
تعداد زیرلایهها با مقدار l تعیین میشود. در نتیجه در ابتدا مقادیر l را به دست میآوریم و در ادامه با استفاده از نکته ۱، حداکثر تعداد الکترونی را که در هر زیرلایه قرار میگیرد به دست میآوریم.
برای n=3 مقادیر l برابر است با
در نتیجه برای n=3 سه زیرلایه به صورت ۳s، ۳p و ۳d وجود دارد. با استفاده از نکته ۱ داریم.
بنابراین تعداد کل الکترونها برابر ۱۸ خواهد بود. از سوی دیگر، طبق نکته ۲ هر لایه دارای حداکثر الکترون است. اگر به جای n مقدار ۳ را قرار دهیم، حداکثر تعداد الکترونها ۱۸ به دست میآید که با مقدار به دست آمده از جمع الکترونهای هر زیرلایه برابر است.
مثال ۲
اتم Ne دارای ده الکترون است. برای این اتم ساختار الکترونی را به دست آورید.
پاسخ. اولین تراز انرژی 1s است که طبق اصل طرد پائولی با دو الکترون با دو جهت مخالف پر میشود. دومین تراز انرژی دارای دو زیرلایه 2s و 2p است. زیرلایه s یک اوربیتال و زیرلایه p سه اوربیتال دارد. حالت ۲s با دو الکترون در جهتهای مخالف پر میشود. برای پر کردن زیر لایه p که دارای سه اوربیتال با انرژی یکسان است از قانون هوند استفاده میکنیم. طبق قانون هوند داریم.
- اوربیتالهای همانرژی در زیرلایه ابتدا توسط یک الکترون پر میشوند و سپس اضافه شدن الکترونهای بعدی به صورت جفت ادامه مییابد.
- همه الکترونها در اوربیتالهای اشغال شده به صورت تکی به منظور ماکزیمم شدن اسپین کل، اسپین یکسانی دارند.
در نتیجه طبق قانون هوند، ابتدا سه اوربیتال p با سه الکترون با اسپینهای (اسپین رو به بالا) پر میشوند. سپس الکترونهای باقیمانده با اسپینهای با جهت مخالف در اوربیتالها قرار میگیرند.
مثال ۳
برای ، چهار عدد کوانتومی اصلی را تعیین کنید.
پاسخ. عدد ۳ در کنار p نشان دهنده n است. در نتیجه
n=3
برای زیرلایه p عدد l برابر با 1 است. زیرلایه p دارای سه اوربیتال است. همچین برای به دست آوردن مقدار عدد کوانتومی به اوربیتالی توجه میکنیم که آخرین الکترون، آن را اشغال میکند.

همانطور که در تصویر بالا مشاهده میکنید آخرین الکترون در اوربیتالی با قرار گرفته است. در نتیجه مقدار برابر صفر است. همچنین مقدار برابر است زیرا جهت پنجمین الکترون به سمت پایین است.
مثال 4
برای ، چهار عدد کوانتومی اصلی را تعیین کنید.
پاسخ. مقدار n برابر ۴ است. همچنین هنگامی که زیرلایه d باشد مقدار l=2 خواهد بود. زیرلایه d پنج اوربیتال دارد که چهار الکترون به صورت زیر در آنها جای داده میشود.
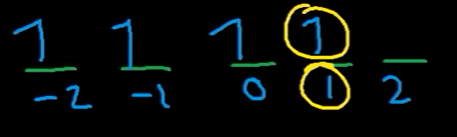
از آنجایی که چهارمین الکترون در اوربیتال با قرار گرفته است مقدار نیز مشخص میشود. همچنین با توجه به آنکه جهتگیری الکترون به سمت بالا است، مقدار برابر خواهد بود.
مثال 5
برای ، چهار عدد کوانتومی اصلی را تعیین کنید.
پاسخ. مقادیر n و l به صورت زیر به دست میآیند.
زیرلایه f دارای هفت اوربیتال است. طبق قانون شماره ۱ هوند ابتدا اوربیتالهای همانرژی توسط یک الکترون با اسپین رو به بالا پر میشوند. در اینجا ۱۳ الکترون داریم که در ابتدا یک الکترون با اسپین رو به بالا در هر اوربیتال قرار میگیرد. پس از پر شدن اوربیتالها با یک الکترون، شش الکترون باقیمانده با اسپین مخالف (روبه پایین) به صورت زیر در اوربیتالها جا داده میشوند.
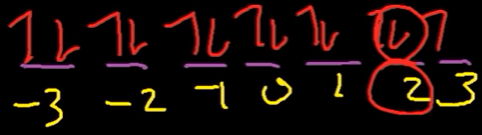
با توجه به شکل بالا مقدار و به ترتیب برابر 2+ و به دست میآیند.
با حل مثالهای بالا با روش به دست آوردن چهار عدد کوانتومی برای الکترون آشنا شدیم. همچنین طبق اصل طرد پائولی میدانیم چهار عدد کوانتومی برای هیچ دو الکترونی یکسان نیست. در نتیجه با داشتن مقادیر اعداد کوانتومی میتوانیم الکترون مورد نظر را تعیین کنیم.
مثال تعیین اوربیتال الکترون
با داشتن اعداد کوانتومی زیر، الکترون در کدام اوربیتال را اشغال کرده است.
پاسخ. به دلیل آنکه n=3 و l=2 است، الکترون مورد نظر در سومین لایه اصلی و در زیرلایه d قرار گرفته است. زیرلایه d پنج اوربیتال دارد.

با توجه به حل مثالهای قبل، مقادیر و الکترون مورد نظر است.
پس از آشنایی با مفهوم اعداد کوانتومی و اصل طرد پائولی به زبان ساده، برای درک عمیقتر این مفاهیم و چگونگی حل معادله شرودینگر میتوانید به فیلم آموزش مروری بر مکانیک کوانتومی مراجعه کنید.
معرفی فیلم آموزش مروری مکانیک کوانتومی ۲
مجموعه فرادرس در تهیه و تولید محتوای آموزشی خود اقدام به تهیه فیلم آموزش مروری مکانیک کوانتومی ۲ برای دانشجویان رشته فیزیک کرده است. این مجموعه آموزشی از هشت درس تشکیل شده است.
درسهای یکم تا سوم به حل معادله شرودینگر در سه بعد و حل این معادله برای اتم هیدروژن اختصاص دارد. در درسهای چهارم، پنجم و ششم با مفاهیم اعداد کوانتومی و آرایش الکترونی آشنا خواهید شد.
- برای دیدن فیلم آموزش مروری مکانیک کوانتومی ۲ + اینجا کلیک کنید.
تاریخچه پیدایش اصل طرد پائولی
پس از آشنایی با اصل طرد پائولی، در ادامه تاریخچه پیدایش این اصل بیان میشود.
بین سالهای 1920 تا 1930 تحولات زیادی در علم فیزیک اتمی رخ داد. دانشمندان زیادی طی سالهای متمادی تلاش کردند تا طبیعت ماده را توضیح دهند. این تلاشها با ارائه مدل اتمی بور در سال 1913 در مسیر جدیدی قرار گرفت. با این حال این مدل در توضیح بسیاری از رفتارهای مواد ناکام ماند.
مدل اتمی بور پیشنهاد داد که الکترونها تنها در مکانهای مشخصی به نام لایه و در خارج از هسته اتم قرار دارند. الکترونهایی که در لایههای ۱، ۲، ۳ و ... قرار میگیرند به ترتیب با اعداد کوانتومی ۱، 2، ۳ و ... نشان داده میشوند.
دانشمندان در آن سالها دریافتند که به منظور توصیف کامل رفتار الکترونها در مدار خود اعداد کوانتومی بیشتری مورد نیاز است. به طور مثال، «آرنولد سامرفیلد» (Arnold Sommerfeld) در سال 1915 به این نتیجه رسید که مدار چرخش الکترونها به دور هسته بیضی است. سامرفیلد برای این مدار بیضوی دومین عدد کوانتومی را معرفی کرد. تا اواسط سال 1920، دو عدد کوانتومی دیگر نیز به نامهای عدد کوانتوم مغناطیسی و عدد کوانتوم اسپین معرفی شدند.

کاربردهای اصل طرد پائولی
پس از آشنایی با اصل طرد پائولی به مهمترین کاربردهای این اصل پرداخته میشود.
- با کمک این اصل میتوان بسیاری از پدیدههای فیزیکی را مانند ساختار الکترونی اتمها و نحوه به اشتراکگذاری الکترونها توسط اتمها را توضیح داد.
- با کمک این اصل شکلگیری پیوندهای شیمیایی توضیح داده میشود.
- توضیح نحوه قرار گرفتن عناصر در جدول تناوبی
- بسیاری از ویژگیهای الکتریکی، اپتیکی، مکانیکی، مغناطیسی و شیمیایی جامدات در نتیجه اثر اصل طرد پائولی است.
- با کمک این اصل میتوان پایداری سیستمهای بسذرهای را توضیح داد.
- علاوه بر شیمی، این اصل یکی از بخشهای اصلی مکانیک کوانتوم در فیزیک است.
- این اصل در فیزیک نجوم نیز مورد استفاده قرار میگیرد.
نکات کلیدی اصل طرد پائولی
این مبحث را با ذکر مهمترین نکات بیان شده به پایان میرسانیم.













در جهان؟یا در اتم ؟
فرقی نداره
هیچ دو اتمی دقیقا شبیه هم نیستند
بالاخره در فضا زمان جایگاه ویژه ای دارن