ارزش زمانی پول چیست؟ – مفاهیم اولیه و نحوه محاسبه | به زبان ساده
یکی از مهمترین ابزارها در مدیریت منابع مالی و سرمایه گذاری، ارزش زمانی پول است. ما عموماً به این فکر میکنیم که جریان نقدینگی آتی در حال حاضر چه ارزشی دارد تا بتوانیم مدیریت مالی شخصی مناسبی داشته باشیم. برای درک بهتر مفهوم ارزش زمانی پول، به این مورد توجه کنید که ارزش ۱۰ هزارتومان در سال ۱۴۰۰ برابر با ارزش همین مبلغ در سال ۱۳۸۰ نیست. در نوشتار پیشرو، به اصلیترین موارد پیرامون محاسبه ارزش زمانی پول پرداختهایم.


اگر امکان انتخاب دریافت ۱۰۰ میلیون تومان پول را امروز یا یکسال دیگر داشته باشید، احتمالاً ترجیح میدهید که آنرا امروز دریافت کنید. دلایل زیادی برای این انتخاب وجود دارد.
- میتوانید این پول را برای تامین نیازهای اولیه برای مثال غذا و مسکن استفاده کنید و اگر قبلاً این نیازها تامین شده بودند، این مبلغ را برای رفع سایر احتیاجات خود مانند حملونقل، پوشاک یا کتابها بکار بگیرید.
- میتوانیم پولی که امروز دریافت کردهایم را سرمایهگذاری کنیم و آنرا افزایش دهیم. بازدهی سرمایهگذاری در بازار بورس در سالهای اخیر، قابل توجه بوده است. اگر ریسک پذیری سرمایهگذاری پول در بازار سهام را نداریم، میتوانیم گزینههایی مطمئنتری را انتخاب کنیم.
- نباید از نقش تورم غافل شویم. نرخ تورم در ایران در اغلب سالهای پیش، دورقمی بوده است. با وجود تورم، ممکن است دستگاه اتومبیلی را که امسال با قیمت ۲۰۰ میلیون تومان فروختهاید، نتوانید در سال آینده با ۳۰۰ میلیون تومان هم تهیه کنید. در نتیجه، نمیتوان با ۱۰۰ میلیون تومانی که سال آینده دریافت میکنید، کالاها و خدماتی را که حال با ۱۰۰ میلیون تومان عرضه میشود، تهیه کرد. در واقع، با وجود تورم مثبت، با گذشت زمان، قدرت خرید پول، کاهش مییابد.
- در دیدگاه روانشناسی، انسانها تمایل دارند موارد مطلوب و رضایتبخش را سریعتر دریافت کنند و دریافت مواردناپسند و نامطلوب را به تاخیر بیندازند. اگر ۱۰۰ میلیون تومان را امروز دریافت کنید، میتوانید سریعتر نسبت به تهیه کالاها و خدمات موردنیاز خود اقدام کنید. با دریافت این مبلغ پول در سال دیگر، باید تا یکسال از خرید تمام کالاهای دلخواه خود محروم شوید.
- عدم اطمینان به دریافت پول پس از یکسال انتظار، باعث میشود که افراد ریسکگریز تمایل داشته باشند که هرچه زودتر، پول را دریافت کنند.
ارزش زمانی پول چیست ؟
«ارزش زمانی پول» (Time Value of Money | TVM) یکی از اصلیترین مفاهیم در مدیریت مالی یا «فایننس» (Finance) به شمار میرود.
این مفهوم بیان میکند که پولی که امروز به آن دسترسی داریم ارزشی بیشتر از پول بدست آمده در آینده دارد. برای بدست آوردن ارزش فعلی پول کسب شده در آینده از تنزیل و برای بدست آوردن ارزش آتیِ پول در دسترس امروز، از نرخ بهره استفاده میکنیم.

تعریف ارزش فعلی چیست؟
در فایننس، به ارزش پول در زمانهای مختلف، اسامی متنوعی اختصاص داده شده است. در محاسبات مالی، پول دریافت شده امروز را «ارزش فعلی» ( Present Value | PV) مینامند. ارزش فعلی، نشاندهنده ارزش مبلغ پول شما در حال حاضر است.
تعریف ارزش آتی چیست؟
«ارزش آتی» (Future Value | FV) نشاندهنده ارزش پول در دست شما در آینده است. با دو روش میتوان به محاسبه ارزش پول فعلی در آینده پرداخت. بسته به ساده یا مرکب بودن نرخ بهره تعلق گرفته به منابع مالی، ارزش آنها در آینده با ارزش فعلی آنها تفاوت خواهد داشت. به صورت کلی، تبدیل ارزش فعلی به ارزش آتی را «مرکب کردن» (Compounding) و تبدیل ارزش آتی به ارزش فعلی را «تنزیل» (Discounting) مینامند.
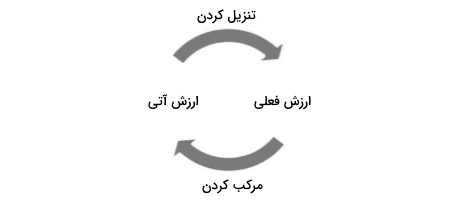
ارزش زمانی پول در آینده از جمع ارزش فعلی پول با نرخ بهره بدست میآید.
بهره + ارزش فعلی = ارزش آتی
اغلب تراکنشهای مالی شامل نرخ بهره مرکب، با این حال، بعضی از تراکنشهای مصرفکنندگان دارای «بهره ساده» (Simple Interest) هستند. با وجود نرخ بهره ساده، مبلغ بازپرداختی معادل اصل سرمایه به همراه بهره تعلق گرفته است. یعنی بهره تنها بر سرمایه اصلی یا مبلغ استقراضی وضع میشود. برای مثال، اگر شما ۱ میلیون تومان را با وجود بهره ۵ درصد قرض بگیرید و وام را پس از دوسال بازپرداخت کنید، باید ۱ میلیون تومان را به همراه دوسال بهره تعلق گرفته بپردازید.
۱ میلیون و ۱۰۰ هزار تومان = (۱ میلیون تومان × 2 × 0٫۰۵) + ۱ میلیون تومان = بازپرداخت با بهره ساده
در نرخ بهره مرکب، مبلغ پرداختی شامل ۳ جزء مبلغ استقراضی، بهره تعلق گرفته به مبلغ استقراضی و بهره وضع شده بر بهره است.
نرخ بهره چیست؟
«نرخ بهره» (Interest) برگرفته از واژه لاتین (Intereso) به معنی «گم شدن» است. مفهوم این کلمه به صورت کلی به این اشاره دارد که با قرض دادن پول و کالاها، فرد قرضدهنده دچار ضرر میشود زیرا خود دیگر نمیتواند از آنها استفاده کند.
نرخ بهره، درواقع، هزینه فرصت مبالغ مالی و عدم اطمینان نسبت به بازپرداخت مبلغ استقراضی و به صورت همزمان نشاندهنده هزینه زمان و هزینه ریسک است. قیمت زمان، همان هزینه فرصت مبالغ است، اینکه با این مبلغ میتوانستید چه کارهای دیگری را انجام بدهید. قیمت ریسک شامل ضررهای محتمل ناشی از قرض دادن پول به افراد است.
چگونه ارزش آتی پول را محاسبه کنیم؟
معادله زیر یکی از اصلیترین معادلات در مبحث ارزش زمانی پول است. اگر مبلغی پول با ارزش فعلی را در بانکی نگهداری کنیم که نرخ بهره (نرخ بهره را ممکن است با یا نشان دهند) را پرداخت میکند، پس از یکسال این مبلغ معادل خواهد بود. همانطور که بالاتر گفته شد، ارزش آتی پول را با نمایش میدهیم. پس ارزش آتی پول به شکل زیر از ضرب ارزش فعلی در نرخ بهره محاسبه میشود.
ممکن است را عامل رشد، در نظر بگیرید که البته همان ضریب مرکب شدن است. با ادامه دادن این فرایند برای یکسال بعد و مرکب شدن نرخ بهره، ارزش زمانی پول در آینده به صورت زیر محاسبه خواهد شد.
فرمول بالا، ارزش زمانی پول را پس از دو سال محاسبه میکند. اگر این مرکب شدن برای سال، ادامه پیدا کند، ارزش زمانی پول در آینده به صورت زیر محاسبه میشود.
روش محاسبه بالا برای زمانی مناسب است که مرکب شدن هر سال صورت بگیرد. اگر مرکب شدن را به صورت فصلی انجام دهیم، نرخ بهره تعلق گرفته برابر است و دوره مرکب شدن در سال رخ میدهد. به صورت مشابه، برای مرکب شدن ماهانه، هر در سال رخ میدهد. در نتیجه، معادله بالا به شکل زیر تغییر میکند.

مثال تناوب دوره مرکب شدن
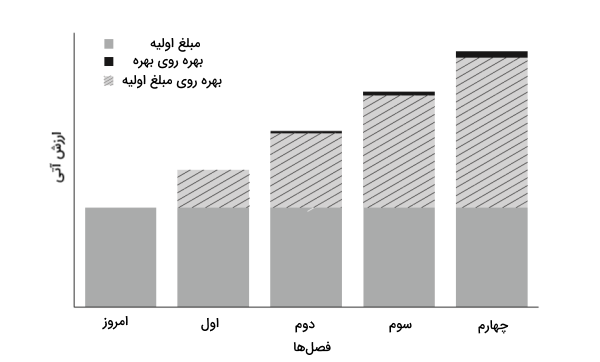
برای درک بهتر تناوب مرکب شدن پول به مثال زیر توجه کنید. فرض کنید که سپردهای به مبلغ ۱ میلیون تومان در بانک نگهداری میکنید که نرخ بهره مرکب سالانه آن برابر ۱۲ درصد است و به صورت فصلی مرکب میشود. یعنی در انتهای فصل اول، مانده حساب به صورت زیر بدست میآید.
۱٫۰۳۰ = ( ۰٫۰۳ + ۱ ) + ۱۰۰۰ = (( ۰٫۱۲/۴ ) + 1 ) 1000 = FV
مانده حساب در انتهای فصلهای دیگر را نیز با توجه به وضع شدن بهره بر مانده حساب، به روش مشابه بدست میآوریم.
۱۰۶۰٫۹۰ = ( ۰٫۰۳ + ۱ ) ۱۰۳۰٫۰۰ = FV
۱۰۹۲٫۷۳ = ( ۰٫۰۳ + ۱ ) ۱۰۶۰٫۹۰ = FV
۱۱۲۵٫۵۱ = ( ۰٫۰۳ + ۱ ) ۱۰۹۲٫۷۳ = FV
در نتیجه، در انتهای سال اول، مانده حساب برابر ۱۱۲۵٫۵۱ میلیون تومان است.
زمانی که نرخ بهره به صورت نرخ سالیانه اعلام شود اما مرکب شدن، بیشتر از یکبار در سال صورت بگیرد، نرخ بهره سالانه اعلام شده را «نرخ درصدی سالانه» (Annual Percentage Rate | APR) مینامند. توجه داشته باشید که هرچه تعداد دورههای مرکب شدن در یک سال، بیشتر باشد، ارزش زمانی پول در آینده زیادتر خواهد شد.
مثال مرکب شدن نرخ بهره
تحلیلگران عموماً رشد درآمد و سود سهام شرکتهای سهامی عام را مورد بررسی قرار میدهند. میتوان از این تخمینها برای پیشبینی و برنامهریزی استفاده کرد. شرکت «والت دیزنی» (Walt Disney) - یکی از بزرگترین شرکتهای رسانهای جهان - را در نظر بگیرید. در پایان سال مالی ۲۰۰۸، تحلیلگران انتظار داشتند که در بلندمدت نرخ رشد هر سال برابر ۱۲٫۱۹ درصد باشد. اگر EPS شرکت دیزنی برای سال مالی ۲۰۰۸ معادل ۲٫۲۷۸۸ دلار میبود و اگر شما با تحلیلگران همنظر میبودید، امکان پیشبینی EPS برای سالهای مالی آتی نیز وجود داشت.
- برای مثال، EPS تخمین زده شده برای سال ۲۰۰۹ میلادی به صورت زیر محاسبه میشود.
۲٫۵۵۶۶ = ( ۰٫۱۲۱۹ + ۱ ) ۲٫۲۷۸۸
- EPS تخمین زده شده برای سال ۲۰۱۰ میلادی
۲٫۸۶۸۲= ۲ ( ۰٫۱۲۱۹ + ۱ ) ۲٫۲۷۸۸
- EPS تخمین زده شده برای سال ۲۰۱۱ میلادی
۳٫۲۱۷۹ = ۳ ( ۰٫۱۲۱۹ + ۱ ) ۲٫۲۷۸۸
در نمودار زیر میتوانید تفاوت میان بهره مرکب و ساده را مشاهده کنید که نمایانگر رشد ۱۰۰۰ دلار با نرخ ۶ درصد با بکارگیری هر دو نوع نرخ بهره است.
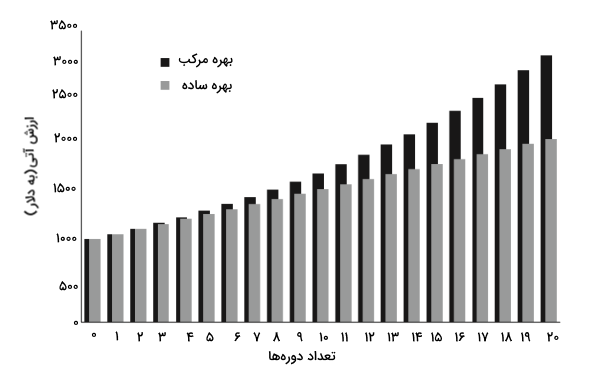
اگر برای محاسبه ارزش زمانی آتی پولی با توجه به ارزش فعلی آن و نرخ بهره در اکسل اقدام کرده باشید، ممکن است متوجه شوید که مقدار ارزش فعلی، منفی در نظر گرفته میشود زیرا در این معادله، این مقدار معادل «جریان خروجی» (Outflow) است. تغییر علامت ارزش زمانی پول فعلی در اغلب ماشینحسابهای مالی رخ میدهد.
نرخ بهره پیوسته چیست ؟
موارد بررسی شده تا به اینجا، شامل مرکب شدن مجزا یا دورهای بودهاند. در حالیکه، بسیاری از تراکنشهای مالی شامل نرخ بهره پیوسته هستند. در این نوع از مرکب شدن نرخ بهره، تناوب مرکب شدن به شدت افزایش مییابد زیرا نرخ بهره به صورت مداوم در حال مرکب شدن است. اگر مرکب شدن، بدون وقفه ادامه داشته باشد، از تابع نمایی، e، استفاده خواهیم کرد که معکوس لگاریتم طبیعی است. عامل مرکب کردن در مرکب سازی پیوسته به نرخ اعلام شده سالانه (یا همان APR) و تعداد سالها، احتیاج دارد.
فرمول محاسبه عامل مرکب کننده نرخ بهره پیوسته چیست؟
نرخ بهره پیوسته به صورت زیر محاسبه میشود.
در فرمول بالا:
- : «نرخ بهره سالیانه» (Annual Interest Rate)
- : تعداد سالها
مثال محاسبه عامل مرکب کننده نرخ بهره پیوسته
اگر نرخ بهره سالیانه ۱۰ درصد باشد و به صورت مداوم مرکب شود، عامل مرکب کننده برای یکسال، به صورت زیر محاسبه میشود.
برای دو سال، عامل مرکب کننده به صورت زیر محاسبه میشود.
برای ۱۰ سال، عامل مرکب کننده به صورت زیر محاسبه میشود.
فرمول محاسبه مرکب سازی پیوسته چیست؟
فرمول محاسبه ارزش آتی یک مبلغ با نرخ سود پیوسته به صورت زیر بدست میآید و عامل مرکب کننده همان است.
درواقع، مرکب شدن پیوسته حد تناوب مرکب شدن است.
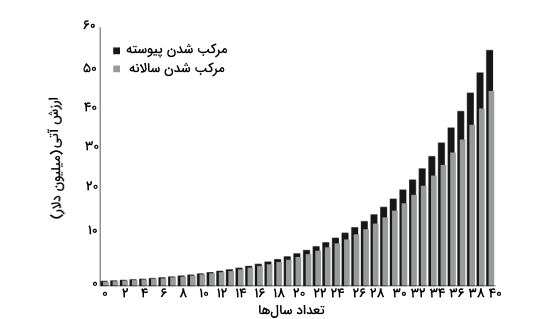
مثال مرکب شدن پیوسته و مرکب شدن مجزا
تصور کنید که ۱ میلیون دلار در حسابی به مدت ۵ سال نگهداری شود و نرخ بهره معادل ۱۰ درصد باشد. با مرکب شدن سالانه، مبلغ این سپرده به شکل زیر محاسبه میشود.
۱۶۱۰۵۱۰ =
با مرکب شدن پیوسته، ارزش زمانی پول پس از ۵ سال معادل محاسبه زیر خواهد بود.
۱۶۴۸۷۲۱ =
حال میتوانید تفاوت بین مرکبسازی سالانه و مرکب سازی پیوسته را مشاهده کنید. بعد از ۴۰ سال، تفاوت بین مرکب سازی پیوسته و مرکبسازی سالانه بیشتر از ۹ میلیون دلار خواهد بود.
تنزیل چیست؟
از تنزیل برای تبدیل ارزش زمانی پول در آینده به ارزش فعلی آن استفاده میکنیم.
فرمول تنزیل کردن چیست؟
در مواقعی، لازم است که ارزش فعلی پولی که در آینده به آن دست مییابیم را محاسبه کنیم. به همین علت، فرمول نگاشته شده در بالا را به شکل زیر مینویسیم.
با فرمول بالا میتوانیم ارزش زمانی پول کسبشده در آینده را برای زمان فعلی بدست آوریم. «تنزیل» (Discount)، همان فرایند تبدیل ارزش آتی مبلغ به ارزش فعلی آن است. مفهوم تنزیل یکی از مباحث مهم در مدیریت مالی است زیرا امکان مقایسه بین ارزشهای فعلی پرداختیهای آتی را فراهم میآورد.
هرچه تعداد دورههای تنزیل کردن یا بزرگتر باشد، عامل تنزیلکننده کوچکتر و ارزش فعلی کمتر میشود. هرچه نرخ بهره به ازای دوره، یا همان ، بزرگتر شود عامل تنزیل کوچکتر و ارزش زمانی پول در حال حاضر کمتر میشود. در سرمایهگذاری، نرخ تنزیل نشاندهنده هزینه فرصت مبالغ پول است. در این نوشتار، اغلب از حرف انگلیسی برای اشاره به نرخ بهره استفاده شده است. در متون مشابه ممکن است با حروف انگلیسی به معنی «نرخ بازدهی» (Required Rate of Return) یا حرف انگلیسی به معنی «هزینه سرمایه» (Cost of Capital) استفاده شده باشد. تمامی این موارد به مفهوم یکسان ارزش زمانی پول اشاره دارند.
مثال اول تنزیل
فرض کنید که قصد دارید تا پایان سال ششم، ۲۰ میلیون تومان ذخیره در حساب خود داشته باشید و همچنین فرض کنید که پولهای خود را امروز در حسابی قرار دادهاید که ۳ درصد بهره مرکب شده سالانه پرداخت میکند. برای رسیدن به هدف خود باید چه میزان پول را در این حساب قرار دهید؟
پاسخ مثال اول تنزیل
طبق دادههای مسئله، برای محاسبه به موارد زیر نیاز خواهیم داشت.
- ارزش زمانی پول در آینده: ۲۰ میلیون تومان
- تعداد دورهها یا n: شش
- نرخ بهره یا i: سه درصد
حال میخواهیم ارزش فعلی را محاسبه کنیم.
مثال دوم تنزیل
فرض کنید که در چنین روزی در ۴۰ سال بعد، تمایل به داشتن ۱۰۰ میلیون تومان در حساب بانکی خود داشته باشید. اگر پولهای خود را در حسابی با نرخ بهره ۵ درصد قرار دهید که به صورت سالانه مرکب شوند، میزان سپردهگذاری امروز شما باید به چه میزان باشد که به هدف خود دست پیدا کنید؟
پاسخ مثال دوم تنزیل
طبق دادههای مسئله، برای محاسبه به موارد زیر نیاز خواهیم داشت.
- ارزش زمانی پول در آینده: صد میلیون تومان
- تعداد دورهها: ۴۰
- نرخ بهره: پنج درصد
ارزش فعلی به صورت زیر محاسبه میشود.
تنزیل بیشتر از یک مقدار آتی برای تعیین ارزش یک سرمایهگذاری
برای مثال، ارزش یک سهام به سود انتظاری آینده آن بستگی دارد. همچنین، ارزش یک اوراق قرضه، نشاندهنده ارزش فعلی نرخ بهره و بازپرداخت اصل مبلغ انتظاری اوراق قرضه در آينده است.
سرمایهگذاری را در نظر بگیرید که در انتهای سال اول ۱۰ میلیون تومان، در انتهای سال دوم ۲۰ میلیون تومان و در انتهای سال سوم ۳۰ میلیون تومان پرداخت میکند. اگر نرخ تنزیل برابر ۵ درصد باشد، ارزش فعلی این سرمایهگذاری، امروز به چه میزان خواهد بود؟
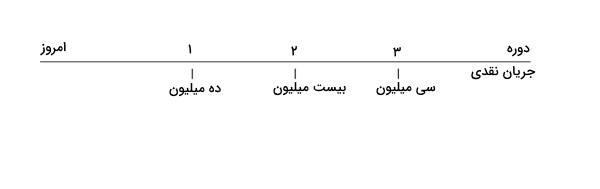
در این مسئله باید هر کدام از جریانهای نقدی را به صورت جداگانه تنزیل کنیم تا ارزش فعلی سرمایهگذاری انجام شده، محاسبه شود.
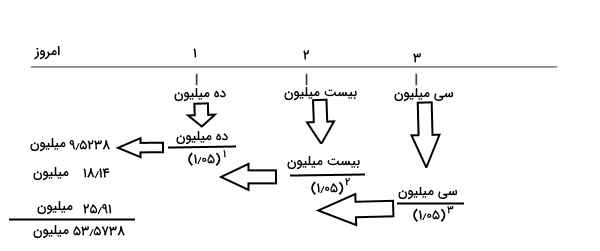
جهت کسب اطمینان از صحت انجام کار میتوانیم ارزش آتی هرکدام از این سه مبلغ را در انتهای سه سال محاسبه کنیم و سپس مبلغ بدست آمده را تنزیل کرده و ارزش فعلی آنرا بدست بیاوریم.
| ارزش آتی | جریان نقدی |
| ۱۱٫۰۲۵ میلیون | ۱۰ میلیون |
| ۲۱ میلیون | ۲۰ میلیون |
| ۳۰ میلیون | ۳۰ میلیون |
| ۶۲٫۰۲۵ میلیون | جمع |
با تنزیل کردن ۶۲٫۰۲۵ میلیون با نرخ ۵ درصد برای ۳ دوره، به ارزش فعلی ۵۳٫۵۷۳۸ دست پیدا میکنیم.
قانون ۷۲ چیست ؟
قانون ۷۲، روشی سریع و تقریبی برای تعیین ترکیبی از نرخ بهره و تعداد دوره مورد نیاز برای مضاعف کردن مبلغ مورد نظر شماست. برای مثال، اگر نرخ بهره، ۶ درصد باشد به ۱۲ دوره ( 12 = 6 ÷ 72 ) برای دوبرابر شدن مبلغ نیاز است. اگر برای محاسبه از ماشین حساب یا اکسل استفاده کنید، به رقم دقیقتر ۱۱٫۸۹۵۷ دوره میرسید.
میتوان از این قانون برای تعیین نرخ بهره برای تعداد معین دوره استفاده کرد. برای مثال، با چه میزان نرخ بهره میتوانید مقدار پول خود را در طی ۱۲ سال، دو برابر کنید؟ طبق قانون ۷۲، نرخ بهره باید معادل ۶ درصد یا به صورت دقیق برابر با ۵٫۹۴۶۳ درصد باشد.
| نرخ بهره | تعداد تقریبی دورهها | تعداد دقیق دورهها |
| ۳٪ | ۲۴٫۰۰ | ۲۳٫۴۵ |
| ۴٪ | ۱۸٫۰۰ | ۱۷٫۶۷ |
| ۵٪ | ۱۴٫۴۰ | ۱۴٫۲۵ |
| ۶٪ | ۱۲٫۰۰ | ۱۱٫۹۰ |
| ۷٪ | ۱۰٫۲۹ | ۱۰٫۲۴ |
| ۸٪ | ۹٫۰۰ | ۹٫۰۱ |
| ۹٪ | ۸٫۰۰ | ۸٫۰۴ |
| ۱۰٪ | ۷٫۲۰ | ۷٫۲۷ |
بررسی قانون ۷۲ از دید تخمین نرخ بهره
| تعداد دورهها | نرخ بهره تقریبی | نرخ بهره دقیق |
| ۳ | ۲۴٫۰۰٪ | ۲۵٫۹۹٪ |
| ۴ | ۱۸٫۰۰٪ | ۱۸٫۹۲٪ |
| ۵ | ۱۴٫۴۰٪ | ۱۴٫۸۷٪ |
| ۶ | ۱۲٫۰۰٪ | ۱۲٫۲۵٪ |
| ۷ | ۱۰٫۲۹٪ | ۱۰٫۴۱٪ |
| ۸ | ۹٫۰۰٪ | ۹٫۰۵٪ |
| ۹ | ۸٫۰۰٪ | ۸٫۰۱٪ |
| ۱۰ | ۷٫۲۰٪ | ۷٫۱۸٪ |
قانون ۶۹ چیست؟
قانون ۶۹، قانونی سریع و تقریبی برای تعیین ترکیب نرخ بهره و تعداد سالهای مورد نیاز (در صورت مرکب شدن پیوسته) برای دوبرابر کردن پول شماست. برای مثال، اگر نرخ بهره برابر ۶ درصد باشد و مبلغ به صورت پیوسته مرکب شود، تعداد سالهای مورد نیاز برای دوبرابر کردن پول ( 11٫۵ = 6 ÷ ۶۹ ) ۱۱ سال و نیم است. با محاسبه به روش مستقیم و بدون استفاده از این قانون به عدد ۱۱٫۵۵۲۴۵ میرسید.

لگاریتم طبیعی عدد ۲، برابر ۰٫۶۹۳۱۴۷ یا ۶۹ درصد است، به همین علت این قانون را قانون ۶۹ مینامند. این قانون را عموماً به صورت گرد شده و قانون ۷۰ خطاب میکنند.
مثالهای ارزش زمانی پول
جهت درک بیشتر معادلههای بیان شده در بالا، بهتر است چندین مثال را مورد بررسی قرار دهیم. برای یادگیری پیشنهاد میکنیم که قبل از رجوع به پاسخ سئوالها، خود تلاش کافی را برای بدست آوردن جوابها، انجام دهید.
مثال اول ارزش زمانی پول
فرض کنید که میخواهید یک واحد آپارتمانی را خریداری کنید که با قیمت ۸۵۰ میلیون تومان به فروش میرسد اما شما در حال حاضر توانایی پرداخت این مبلغ را ندارید. بااینحال، شما فکر میکنید که در ۴ سال آینده توانایی لازم را برای تهیه این مبلغ کسب میکنید. اگر تورم تاثیرگذار بر قیمت این واحد آپارتمانی به صورت سالانه برابر ۲۶ درصد باشد، قیمت انتظاری پس از گذشت ۴ سال، به چه میزان خواهد بود؟
مثال اول ارزش زمانی پول
طبق دادههای مسئله، ارزش فعلی این واحد آپارتمانی برابر ۸۵۰ میلیون و قرار است قیمت آن در طی ۴ سال، سالانه، ۲۶ درصد رشد - مطابق تورم - داشته باشد. با توجه به فرمولهای بیان شده، محاسبه را به شکل زیر انجام میدهیم.
قیمت این واحد مسکونی پس از ۴ سال با احتساب تورم، برابر دو میلیارد و صدو چهل و دو میلیون و چهارصد و دو هزار تومان، خواهد بود.
مثال دوم ارزش زمانی پول
فرض کنید خانم ضرغام، مبلغ ۶۰ میلیون تومان را در حسابی با نرخ بهره متغیر قرار داده باشد. در این حساب، نرخ بهره به صورت ماهانه، مرکب میشود. خانم ضرغام انتظار دارد که نرخ بهره سالانه برای ۳ ماهه اول معادل ۸ درصد، برای سهماهه دوم معادل ۹ درصد و برای ۳ماهه بعدی مجدداً برابر ۸ درصد، باشد. کل مبلغ جمعآوری شده در این حساب را پس از ۹ ماه بدست آورید.
پاسخ مثال دوم ارزش زمانی پول
مطابق دادههای مسئله، نرخ بهره سالانه معادل ۸ درصد و ۹ درصد است. یعنی نرخ بهره ماهانه معادل ۱۲/ ۰٫۰۸ و ۱۲/ ۰٫۰۹ خواهد بود. مبلغ محاسبه شده برای ۹ ماه به صورت زیر بدست میآید و معادل ۶۳ میلیون و هشتصد و پنجاه و یک هزار تومان است.
مثال سوم ارزش زمانی پول
فرض کنید که قرار است پس از ۵ سال، افزایش حقوقی به میزان ۱۰ میلیون تومان داشته باشید. شما ارزش زمانی فعلی این مبلغ را محاسبه کردهاید که برابر ۸ میلیون تومان است. شما از چه نرخی برای تنزیل استفاده کردهاید؟
پاسخ مثال سوم ارزش زمانی پول
برای محاسبه ارزش فعلی مبلغی از پول در آینده از فرمول زیر استفاده میکردیم.
یعنی
بنابراین،
در نتیجه، نرخ تنزیل برابر ۴٫۵۶ درصد بوده است.
مثال چهارم ارزش زمانی پول
فرض کنید که وامی به ارزش ۱۰۰ میلیون تومان از بانک دریافت کردهاید و باید در مهلت سررسید و پس از دو سال، ۱۲۰ میلیون تومان به بانک پرداخت کنید. نرخ بهره سالانه تعلق گرفته به این وام را بیابید.
پاسخ مثال چهارم ارزش زمانی پول
اگر ارزش آتی پول برابر ۱۲۰ میلیون تومان و ارزش فعلی آن معادل ۱۰۰ میلیون تومان و تعداد دورهها برابر ۲ باشد، از فرمول زیر استفاده میکنیم.
در نتیجه، با جایگذاری، معادله به شکل زیر تغییر میکند.
همانطور که مشاهده کردید، نرخ بهره وضع شده بر این وام معادل ۹٫۵۴۵ درصد بوده است.
مثال پنجم ارزش زمانی پول
فرض کنید که شما در ابتدای هر ماه، مبلغ ۳ میلیون و پانصد هزارتومان به حسابی که نرخ بهره آن ۶ درصد است، پرداخت میکنید و مبالغ این حساب به صورت ماهانه مرکب میشوند. کل مبلغ جمعآوری شده در حساب در انتهای ماه بیست و پنجم، چقدر است؟
پاسخ مثال پنجم ارزش زمانی پول
نرخ بهره ماهیانه، معادل ۰.۵ درصد است. اولین مبلغ پرداختی یا سه میلیون و پانصد هزار تومان را در نظر بگیرید. ارزش آتی آن پس از ۲۵ ماه برابر با است. مبلغ پرداختی دوم که ماه بعد پرداخت میشود، ۲۴ ماه تا سررسید فرصت دارد. به همینصورت، تنها یک ماه بهره به آخرین سپرده تعلق میگیرد و کل مبلغ در انتهای ۲۵ ماه به شکل زیر محاسبه می شود.

در اینجا یک دنباله هندسی را داریم که در آن جمله اول برابر و تعداد جملهها معادل ۲۵ است. قدر نسبت این دنباله، باعث کاهش مقدار جملات میشود.
با بکارگیری فرمول زیر
میتوانیم محاسبه را به شکل زیر انجام دهیم و مبلغ گردآوری شده پس از ۲۵ ماه معادل ۹۲ میلیون و ۹۰۰ هزار تومان خواهد بود.
سخن پایانی
برای ارزشگزاری یک سرمایهگذاری نیاز به تعیین نوع آن، مقدار و زمانبندی جریانهای نقدی مربوط به سرمایهگذاری دارید. زمانی که مقدار و زمانبندی جریانهای نقدی دارایی را تخمین بزنیم، میتوانیم با استفاده از روابط ریاضی ارزش زمانی پول را بسنجیم.













سلام و خسته نباشید. بابت مطلب مفید و کاملتون خیلی خیلی ممنونم.و خواهش میکنم ادامه بدین و مطالب بیشتری بذارید که واقعا کارتون عالی هست. بازم ممنونم.
سلام وسپاس از مطلبی خوبی که ارائه کردید. با احترام
خیلی مثال ها مفید بودن ممنونم