ارتعاشات اجباری نامیرا با تحریک نیروی هارمونیک – از صفر تا صد

ارتعاشات اجباری در یک سیستم مکانیکی یا سازهای هنگامی رخ میدهد که در حین ارتعاشات، انرژی خارجی به سیستم اعمال شود. این انرژی خارجی میتواند به شکل یک نیروی خارجی یا حتی تحریک جابجایی خود را نشان دهد. همچنین، نیروی خارجی یا تحریک جابجایی میتواند به صورت یکی از انواع هارمونیک، غیر هارمونیک، متناوب، نامتناوب یا تصادفی باشد. پاسخ یک سیستم به تحریک هارمونیک را پاسخ هارمونیک مینامیم. از طرفی، پاسخ یک سیستم دینامیکی به تحریک نامتناوب و ناگهانی نیز تحریک گذرا نامیده میشود. مدت زمانی که تحریک نامتناوب به طول میانجامد، ممکن است کوتاه یا بلند باشد. در این مقاله، ارتعاشات اجباری نامیرا با تحریک نیروی هارمونیک را بررسی خواهیم کرد.
معادله حرکت در ارتعاشات اجباری نامیرا
نیروی $$\large F(t)$$ به سیستم شکل زیر وارد میشود که متشکل از جرم، فنر و میراگر است.
با کمک قانون دوم نیوتن، معادله حرکت را برای این سیستم مینویسیم.
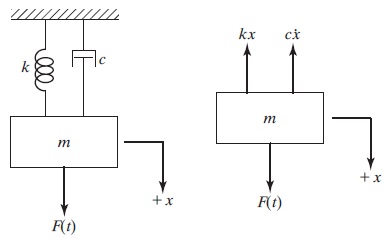
$$\large m\ddot{x} \:+\: c\dot{x} \:+\: kx \:=\: F(t)$$
(رابطه ۱)
از آنجایی که معادله بالا غیرهمگن است، پاسخ عمومی آن ($$\large x(t)$$) به صورت مجموع پاسخ همگن ($$\large x_h(t)$$) و پاسخ خصوصی ($$\large x_p(t)$$) به دست میآید. پاسخ همگن، همان پاسخ معادله زیر است که ارتعاشات آزاد را نشان میدهد.
$$\large m\ddot{x} \:+\: c\dot{x} \:+\: kx \:=\:0$$
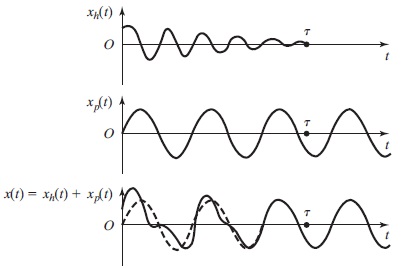
همانطور که میدانید، ارتعاشات آزاد تحت هرگونه وضعیت میرایی (زیر میرایی، میرایی بحرانی و فوق میرایی) و با شرایط اولیه مختلف، پس از سپری شدن مدت زمان مشخصی، از حرکت باز میایستد. بنابراین رابطه ۱، ناگهان به پاسخ خصوصی $$\large x_p(t)$$ تبدیل میشود که نشان دهنده ارتعاشات حالت پایدار است. حرکت حالت پایدار تا مادامی ادامه دارد که تابع نیرو، وجود داشته باشد. تغییر پاسخهای همگن، خصوصی و عمومی با زمان برای یک سیستم فرضی در شکل زیر رسم شده است. همانطور که مشاهده میکنید، پس از سپری شدن مدتی (تا رسیدن نمودار به زمان $$\large \tau$$)، $$\large x_h(t)$$ از بین رفته و $$\large x(t)$$ با $$\large x_p(t)$$ برابر میشود.
قسمتی از حرکت که به دلیل میرایی از بین میرود (بخش ارتعاشات آزاد)، قسمت گذرا نامیده میشود. سرعت از بین رفتن حرکت گذرا، به مقدار پارامترهای $$\large c$$، $$\large k$$ و $$\large m$$ وابسته است. در ادامه این مقاله، اثر ارتعاشات اجباری نامیرا در سیستمهایی که با نیروی هارمونیک تحریک میشوند، دنبال خواهد شد.
پاسخ سیستم در ارتعاشات اجباری نامیرا با تحریک نیروی هارمونیک
اگر نیروی $$\large F(t) =F_0 \cos \omega t$$ به جرم $$\large m$$ در یک سیستم نامیرا وارد شود، معادله حرکت جدید به صورت زیر است.
$$\large m\ddot{x} \:+\: kx \:=\: F_0 \cos \omega t$$
(رابطه ۲)
پاسخ همگن این معادله را مینویسیم.
$$\large x_h(t) \:=\: C_1\cos \omega_n t \:+\: C_2 \sin \omega_n t$$
در عبارت بالا، $$\large \omega_n =\sqrt {k/m}$$ فرکانس طبیعی سیستم است. از آنجایی که نیروی تحریک ($$\large F(t)$$) هارمونیک است، پاسخ عمومی $$\large x_p(t)$$ نیز هارمونیک بوده و فرکانس آن نیز برابر $$\large \omega$$ است. پاسخ خصوصی به شکل زیر است.
$$\large x_p(t) \:=\: X \:\cos \omega t$$
(رابطه ۳)
در عبارت بالا، $$\large X$$ ثابت است و بیشترین دامنه $$\large x_p(t)$$ را نشان میدهد. با ادغام رابطههای ۲ و ۳ و مرتب کردن آن برحسب $$\large X$$ به رابطه زیر میرسیم.
$$\large X\:=\: \frac {F_0} {k \:-\: m\omega^2} \:=\: \frac {\delta _{st}} {1 \:-\: (\frac {\omega} {\omega_n})^2}$$
(رابطه ۴)
عبارت $$\large \delta _{st}= F_0/k$$ جابجایی جرم $$\large m$$، تحت نیروی $$\large F_0$$ است و از آنجایی که $$\large F_0$$ یک نیروی ثابت (استاتیک) به حساب میآید، جابجایی استاتیکی نیز خوانده میشود. از این رو، پاسخ کلی رابطه ۲ به صورت زیر خواهد بود.
$$\large x(t) \:=\: C_1 \cos \omega_n t \:+\: C_2 \sin \omega_n t \:+\: \frac {F_0} {k\:-\: m\omega^2} \cos \omega t$$
برای یافتن ضریبهای ثابت، شرایط اولیه را به صورت $$\large x(t=0) =x_0$$ و $$\large \dot{x}(t=0) =\dot{x}_0$$ تعریف میکنیم.
$$\large C_1\:=\: x_0\:-\: \frac {F_0} {k\:-\: m\omega^2} \\~\\
\large C_2\:=\: \frac {\dot {x}_0} {\omega_n}$$
حالا میتوانیم پاسخ کلی را بازنویسی کنیم.
$$\large x(t) \:=\: (x_0 \:-\: \frac {F_0} {k \:-\: m\omega^2}) \cos \omega_n t \:+\: (\frac {\dot {x} _0} {\omega_n}) \sin \omega_n t \\~\\
\large + (\frac {F_0} {k \:-\: m\omega^2}) \cos \omega t$$
(رابطه ۵)
همچنین، ماکزیمم مقدار $$\large X$$ در رابطه ۴ نیز برابر با عبارت زیر است.
$$\large \frac {X} {\delta _{st}} \:=\: \frac {1} {1\:-\: (\frac {\omega} {\omega_n})^2}$$
(رابطه 6)
مقدار $$\large X/ \delta_ {st}$$ نشاندهنده نسبت اندازه حرکت دینامیکی به اندازه حرکت استاتیکی است و ضریب بزرگنمایی (Magnification Factor) یا نسبت دامنه (Amplitude Ratio) نام دارد. تغییرات نسبت دامنه برحسب تغییرات نسبت فرکانس ($$\large r= \omega/ \omega_n$$) در شکل زیر قابل مشاهده است. با توجه به این شکل، پاسخ سیستم میتواند سه حالت مختلف داشته باشد.
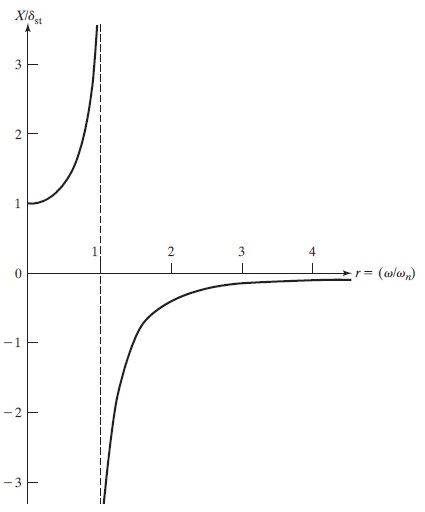
حالت اول زمانی رخ میدهد که $$\large 0<\omega/ \omega_n <1$$ برقرار باشد. در این حالت، مخرج کسر در رابطه 6، مثبت بوده و پاسخ آن مانند رابطه ۳ و بدون تغییر خواهد بود. شکل زیر را در نظر بگیرید. پاسخ هارمونیک سیستم $$\large x_p(t)$$ با نیروی خارجی همفاز است.
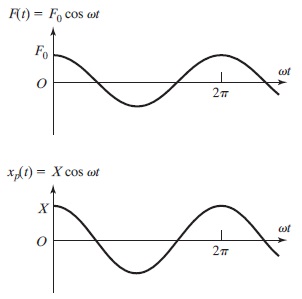
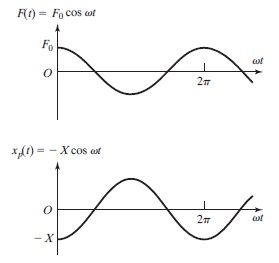
در حالت دوم، رابطه $$\large \omega/ \omega_n >1$$ برقرار است. در نتیجه، مخرج کسر در رابطه 6 منفی میشود و پاسخ حالت ماندگار به صورت زیر خواهد بود.
$$\large x_p(t) \:=\: -\:X \cos \omega t$$
در رابطه بالا، دامنه حرکت $$\large X$$ طوری تعریف میشود که همواره مثبت باشد.
$$\large X\:=\: \frac {\delta_ {st}} {(\frac {\omega} {\omega_n})^2 \:-\:1}$$
(رابطه 7)
تغییرات $$\large F(t)$$ و $$\large x_p(t)$$ را نسبت به زمان، در شکل زیر ملاحظه میکنید. از آنجایی که $$\large F(t)$$ و $$\large x_p(t)$$ مقداری مثبت دارند، پاسخ آنها $$\large 180^ \circ$$ از نیروی خارجی عقبتر است. علاوه بر آن، اگر $$\large \omega/ \omega_n \rightarrow \infty$$، آنگاه $$\large X \rightarrow 0$$ برقرار خواهد بود. بنابراین، پاسخ سیستم به یک نیروی هارمونیک با فرکانس زیاد، نزدیک به صفر است.
اما در حالت سوم که به صورت $$\large \omega/ \omega_ n=1$$ تعریف میشود، اندازه $$\large X$$ در رابطههای 6 و 7، بینهایت خواهد شد. این حالت که در آن، فرکانس نیرو $$\large \omega$$ با فرکانس طبیعی سیستم $$\large \omega_n$$ برابر است، رزونانس یا تشدید نام دارد. برای یافتن پاسخ سیستم در این حالت، رابطه 5 را بازنویسی میکنیم.
$$\large x(t) \:=\: x_0 \cos \omega _nt \:+\: \frac {\dot{x} _0} {\omega _n} \sin \omega _nt \:+\: \delta _{st} [\frac {\cos \omega t\:-\: \cos \omega _nt} {1\:-\: (\frac {\omega} {\omega _n})^2}]$$
از آنجایی که عبارت سمت راست در رابطه بالا، در حالت $$\large \omega =\omega _n$$، تعریف نشده خواهد بود، برای محاسبه مقدار حدی آن، از قاعده هوپیتال استفاده میکنیم.
$$\large \lim_{\omega \rightarrow \omega_n} [\frac {\cos \omega t\:-\: \cos \omega _nt} {1\:-\: (\frac {\omega} {\omega _n})^2}] \:=\: \lim_{\omega \rightarrow \omega_n} [\frac {\frac {\text {d}}{\text {d} \omega} (\cos \omega t\:-\: \cos \omega _nt)} {\frac {\text {d}}{\text {d} \omega}(1\:-\: (\frac {\omega} {\omega _n})^2)}] \\~\\
\large =\: \lim_{\omega \rightarrow \omega_n} [\frac {t\sin \omega t} {2\frac {\omega} {\omega_n^2}}] \:=\: \frac {\omega _nt} {2} \sin \omega _nt$$
حالا میتوانیم پاسخ سیستم را به صورت کامل بنویسیم.
$$\large x(t) \:=\: x_0 \cos \omega _nt \:+\: \frac {\dot{x} _0} {\omega _n} \sin \omega _nt \:+\: \frac {\delta _{st} \omega _nt} {2} \sin \omega _nt$$
از این رابطه متوجه میشویم که در رزونانس، مقدار $$\large x(t)$$ تا بینهایت افزایش مییابد. آخرین عبارت در رابطه بالا را میتوانید در شکل پایین مشاهده کنید. دامنه رزونانس به صورتی خطی با زمان در حال زیاد شدن است.
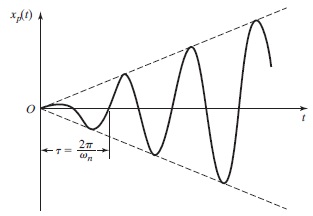
پاسخ نهایی ارتعاشات اجباری نامیرا با تحریک نیروی هارمونیک
پاسخ نهایی سیستم مربوط به رابطه ۵ را میتوانیم به صورت زیر بنویسیم.
$$\large x(t) \:=\: A \cos (\omega _nt \:-\: \phi) \:+\: \frac {\delta _{st}} {1\:-\: (\frac {\omega} {\omega_n})^2} \cos \omega _t ~~~ ~~~ ~~~ \frac {\omega} {\omega_n} <1$$
(رابطه ۸)
$$\large x(t) \:=\: A \cos (\omega _nt \:-\: \phi) \:+\: \frac {\delta _{st}} {-\:1\:+\: (\frac {\omega} {\omega_n})^2} \cos \omega _t ~~~ ~~~ ~~~ \frac {\omega} {\omega_n} >1$$
(رابطه ۹)
بنابراین حرکت کلی به صورت مجموع دو منحنی کسینوسی با فرکانسهای مختلف نشان داده میشود. در رابطههای ۸ و ۹، فرکانس نیرو ($$\large \omega$$) به ترتیب از فرکانس طبیعی کوچکتر و بزرگتر است. پاسخ کلی سیستم در شکل زیر نشان داده شده است.
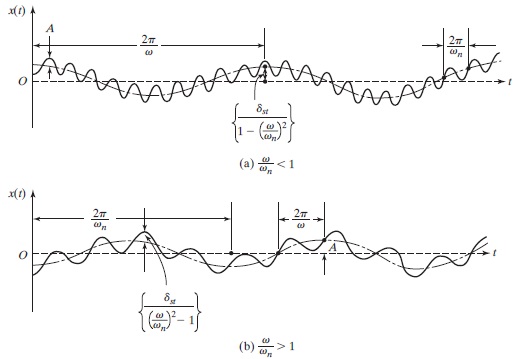
پدیده ضربان در ارتعاشات اجباری نامیرا
اگر فرکانس نیرو نزدیک به فرکانس طبیعی باشد (و نه مساوی با آن)، پدیدهای رخ میدهد که به آن ضربان (Beating) گفته میشود. این نوع از ارتعاشات اجباری نامیرا را میتوان با در نظر گرفتن پاسخی به صورت رابطه ۵ توضیح داد.
اگر شرایط اولیه را به صورت $$\large x_0\:=\: \dot {x}_0 \:=\:0$$ فرض کنیم، رابطه ۵ به شکل زیر نوشته میشود.
$$\large x(t)\:=\: \frac {(F_0/m)} {\omega_n ^2\:-\: \omega ^2} (\cos \omega t\:-\: \cos \omega _nt) \\~\\
\large =\: \frac {(F_0/m)} {\omega_n ^2\:-\: \omega ^2} [2\sin \frac {\omega_n \:+\: \omega} {2} t.\:\sin \frac {\omega_n \:-\: \omega} {2} t]$$
حالا فرض کنیم فرکانس نیرو اندکی از فرکانس طبیعی کمتر باشد.
$$\large \omega_n \:-\:\omega \:=\: 2\epsilon$$
مقدار مثبت بسیار کوچک را با $$\large \epsilon$$ نشان دادهایم.
$$\large \omega \:+\: \omega_n \:=\: \omega \:+\: \omega \:+\: \epsilon \:\cong\: 2\omega$$
اکنون اگر طرفین دو رابطه اخیر را در هم ضرب کنیم، رابطه زیر به دست میآید.
$$\large \Rightarrow \omega_n ^2\:-\: \omega^2 \:=\: 4\epsilon \omega$$
به این ترتیب میتوانیم مجدداً پاسخ $$\large x(t)$$ را بنویسیم.
$$\large x(t)\:=\: (\frac {F_0/m} {2\epsilon \omega} \sin \epsilon t) \:\sin \omega t$$
از آنجایی که $$\large \epsilon$$ مقداری بسیار کوچک است، تابع $$\large \sin \epsilon t$$ به کُندی تغییر کرده و دوره تناوبی بزرگ و برابر با $$\large 2\pi/ \epsilon$$ خواهد داشت. به همین دلیل، رابطه بالا ارتعاشات اجباری نامیرا با دوره تناوب $$\large 2\pi/ \epsilon$$ و دامنهای متغیر را نشان میدهد. از طرفی دیگر، همانطور که در شکل زیر نیز مشهود است، در مدت زمانی که منحنی $$\large \sin \epsilon t$$ فقط یک سیکل را کامل میکند، منحنی $$\large \sin \omega t$$ چند سیکل نوسان میکند. مدت زمان بین هر دو دامنه صفر یا هر دو دامنه ماکزیمم، دوره ضربان نام دارد و با نماد $$\large \tau_b$$ تعریف میشود.
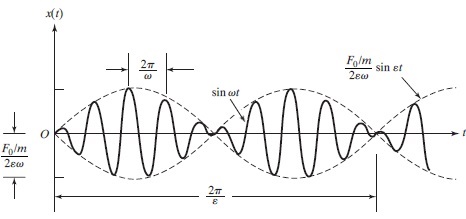
$$\large \tau_b \:=\: \frac {2\pi} {2\epsilon} \:=\: \frac {2\pi} {\omega _n\:-\: \omega}$$
از این رو، فرکانس ضربان نیز برابر با $$\large \omega _b=2 \epsilon= \omega _n- \omega$$ است.
مثال: صفحه نگهدارنده یک پمپ
سؤال: یک پمپ رفت و برگشتی به وزن $$\large 150\: lb$$ در مرکز صفحه فولادی قرار گرفته است. طول و عرض این صفحه به ترتیب $$\large 100$$ و $$\large 20$$ اینچ بوده و ضخامت آن نیز $$\large 0.5$$ اینچ است. در حین روشن بودن پمپ، این صفحه در معرض یک نیروی هارمونیک قرار میگیرد که اندازه این نیرو برابر با $$\large F(t)\:=\: 50\cos 62.832 t$$ و با واحد $$\large lb$$ است. دامنه ارتعاشات اجباری نامیرا در صفحه را بیابید.
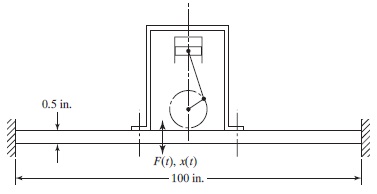
پاسخ: این صفحه را میتوانیم مانند تیر دو سر گیردار و با مدول یانگ $$\large E\:=\: 30 \times 10^6 \:psi$$ مدلسازی کنیم. ابتدا ممان اینرسی سطح را به دست میآوریم.
$$\large I\:=\: \frac {1} {12} (20) (0.5)^3 \:=\: 0.2083\: in^4$$
برای به دست آوردن سفتی خمشی (Bending Stiffness) از رابطه زیر استفاده میکنیم.
$$\large k\:=\:\frac {192EI} {l^3} \:=\: \frac {192 (30 \times 10^6) (0.2083)} {(100)^3} \:=\: 1200.0 \:lb/in$$
دامنه پاسخ هارمونیک با کمک رابطه ۴ محاسبه میشود. با جایگذاری مقادیر مختلف، $$\large X$$ به دست میآید.
$$\large F_0\:=\: 50\: lb ~~~ ~~~ ~~~ m\:=\: 150/ 386.4\: lb-sec^2 /in \\~\\
\large k\:=\: 1200 lb/in ~~~ ~~~ ~~~ \omega\:=\: 62.832\: rad/s \\~\\
\large X\:=\: \frac {F_0} {k\:-\: m\omega^2} \:=\: \frac {50} {1200\:-\: (150/386.4) (62.832)^2} \\~\\
\large \Rightarrow ~~~ X\:=\:-\: 0.1504 \:in$$
علامت منفی نشان میدهد که پاسخ $$\large x(t)$$ مربوط به صفحه فولادی، نسبت به تحریک $$\large F(t)$$ اختلاف فاز دارد.
مثال: تعیین جرم با استفاده از پاسخ هارمونیک در ارتعاشات اجباری نامیرا
سؤال: به یک سیستم جرم و فنر، نیروی هارمونیک به بزرگی $$\large 30 \:N$$ و فرکانس $$\large 20 \:Hz$$ وارد میشود. ثابت فنر برابر $$\large 5,000 \:N/m$$ است و جرم با دامنه $$\large 0.2 \:m$$ نوسان میکند. با فرض اینکه ارتعاشات اجباری نامیرا از حالت سکون ($$\large x_0 =\dot {x}_ 0=0$$) شروع شده باشد، جرم سیستم را تعیین کنید.
پاسخ: پاسخ ارتعاشات اجباری نامیرا در سیستم را میتوانیم با کمک رابطه ۵ به دست آوریم. کافی است از شرایط اولیه داده شده در صورت سؤال استفاده کنیم.
$$\large x(t) \:=\: \frac {F_0} {k\:-\: m\omega^2} (\cos \omega t\:-\: \cos \omega _nt)$$
با کمک روابط مثلثاتی و بازنویسی رابطه بالا، به شکل جدیدی برای $$\large x(t)$$ میرسیم.
$$\large x(t) \:=\: \frac {2F_0} {k\:-\: m\omega^2} \sin \frac {\omega_n \:+\: \omega} {2}t \sin \frac {\omega_n \:-\: \omega} {2}t$$
از طرفی، دامنه این ارتعاشات اجباری نامیرا معلوم و برابر با $$\large 0.2 \:m$$ است.
$$\large \frac {2F_0} {k\:-\: m\omega^2} \:=\: 0.2$$
اکنون میتوانیم جرم سیستم را با داشتن سایر متغیرها، محاسبه کنیم.
$$\large F_0 \:=\: 30\:N ~~~ ~~~ ~~~ \omega \:=\: 20 \:Hz \:=\: 125.665\: rad/s \\~\\
\large k\:=\: 5,000\: N/m \\~\\
\large \Rightarrow ~~~ \frac {2(30)} {5000 \:-\: m(125.664)^2} \:=\: 0.2 \\~\\
\large \Rightarrow ~~~ m\:=\: 0.2976 \:kg$$
اگر به مباحث مرتبط در زمینه مکانیک و ارتعاشات علاقهمند هستید، آموزشهای زیر به شما پیشنهاد میشوند:
- مجموعه آموزش های مهندسی مکانیک
- مجموعه آموزشهای نرمافزارهای مهندسی مکانیک
- آموزش ارتعاشات مکانیکی همراه با حل مثال در متلب (MATLAB)
- آموزش ارتعاشات مکانیکی (مرور و حل تست کنکور ارشد)
- ژیروسکوپ – از صفر تا صد
- رزونانس – به زبان ساده
- ارتعاشات مکانیکی — بخش سوم: سیستمهای دو درجه آزادی
^^










سلام این پدیده در دینامیک خاک هم مطرح است اما کتاب مکانیک داس جواب پدیده ضربان را غ ق ق دانسته.چرا؟