کسرهای تبدیل استوکیومتری – به زبان ساده + توضیح کامل و مثال
کسرهای تبدیل در تمامی علوم کاربرد دارند. این کسرها برای تبدیل یک واحد اندازهگیری به واحدی دیگر و برای حل مسائل به کار میروند. در شیمی، کسرهای تبدیل استوکیومتری اغلب برای موازنه معادله واکنشهای شیمیایی و حل مسائل استوکیومتری استفاده میشوند. برای موازنه معادله شیمیایی و حل این مسائل، باید با مفاهیمیمانند اتم، عنصر، عدد جرمی، جرم مولی، عدد اتمی، مول و غیره آشنا باشیم و مفاهیم پایه ریاضیات مانند ضرب و تقسیم را به درستی به کار گیریم. مهمترین کسرهای تبدیل استوکیومتری آنهایی هستند که مقادیر مول را به مول، گرم و لیتر تبدیل میکنند. در این مبحث از مجله فرادرس به بررسی چگونگی استفاده از روابط استوکیومتری موجود در معادلات شیمیایی و روش موازنه آنها و همچنین به دست آوردن مقادیر مختلف ترکیبات موجود در واکنش با کسرهای تبدیل استوکیومتری میپردازیم. با این روشها میتوانیم مقدار دقیق واکنش دهندهها و فراوردهها را به دست آوریم.
- میآموزید چگونه کسرهای تبدیل را در حل مسائل شیمی بهکار ببرید.
- با سه قانون بنیادی شیمی در محاسبات استوکیومتری آشنا میشوید.
- یاد خواهید گرفت ضرایب و کسرهای تبدیل را بهدرستی از هم تمییز دهید.
- نحوه تبدیل بین واحدهای مول، جرم و حجم را تمرین میکنید.
- فرایند استخراج و تکمیل فرمول تجربی و مولکولی را بهصورت مرحلهای میآموزید.
- کاربرد ضرایب و نسبتهای عددی واکنشها را در مثالهای واقعی بهکار میگیرید.


در شیمی، واکنشهای شیمیایی با فرمولهایی حاوی نماد عناصر و ترکیبات و مقادیر آنها نشان داده میشوند.واکنش دهندهها در سمت چپ و فراوردهها در سمت راست معادله نوشته میشوند و دو سمت معادله با فلشی یک یا دوجهتی به یکدیگر مربوط میشوند. در این واکنشهای شیمیایی، تعداد اتمهای هر دو طرف معادله با یکدیگر برابر است تا قانون بقای جرم رعایت شود. کسرهای تبدیل استوکیومتری، ضرایب تبدیلی مناسب برای بهدست آوردن مقادیری از هر عنصر و مولکول در واکنش در واحد مورد نظر هستند. در ادامه این مطلب درباره مفهوم استوکیومتری و اهمیت این کسرهای تبدیل در آن مطالعه میکنیم. همچنین مبانی استوکیومتری را میآموزیم و براساس آنها یاد میگیریم چگونه واکنشهای شیمیایی را موازنه کنیم. سپس با انواع کسرهای تبدیل استوکیومتری آشنا شده و درباره واکنش دهنده محدود کننده و بازده نظری واکنش توضیح میدهیم. با مطالعه این مطلب تا انتها، با این مفاهیم پایهای مهم و مثالهای آن آشنا شوید.
استوکیومتری چیست؟
استوکیومتری مطالعه روابط کمی مواد شرکت کننده در واکنش شیمیایی است. معادله شیمیایی درست، معادلهای است که موازنه شده باشد. معادله متوازن، نشان میدهد که چه واکنش دهندههایی با چه مقادیری باهم ترکیب میشوند تا چه فراوردههایی را تشکیل دهند. همچنین در معادله موازنه شده، روابط عددی بین واکنش دهندهها و محصولات نیز به درستی نشان داده میشود. این روابط عددی به عنوان استوکیومتری شناخته میشوند. استوکیومتری شاخهای از شیمی است که شامل استفاده از روابط بین واکنش دهندهها یا محصولات در واکنش شیمیایی برای تعیین دادههای کمی مورد نظر است.
یکی از بحثهای مهم شیمی، استوکیومتری است. استوکیومتری در واقع مطالعه مقادیر واکنش دهندهها و فراوردهها در واکنش شیمیایی است. این کلمه از دو قسمت یونانی به نام استوکیون (عنصر) و مترون (اندازه) گرفته شده است. بنابراین استوکیومتری بهطور لغوی به معنی اندازهگیری عناصر است. استوکیومتری گاهی وقتها به نام روابط جرمی بین اجزای واکنش نیز شناخته میشود. برای استفاده از روابط و کسرهای تبدیل استوکیومتری، نیاز است ابتدا روابط بین واکنش دهندهها و فراوردهها و دلیل وجود این روابط درک شود. درک این روابط نیز نیاز به فهم روش انجام موازنه واکنشهای شیمیایی را دارد.
مبانی استوکیومتری
برای استفاده از استوکیومتری در محاسبات مربوط به واکنشهای شیمیایی، مهم است که ابتدا روابط موجود بین فراوردهها و واکنش دهندهها و دلایل وجود آنها را درک کنیم که این امر نیازمند فهم تعادل واکنشها است. روابط جرمی بین اجزای واکنش بر سه اصل مهم بنا شدهاند.
اگر این اصول رعایت شوند، امکان پیشبینی و محاسبات معتبر برای واکنش شیمیایی فراهم میشود.
- قانون حفظ جرم: در این قانون گفته میشود که جرم واکنش دهندهها و فراوردهها برابر است.
- قانون نسبتهای متعدد: در این قانون گفته میشود که عناصر در واکنش، با نسبت ثابتی با اعداد صحیح ترکیب میشوند.
- قانون ترکیب ثابت: در این قانون گفته میشود تمام نمونههای ترکیب شیمیایی مشخص دارای عنصر یکسانی هستند.
یادگیری شیمی پایه دهم با فرادرس
یکی از پایهایترین مباحث شیمی مسائل استوکیومتری و موازنه مواد است. یادگیری این مباحث از اهمیت بالایی برخوردار است. برای یادگیری موازنه مواد باید با مفاهیمی مانند جرم اتمی، ساختار اتم، پیوند کووالانسی و استوکیومتری واکنش آشنا شد. این مفاهیم به طور کامل و با زبانی ساده در مجموعه آموزش پایه دهم و در بخش آموزش شیمی پایه دهم آموزش داده شدهاند. همچنین مثالهای فراوان برای تمرین بیشتر این مباحث در این آموزشها آورده شده است. پیشنهاد میکنیم برای یادگیری بیشتر این مباحث به مجموعه فیلم آموزش پایه دهم خصوصا فیلم آموزش شیمی ۱ پایه دهم مراجعه کنید. در فهرست زیر به چند نمونه از این آموزشها اشاره کردهایم.
همچنین با مراجعه به صفحههای زیر میتوانید به آموزشهای بیشتر در این زمینه دسترسی داشته باشید.
- فیلم آموزش موازنه انرژی و مواد
- فیلم آموزش شیمی عمومی ۱ و ۲ به همراه مرور و حل مساله
- فیلم آموزش شیمی عمومی جامع و با مفاهیم کلیدی
اهمیت کسرهای تبدیل در استوکیومتری
فرمولهای عناصر و ترکیبات باید در طول واکنش تغییر کنند، اما مقدار نسبی هر اتم یا یون درگیر در واکنش باید ثابت بماند. زیرنویسهایی که در فرمول شیمیایی موجود هستند، به ماهیت عنصر، یون یا ترکیب مربوطه وابستهاند و نمیتوان آنها را تغییر داد تا قانون بقای ماده رعایت شود. این قانون ایجاب میکند که در طی واکنش شیمیایی هیچ ذرهای تولید یا نابود نشود. در نتیجه، بیشتر واکنشها باید موازنه شوند تا هرگونه تفاوت نسبی بین فرمولهای واکنش دهندهها و محصولات درگیر در واکنش در نظر گرفته شود.
علاوه بر این، ضرایب استوکیومتری نسبت حضور واکنش دهندهها را به فراوردهها نشان میدهند. تعداد اتمها یا مولکولهای محصول تولید شده، نسبت به مقدار واکنش دهندههای مصرف شده، توسط این ضرایب تعیین میشوند. با استفاده از این دو پارامتر میتوان مقادیر جرم، حجم و ... ترکیبات و اتمهای شرکتکننده در واکنش را به وسیله کسرهای تبدیل استوکیومتری به دست آورد. استوکیومتری، که به بررسی مقدار مواد در حین واکنشهای شیمیایی میپردازد، یکی از مفاهیم اساسی در شیمی بهشمار میرود. بنابراین،کسرهای تبدیل استوکیومتری موجود در واکنش مقادیر شیمیایی مهمی هستند.
ضرایب و نسبتهای استوکیومتری در شیمی مانند دستوری برای پخت مواد غذایی که نسبت مواد را تعیین میکند، روند انجام واکنش تا رسیدن به فراوردهها را کمیسازی میکنند.
مفاهیم و مسائل رایج استوکیومتری
مقادیر کمی در مسائل استوکیومتری، به صورت اتم، گرم، مول و واحدهای اندازهگیری حجم بیان میشوند. به همین علت، نیاز است که تبدیلهای واحد ریاضیات به خوبی در این مسائل بهکار گرفته شوند. در ادامه به توضیح مهمترین مفهوم استوکیومتری که واحد اندازهگیری ذرات (مول) است میپردازیم مسائل رایج کسرهای تبدیل در استوکیومتری را بیان میکنیم.
مفهوم مول
مول، در شیمی، واحد علمی استانداردی برای اندازهگیری مقادیر زیاد از اجزای بسیار کوچک مانند اتمها، مولکولها یا سایر ذرات ترکیبات است.
مول پیشتر به عنوان تعداد اتمهایی که بهطور تجربی در ۱۲ گرم کربن-۱۲ یافت میشود تعریف شده بود. تعداد واحدهای موجود در یک مول همچنین به احترام فیزیکدان ایتالیایی آمدئو آووگادرو به نام عدد آووگادریا ثابت آووگادرو نامیده میشود. آووگادرو پیشنهاد داد که حجمهای مساوی از گازها تحت شرایط یکسان، تعداد یکسانی مولکول دارند. این فرضیه در تعیین وزنهای اتمی و مولکولی مفید واقع شد و منجر به پیدایش مفهوم مول در شیمی گردید.

مفهوم مول پارامتری است که برای بیان مقدار ماده استفاده میشود. این موضوع به طور تجربی ثابت شده است که یک اتم گرم از هر عنصر و همچنین یک مولکول گرم از هر ماده، مقدار یکسانی از ذرات را در خود دارد. عدد تعیین شده به طور تجربی برابر با است. پس از کشف مفهوم مول، مشکل یافتن جرمهای اتمی مطلق اتمها حل شد. زیرا مفهوم مول به شمارش تعداد اتمها یا مولکولها در مقدار معین از ماده کمک میکند.
به عنوان مثال، در واکنش شیمیایی دو مول آب به دو مول هیدروژن مولکولی و یک مول اکسیژن مولکولی تجزیه میشود. مول میتواند برای تعیین سادهترین فرمول ترکیب و همچنین محاسبه مقادیر موجود در واکنشهای شیمیایی مورد استفاده قرار گیرد. در هنگام بررسی واکنشهایی که در محلولها رخ میدهند، مفهوم مرتبط با مورلاریته مفید است. مورلاریته (M) به عنوان تعداد مولهای یک حلال در یک لیتر محلول تعریف میشود.
مفهوم جرم مولی
یکی از مفاهیم مهم در معادلات استوکیومتری، مفهوم جرم مولی است. جرم مولی نسبت پرکاربرد بین جرم ذرات و مقدار مول آنهاست. جرم مولی هر ماده مقدار وزن یک مول از آن بر حسب گرم است و برای هر عنصر مقداری منحصر به فرد دارد. این مقادیر برای هر اتم یا یون در جدول تناوبی ارائه شده و در دسترس هستند. برای ترکیبات و مولکولها، جرم مولی مجموع اجرام مولی تمام اتمهاست. در ادامه مثالی برای درک بهتر این موضوع آورده شده است.
برای محاسبه جرم مولی آب روش زیر را بهکار میگیریم.
جرم مولی =
در این معادله، ۱.۰۰۷۹۴ جرم مولی هیدوژن و ۱۵.۹۹۹۴ جرم مولی اکسیژن است.
مفهوم ضریب استوکیومتری
ضرایب استوکیومتری اعدادی هستند که در معادله واکنشهای شیمیایی در سمت چپ عناصر نوشته میشوند و به ما نشان میدهند مواد با چه نسبتی باهم ترکیب شده و فراوردهها را با چه نسبتی تولید میکنند.
ضرایب استوکیومتری یک واکنش موازنه شده، نسبتی همواره ثابت دارند و این نسبت هرگز تغییر نمیکند.
تفسیر واکنشهای شیمیایی
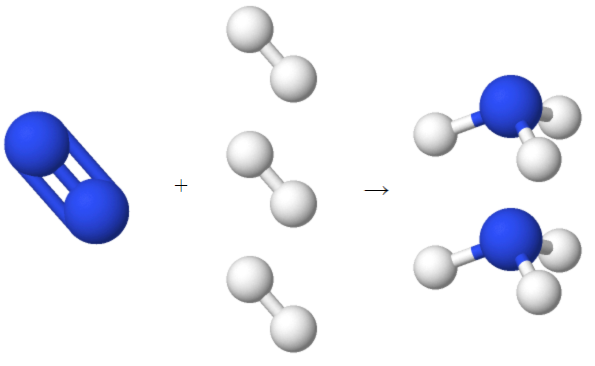
در مبحث قبلی آموختیم که یک مول از هر ماده مقدار عدد آووگادرو ضرب در مقدار ذرات آن ماده است. حال میخواهیم بدانیم این مفهوم را چگونه میتوان در واکنشهای شیمیایی استفاده کرد. برای مثال معادله واکنش تولید آمونیاک را در نظر بگیرید. در این واکنش آمونیاک از هیدروژن و نیتروژن تولید میشود و یک فرایند صنعتی بسیار مهم به نام فرایند هابر است.
ضرایب سمت چپ عناصر، ضرایب استوکیومتری هستند که به ما میگویند چه تعداد از هر ماده در واکنش شرکت میکنند. برای هر واحد گاز نیتروژن، ۳ واحد گاز هیدروژن داریم و از واکنش آنها ۲ واحد گاز آمونیاک به دست میآید. این واحد به کار رفته میتواند مقدار مول، مولکول یا ضرایبی از این مقادیر باشد.
موازنه واکنشهای شیمیایی
با اینکه در طول یک واکنش شیمیایی ترکیبهای شیمیایی تجزیه شده و ترکیبهای جدیدی شکل میگیرند، اتمهای موجود در واکنش دهندهها ناپدید نمیشوند و اتمهای جدیدی برای تشکیل محصولات ظاهر نمیشوند. در واکنشهای شیمیایی، اتمها هرگز خلق یا نابود نمیشوند. همان اتمهایی که در واکنش دهندهها حضور دارند، در محصولات نیز وجود دارند و فقط به ترتیبهای متفاوتی جایگیری کردهاند. در یک معادله شیمیایی، تعداد اتمها باید در دو طرف معادله، یعنی سمت واکنش دهندهها و محصولات، برابر باشد.
اصل تعادل واکنشهای شیمیایی، براساس قانون بقای جرم است که بیان میکند مواد در هر فرمی، مانند اتمها و مولکولها، نمیتوانند خلق یا نابود شوند. این بدان معناست که باید جرم یکسانی از اتمها در هر دو سمت معادله شیمیایی وجود داشته باشد و بنابراین تعداد یکسانی از اتمها نیز باید وجود داشته باشد.
به عنوان مثال، واکنش شیمیایی ساده را در نظر بگیرید. این معادله از پیش موازنه است زیرا تعداد اتمهای Ca و Cl در هر دو سمت یکسان است. موازنه معادله شامل تغییر ضرایب است. ضرایب اعدادی هستند که قبل واکنش دهندهها یا محصولات قرار میگیرند تا آنها را ضرب کنند.
برای مثال معادله واکنش شیمیایی تولید آب را از اتمهای اکسیژن و هیدروژن در نظر بگیرید. اگر یک مول از مولکول اکسیژن و یک مول از مولکول هیدروژن داشته باشیم فرم مولکولی واکنش به شکل زیر در میآید.
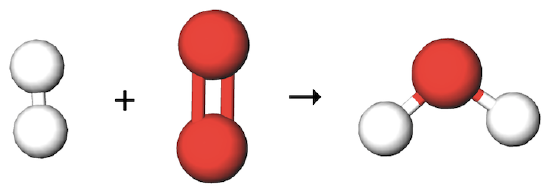
با توجه به معادله و شکل بالا متوجه میشویم که یکی از اتمهای اکسیژن در این معادله استفاده نشده است. درصورتی که طبق قانون پایستگی جرم، هیچ اتمی از بین نرفته و به وجود نمیآید. پس باید در این واکنش هردو اکسیژن استفاده شوند و به ازای آنها دو مولکول آب تولید شود.
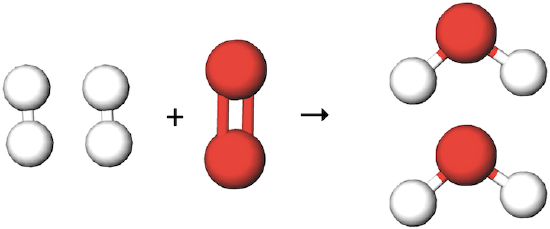
در واکنشهای شیمیایی در کنار و سمت چپ و پایین و سمت راست علامت عناصر عددهایی مشاهده میشوند. زیرنویس عناصر که مربوط به فرمول تجربی و فرم کلی مولکول در طبیعت هستند در سمت راست و پایین علامت عناصر قرار میگیرند.
توجه داشته باشید که ضریب که در سمت چپ یک مولکول قرار میگیرد، با زیرنویس که در اندازه کوچکتر در سمت راست مولکول ظاهر میشود، متفاوت است. ضریب نشاندهنده تعداد مولکولها است. زیرنویس نشاندهنده تعداد اتمهای یک عنصر خاص در هر مولکول است. برای مثال، در ، ضریب ۳ و زیرنویس ۲ است. برای تعیین تعداد کل اتمهای موجود، باید ضریب را در زیرنویس ضرب کرد. تعداد کل اتمها در هر مولکول به معنای کل ۶ اتم O است.
موازنه معادلات شیمیایی هرگز شامل تغییر زیرنویس یک مولکول نیست، بلکه فقط ضریب را تغییر میدهد. تغییر زیرنویس ترکیب شیمیایی مولکول را تغییر میدهد و تعداد مولکولها راتغییر نمیدهد.

چگونه میتوان معادله را موازنه کرد؟
برای موازنه واکنش شیمیایی مراحل زیر باید انجام بگیرند.
- ابتدا، اتمها را در هر سمت شمارش کنید.
- معمولا پیچیدهترین ترکیب ابتدا برای موازنه انتخاب میشود
- ضریب یکی از مواد را تغییر دهید. (معمولا سادهترین ترکیب ابتدا انتخاب میشود.)
- کوچکترین مضرب مشترک بین این دو ماده انتخابی به عنوان ضریب انتخاب میشود.
- یونهای چند اتمی اگر در دو طرف معادله واکنش وجود داشته باشند به شکل یک اتم واحد شمارش میشوند.
- گاهی ممکن است برای موازنه از کسر در ضرایب استفاده شود. در مرحله آخر کل معادله در مخرج کسر ضرب میشود.
- در آخرین مرحله، دوباره تعداد اتمها را شمارش کنید تا معادله موازنه باشد.
به عنوان مثال، واکنش زیر واکنش شیمیایی است که نیاز به موازنه دارد.
گام اول شمارش اتمها در هر سمت است. در سمت چپ، ۲ اتم هیدروژن و ۲ اتم اکسیژن وجود دارد و در سمت راست، ۲ اتم هیدروژن و ۱ اتم اکسیژن. این معادله هنوز موازنه نیست زیرا تعداد اتمهای اکسیژن متفاوت است.
گام دوم تغییر ضریب یکی از مواد با هدف برابر کردن تعداد هر اتم در سمت چپ و راست است. از آنجا که تعداد اتمهای اکسیژن در سمت راست کافی نیست، با افزایش ضریب محصول، ، شروع میکنیم. وقتی ضریبی را انتخاب میکنید، سعی کنید ضریبی به اندازه ممکن کوچک انتخاب کنید. در این مورد، ضریب برابر با ۲ خواهد بود. توجه داشته باشید که تغییر ضریب بر تمام اتمهای موجود در مولکول تاثیر میگذارد. قرار دادن عدد ۲ قبل از تعداد اتمهای هیدروژن و اکسیژن را در ۲ ضرب میکند. علاوه بر این، دقت کنید که تنها یک ضریب را در یک زمان تغییر دهید تا از سردرگمیجلوگیری کنید.
مرحله سوم شمردن اتمها در هر سمت دوباره و بررسی دوباره موازنه است. اکنون که معادله را به تغییر دادهایم، در سمت چپ ۲ اتم هیدروژن و ۲ اتم اکسیژن داریم، اما در سمت راست ۴ اتم هیدروژن و ۲ اتم اکسیژن وجود دارد. اتمهای اکسیژن موازنه شده اند، اما تعداد اتمهای هیدروژن در سمت چپ کم است. اگر ضریب را به ۲ تغییر دهیم، در سمت چپ ۴ اتم هیدروژن و ۲ اتم اکسیژن خواهیم داشت و در سمت راست نیز ۴ اتم هیدروژن و ۲ اتم اکسیژن داریم. معادله موازنه شده است.
در ادامه دومثال دیگر برای درک بهتر موازنه واکنشهای شیمیایی آورده شده است.
مثال ۱
برای تمرین بیشتر معادله واکنش اکسید شدن آلومینیوم را در نظر بگیرید.
پیچیده ترین ترکیب است که در آن دو الومینیوم و سه اکسیژن وجود دارد. در سمت چپ معادله یک آلومینیوم و دو اکسیژن داریم. کوچکترین مضرب مشترک ۲ و ۳ عدد ۶ است پس برای آنکه ۶ اکسیژن در هر سمت داشته باشیم، مولکول اکسیژن ضریب ۳ و آلومینیوم اکسید ضریب ۲ میگیرد.
در نهایت برای موازنه آلومینیوم به اتم آلومینیوم واکنش دهنده ضریب ۲ میدهیم تا در هر دو طرف ۴ اتم آلومینیوم داشته باشیم.
مثال ۲
میخواهیم واکنش سوختن بوتان مایع را موازنه کنیم.
با مشاهده این معادله متوجه میشویم پیچیدهترین ترکیب بوتان است و باید اول موازنه شود. با شمارش تعداد کربنهای دوطرف معادله به کربن دیاکسید ضریب ۴ میدهیم.
سپس برای موازنه تعداد هیدروژنهای معادله به آب ضریب ۵ میدهیم.
درنهایت به موازنه تعداد اکسیژنها میرسیم. در سمت راست معادله بالا ۱۳ اکسیژن و در سمت چپ دو اکسیژن داریم پس اکسیژن سمت چپ باید ضریب ۱۳/۲ بگیرد.
در نهایت برای از بین بردن کسر، کل معادله در ۲ ضرب میشود و معادله موازنه میشود.
درک مفهوم کسرهای تبدیل
کسرهای تبدیل عدد یا فرمولی هستند که برای تبدیل یک اندازه در یک واحد اندازهگیری به همان اندازه در یک مجموعه دیگر از واحدهای اندازهگیری به آنها نیاز داریم. این کسرها معمولا به صورت نسبت یا کسر عددی ارائه میشود که میتوانند به عنوان ضریب ضرب استفاده شود. برای مثال، فرض کنیم طولی داریم که به واحد فوت اندازهگیری شده است و میخواهیم آن را به متر گزارش دهیم. اگر بدانیم که در هر متر ۳.۰۴۸ فوت وجود دارد، میتوانیم از این مقدار به عنوان کسر تبدیل استفاده کنیم تا طول معادل را در واحد متر محاسبه کنیم.
کسر تبدیل از دانش ما درباره روابط بین واحدها استفاده میکند تا بتوانیم واحدی را به واحدی دیگر تبدیل کنیم. به عنوان مثال دیگر، اگر بدانیم که در هر اینچ ۲.۵۴ سانتیمتر وجود دارد (یا ۲.۲ پوند در هر کیلوگرم یا ۱۰۱.۳ کیلوپاسکال در هر اتمسفر)، تبدیل این واحدها به یکدیگر با استفاده از روابط ریاضی ساده امکانپذیر میشود. دانستن برخی تبدیلهای رایج مانند دما، اندازه و فشار اهمیت زیادی دارد.

آسانترین روش برای انجام محاسبات استوکیومتری شامل استفاده از کسرهای تبدیل است. کسر تبدیل نسبت (یا کسری) است که رابطه بین دو واحد مختلف را نشان میدهد. یک کسر تبدیل همواره برابر با ۱ است. یعنی صورت و مخرج آن واحدهای اندازهگیری از یک نوع ( طول، وزن، حجم و ...) و مقادیر کمی آن معادلسازی شدهاند.
برای مثال کسری که صورت آن ۱ لیتر و مخرج آن ۱ متر مکعب، یا کسری که صورت آن ۱۰۰۰ گرم و مخرج آن یک کیلوگرم یا بالعکس باشد.
انواع کسرهای تبدیل استوکیومتری
فرایند تبدیل واحدهای معلوم به مولها از طریق کسرهای تبدیل استوکیومتری انجام میشود. در ادامه، مهمترین و رایجترین کسرهای تبدیل برای تبدیل استوکیومتری بین مول و گرم، مول و حجم گازها، مول و مولکولها، و مول و محلولها را معرفی میکنیم. این کسرهای تبدیل به همان شیوهای که در بخش قبلی بحث شد عمل میکنند. همچنین، توجه داشته باشید که هرچند این کسرهای تبدیل استوکیومتری بر تبدیل از سایر واحدها به مول تمرکز دارند، میتوانند به صورت معکوس هم استفاده شوند و شما را قادر سازند تا مقادیر را از مول به واحد دیگری تبدیل کنید.
در شیمی از چند کسر تبدیل استوکیومتری برای تبدیل واحدها استفاده میشوند که در ادامه توضیح داده خواند شد.
- تبدیل تعداد ذرات تشکیل دهنده ماده و مولها
- تبدیل مول به مول در معادله شیمیایی
- تبدیل گرم به مول و بالعکس در معادله شیمیایی
- تبدیل لیتر به مول و بالعکس در معادله شیمیایی
- تبدیل مول به حجم گاز و بالعکس در معادله شیمیایی
- تبدیل جرم به جرم در معادله شیمیایی
تبدیل تعداد ذرات تشکیل دهنده ماده و مولها
عدد آووگادرو کسر تبدیل استوکیومتری لازم برای تبدیل تعداد ذرات به مولها را فراهم میکند. در هر مول از یک ماده، واحد فرمولی از ذرات وجود دارد. واحد فرمولی به مادهای که در حال بررسی آن هستیم اشاره دارد، چه ترکیب، مولکول، اتم یا یون باشد. واحد فرمولی کوچکترین واحد یک ماده است که همچنان ویژگیهای آن ماده را حفظ میکند و سادهترین راه برای نوشتن فرمول ماده بدون استفاده از ضرایب است. برخی از واحدهای فرمولی رایج که جزو فرمولهای کتاب شیمی یازدهم هستند، در زیر آمدهاند:
- ترکیبات:
- مولکولها:
- اتمها:
- یونها:
از آنجا که ۱ مول = واحد فرمولی است، تبدیل واحد فرمولی به مول به سادگی انجام میشود:
مولها = تعداد واحدهای فرمولی ÷
تبدیل مول به مول در معادله شیمیایی
برای محاسبه تعداد مولهای یک ماده مورد نظر از تعداد مولهای معلوم از هر واکنش دهنده یا محصول، نیاز به یک کسر تبدیل استوکیومتری داریم. مراحل به شرح زیر است:
1. مقدار معلوم و مقدار مورد نظر را بنویسید.
2. معادله شیمیایی موازنه شده را بنویسید.
3.تساوی بین مواد معلوم و مواد مورد نظر را بنویسید.
4. کسر تبدیل استوکیومتری را بنویسید که در آن ماده معلوم در مخرج و ماده مورد نظر در صورت باشد.
5. مقدار معلوم را با کسر تبدیل استوکیومتری ضرب کنید. دوباره بررسی کنید که اطمینان حاصل کنید که ماده معلوم حذف شده و ماده مورد نظر در پاسخ باقی مانده است.
در ادامه دو مثال برای درک بهتر این موضوع آورده شده اند.
مثال ۱
تعداد مولهای گلوکز تولید شده از ۳.۰ مول دیاکسید کربن در واکنش فتوسنتز را محاسبه کنید.
راهحل این مسئله در ادامه آورده شده است.
- معلوم: ۳.۰ مول ، مورد نظر: چند مول
- معادله شیمیایی:
- تساوی مورد نظر:
۶ مول = ۱ مول
- کسر تبدیل استوکیومتری:
- محاسبات:
بنابراین، ۰.۵۰ مول گلوکز تولید میشود.

در ادامه این مطلب از مجله فرادرس مثالی دیگر برای درک بهتر این کسر تبدیل استوکیومتری آورده شده است.
مثال ۲
در معادله واکنش زیر چند مول منیزیم نیاز است تا ۳ مول گاز هیدروژن تولید شود؟
طبق معادله بالا نسبت مولی منیزیم به هیدروژن ۱:۱ است پس خواهیم داشت:
تبدیل گرم به مول و بالعکس در معادله شیمیایی
جرم مولی ترکیب (یا عنصر) به عنوان جرم یک مول از ترکیب تعریف میشود. همانطور که از تعریف برمیآید، این مقدار بر حسب گرم بر مول اندازهگیری میشود و با جمعکردن وزن مولی تمام اتمهای موجود در ترکیب به دست میآید. وزنهای مولی در جدول تناوبی بر حسب amu (واحد جرم اتمی) ارائه میشوند، اما بهطور قراردادی، amu معادل جرم مولی است. به عبارت دیگر، یک مول از یک اتم کربن با وزن 12 amu برابر با 12 گرم خواهد بود.
جرم مولی را میتوان به عنوان یک کسر تبدیل در محاسبات استوکیومتری با استفاده از معادله زیر به کار برد.
مولها = گرم بر گرم جرم مولی ماده
بسیاری از محاسبات شیمیایی به تعداد مولهای یک ماده نیاز دارند، اما چطور میتوان یک مول را اندازه گرفت؟ یکی از روشهای رایج این است که جرم را به گرم اندازهگیری کرده و آن را به مول تبدیل کنیم. تبدیل گرم به مول با چند مرحله ساده قابل انجام است.
برای مثال برای تعیین فرمول مولکولی یک ماده به روش زیر عمل میکنیم.
- با استفاده از جدول تناوبی، جرم اتمیهر عنصر در مولکول را پیدا کنید.
- جرم اتمیهر عنصر را در تعداد اتمهای آن عنصر در مولکول ضرب کنید. این عدد توسط زیرنویس کنار نماد عنصر در فرمول مولکولی نشان داده میشود.
- این مقادیر را برای هر اتم مختلف در مولکول با هم جمع کنید. این مقدار، جرم مولکولی مولکول را به دست میدهد. این عدد برابر با تعداد گرمها در یک مول از آن ماده است.
- تعداد گرمهای ماده را بر جرم مولکولی آن تقسیم کنید.
پاسخ، تعداد مولهای ترکیب خواهد بود.

در ادامه دو مثال برای درک بهتر این موضوع آورده شده اند.
مثال ۱
فرض کنید ۱۸ گرم دارید. مراحل به این صورت خواهد بود:
- فرمول مولکولی:
- جرم اتمیهیدروژن: ۱.۰۱ گرم بر مول، جرم اتمیاکسیژن: ۱۶ گرم بر مول
- محاسبه جرم مولکولی: گرم بر مول
- تعداد مولها:
به این ترتیب، ۱۸ گرم آب معادل ۱ مول آب است.
مثال ۲
میخواهیم میزان AgCl رسوبی تشکیل شده حاصل از واکنش ۲ مول کلسیم کلرید را طبق واکنش زیر به دست آوریم.
میزان جرم مولی نقره کلرید برابر با ۱۴۳.۳ گرم بر مول است و نسبت ضرایب استوکیومتری این دو ماده ۱:۲ است. پس خواهیم داشت:
تبدیل لیتر به مول و بالعکس در معادله شیمیایی
محلولها در مباحث شیمیایی به تفصیل بیشتری مورد بحث قرار میگیرند. اما تبدیل بین اندازهگیریهای محلول و مولها نیز امکانپذیر و نسبتا آسان است. غلظت میتواند بهعنوان یک کسر تبدیل استوکیومتری بین مقدار حلشونده و مقدار محلول یا حلال (بسته به تعریف واحد غلظت) عمل کند. بنابراین، غلظتها میتوانند در انواع مختلف مسائل استوکیومتری مفید باشند. در بسیاری از موارد، بهتر است از تعریف اصلی واحد غلظت استفاده شود. زیرا این تعریف، کسر تبدیل استوکیومتری را فراهم میکند.
مولاریته به عنوان تعداد مولهای حلشونده تقسیم بر تعداد لیترهای حلال تعریف میشود. با تغییر این معادله برای محاسبه تعداد مولها، خواهیم داشت:
مولها = مولاریته × لیترهای محلول
یک مثال ساده از استفاده از واحد غلظت بهعنوان کسر تبدیل استوکیومتری، زمانی است که ما از تعریف واحد غلظت استفاده کرده و آن را بازنویسی میکنیم.
در ادامه دو مثال برای درک بهتر این موضوع آورده شده اند.
مثال ۱
فرض کنید بپرسیم چند مول حلشونده در ۰.۱۰۸ لیتر از محلول ۰.۸۸۷ مولار NaCl وجود دارد. چون ۰.۸۸۷ مولار یعنی ۰.۸۸۷ مول در هر لیتر، میتوانیم از این بیان غلظت بهعنوان کسر تبدیل استفاده کنیم:
مثال ۲
مسائل پیچیدهتر استوکیومتری که از واکنشهای شیمیایی موازنه استفاده میکنند، میتوانند از غلظتها بهعنوان کسرهای تبدیل استفاده کنند. بهعنوان مثال، فرض کنید معادله شیمیایی زیر یک واکنش را نشان میدهد:
اگر بخواهیم بدانیم چه حجمی از محلول ۰.۵۵۵مولار برای واکنش با ۱.۲۵ مول نیاز است، ابتدا از معادله شیمیایی موازنه برای تعیین تعداد مولهای که واکنش میدهند استفاده میکنیم و سپس با استفاده از غلظت، آن را به لیتر محلول تبدیل میکنیم:
این روش را میتوان گسترش داد و به جای شروع از تعداد مولهای یک واکنش دهنده، از جرم یک واکنش دهنده استفاده کرد. برای مطالعه و یادگیری بیشتر درباره غلظت محلولها و واحدهای اندازهگیری آنها، پیشنهاد میکنیم مطلب زیر از مجله فرادرس را مطالعه بفرمایید.
تبدیل مول به حجم گاز و بالعکس در معادله شیمیایی
کپسولهای گاز کوچک اغلب برای تامین گازها در واکنشهای شیمیایی استفاده میشوند. دانستن نحوه محاسبه پارامترهای لازم برای گازها بسیار مفید است تا از تمام شدن زودتر از حد انتظار گاز در این واکنشها جلوگیری شود.
حجم مولی در شرایط استاندارد (STP)
حجم مولی در شرایط استاندارد (STP) میتواند برای تبدیل بین مولها و حجم گاز استفاده شود. در شرایط استاندارد دما و فشار (STP)، ۱ مول گاز برابر با ۲۲.۴ لیتر حجم دارد. این تساوی مبنای کسر تبدیل استوکیومتری تبدیل مول به حجم گاز است.
- تبدیل از مولها به حجم گاز:
برای تبدیل تعداد مولها به حجم گاز، از کسر تبدیل استوکیومتری زیر استفاده کنید:
با استفاده از این کسرها، میتوانید به راحتی محاسبات مربوط به گازها را انجام دهید و مطمئن شوید که مقدار گاز برای واکنشهای شیمیایی کافی است.
تبدیل جرم به جرم در معادله شیمیایی
معادله شیمیایی یک کسر تبدیل مول به مول را ارائه میدهد. اگر ماده معلوم بر حسب گرم و ماده مورد نظر نیز بر حسب گرم باشد، دو کسر تبدیل اضافی بر اساس جرم مولی نیاز است. به عبارت دیگر، تبدیلهای زیر مورد نیاز است:
جرم ماده معلوم ⇒ مول ماده معلوم ⇒ مول ماده مورد نظر ⇒ گرم ماده مورد نظر
جرم مولی معکوس ماده معلوم، اولین کسر تبدیل است. کسر تبدیل مول به مول از معادله شیمیایی دومین کسر تبدیل است، و جرم مولی ماده مورد نظر سومین کسر تبدیل مورد نیاز است. اطمینان حاصل کنید که هر کسر تبدیل، واحد مخرج ضریب سمت راست خود را حذف میکند و واحد مورد نظر در پاسخ باقی میماند. مثالهای زیر این محاسبات را توضیح میدهند.
مثال ۱
چه مقدار گرم Mg برای تولید 1.01 گرم گاز H2 در این واکنش نیاز است:
راه حل این مسئله به روش زیر انجام میشود.
جرم داده شده: 1.01 گرم H2، جرم مورد نیاز: چند گرم Mg؟
جرم مولی H2 = 2 × 1.008 = 2.016 گرم بر مول H2
جرم مولی Mg = 24.305 گرم بر مول.
تساویهای مورد نیاز:
1 مول Mg = 1 مول H2
1 مول H2 = 2.016 گرم H2
1 مول Mg = 24.305 گرم Mg.
برای محاسبه با ضرب مقدار داده شده به ترتیب با سه کسر تبدیل استوکیومتری مورد نیاز از تساویها معادله زیر را خواهیم داشت.
پاسخ: 11.9 گرم Mg نیاز است.
مثال ۲
چند گرم گلوکز از مصرف ۲۲ گرم کربن دی اکسید در فرایند فوتوسنتز به دست میآید؟
در معادله شیمیایی فوتوسنتز داریم:
ابتدا جرم مولی کربن دی اکسید و گلوکز را به دست میاوریم.
نسبت ضرایب استوکیومتری کربن دی اکسید و گلوکز در فوتوسنتز به شکل ۶:۱ است. پس خواهیم داشت:
جدول راهنمای کسرهای تبدیل استوکیومتری
کار با مولها همیشه چالشبرانگیز است و در کلاس شیمی عمومی معمولا مجبور هستید تعداد زیادی تبدیل مربوط به مولها را انجام دهید. چه بخواهید از مول به گرم، مول به حجم، یا مول به ذرات (اتمها یا مولکولها) تبدیل کنید، جدول راهنمای زیر به شما یادآوری میکند که چگونه هر نوع تبدیل را انجام دهید.
| نوع تبدیل | روش تبدیل |
| تبدیل مول به مول | از ضرایب معادله شیمیایی موازنه برای تعیین کسر تبدیل استوکیومتری استفاده کنید. مطمئن شوید که واحدها بهدرستی حذف میشوند تا مقدار مول صحیح به دست آید. |
| تبدیل مول به ذرات (اتمها، مولکولها، یا واحدهای فرمولی) | مقدار مول را در عدد آووگادرو، ضرب کنید. |
| تبدیل ذرات (اتمها، مولکولها، یا واحدهای فرمولی) به مول | تعداد ذرات را بر عدد آووگادرو، تقسیم کنید. |
| تبدیل مول به جرم (گرم) | مقدار مول اولیه را در جرم مولی ترکیب که از جدول تناوبی تعیین شده است، ضرب کنید. |
| تبدیل جرم (گرم) به مول | جرم اولیه را بر جرم مولی ترکیب که از جدول تناوبی تعیین شده است، تقسیم کنید. |
| تبدیل مول به حجم (لیتر) | مقدار مول را در مقدار ثابت حجم مولی، 22.4 لیتر ضرب کنید. |
| تبدیل حجم (لیتر) به مول | حجم اولیه را بر مقدار ثابت حجم مولی، 22.4 لیتر تقسیم کنید. |
تفاوت ضرایب و کسرهای تبدیل استوکیومتری
در یک واکنش موازنه شده، هردو سمت معادله واکنش، یک تعداد اتم دارند. ضرایب استوکیومتری اعدادی هستند که قبل از هر عنصر، یون یا مولکول نوشته میشوند تا تعداد عناصر را در دو سمت معادله واکنش برابر کنند. کسرهای تبدیل استوکیومتری، میتوانند از نظر عددی کسر یا عدد کامل باشند و برای تبدیل واحدها و بهدست آوردن مقادیر کمی یک ماده در معادله واکنش به کار میروند.
برای مثال معادله زیر را در نظر بگیرید.
با مشاهده معادله بالا و توجه به ضرایب استوکیومتری میتوان دریافت که ۲ مول از ماده اسید کلریدریک با دو مول سدیم واکنش داده و دو مول سدیم کلرید و یک مول گاز هیدروژن تولید میشود. این نسبت ضرایب (۲:۲:۲:۱) همواره ثابت است و تغییر نمیکند. به این ضرایب، ضرایب استوکیومتری گفته میشود.
واکنش دهنده محدودکننده و بازده نظری واکنش
در واکنش شیمیایی، ممکن است یکی از واکنش دهندهها مقدار محصولات تولیدی را محدود کند. زمانی که این اتفاق میافتد، به آن واکنش دهنده، واکنش دهنده محدودکننده گفته میشود. مقدار محصولی که هنگام مصرف کامل واکنش دهنده محدودکننده در واکنش تشکیل میشود و معمولا با محاسبات استوکیومتری به دست میآید، به عنوان بازده نظری شناخته میشود.
به عنوان مثال، فرض کنید میخواهیدهاتداگ درست کنید. اگر تعداد نانهایهاتداگ کمتر از تعداد سوسیسها باشد، تعداد نانها تعیین میکند که چندهاتداگ کامل میتوانید درست کنید. در اینجا، نانها به عنوان واکنش دهنده محدودکننده عمل میکنند و بازده نظری شما چهارهاتداگ کامل خواهد بود (بر اساس تعداد نانهای موجود).
برای درک بهتر واکنش دهنده محدودکننده و بازده نظری واکنش مثالی در ادامه آورده شده است.

یک نمونه ۲.۸ گرمی از آلومینیوم با یک نمونه ۴.۱۵ گرمی از کلرین طبق معادله زیر واکنش میدهد:
بازده نظری در این واکنش چیست؟
برای حل این مسئله، ابتدا باید تعیین کنیم که کدام واکنش دهنده، Al یا کلر، محدودکننده است. برای این کار، میتوانیم جرمهای هر دو واکنش دهنده را به مول تبدیل کرده و سپس با استفاده از نسبتهای مولی از معادله موازنه، واکنش دهنده محدودکننده را شناسایی کنیم. پس از آن، میتوانیم از مقدار واکنش دهنده محدودکننده برای محاسبه بازده نظری استفاده کنیم.
ما با مقایسه نسبت مولی بین Al و Cl2 در معادله موازنه با نسبت مولی واقعی موجود، واکنش دهنده محدودکننده را تعیین خواهیم کرد. در این مورد، نسبت مولی مورد نیاز Al و Cl2 طبق معادله موازنه به شرح زیر است:
2 : 3
این نسبت نشان میدهد که برای هر ۲ مول آلومینیوم ۳ مول کلر نیاز است.
و نسبت مولی واقعی به صورت زیر است:
از آنجایی که نسبت واقعی بزرگتر از نسبت مورد نیاز است، ما بیشتر از مقدار مورد نیاز Al داریم تا به طور کامل با واکنش دهد. این به این معنی است که باید واکنش دهنده محدودکننده باشد. اگر نسبت واقعی کمتر از نسبت مورد نیاز بود، در این صورت به میزان اضافی وجود داشت و Al محدودکننده میبود.
سپس برای محاسبهی بازده نظری این واکنش به روش زیر عمل میکنیم. دقت کنید بازده نظری مقدار محصولی است که زمانی تولید میشود که واکنش دهنده محدودکننده به طور کامل مصرف شود. در این مورد، واکنش دهنده محدودکننده است، بنابراین حداکثر مقدار که میتواند تولید شود به صورت زیر است:
بهدست آوردن فرمول تجربی مواد
یکی از کاربردهای کسرهای تبدیل استوکیومتری، بهدست آوردن فرمول تجربی مواد است. فرمول تجربی مواد مشخص میکند که چه تعدادی از هر اتم در مولکول وجود دارد. این فرمول به وسیله مقایسه تعداد مول موجود از هر اتم در دوطرف واکنش به دست میآید. برای درک بهتر این موضوع، مثالی در ادامه آورده شده است.

- ۱.۰۰۰ گرم از یک مولکول آلی در حضور اکسیژن اضافی میسوزد. فراورده این واکنش ۰.۰۳۳۳ مول کربن دی اکسید و ۰.۵۹۹ گرم آب است. فرمول تجربی این مولکول را بهدست آورید.
برای حل این مسئله باید بدانیم که مولکولهای آلی ترکیبی از اتمهای کربن،هیدروژن و اکسیژن هستند. با نوشتن معادله سوختن این واکنش سعی میکنیم فرمول تجربی را از روی تعداد مولهای موجود فراوردهها پیدا کنیم.
طبق این معادله که بر اساس صورت سوال نوشته شده است، تعداد مولهای کربن و هیدروژن در مولکولهای کربن دی اکسید و آب باید از ماده آلی مورد نظر به دست آمده باشند. همچنین تعداد مولهای اکسیژن نیز جمع مول اکسیژن کربن دی اکسید و آب منهای مول اکسیژن واکنش دهنده به دست میآید.
بنابراین طبق معادلات زیر تعداد مول هریک از عناصر به دست میآید.
مول اکسیژن در کربن دی اکسید و آب نیز به روش زیر به دست میایند.
با توجه به قانون بقای جرم، میتوانیم از تفاوت مقدار مول هریک از عناصر در دوطرف واکنش، مقدار مول این عناصر را در ماده مجهول به دست آوریم.
با تفریق مقدار مول اتمهای کربن، هیدروژن و اکسیژن ترکیبات معلوم از مقدار کلی این مقادیر برای ماده مجهول به دست میآیند.
پس ماده ما است.
بهدست آوردن فرمول مولکولی از روی فرمول تجربی
فرمول مولکولی مواد همان فرمول تجربی است که در ضریبی ضرب شده است. درواقع فرمول تجربی، سادهترین واحد یک مولکول است. اگر مقدار جرم فرمول تجربی مادهای را به دست آوریم، با تقسیم وزن فرمول مولکولی بر وزن فرمول تجربی، آن ضریب بهدست میآید. بدین ترتیب مشخص میشود چه تعداد از هر گروه از اتمها در فرمول مولکولی ماده وجود دارد.
برای مثال به سوال زیر توجه کنید.
یک ترکیب با فرمول تجربی CH دارای وزن مولکولی ۷۸ گرم بر مول است. فرمول مولکولی این ترکیب را بیابید.
با بهدست آوردن وزن مولی CH و تقسیم وزن مولکولی بر آن، مقادیر به دست میآید.
وزن مولی CH = ۱۳ گرم بر مول
۶ = ۱۳ / ۷۸
پس فرمول مولکولی ۶ عدد از هر کدام از این اتم ها دارد. این ماده بنزن نام دارد و فرمول مولکولی آن است.
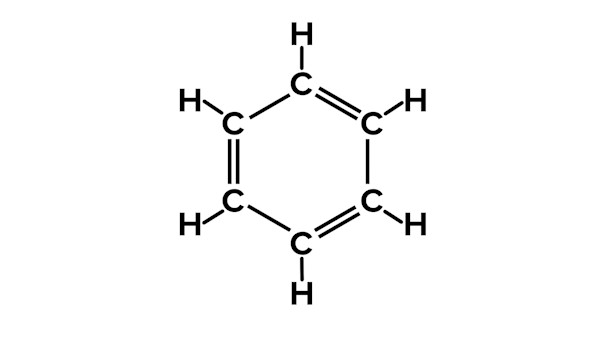
بدین ترتیب با بهدست آوردن نسبت تبدیل بین پارامترهای مختلف و نوشتن کسرهای تبدیل استوکیومتری آنها، میتوان مقادیر مختلف کمی را در معادلات شیمیایی بهدست آورد. این مطالب بهطور کامل در این مقاله از مجله فرادس توضیح داده شد.