پلاریزاسیون – به زبان ساده
در آموزشهای قبلی مجله فرادرس درباره میدانهای الکترومغناطیسی صحبت کردیم. در این آموزش قصد داریم پلاریزاسیون یا قطبش در امواج را بررسی کنیم. پلاریزاسیون یا «پلاریزاسیون موج» (Wave Polarization)، یک خاصیت از «امواج عرضی» (Transverse Waves) است. به طور خلاصه، پلاریزاسیون جهت هندسی نوسانها را مشخص میکند.
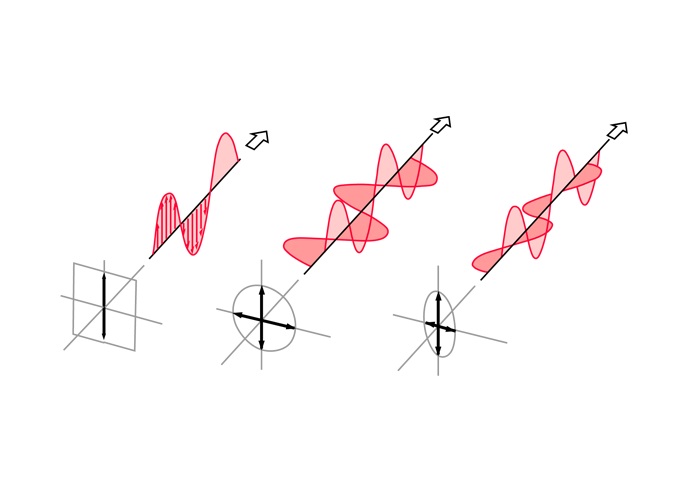
بر اساس تعریف استاندارد انجمن مؤسسه مهندسان برق و الکترونیک (IEEE) برای آنتنها، پلاریزاسیون یک موج تشعشع یافته، به صورت زیر تعریف میشود:
خاصیتی از یک موج الکترومغناطیسی تشعشع یافته که جهت و اندازه نسبی بردار میدان الکتریکی متغیر با زمان را نشان میدهد. به عبارت دیگر اگر بردار میدان الکتریکی را در یک نقطه فضایی ثابت نگه داریم و در جهت انتشار موج به آن نگاه کنیم، منحنی به دست آمده از انتهای بردار نسبت به زمان، به صورت پلاریزاسیون تعریف میشود.
شکل زیر، چرخش یک موج الکترومغناطیسی و منحنی پلاریزاسیون به دست آمده از این میدان را نشان میدهد:
در یک موج عرضی، جهت نوسانها بر جهت حرکت موج عمود است. یک مثال ساده از موج عرضی پلاریزه، ارتعاشات پیشرونده در یک رشته ریسمان است. این رشته میتواند سیم گیتار باشد. شکل زیر، تبدیل پلاریزاسیون دایروی به پلاریزاسیون خطی در یک رشته نخ را نشان میدهد:

بسته به اینکه چگونه رشته را بکشیم، ارتعاشات میتواند در جهت عمودی، افقی یا هر جهتی عمود بر محور رشته باشد. در مقابل، انتشار امواج صوتی در مایع یا گاز را در نظر بگیرید. جابجایی ذرات در ارتعاشات این امواج، همیشه با جهت انتشار موج همجهت خواهد بود. به این امواج، «امواج طولی» (Longitudinal Waves) میگویند. بنابراین در امواج طولی، پلاریزاسیون تعریف نمیشود، چرا که نوسانها همواره همجهت با انتشار موج هستند. از انواع امواج عرضی که پلاریزاسیون دارند، میتوان «امواج الکترومغناطیسی» (Electromagnetic Waves) و «امواج صوتی عرضی» (Transverse Sound Waves) را نام برد. نور، امواج رادیویی و امواج گرانشی از جمله امواج الکترومغناطیسی محسوب میشوند. «امواج برشی» (Shear Waves) نیز از جمله امواج صوتی عرضی هستند. در برخی از انواع امواج عرضی، جابجایی موج فقط به یک جهت محدود میشود. بنابراین این نوع امواج عرضی، پلاریزاسیون ندارند. برای مثال، امواج سطحی در مایعات یا «امواج ثقلی» (Gravity Waves) پلاریزاسیون ندارند. در این امواج، جابجای موج ذرهها همواره در یک صفحه عمودی خواهد بود.
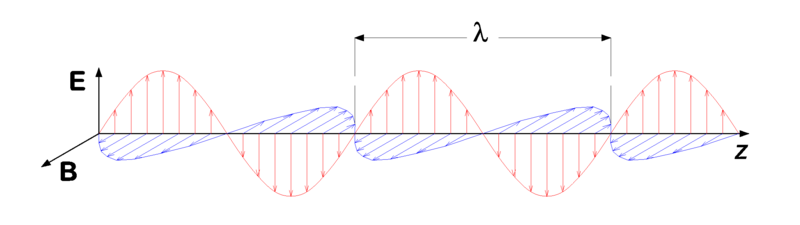
یک موج الکترومغناطیسی مانند نور، از یک میدان الکتریکی و یک میدان مغناطیسی نوسان تشکیل شده است. بین این دو میدان پیوندی وجود دارد و تغییر در یکی، باعث تغییر در دیگری میشود. همچنین این دو میدان، همواره به یکدیگر عمود هستند. این دو میدان همواره بر جهت انتشار موج عمود هستند.
طبق تعریف، میدان الکتریکی، پلاریزاسیون یا قطبش امواج الکترومغناطیسی را تعیین میکند. در «پلاریزاسیون خطی» (Linear Polarization)، میدانها فقط در یک جهت نوسان میکنند. در «پلاریزاسیون دایروی» (Circular Polarization) یا «بیضوی» (Elliptical)، میدانها همزمان با حرکت موج با سرعتی ثابت در یک صفحه میچرخند. این چرخش میتواند دو جهت داشته باشد، اگر میدانها نسبت به جهت حرکت موج، مانند قانون دست راست چرخش کنند، به آن «پلاریزاسیون دایروی راستگرد» (Right Circular Polarization) گویند. به صورت معکوس، اگر میدانها نسبت به جهت حرکت موج در جهت دست چپ حرکت کنند، به آن «پلاریزاسیون دایروی چپگرد» (Left Circular Polarization) گفته میشود.
انتشار نور یا هر موج الکترومغناطیسی دیگر از قطار امواج کوتاه تشکیل شده میشود. خورشید، شعله آتش و یا لامپهای مهتابی از جمله منابع نور هستند. این قطار امواج، ترکیبی از هر دو پلاریزاسیون را در بر دارد. در این حالت، نور را غیر پلاریزه گویند. با عبور نور غیر پلاریزه از یک «پلارایزر» (Polarizer)، نور پلاریزه حاصل میشود. پلارایزر، فقط اجازه عبور یک نوع از نور را میدهد. بیشتر مواد اپتیکی (مانند شیشه)، ایزوتروپیک هستند و پلاریزاسیون نور عبور کرده از آنها تغییر نمیکند. هرچند بعضی مواد، مانند آنهایی که از خود «شکست مضاعف» (Birefringence)، «دو رنگی» (Dichroism) و یا «فعالیت نوری» (Optical Activity) نشان میدهند، میتوانند پلاریزاسیون نور را تغییر دهند. میتوان از این مواد در ساخت «فیلترهای پلاریزه کننده» (Polarizing Filters) استفاده کرد. هنگامی که نور از یک سطح منعکس میشود، بخشی از آن پلاریزه میشود.
پلاریزاسیون، پارامتر مهمی در حوزههای مختلف علوم است. این پارامتر به امواج عرضی مانند اپتیک، لرزهنگاری، امواج رادیویی و مایکروویو مربوط میشود. لیزر، مخابرات راه دور با استفاده از فیبر نوری و یا بیسیم و همچنین رادار، از جمله فناوریهایی هستند که به صورت ویژه از این پارامتر تاثیر گرفتهاند.
مقدمه
بیشتر منابع نوری به صورت منابع «غیر همدوس» (Incoherent) یا «غیر پلاریزه» (Unpolarized) طبقهبندی میشوند. این منابع، شامل ترکیبی تصادفی از امواج هستند که مشخصات فضایی، فرکانس (طول موج)، فاز و حالتهای پلاریزاسیون متفاوتی دارند. هرچند، برای درک امواج الکترومغناطیسی و به خصوص پلاریزاسیون، فقط کافی است که امواج سطحی «همدوس» (Coherent) را در نظر بگیرید. این امواج سینوسی جهت (بردار موج)، فرکانس، فاز و حالت پلاریزاسیون خاص خود را دارند. از آنجا که موج با هر ساختار فضایی را میتوان به ترکیبی از امواج سطحی یا طیف زاویهای آن تجزیه کرد، توصیف یک سیستم اپتیکی مربوط با پارامترهای موج مسطح، امکانپذیر خواهد بود. در این حالت، میتوان پاسخ سیستم را در حالت کلیتر پیشبینی کرد. حالتهای غیرهمدوس را میتوان توسط ترکیب آماری وزندار از امواج غیرهمدوس به هم با توزیعهای فرکانس (طیف آن)، فاز و پلاریزاسیون مشخص مدل کرد.
امواج الکترومغناطیسی عرضی
امواج الکترومغناطیسی (مانند نور)، که در فضای آزاد یا یک محیط ایزوتروپیک همگن غیر تضعیف کننده دیگر حرکت میکنند، به وسیله امواج عرضی قابل توضیح هستند. به این معنی که جهت بردار میدان الکتریکی E و میدان مغناطیسی H عمود بر انتشار موج است. همچنین E و H بر یکدیگر نیز عمود هستند. طبق تعریف، جهت پلاریزاسیون برای یک موج الکترومغناطیسی به وسیله بردار میدان الکتریکی آن داده میشود. فرض کنید یک موج مسطح «تکفام» (Monochromatic) با فرکانس نوری داریم که در جهت منتشر میشود. از آنجا که با یک موج عرضی سروکار داریم، بنابراین میدانهای الکتریکی و مغناطیسی E و H، تنها مولفههایی در جهات و خواهد داشت. بنابراین در این حالت:
با استفاده از نشانهگذاری مختلط یا فازوری، میدانهای الکتریکی و مغناطیسی فیزیکی لحظهای به صورت جزء حقیقی کمیتهای مختلط داده میشوند. این میدانها به صورت تابعی از زمان t و مکان فضایی z داده میشوند. از آنجا که برای یک موج مسطح در جهت میدانها به جهتهای و وابستگی ندارند، این میدانهای مختلط را میتوان به صورت زیر نوشت:
و
طول موج در این محیط برابر است با:
در این رابطه ضریب انعکاس برابر و دوره تناوب موج است. در اینجا، و و و اعداد مختلط هستند. در فرم فشردهتر دیگر از «عدد موج» (wavenumber) و «فرکانس زاویهای» (Angular Frequency) یا فرکانس رادیان استفاده میشود. این دو پارامتر به صورت زیر تعریف میشوند:
در یک فرمولبندی کلی که انتشار به جهت محدود نیست، وابستگی فضایی با عبارت جایگزین میشود. در این حالت را بردار موج مینامند که دامنه آن عدد موج است.
بنابراین میدانهای الکتریکی و مغناطیسی هر کدام دو مولفه غیر صفر مختلط دارند که دامنه و فاز موج در پلاریزاسیونهای و را نشان میدهد. همانطور که گفتیم، برای یک میدان عرضی در جهت ، میدان در جهت پلاریزاسیون ندارد؛ زیرا مولفهای در این جهت ندارد. برای یک محیط با امپدانس مشخصه ، میدانهای مغناطیسی و الکتریکی با رابطه زیر به یکدیگر مرتبط هستند:
و
در یک دیالکتریک، مقداری حقیقی دارد و برابر است با:
در این رابطه، ضریب انعکاس و امپدانس فضای آزاد است. برای یک محیط هادی، امپدانس مختلط است. طبق روابط بالا، حاصلضرب داخلی دو بردار میدان الکتریکی و مغناطیسی ( و ) باید برابر صفر باشد. این مسئله در زیر نشان داده شده است:
رابطه بالا، نشاندهنده متعامد بودن دو بردار است که قابل انتظار نیز هست. پس با دانستن جهت انتشار (در این حالت ) و میتوان موج را به طور مناسب بر حسب میدانهای الکتریکی و توضیح داد. بردار شامل و که برای یک موج عرضی مولفه ندارد، به نام «بردار جونز» (Jones vector) شناخته میشود. بردار جونز در حالت کلی، علاوه بر تعیین حالت پلاریزاسیون موج دامنه و فاز موج را نیز مشخص میکند. به طور خاص، شدت موج نور با جمع مربعات دامنه مولفههای میدان الکتریکی متناسب است. شدت موج نور برابر است با:
هرچند، حالت پلاریزاسیون فقط به نسبت مختلط به وابسته است. حال موجی با مولفههای و را در نظر بگیرید. در این موج رابطه زیر برقرار است:
این حالت، مربوط به یک موج با شدت توان وات بر متر مربع در فضای آزاد () است. از آنجا که فاز مطلق موج در حالت پلاریزاسیون آن بی تاثیر است، به صورت قراردادی فرض میکنیم که فاز برابر صفر است. به عبارت دیگر، عددی حقیقی و مختلط است. در این شرایط، و را میتوان به صورت زیر نوشت:
\begin{align}
&e_x = \sqrt{\frac{1+Q}{2}}\\
&e_y = \sqrt{\frac{1-Q}{2}}e^{i\phi}
\end{align}
در روابط بالا، حالت پلاریزاسیون به وسیله مقدار و فاز نسبی تعیین میشود. در این حالت مقداری بین و دارد.
امواج غیرعرضی
علاوه بر امواج عرضی، امواجی وجود دارند که در آنها، نوسانها محدود به عمود بر جهت انتشار نیست. از جمله این امواج، میتوان امواج الکترومغناطیسی داخل محیطهای حجیم را نام برد.
در ادامه فرض میشود منظور از امواج، تنها امواج الکترومغناطیسی است و این امواج سطحی در محیط همگن ایزوتروپیک غیر تضعیفکننده منتشر میشوند. در محیطهای غیر ایزوتروپیک (مثل کریستالهای دو شکستی یا انکسار مضاعف) میدانهای الکتریکی و مغناطیسی میتوانند علاوه بر مولفههای عرضی، مولفههای طولی نیز داشته باشند. در این حالت، جابجایی الکتریکی و چگالی شار مغناطیسی همچنان از هندسه بالا تبعیت میکنند. اما به دلیل غیر ایزوتروپیک بودن حساسیت الکتریکی (یا نفوذپذیری مغناطیسی) که در این حالت به وسیله یک تانسور مشخص میشود، جهت E (یا H) ممکن است با جهت D (یا B) متفاوت باشد. حتی در محیط ایزوتروپیک، امواج غیرهمگن میتوانند به محیطی اعمال شوند که ضریب انعکاس آن قسمت موهومی بزرگی دارد. از جمله این محیطها میتوان به رساناهای فلزی اشارده کرد. این میدانها نیز دقیقا عرضی نیستند. امواج سطحی یا امواجی که در موجبر (مثل فیبر نوری) منتشر میشوند، به طور کلی عرضی نیستند. اما میتوان آنها را به صورت مودهای عرضی الکتریکی یا مغناطیسی یا مودهای هایبرید در نظر گرفت.
حتی در فضای آزاد، مولفههای طولی میدان را میتوان در نواحی کانونی تولید کرد. در این نواحی، تقریب سطحی بودن موج از بین میرود. به عنوان یک مثال میتوان نور پلاریزه شده مماسی یا شعاعی را نام برد. در این حالت، میدانهای الکتریکی و مغناطیسی به طور کامل طولی هستند.
برای امواج طولی (مانند امواج صوتی در سیالات)، جهت نوسان به وسیله جهت حرکت موج تعریف میشود. بنابراین در این امواج حتی اشارهای به پلاریزاسیون نیز نمیشود. از سوی دیگر، امواج صوتی در یک جسم حجیم علاوه بر طولی میتوانند عرضی هم باشند. بنابراین در این حالت، میدان سه پلاریزاسیون خواهد داشت.
حالت پلاریزاسیون
پلاریزاسیون، به وسیله حالتهای مختلف پلاریزاسیون و یک موج همدوس سینوسی در فرکانس نوری قابل درک است. بردار نشان داده شده در شکل زیر، نویان میدان الکتریکی توسط یک لیزر تک مود را نشان میدهد. نوسانهای میدان در صفحه xy و انتشار موج در جهت z و عمود بر صفحه میدان است. شکل زیر، بردار میدان الکتریکی را در یک چرخه کامل برای پلاریزاسیون خطی در دو جهت مختلف نشان میدهد. هر کدام از این جهتها، یک حالت پلاریزاسیون مشخص دارند. لازم به ذکر است که پلاریزاسیون خطی در ۴۵ درجه را میتوان به صورت جمع یک موج خطی پلاریزه به صورتی افقی و یک موج خطی پلاریزه به صورت عمودی با دامنه و فاز یکسان دید.
حال اگر بین این دو مولفه پلاریزاسیون افقی و عمودی یک جابجایی فاز داشته باشیم، به «پلاریزاسیون بیضوی» (Elliptical Polarization) میرسیم. هنگامی که جابجایی فاز دقیقا برابر با است، «پلاریزاسیون دایروی» (Circular Polarization) به دست میآید. بنابراین برای تولید پلاریزاسیون دایروی در عمل، لازم است نور پلاریزه شده به صورت خطی را به یک «صفحه یک چهارم طول موج» (Quarter-Wave Plate) اعمال کنیم. به این ترتیب، جابجایی فاز لازم برای ایجاد پلاریزاسیون دایروی ایجاد میشود. در نتیجه جابجایی فاز در این دو مولفه، یک بردار میدان الکتریکی چرخان به دست میآید. شکل زیر، این موج را نشان میدهد:
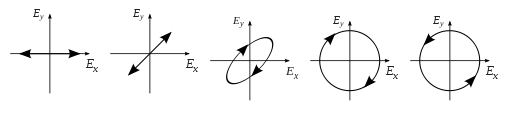
لازم به ذکر است که پلاریزاسیون دایروی یا بیضوی میتواند چرخش میدانی در جهت عقربههای ساعت یا در خلاف جهت عقربههای ساعت داشته باشد. این مسئله به حالتهای پلاریزاسیون مشخص منجر میشود.
البته جهت مولفههای x و y استفاده شده در این آموزش، اختیاری است. انتخاب این سیستم مختصاتی و مشاهده بیضی پلاریزاسیون بر حسب مولفههای پلاریزاسیونهای x و y، به تعریف بردار جونز بر حسب «پلاریزاسیونهای پایه» (Basis Polarization) مربوط است. برای هر مسئله باید از محورهای عمود بر هم مطابق با آن استفاده کرد. برای مثال، محور x میتواند در صفحه موج برخوردی باشد.
همچنین میتوان از جفت توابع پایه متعامد متفاوت برای تعریف حالتهای مختلف پلاریزاسیون و نه فقط پلاریزاسیون خطی استفاده کرد.
برای مثال، انتخاب پلاریزاسیونهای دایروی چپ و راست به عنوان توابع پایه، حل مسائل مربوط به دو شکستی یا دورنگی دایروی را آسان میکند.
پلاریزاسیون خطی
یک موج مسطح هارمونیک را در نظر بگیرید. میدان الکتریکی، مولفههای x و y دارد و در جهت منتشر میشود. این مسئله در شکل زیر نشان داده شده است.
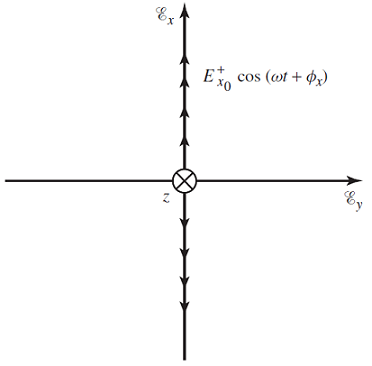
مقادیر لحظهای میدان الکتریکی و مغناطیسی برای این موج، به صورت زیر داده میشود:
و
\begin{aligned}
H & = \hat{a}_y H_y + \hat{a}_x H_x = \textbf{Re}\left[ \hat{a}_y \frac{E_x^+}{\eta} e^{j(\omega t - \beta z)} - \hat{a}_x \frac{E_y^+}{\eta} e^{j(\omega t - \beta z)} \right] \\
&= \hat{a}_y \frac{E_{x0}^+}{\eta} \cos(\omega t - \beta z + \phi_x) - \hat{a}_x \frac{E_{y0}^+}{\eta} \cos(\omega t - \beta z + \phi_y)
\end{aligned}
در این روابط، و مختلط و و حقیقی هستند.
حال به بررسی تغییرات لحظهای بردار میدان الکتریکی در صفحه میپردازیم. برای مثال فرض کنید:
بنابراین، داریم:
مکان هندسی میدان الکتریکی لحظهای به صورت زیر داده میشود:
که یک خط راست است و در همه زمانها در جهت محور جهتگیری میکند. این مکان هندسی، در شکل زیر نشان داده شده است. میدان، پلاریزاسیون خطی در جهت محور دارد.

بنابراین میتوان گفت که اگر بردار یک میدان الکتریکی در یک نقطه از فضا در جهت یک خط مستقیم در هر لحظه از زمان جهتگیری کند، میدان «هارمونیک زمانی» (Time Harmonic) در آن نقطه از فضا پلاریزاسیون خطی دارد. اگر بردار میدان الکتریکی به یکی از دو صورت زیر باشد، گفته میشود که پلاریزاسیون خطی دارد:
- فقط یک مولفه داشته باشد.
- دو مولفه متعامد با پلاریزاسیون خطی داشته باشد، که همفاز هستند یا اختلاف فاز آنها مضرب صحیحی از است.
پلاریزاسیون دایروی
یک موج، پلاریزاسیون خطی دارد اگر حرکت بردار میدان الکتریکی یک رد با مکان هندسی دایروی در فضا ایجاد کند. در لحظات مختلف زمان، شدت میدان الکتریکی این موج دامنه یکسان دارد. جهتگیری فضایی این موج با تغییر بردار میدان الکتریکی به گونهای است که یک مکان هندسی دایروی ایجاد میکند.
پلاریزاسیون دایروی راستگرد (در جهت حرکت عقربههای ساعت)
اگر بردار میدان الکتریکی نسبت به ناظری که روی محور انتشار موج قرار گرفته است در جهت حرکت عقربههای ساعت نوسان کند، گفته میشود که موج، پلاریزاسیون دایروی راستگرد دارد. با رسم مقدار لحظهای بردار میدان الکتریکی در صفحه در همه زمانها، میتوان به پلاریزاسیون موج رسید. مقادیر زیر را در نظر بگیرید:
بنابراین:
مکان هندسی دامنه بردار میدان الکتریکی به صورت زیر داده میشود:
این میدان نسبت به محور ، به اندازه زاویه دارد. این زاویه به صورت زیر محاسبه میشود:
اگر مکان هندسی بردار میدان الکتریکی را در لحظات مختلف در صفحه رسم کنیم، یک دایره با شعاع تشکیل میشود که در جهت عقربههای ساعت با سرعت زاویهای میچرخد. شکل زیر این مسئله را نشان میدهد.
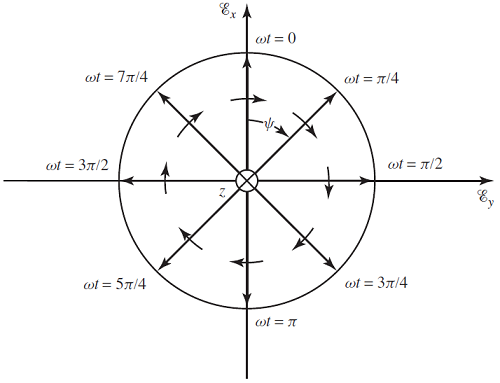
در این حالت گفته میشود که موج، پلاریزاسیون دایروی راستگرد دارد. ذکر این نکته ضروری است که چرخش از پشت موج و از جهت انتشار آن باید در نظر گرفته شود. در این مثال، موج در جهت منتشر میشود، بنابراین نقطه مشاهده از مبدأ و به سمت داخل صفحه خواهد بود. میتوان بردار میدان الکتریکی لحظهای را به صورت زیر نوشت:
توجه کنید که در این حالت بین دو مولفه متعامد در بردار میدان الکتریکی، اختلاف فاز وجود دارد.
پس میتوان گفت که یک موج پلاریزاسیون دایروی راستگرد دارد اگر و فقط اگر دو مولفه متعامد پلاریزه شده به صورت خطی آن دامنههای یکسان و اختلاف فازی معادل داشته باشند. جهت چرخش میدان بر این اساس مشاهده میشود که موج از ناظر در حال دور شدن است.
پلاریزاسیون دایروی چپگرد
اگر بردار میدان الکتریکی چرخشی در جهت خلاف عقربههای ساعت داشته باشد، پلاریزاسیون را چپگرد مینامند. برای نشان دادن این موضوع فرض کنید:
بنابراین
مکان هندسی دامنه میدان عبارت است از:
زاویه نیز به وسیله رابطه زیر داده میشود:
مکان هندسی بردار میدان، دایرهای به شعاع است که در خلاف حرکت عقربههای ساعت با فرکانس زاویهای میچرخد. شکل زیر این مسئله را نشان میدهد.
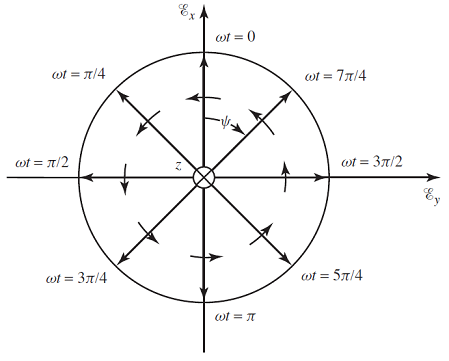
در این حالت، گفته میشود که موج پلاریزاسیون دایروی چپگرد دارد. بردار لحظهای میدان الکتریکی لحظهای به صورت زیر نوشته میشود:
بنابراین در حالت کلی میتوان گفت که یک موج پلاریزاسیون دایروی چپگرد دارد اگر و فقط اگر دو مولفه متعامد آن دامنههای یکسان و اختلاف فاز این دو مولفه معادل ضرایب فرد باشد.
شرایط لازم و کافی برای وجود پلاریزاسیون دایروی به صورت زیر است:
- میدان باید دو مولفه متعامد داشته باشد.
- دو مولفه باید دامنه یکسان داشته باشند.
- اختلاف فاز زمانی دو مولفه باید ضرایب فرد باشد.
بیضی پلاریزاسیون
یک موج تکفام پلاریزه شده به صورت خالص را در نظر بگیرید.
اگر بردار میدان الکتریکی برای یک دوره تناوب از نوسان رسم شود، در حالت کلی یک بیضی حاصل میشود که مربط به پلاریزاسیون بیضوی است. شکل زیر، این مسئله را نشان میدهد.
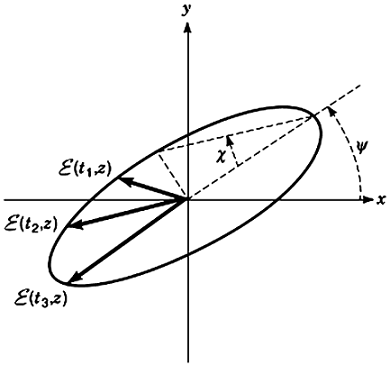
یادآوری این نکته ضروری است که پلاریزاسیونهای خطی و دایروی، حالتهای خاصی از پلاریزاسیون بیضوی هستند.
بنابراین حالت پلاریزاسیون را میتوان نسبت به پارامترهای هندسی بیضی و جهت آن تعریف کرد. منظور از جهت بیضی، چرخش میدان در جهت عقربههای ساعت یا در خلاف جهت عقربههای ساعت است. «زاویه جهتگیری» (Orientation Angle) با نماد نشان داده میشود. زاویه جهتگیری به صورت زاویه بین محور اصلی بیضی و محور x تعریف میشود. نسبت طول محور اصلی بیضی به محور فرعی آن، «بیضیت» (Ellipticity) یا «نسبت محوری» (Axial Ratio) نام دارد. بنابراین نسبت محوری برای یک بیضی به صورت زیر خواهد بود:
پارامتر بیضیت یک پارامتر جایگزین برای «دوری از مرکز» (Eccentricity) برای بیضی است. گریز از مرکز یا دوری از مرکز برای یک بیضی به صورت زیر تعریف میشود:
«زاویه گریز از مرکز» (Ellipticity Angle) برای یک بیضی نیز به صورت زیر تعریف میشود:
همچنین زاویه X برای تعریف عرض جغرافیایی (زاویه از خط استوا) حالت پلاریزاسیون نیز استفاده میشود. بیضیت یا در حالت خاصی که پلاریزاسیون خطی داریم، برابر بینهایت () و برای پلاریزاسیون دایروی برابر یک () است.
بنابراین یک بیضی را میتوان با جفت پارامترهای () یا () تعریف کرد.
بردار جونز
حالت پلاریزاسیون را میتوان به وسیله دامنه و فاز نوسانها برای دو مولفه بردار میدان الکتریکی در صفحه پلاریزاسیون نیز نوشت. اطلاعات دامنه و فاز را به صورت یک بردار مختلط دو بعدی نوشته میشود. این بردار، بردار جونز نام دارد و به صورت زیر تعریف میشود:
در این معادله، و دامنه موج در دو مولفه بردار میدان الکتریکی و و فاز بردار را نشان میدهند. حاصلضرب یک بردار جونز و یک عدد مختلط با قدر مطلق واحد، بردار جونزی متفاوت اما با حالت پلاریزاسیون یکسان را به دست میدهد. در این حالت، میدان الکتریکی فیزیکی به عنوان بخش حقیقی بردار جونز تغییر میکند، اما حالت پلاریزاسیون مستقل از «فاز مطلق» (Absolute Phase) بردار است. حتما لازم نیست که بردار پایه نشاندهنده بردار جونز، حالت پلاریزاسیون خطی داشته باشد (یعنی حقیقی باشد). در حالت کلی، هر جفت بردار متعامد قابل استفاده است. حاصلضرب داخلی یک جفت بردار متعامد، برابر صفر است. برای مثال پلاریزاسیونهای دایروی راستگرد و چپگرد را در نظر بگیرید. این دو بردار متعامد هستند. از جمله مثالهای این جفت بردار، میتوان محیط دوشکستی یا انکسار مضاعف را نام برد.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس مهندسی برق
- آموزش الکترومغناطیس مهندسی (مرور و حل تست کنکور ارشد)
- امواج الکترومغناطیسی — از صفر تا صد
- میدان مغناطیسی جریان — از صفر تا صد
- مغناطیس چیست؟ — به زبان ساده
^^












باسلام و احترام
قسمت پلارازیسون خطی به صورت کد وار نشان داده میشود
با سلام خدمت شما؛
فرمولهای بخش پلاریزاسیون خطی بررسی شد و اصلاحات لازم اعمال شد. منظور از [] Re، بخش حقیقی عبارت است که پس از تساوی، بخش حقیقی عبارت موردنظر بهدرستی نوشته شده است.
از همراهی شما با مجله فرادرس سپاسگزاریم.
آیا مجموع دو موج با پلاریزاسیون دایروی راسگرد (چپگرد) باز هم دایروی راستگرد (چپگرد) می باشد؟ درصورت مثبت بودن جواب، تعریف اول از شرایط لازم وکافی برای پلاریزاسیون دایروی که بیان می دارد :۱- میدان باید دو مولفه متعامد با پلاریزاسیون خطی داشته باشد. بایستی به صورت زیر تغییر کند: میدان باید دو مولفه متعامد داشته باشد.
لطفاً پیرامون این موضوع توضیح دهید.
چقدر سخت، من که چیزی نفهمیدم
با سلام؛
متن ویرایش شد،
با تشکر از همراهی شما با مجله فرادرس
آیا مجموع دو موج با پلاریزاسیون دایروی راسگرد (چپگرد) باز هم دایروی راستگرد (چپگرد) می باشد؟ درصورت مثبت بودن جواب، تعریف اول از شرایط لازم وکافی برای پلاریزاسیون دایروی که بیان می دارد :1- میدان باید دو مولفه متعامد با پلاریزاسیون خطی داشته باشد. بایستی به صورت زیر تغییر کند: میدان باید دو مولفه متعامد داشته باشد.
لطفاً پیرامون این موضوع توضیح دهید.
چقدر عالی هست مقاله های فرادرس……ممنون بابت تمامی زحماتتون
خیلی عالی…